Comment exploiter $(x,y)\mapsto (x+y,x-y)$ avec des collégiens ?

stfj
stfj
Modifié (October 2022) dans Pédagogie, enseignement, orientation
$S:\mathbb{Z}^2 \to \mathbb{Z}^2, (x,y) \mapsto (x+y,x-y)$ peut être introduite à des collégiens, même au début du collège, via des repères cartésiens (en parlant des "noeuds du quadrillage" et en examinant des exemples tels que $(3,2)\mapsto (5,1)$. D'un point de vue théorique, c'est intéressant puisqu'il s'agit de la restriction aux entiers de Gauss d'une similitude indirecte. Mais là n'est pas la question ici.
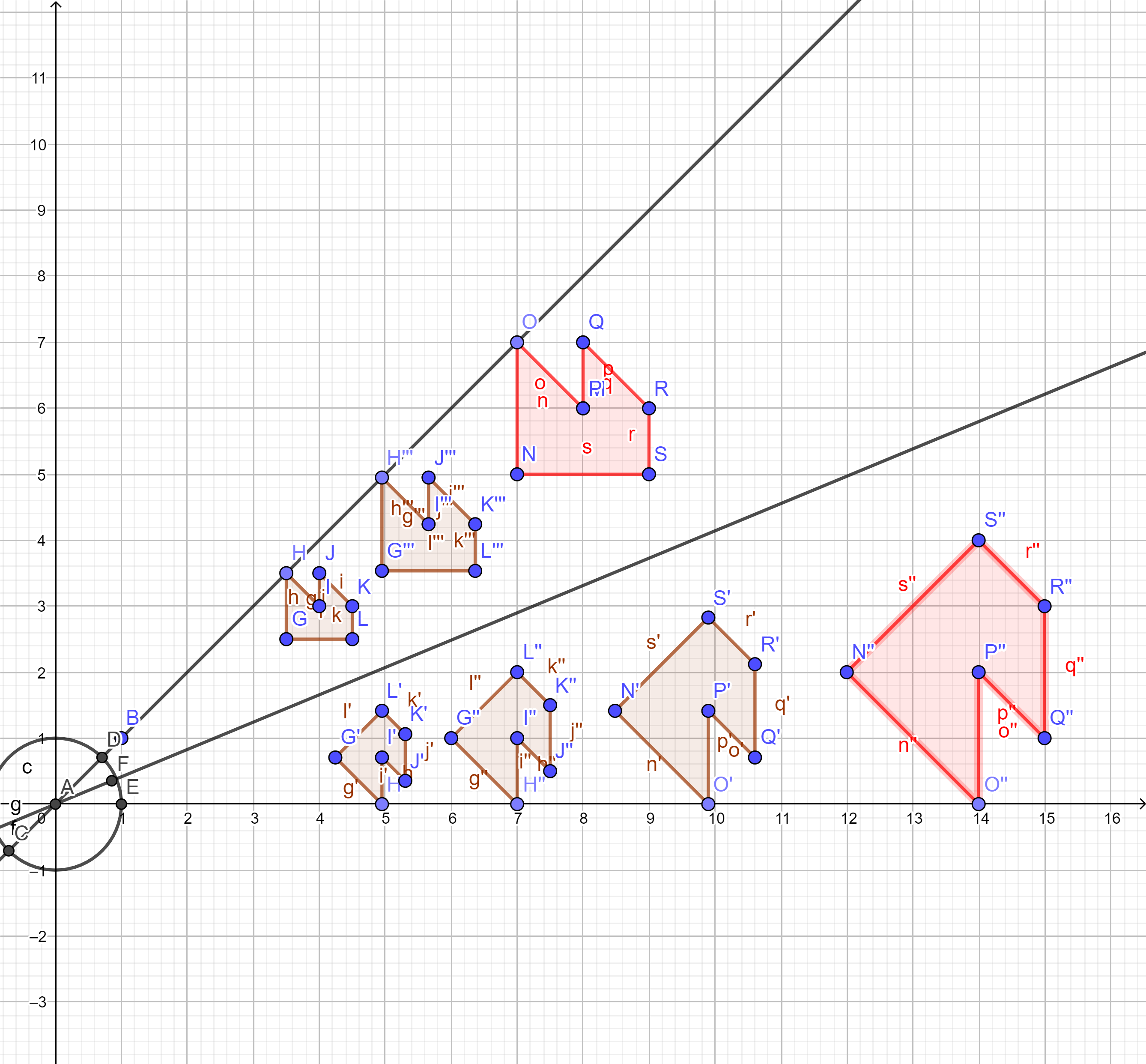
A travers des dessins de l'image de figures non symétriques simples du plan $xOy$ (bateaux, petite usine,...), on peut leur expliquer que c'est la composée d'une symétrie d'axe $(Oz)$ telle que $\widehat{xOz}=22,5°$ et d'un agrandissement de rapport $r$. Comme la composée $S^2$ s'avère être une homothétie de rapport $2$, ils peuvent avoir l'intuition que $r^2=2$. 
Soit $s$ la symétrie d'axe $(Oz)$ : on a $S=sh=hs$ donc $S^2=shsh=hssh=h^2$. 
En algèbre linéaire, tout est simple. Mais des élèves en début de collège ne disposent évidemment pas encore de ces outils puissants. Je trouverais néanmoins regrettable de ne pas exploiter à fond avec leurs connaissances une similitude aussi simple. Alors que faire ? Si vous avez des idées, je suis preneur.
Cordialement.


Réponses

  • Dom
    Dom
    Modifié (October 2022)
    L’homothétie est au programme. 
    La géométrie n’est quasiment plus que du « on voit que ». 
    Les fonctions sont au programme (bon… trivialement… et sans technicité… et je ne sais pas si avec deux variables ça reste dans le cadre…) Il paraît donc exploitable de proposer de placer des points dans un quadrillage (un repère…) puis d’appliquer cette fonction (à présenter pour que ce soit compréhensible : deux variables, ça passe mais peut-être faut-il surtout faire des exemples au lieu de théoriser le truc…). 
    Enfin, entre la figure originale et la figure finale, demander de trouver la transformation (sans justifier à l’écrit). 
    Je vais communiquer ça à des profs, tiens 😀
    C'est à la fois une récréation (ce n’est pas péjoratif !) et pertinent. 
  • stfj
    stfj
    @Dom :  tu as évidemment raison, il faut rester pour de jeunes élèves avec des exemples tels que $(\color{green} 3,\color{Red} 1)\color{Blue} \to (\color{Green} 3+\color{Red} 1,\color{Green} 3-\color{Red} 1)$. A propos, comme quoi il faut toujours poser des questions pour trouver la réponse, j'ai trouvé comment montrer que c'est une homothétie de rapport 2 : $(3,1)\to (3+1,3-1) \to (3+1+3-1,3+1-(3-1))=2(3,1)$ :)
  • Dom
    Dom
    Modifié (October 2022)
    Ton fil m’apprend cela : on a une homothétie, j’allais dire, « par surprise ». Je suis inculte dans bien divers domaines 😀

    Édit : par contre les valeurs propres sont opposées… quand on diagonalise on n’obtient pas une « homothétie au sens matriciel ». Dis-je des bêtises ?

    Édit : j’ai parlé trop vite, tu avais tout dit, une homothétie mais composée avec une symétrie axiale. 
  • Math Coss
    Math Coss
    Modifié (October 2022)
    En première année post-bac, on regardera l'image de la base canonique et on verra deux vecteurs orthogonaux. Alors on dira qu'en d'autres temps on aurait reconnu une similitude. On écrira tout de même la matrice de passage et son inverse.
    Ou bien on cherchera l'expression en complexes.
  • Dom
    Dom
    J’allais le dire. C’est « similitude (indirecte) » qui est le terme idoine. 
  • bisam
    bisam
    Il me semble qu'on peut encore parler du point $M$ de coordonnées $(x,y)$, de son image $M'$ (par une application à laquelle on n'est pas obligé de donner un nom) de coordonnées $(x',y')=(x+y,x-y)$, et je pense qu'il y aura une partie non négligeable des élèves qui arrivera à calculer que l'image $M''$ de $M'$ a pour coordonnées $(x'',y'')=(x'+y',x'-y')=((x+y)+(x-y),(x+y)-(x-y))=(2x,2y)$. Ce ne sont quand même que des additions et des soustractions ! On n'a même pas besoin de parler de vecteurs !
  • Dom
    Dom
    1) Le concept est simple mais son écriture posera évidemment un problème.
    Par exemple, écrire des calculs dans des coordonnées, ça va coincer pour plus de la majorité. Je ne dis pas que c’est difficile, je dis que ça va coincer. J’enfonce le clou : même une égalité entre deux couples, ça surprendra plus de la majorité des élèves. 
    2) La majorité des élèves se plantent pour réduire cette somme et cette différence. C’est le calcul littéral qui foire, c’est un autre sujet. 
  • rebellin
    rebellin
    Cette transformation a aussi des propriétés algébriques intéressantes : on peut faire chercher des antécédents (résolution d'un système dans un cas simple) et remarquer que ce n'est pas surjectif $\mathbb{Z}^2\to\mathbb{Z}^2$ (commencer par observer, sur des exemples, que les termes du couple image ont la même parité). On peut également chercher la transformation inverse, ce qui rejoint le message de @bisam
  • stfj
    stfj
    @rebellin : merci, je n'avais pas pensé à cela. Par exemple $(15,2)$ n'a pas d'antécédent dans $\mathbb{Z}^2$.  Et ensuite $\begin{Bmatrix} x'=\frac{x+y}2  \\ y'=\frac{x-y}2 \end{Bmatrix}$
  • stfj
    stfj
    Pour ceux que cela intéresse, pour gagner du temps et obtenir rapidement l'axe de symétrie de $22,5°$, on peut tracer la droite $(OA)$, où $O$ désigne l'origine du repère et $A=(17,7)$ : en effet, $\arctan\frac{7}{17}\approx 22,38°$
  • nicolas.patrois
    nicolas.patrois
    Application : un peu de cryptographie (c’est en gros celle de Hill) où on chiffre les caractères par paires.
    Algebraic symbols are used when you do not know what you are talking about.
            -- Schnoebelen, Philippe
Connectez-vous ou Inscrivez-vous pour répondre.

Bonjour!

Pour participer au forum, cliquer sur l'un des boutons :

Connexion S'inscrire

Catégories

In this Discussion

Qui est en ligne 5

GG +4 Invités