Mathémagie
Bonjour à tous
J'ouvre cette discussion pour "recenser" des tours de magie qui parlent de mathématiques ou qui reposent sur des principes mathématiques. Je fais un peu de magie (en amateur pour passer le temps) et je n'ai pas réussi à trouver énormément de tours de magie en rapport avec les mathématiques. Je fais donc appel à vous pour élargir cette liste le plus possible.
Je propose de ne pas révéler les "trucs" pour les produits que vous connaitriez et qui seraient commercialisés (juste mentionner les référence des produits). Pour les tours qui ne seraient a priori pas commercialisés, je vous laisse le choix de révéler directement les secrets ou pas. Vous pouvez aussi décrire les effets pour laisser les participants à cette discussion chercher un peu et proposer des idées avant de révéler les trucs ou de dire si un participant a trouvé (dans ce cas, essayez si possible de décrire assez précisément les effets sans omettre de détail important que l'on verrait lors d'une vraie performance et qui pourrait donner des idées sur la façon dont le tour est réalisé).
Voici quelques "produits" que je connais.
Deux livres chez ellipses:
Un troisième que je viens de découvrir en cherchant (mais je ne sais pas s'il ne s'agit pas d'une nouvelle version des premiers ouvrages):
4) Les effets de calculateurs "prodiges" (ou l'on donne l'illusion de savoir faire des opérations monstrueuses plus rapidement qu'un spectateur munit d'une calculatrice). Je n'ai pas de référence précise en tête ; si vous avez des références ou connaissez quelques exemples de tours dans le genre je suis preneur (je ne m'intéresse évidemment pas à certains mathématiciens qui sont effectivement calculateur prodiges et qui pourraient faire le même effet en faisant vraiment les calculs de tête! :-D ).
Trois autres livres:
(Je précise que je ne suis pas la personne sur la vidéo).
Voilà ce que j'ai réussi à lister pour le moment. On pourra également recenser ici des tours "automatiques", comme des tours de cartes qui ne reposent sur aucune grosse manipulation et qui "marchent tout le temps" (mais du moment que ceux-ci reposent sur un principe pouvant être relié aux mathématiques).
Je vous remercie d'avance pour votre aide !
Réponses
-
Bonsoir
ci-joint un sujet que j'ai donné il y a quelques années, avec des morceaux de Python dedans.
-
Bonsoir @adrien2019,
Connais-tu celui-ci ? Il est excellent ! https://www.amazon.fr/Magical-Mathematics-Revealing-Secrets-behind/dp/0691151644
Essaie également le mot clé "math" sur conjuring archive, tu trouveras plein de références !
https://www.conjuringarchive.com/list/search?keyword=math
-
@Philippe Malot non je ne connaissais pas ce livre! J'ai vu qu'il cite Persi Diaconis, mathématicien, ex-magicien (je n'avais pas pensé à le citer plus haut) et qui a fait un super travail sur les mélanges de cartes (j'aurais bien voulu travailler dessus mais à chaque fois que j'avais une idée de truc à chercher je me suis rendu compte qu'il avait déjà étudié la question ^^). Je connaissais de nom Ron Graham comme mathématicien, mais je ne savais pas qu'il était aussi jongleur! Merci également pour le lien sur "conjuring archive" (je ne connaissais pas ce site).@jmf merci pour ce sujet! Ça me rappelle un tour de cartes que j'avais appris au lycée. Je vous donne une description de l'effet et je vous laisse chercher un peu avant éventuellement de donner la solution.Effet: le magicien sort un jeu de cartes, l'éventail (faces en bas) et fait choisir une carte au spectateur. Le spectateur remet ensuite sa carte face en bas sur le dessus du paquet, et le magicien l'invite à couper le jeu autant de fois qu'il le souhaite (par "couper" j'entends "séparer le jeu en deux puis compléter la coupe"; pas de coupe en 3 paquets par exemple). Le magicien l'invite ensuite à retourner le jeu face en l'air sur la table et à refaire encore quelques coupes. Au bout d'un moment, le magicien l'arrête, lui dit de remettre le jeu face en bas, se concentre, et, malgré toutes ces coupes, arrive à dire au spectateur exactement en quelle position sa carte se trouve.Je vous laisse chercher un peu!Un autre "tour" qui vient de me revenir, et qui devrait faire buguer tous les topologistes parmi vous ^^ :
 (celui-là se vend donc je ne dévoilerai pas le truc ici).
(celui-là se vend donc je ne dévoilerai pas le truc ici). -
À propos de « rond-carré » il existe une illusion où l’objet plutôt carré est reflété en un objet plutôt rond dans un miroir.
-
On arrive à comprendre facilement le principe, mais j'avoue que j'aurais du mal à modéliser cela rigoureusement. Quelqu'un aurait-il une idée sur une formalisation mathématique du principe derrière ce tour?
-
Bonjour,
Extra ce "rond-carré" ! Pour faire réfléchir les élèves c'est top. Sous la vidéo postée par Dom il y a un pdf pour construire l'objet, mais pour un collégien la courbe utilisée apparaîtra bien énigmatique. Ce toit d'un garage est plus accessible. Ci-dessous, un patron pour le fabriquer (extrait du livre Joy of Ambiguous Solids de Kokichi Sugihara, Sugi Lab., Inc. 2015)
-
Il y a un trompe-l'oeil assez connu, c'est le YES/NO de Markus Raetz. En voici une version française. Â propos de cette oeuvre, je me demandais si on pouvait fabriquer (et comment ?) une sculpture qui, vue sous un angle donne une lettre de l'alphabet, et vue sous un autre angle donne une autre lettre. Et cela pour n'importe quelles lettres.
Et aussi : quelles sont les formes pour lesquelles cela est impossible ? -
On prend un cube (de bois) on "enlève" un G dans une direction, un E dans une autre et un B (avec quelques précautions) dans la troisième, on obtient un objet qui, placé pas trop loin d'un angle d'une pièce et avec 3 lampes de poche, on obtient les 3 lettres.Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
@Ludwig super ce OUI/NON!Autre tour qui me revient: on demande au spectateur de penser à un chiffre, on lui fait faire une série d'opérations, et on devine le résultat. Souvent ça commence par quelque chose comme "Pensez à un nombre, multipliez-le par 9, divisez ensuite par le nombre de départ, et ce qu'on veut après pour brouiller les pistes...". C'est bête mais étonnement ça marche bien sur les gens (encore faut-il qu'ils n'aient pas pensé à 0).
-
Bonsoir,
quelques visions magico-mathématiques de Martin Gardner (extrait de ma bibliothèque personnelle).
-
@df très joli !Je reviens sur cette discussion pour ajouter d'autres choses auxquelles j'ai repensé récemment. Il y a les tours de "carrée magiques", où un spectateur donne un nombre et le magicien rempli en un temps record un carré magique ayant pour sommes ce nombre (des formules simples permettent évidemment de remplir le carré très rapidement quel que soit le nombre donné par le spectateur).Une autre vidéo à laquelle j'ai repensé :Je ne sais pas si l'on peut parler de "tour de magie" puisque ça n'est pas présenté comme tel, mais en même temps les carrés magiques qu'on remplit de tête sont aussi des effets que le magicien peut présenter comme une démonstration de capacités mentales exceptionnelles plutôt que comme un tour de magie (bien que ça relève plus d'un "truc" que de d'une prouesse mentale).Un autre principe dont je me suis rappelé: le mathematical three card monte de Bob Hummer. Voici une vidéo d'une adaptation de ce principe :Je ne sais pas si l'explication du principe est disponible en ligne (je n'ai pas fouillé, j'ai juste cherché tapé le nom du tour pour retrouver le nom de l'auteur), donc je ne donnerai pas l'explication ici (mais c'est sans doute trouvable en ligne si ça vous intéresse).Je me demandais aussi s'il était possible d'utiliser le paradoxe de Simpson (ou d'autres paradoxes) pour construire des tours de magie. Quelqu'un sait-il s'il y a des tours qui reposent là-dessus ou quelqu'un a-t-il une idée pour en faire un tour ?Merci pour les réponses que vous avez déjà apportées !
-
Le (prétendu) théorème de Rasmussen : un accident nucléaire ne se produit que tous les 35000 ans(Référence : La vérité sur le nucléaire de Corinne Lepage aux éditions Albin Michel (juin 2011)) est dans la catégorie magie noire et propagande du lobby nucléaire !Les mathématiques ne sont pas vraies, elles sont commodes.Henri Poincaré
-
Pour ce tour, on a $24$ cartes bien mélangées. Dans une audience, un premier participant choisit une carte qu’il montre à tout le monde sauf au magicien; puis il remet la carte dans le paquet: dans l’exemple attaché, il s’agit de l’$\textbf{as de pique}$. Un deuxième participant choisit un nombre entre $1$ et $24$ (disons $18$) et le révèle à tout le monde.
Après avoir mélangé le paquet, le magicien distribue les cartes en $2$ piles de $12$ cartes et demande au premier participant de lui désigner la pile contenant la carte choisie. Dans l’exemple, c’est la deuxième pile qui contient l’as de pique.
Le magicien récupère soigneusement les deux piles et reconsolide le paquet de $24$ cartes. Cette fois, il distribue alternativement les $24$ cartes en $3$ piles de $8$ cartes chacune. Puis, à nouveau, il demande au premier participant de lui désigner la pile contenant la carte choisie. Dans l’exemple, il s’agit de la première pile (celle qui contient l’as de pique).
Le magicien récupère les piles et distribue alternativement les $24$ cartes en $4$ piles de $6$ cartes. Une dernière fois, le premier participant indique au magicien la pile contenant la carte choisie. Le magicien rassemble les piles, l’une après l’autre. Une fois son paquet reconstitué, il retourne les cartes une par une, en les comptant à voix haute. La $\textbf{dix-huitième carte}$ (le nombre choisi par le deuxième participant) est l’$\textbf{as de pique}$.

-


-
Le tour est peut-être plus parlant si on le fait avec $27=3^3$ cartes.
Le premier participant choisit sa carte et le second, un nombre $n$ entre $1$ et $27$.
Le magicien effectue alors $3$ distributions alternées consistant chacune en $3$ piles de $9$ cartes. Après la troisième distribution, la $n$-ième carte retournée est toujours la carte choisie. -
Bonsoir,Merci pour la description de ce tour de magie dont l'exposé détaillé de ses ressorts mathématiques, bien que relevant d'une arithmétique élémentaire, s'avère moins facile qu'il n'y parait.Il y a donc un "magicien" qui dispose d'un jeu de $N = \displaystyle \prod_{i=1}^k n_i$ cartes qu'il scinde successivement en $n_1, n_2, \dots, n_k $ piles selon la procédure décrite et qui, au terme de ses manipulations, doit faire en sorte que la carte choisie par un spectateur se retrouve en $A\text{-ième} $ position, où $A\in [\![1;N]\!] $ est le nombre choisi par un autre spectateur.Lorsqu'il prend connaissance du nombre $A$, il effectue un calcul mental qui consiste à déterminer le $k-\text{uplet }\: (x_1,x_2, \dots x_k)$ défini par la proposition suivante: Notons:$\:\: \forall i \in [\![1;k+1]\!], \quad N_i :=\displaystyle \prod_{j=1} ^{i-1} n_j , \qquad( N_1=1, \:\: N_{k+1} =N).\quad$$$\boxed{ \exists ! \:(x_1,x_2,\dots x_k) \in \N^k \text{ tel que }\: A -1= \displaystyle \sum _{i=1}^k x_i N_i, \quad 0\leqslant x_i<n_i.}$$Les $\:x_1 ,x_2,\dots x_k$ sont définis par récurrence par: $\quad A-1 \equiv x_1 \mod n_1 , \quad 0\leqslant x_1<n_1, \qquad \dfrac 1 {N_{i+1}}\left( A-1 - \displaystyle \sum _{j=1}^{i} x_jN_j \right) \equiv x_{i+1}\mod n_{i+1} , \quad 0\leqslant x_{i+1}<n_{i+1} \square $Il opère alors le $i\text{-ième}$ regroupement des piles, en prenant soin de placer celle qui contient la carte cherchée en $\boxed{\text {position numéro } x_i}$ parmi les $n_i$ piles, ces positions étant "numérotées" de $0$ à $n_i -1.$En effet, dans ces conditions, pour tout $j\in [\![1;k]\!]$, au terme du $j\text{-ième}$ "partage-regroupement", la position de la carte "mystère" dans l'ensemble des $N$ cartes appartient à l'intervalle $\mathcal I_j=\left(\dfrac {N}{N_{j+1}}\displaystyle \sum_{i=1}^j x_iN_i \right) \: + \: [\![1\: ;\: \dfrac {N}{N_{j+1}} ]\!].\qquad $ Ainsi: $\:\:\mathcal I_k =\{A\}\:\square$Dans la situation présentée avec $24$ cartes et $A=18$:$ N_1 =1, \:\: N_2 = 2, \:\: N_3 =6, \:\:x_1 =1, \:\: x_2 =2, \:\: x_3 =2, \quad \mathcal I_1 = [\![13 ; 24]\!], \quad \mathcal I_2 = [\![ 21 ; 24 ]\!], \quad \mathcal I_3 = \{18\}.$Il place donc la pile désignée en dernière position à l'issue du premier partage et du second partage, en troisième position à l'issue du dernier.
-
Comme l’a bien dit LOU16, la clé du tour est dans la manière de positionner, après chaque distribution, la pile contenant la carte choisie par rapport aux autres piles.
Bien sûr, une fois que la bonne position est déterminée (par la procédure adéquate), on peut placer les autres piles à sa guise. -
Un tour de magie que j'ai transmis à ma petite fille Dolorès Cidrolin (huit ans).On choisit quatre bandelettes parmi les douze ($12\times11\times10\times9$ façons). Dolorès peut donner instantanément le total des quatre nombres de quatre chiffres obtenus. Par exemple si on choisit les quatre bandelettes de gauche, dans l'ordre de la photographie, l'addition est : $6788+9779+5507+3431$. Pas le temps de dire ouf que déjà la petite a donné la réponse. Comment fait-elle ?

-
Pas du tout Math Coss !!!Les mathématiques de ce tour sont hors de portée d'un bac-9, cependant elle répondrait plus vite que Giacomo Inaudi.
-
Sauf erreur de ma part, sur chaque bandelette, la somme des nombres sur les 1ère, 2ème et 4 ligne fait toujours $18$.Il suffit donc de lire le nombre écrit sur la 3ème ligne, en enlevant $2$ au chiffre de droite et en le mettant ce $2$ devant le tout.Dans l'exemple évoqué, on lit $5507$, on coupe le $7$ en $2+5$ et on annonce $25505$ comme total.
-
Bravo bisam !Ce tour est effectivement basé sur la remarque : $18\times1111=19998=20000-2$.
-
@toutlemonde merci pour vos réponses! De jolie principes en effet!Un nouveau tour dont je viens de me souvenir:En gros pour la partie "mathématiques", ça va de 0:27 à 1:50; en gros, il a fait choisir une carte, et il arrive à la faire apparaitre imprimée sur un jeu de cartes. Je ne donnerai pas le truc de ce tour car il est commercialisé, mais je trouve que le raisonnement derrière (je dirai juste "le découpage des choix possibles" pour rester flou) est une façon de raisonner très mathématique; c'est pour ça que j'ai mis ce tour ici. En espérant que ça vous amuse et que ça vous fasse réfléchir un peu!

-
@Philippe Malot j'ai acheté le livre que vous m'avez conseillé. Je ne l'ai pas terminé (mais j'en ai lu une bonne partie)... il est en effet super ! Merci pour cette référence !@Cidrolin je suis récemment tombé sur ce tour : https://www.marchanddetrucs.com/magasin-de-magie/scene-salon/the-human-abacus-5906.html
Il s'agit sans toute en partie du tour que vous avez mentionné . Je dis "en partie" car dans le lien que j'ai donné, ils vendent aussi un "booktest" sur pi (un autre que celui dans le premier message que j'ai posté dans cette discussion).Deux autres références que j'ai trouvées depuis mon dernier message.Un tour pour faire des carrés magiques facilement (je donne une vidéo de critique car il développe pas mal ce que fait le tour):
. Je dis "en partie" car dans le lien que j'ai donné, ils vendent aussi un "booktest" sur pi (un autre que celui dans le premier message que j'ai posté dans cette discussion).Deux autres références que j'ai trouvées depuis mon dernier message.Un tour pour faire des carrés magiques facilement (je donne une vidéo de critique car il développe pas mal ce que fait le tour): Dans le livre suivant, il y a une grosse partie sur l'arithmétique (de ce que j'ai compris: entre autres sur les calculs rapides de carrées, de cubes, de racines, de dates, d'autres choses sur le carré magique): https://www.magicdream.fr/livre-the-thirteen-steps-to-mentalism-fr-corinda.htmlJe n'ai pas ce livre donc je donne une description de ce que j'ai entendu.Merci pour les réponses que vous avez déjà données, et n'hésitez pas si vous avez de nouvelles références!
Dans le livre suivant, il y a une grosse partie sur l'arithmétique (de ce que j'ai compris: entre autres sur les calculs rapides de carrées, de cubes, de racines, de dates, d'autres choses sur le carré magique): https://www.magicdream.fr/livre-the-thirteen-steps-to-mentalism-fr-corinda.htmlJe n'ai pas ce livre donc je donne une description de ce que j'ai entendu.Merci pour les réponses que vous avez déjà données, et n'hésitez pas si vous avez de nouvelles références! -
En tant que passionné de magie dans mon enfance, je vous remercie pour ce fil passionnant et qui permet en prime de trouver des accroches en société pour rendre les maths "charmantes" et parler de ce qu'on aime à des "profanes", souvent tristement bloqués psychologiquement par les maths.
-
Bonjour,je ne peux m'empêcher de vous recommander vivement les livres de Dominique Souder pour les personnes intéressées par ce merveilleux sujet !Ils sont géniaux ! Voici un lien vers le site : https://club-math-and-magie-souder.jimdosite.com/J'ai acheté plusieurs de ses livres notamment ceux de niveau collège (car pour le moment j'enseigne en collège).J'en fais un tous les ans durant la toute première heure de cours et dans toutes mes classes (même en 4ème : ça permet de les mettre en confiance sur quelque chose de très simple) sauf en 3ème (programme plus chargé et année du brevet) pour commencer tranquillement l'année, après avoir fait un bon topo sur les règles de vie et les consignes.Le but est de "prédire" le résultat d'une addition constituée de $5$ nombres de $4$ chiffres :1) J'écris une prédiction sur un bout de papier comme par exemple : $26$ $465$ et je mets le bout de papier refermé sur le bureau. Je dis à un élève assis devant de surveiller ma prédiction : pour vérifier qu'il n'y a pas de triche hahaha !2) J'écris au tableau le nombre $6$ $467$ .3) Un élève me donne un nombre de $4$ chiffres pas trop "particulier" (surtout pas $9$ $999$ par exemple) et je fais du théâtre pour écrire le suivant (le complément à $9$ $999$ en réalité).4) On répète une fois l'étape $3$.5) Les élèves posent l'addition dans le cahier d'exercices. Je passe les aider et les valoriser.Ceux qui finissent rapidement essaient de comprendre quelle est l'astuce.6) J'envoie un élève corriger au tableau, on commente sa correction et on explique enfin tous ensemble comment le tour fonctionne !Voilà


-
-
Ah aussi ! J'avais sous la main ce site : http://therese.eveilleau.pagesperso-orange.fr/ depuis pas mal de temps !!!Le tour de télépathie (dans l'onglet "magie" en haut) est très sympa (il repose sur la table de $9$, c'est une belle preuve à faire avec une classe de 3ème pour les initier à ce genre de preuve d'arithmétique qui reste un peu au programme de 3ème, de manière très raisonnable et très élémentaire).Malheureusement, ce tour nécessite le téléchargement d'un fichier : on ne peut plus le faire directement en ligne en cliquant sur la boule du site. Cela dit, on peut se servir du tableau et le faire avec des élèves quand même donc ce n'est pas vraiment problématique ^^
-
@Riemann_lapins_cretins ravi que ce fil vous plaise !@NicoLeProf joli site ! Et merci pour la référence des livres, je la note !@JLapin supère énigme ! Je ne connaissait pas !Je viens de me souvenir qu'il existe également pas mal de tours autour du Rubik's Cube. Je recommande le tour suivant à ceux qui s'intéressent à cet objet (je mets la critique qui détaille ce que le tour contient) :Il contient entre autres une vidéo très détaillée de la résolution du Rubik's cube, bien meilleure que la plupart des tutoriels internet, et comme c'est une vidéo, on peut voir les manipulations à effectuer plus clairement que sur un livre. Rien que pour cette première vidéo, je recommande ce tour à tous ceux qui voudraient apprendre à résoudre un Rubik's cube. Il y a également une seconde vidéo avec plusieurs tours expliqués (une fois qu'on maîtrise la résolution du cube).Il y a également d'autres tours avec des Rubik's cube. Je cite notamment Henry Harrius (qui est un peu la référence dans le domaine des cubes): https://hhpresents.com/collections/cube-seriesLes tours d'Henry Harrius reposent plus sur des "gimmicks" que sur des algorithmes de résolution (même s'il en faut à peu près pour tous les tours de cubes), mais je les laisse quand même ici car c'est en rapport avec l'objet "mathématique" qu'est le Rubik's cube.
-
Aie aie aie!!! Comment ai-je pu faire un post sur les mathémagie sans évoquer le puzzle de Sherlock Holmes !!!Je n'aime pas tellement la présentation que j'ai partagée. Bernard Bilis en a fait une (que je trouve meilleure) au Plus Grand Cabaret du monde. Je n'ai pas retrouvé la vidéo ; si quelqu'un arrive à la retrouver, peut-il la partager ?
-
Ca fait vraiment partie d'un spectacle ce tour du carré de chocolat manquant ?

-

Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
@JLapin et @nicolas.patrois Attention! Dans ma vidéo, la seule vraie partie magique est qu'à la fin, le puzzle re-rentre exactement dans le cadre, comme au début! (Ce n'est pas tellement le fait de refaire un rectangle avec des pièces en plus: cela repose juste sur une conception adéquat des pièces du puzzle). Ce n'est pas le cas dans l'exemple des carrés de chocolat...

-
Si, la tablette de chocolat pourrait rentrer dans le même cadre de 4*6 à un carré de chocolat près.
-
@JLapin
 oui mais elle ne pourrait pas remplir entièrement le cadre (sans laisser de vides)... C'est le cas du puzzle au début ET à la fin du tour.
oui mais elle ne pourrait pas remplir entièrement le cadre (sans laisser de vides)... C'est le cas du puzzle au début ET à la fin du tour.
-
Dans la tablette de chocolat, le rectangle initial est $6\times4$ et, après suppression d'un carré, il est toujours de $6\times4$ !Sauf erreur, il s'agit du même truc, des pentes rationnelles proches les unes des autres qui laissent un trou dans la version finale : l'aire du trou est $1$ mais le trou est si allongé qu'on ne le voit pas vraiment, ou plutôt qu'on l'attribue à l'imprécision de la construction concrète (bois ou chocolat). Je connais une version de cette histoire depuis ma tendre enfance, ce qui commence à représenter quelques décennies.
-
@Math Coss je connais aussi cette version... mais ça n'est pas le cas ici: le rectangle remplit EXACTEMENT le cadre au début ET à la fin. Il y a donc anguille sous roche... je vous laisse bien regarder la vidéo: le "truc" est dissimulé, mais on voit à un moment qu'il y a un détail qui ne va pas...

-
-
On voit assez bien l'espace manquant dans le rectangle final des cartes. Mais c'est très élégant !
-
N'est-ce pas Lewis Carroll qui a trouvé ce concept avec son fameux https://www.apmep.fr/IMG/pdf/Puzzle_Carroll_.pdf ?
Auquel cas, cela fait encore plus de décennies ! -
@Philippe Malot non je ne parlais pas de celle-ci. C'est un autre numéro consacré exclusivement au puzzle de Sherlock Holmes (et il introduisait également la pipe de Sherlock Holmes, qui ne servait à rien pour le tour mais qui était très sympa pour la présentation). Mais je n'avais pas vu le tour que vous avez partagé! C'est effectivement un puzzle très ressemblant, mais qui repose sur l'espace manquant entre les cartes.Dans le tour que j'ai partagé, le truc est différent: j'insiste sur le fait que l'aire du puzzle est exactement la même au début et à la fin (même pas un $\varepsilon$ de différence). Si vous regardez attentivement la vidéo et que vous vérifiez tout ce qui se passe au niveau du puzzle, vous comprendrez pourquoi
 J'en profite pour poser une question sur le Rubik's cube. Considérons l'effet suivant: un spectateur mélange un cube, le magicien en mélange un autre. À la fin, le magicien et le spectateur comparent leurs cubes, et ils trouvent qu'après leurs mélanges, les cubes ont une face en commun... puis deux, puis trois... en fait, les six faces sont identiques dans les deux cubes. Dans le post où je parle des cubes (cf plus haut dans ce fil), j'évoque Gregory Wilson et Henry Harrius qui proposent de tels effets (pour ceux que ça intéressent). La question est: le fait que les sixièmes faces soient identiques dans les deux cubes est-il vraiment surprenant? Autrement dit: si cinq des six faces correspondent, la sixième face est-elle automatiquement la même dans les deux cubes?
J'en profite pour poser une question sur le Rubik's cube. Considérons l'effet suivant: un spectateur mélange un cube, le magicien en mélange un autre. À la fin, le magicien et le spectateur comparent leurs cubes, et ils trouvent qu'après leurs mélanges, les cubes ont une face en commun... puis deux, puis trois... en fait, les six faces sont identiques dans les deux cubes. Dans le post où je parle des cubes (cf plus haut dans ce fil), j'évoque Gregory Wilson et Henry Harrius qui proposent de tels effets (pour ceux que ça intéressent). La question est: le fait que les sixièmes faces soient identiques dans les deux cubes est-il vraiment surprenant? Autrement dit: si cinq des six faces correspondent, la sixième face est-elle automatiquement la même dans les deux cubes?
-
@adrien2019 : Merci pour ce fil, j’ai pu trouver une variante du « three card monte » qui est maintenant un de mes tours préférés !
Pour ta question sur les cubes, la réponse est non : partons d’un cube résolu. Il est possible d’inverser l’orientation de toutes les arêtes jaunes. Cette configuration est indiscernable de celle où on effectue en plus (par exemple) une double-transposition de ces arêtes, si on ne regarde que les cinq faces qui ne sont pas la jaune. Par contre, si deux configurations sont les mêmes sur cinq faces, alors les coins sont les mêmes (chaque coin est uniquement déterminé par l’ordre circulaire de deux de ses couleurs). Je pense que mon argument montre que pour toute configuration et toute face donnée, il existe exactement (ÉDIT : au moins…) onze autres configurations indiscernables de celle-là en regardant toutes les faces sauf celle donnée.
EDIT : Ah c’est bon j’ai compris le truc du puzzle, je confirme aux personnes qu’il y a quelque chose de plus que le truc mathématique connu de la tablette de chocolat ! Je crois que j’avais vu ce tour à la télé quand j’étais petit, je suis content de le revoir ! -
@Georges Abitbol pour le three card monte, le "stand up monte" de Garett Thomas est excellent si vous ne connaissez pas déjà.Pour le Rubik's Cube, j'aurais pensé le contraire. Je ne comprends pas comment on peut inverser les arrêtes jaunes sur un cube résolu (pour moi, cela va avoir un impact sur les couleurs des faces adjacentes). Pourriez-vous détailler votre raisonnement?Autre idée qui m'est revenue. Je crois qu'il existe une théorie mathématique des origamis. Voici un tour intéressant: une enveloppe astucieusement conçue pour permettre de révéler quatre possibilités différentes selon la situation:
 Il est assez explicite sur comment s'utilise l'enveloppe, mais je n'ai aucune idée de comment le pliage est réalisé (je crois que ça lui a pris plusieurs années à concevoir).
Il est assez explicite sur comment s'utilise l'enveloppe, mais je n'ai aucune idée de comment le pliage est réalisé (je crois que ça lui a pris plusieurs années à concevoir). -
Ok j’essaierai de faire des photos. Le stand-up Monte est monstrueux !
-
J'ai finalement acheté le Corinda (The Thirteen Steps to Mentalism), qui comme je l'avais dit plus haut, contient un chapitre consacré aux effets les plus "mathématiques". Je vous mets en photo la table des matières consacrée à ce chapitre, pour ceux que ça pourrait intéresser (je n'en suis pas encore arrivé à ce chapitre, donc je ne peux pas vous en dire plus pour le moment). À l'origine, les chapitres ont été publiés indépendamment (sous forme de mensuels il me semble). Je n'ai pas de référence, mais peut-être qu'on peut encore trouver les chapitres individuellement, si quelqu'un est intéressé uniquement par celui-là et voudrait éviter d'acheter tout le livre.@Georges Abitbol effectivement le stand-up Monte est formidable! Je suis intéressé par les photos pour le Rubik's cube si vous avez le temps (je ne suis toujours pas convaincu qu'avoir cinq faces sur six n'impose pas la sixième).

-
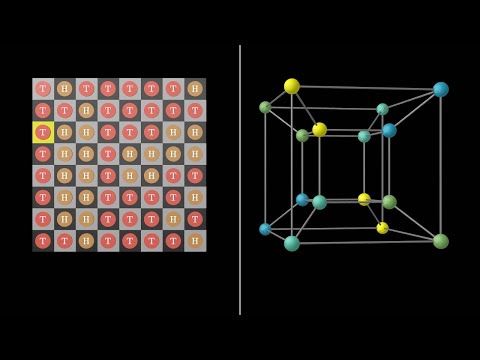
adrien2019 a dit :Je suis intéressé par les photos pour le Rubik's cube si vous avez le temps (je ne suis toujours pas convaincu qu'avoir cinq faces sur six n'impose pas la sixième).Si cinq faces sont faites, où peuvent aller les couleurs de la sixième ?Le seul cube pour lequel il peut y avoir un problème, c’est dans ce cas :
 Et encore : si cinq faces sont correctement orientées, la sixième aussi.Algebraic symbols are used when you do not know what you are talking about.
Et encore : si cinq faces sont correctement orientées, la sixième aussi.Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
J'avais commencé à prendre les photos, puis je m'étais dit que c'était plus pratique de chercher un site internet où il y aurait un applet java qui montrerait les cubes et les mouvements, puis j'ai écrit un début de réponse, et j'ai abandonné.En fait, avec un cube en mains et autour d'un sirop de pêche, ça prendrait cinq minutes à te montrer, mais à écrire c'est plus compliqué. Je vais tenter à nouveau, mais peux-tu juste me dire si tu connais des algorithmes de résolution du Rubik's Cube ? Si tu es familier avec les termes "arêtes", "coins", "centres", etc. ? Si tu sais qu'il y a des configurations qu'on peut obtenir en démontant le cube et en le remontant d'une certaine façon, mais qu'on ne peut pas obtenir sans tricher, i.e. en ne faisant que des mouvements autorisés, et comment les reconnaître ? Si tu réponds "oui" à tout ça, il me suffira de quelques lignes ; si c'est tout "non", il me faudra un peu plus de temps pour m'expliquer.
-
Oui à tout ça et je parlais de positions «légales ».
Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
N'ayant pas de smartphone, c'est un peu compliqué pour moi de faire des photos. Très rapidement, voici une méthode pour arriver à deux positions qui ont cinq faces en commun, mais pas six, à condition de parler le jargon Rubik's Cube.
Partir d'un cube résolu, face jaune en haut, et inverser l'orientation de toutes les arêtes de la face du haut. Pour inverser l'orientation de deux arêtes opposées de la face du haut, j'utilise MUMUMU2M'UM'UM'U2 (M pour tranche du milieu). C'est la position 1.
A partir de la position 1, faire une permutation des arêtes qui ne change pas l'orientation. Pour ça, je fais par exemple M2UMU2M'UM2. C'est la position 2.
Alors : la position 1 a la face blanche correcte, les faces orange, rouge, verte et bleue correctes sauf qu'elles ont une arête jaune, et la position 2 aussi. Par contre, si la position 1 et la position 2 ont les coins de la face jaune bien orientés, aucune arête n'est jaune et on peut obtenir n'importe quelle permutation paire des arêtes verte, bleue, rouge et orange qu'on y voit.PS : Correction de formule, merci @nicolas.patrois ! -
Le premier mouvement est MUMUMU2M'UM'UM'U2 (il manque un 2 à la fin).Je ne comprends pas : dans aucun des deux mouvements, cinq faces sont correctes et la sixième non.Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres