Exprimer en fonction de cos(x)

MathsU
MathsU
dans Analyse
sin(3x)/sin(x)

Réponses

  • ev
    ev
    Modifié (August 2022)
    Bonsoir.
    sin(3x) = sin(2x+x)
    Merci.
    Personne n'a raison contre un enfant qui pleure.


  • troisqua
    troisqua
    $4\cos^{2}\left(x\right)-1$

  • NicoLeProf
    NicoLeProf
    Modifié (August 2022)
    Bonjour,
    tu peux écrire $\sin(3x)=\sin(2x+x)$ puis je te conseille d'utiliser les formules d'additions et de duplications de trigonométrie : $\sin(a+b) = ...$ ?
    Tu as aussi : $\sin(2x)= ... $? et $\cos(2x)= ... $? 
    Enfin, je t'invite à préciser pour quels $x$ ton calcul est valable.
    En espérant avoir aidé ! ;)
  • MathsU
    MathsU
    Sin(3x)/sinx=sin2xCosx+SinxCos2x/sin
    2SinxCosxCosx/Sinx+SinxCos2x/Sinx
    2Cos^2x+Cos2x
    A ce niveau je ne parviens pas à exprimer en fonction de cos(x) 
  • MathsU
    MathsU
    Modifié (August 2022)
    troisqua a dit : $4\cos^{2}\left(x\right)-1$
    Il faut l'exprimer en fonction de cos x.
  • troisqua
    troisqua
    Ça tombe bien vu que c'est 4 fois le carré du cosinus de $x$ le tout ôté de 1 :)
  • MathsU
    MathsU
    Modifié (August 2022)
    NicoLeProf a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2375215/#Comment_2375215
    [Inutile de recopier un message présent sur le forum. Un lien suffit. AD]
    J'ai utilisé cette méthode sin(2x+x)=sin2xcosx+cos2xsinx
    En divisant par sinx
    J'obtiens 2(cosx)^2+cos2x
  • NicoLeProf
    NicoLeProf
    Modifié (August 2022)
    MathsU a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2375216/#Comment_2375216
    [Inutile de recopier un message présent sur le forum. Un lien suffit. AD]
    Tu connais une relation reliant $\cos(2x)$ et $\cos^2(x)$ je pense au vu de ce que tu as fait, qui est très bien.
    Concernant ta dernière remarque, en fonction de $\cos x$ signifie (je le comprends comme cela en tout cas) : comme une fonction de $\cos x$.
    Donc la réponse $4 \cos^2(x)-1$ est bonne dans la mesure où c'est bien l'expression algébrique d'une fonction de $\cos x$ (l'expression de la fonction $f : t \mapsto 4t^2-1$ en prenant $t=\cos x$.
  • troisqua
    troisqua
    Encore un effort et tu vas trouver ce que je t'ai donné ! Bonne recherche.
  • etanche
    etanche
    Modifié (August 2022)
    Trouver tous les $a,b$ entiers tels que $\dfrac{\sin(ax)}{\sin(bx)}$ s’exprime seulement avec du cosinus 
  • Thierry Poma
    Thierry Poma
    MathsU : bonsoir. Lorsque l'on vient sur ce forum, la moindre des choses et de dire "bonjour", d'écrire une phrase a minima expliquant ton problème, phrase agrémentée de symboles mathématiques et de conclure par un "merci". Je te remercie pour ta compréhension.
    Le chat ouvrit les yeux, le soleil y entra. Le chat ferma les yeux, le soleil y resta. Voilà pourquoi le soir, quand le chat se réveille, j'aperçois dans le noir deux morceaux de soleil. (Maurice Carême).
  • MathsU
    MathsU
    Bonsoir Thierry 
    Merci de m'avoir donné une leçon de morale. 
    Je ne manquerai pas de prendre votre conseil. 
    Cordialement.
  • JLapin
    JLapin
    Ca n'a rien avoir avec une leçon de morale en fait...
  • stfj
    stfj
    Modifié (August 2022)
    bonjour. Vu que tout est ramené à $\cos(a+b)=...$ et à $\sin(a+b)=...$, peut-être rappeler la relation fondamentale qui permet de retrouver ces résultats pénibles à mémoriser : $$\begin{bmatrix} \cos a & -\sin a \\ \sin a & \cos a \end{bmatrix}.\begin{bmatrix} \cos b & -\sin b \\ \sin b & \cos b \end{bmatrix}=...$$
    Sinon, pourquoi ne pas se l'intégrer entre deux valeurs sympathiques que quelqu'un proposerait ?
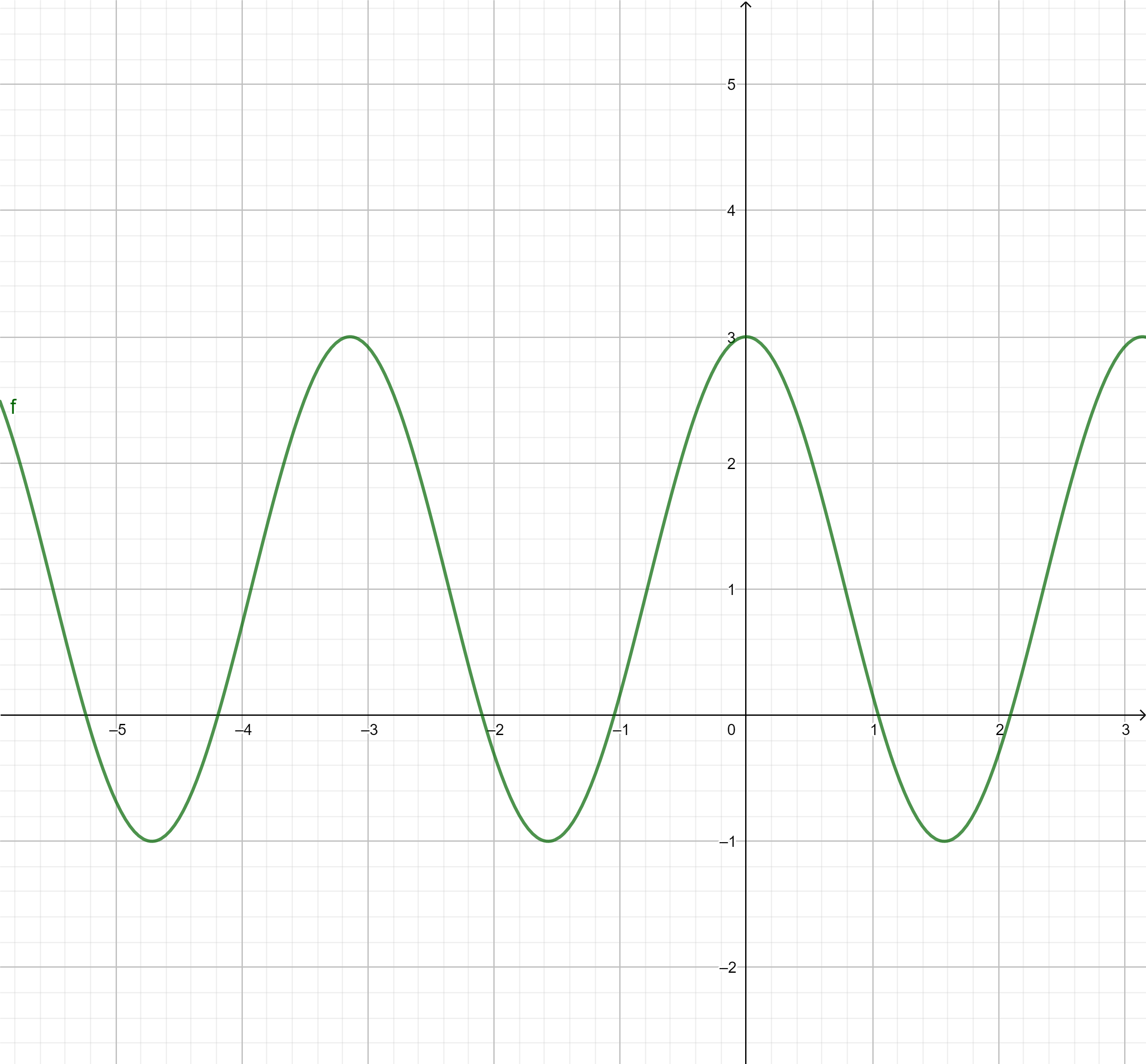    (Au fait, comment fait-on pour réduire la taille des images que l'on publie ?)
    [On clique sur l'image, apparaissent des manettes (handles) aux quatre coins. Sélectionner l'un et le tirer. :)AD]
  • troisqua
    troisqua
    Politesse sur un forum ? Mais pourquoi faire ? Ce ne sont pas des humains qui répondent sur un forum, ce sont des automates dévoués au questionneur et qui vivent dans un monde parallèle.  Et lui, ce qu'il veut, c'est juste $\frac{\sin(3x)}{\sin(x)}$ en fonction de $\cos(x)$ (et ne se rend d'ailleurs pas compte de ce que veut dire ce "en fonction de" ni probablement ne connaît pas la notation $\cos^2x$). Bref, ça y est, ça me redonne envie de poster ce sketch (en québécois c'est tellement plus savoureux):


  • stfj
    stfj
    @troisqua : à mourir de rire, ponctué par "Ta g..., j'vas t'tuer.". Par ailleurs, quid de l'intérêt de ma remarque ? :) Un petit $\arccos(\frac12)$ pour calmer les nerfs ? Bienvenue dans un monde paisible, où tout s'écoule fluidement, @MathsU :)
  • Math Coss
    Math Coss
    @srfj : je ne trouve pas le moyen mnémotechnique très efficace parce que 1) les matrices ne viennent pas dans les programmes assez tôt ; se rappeler les matrices de rotation est au moins aussi délicat que la formule d'addition ; 3) le calcul matriciel est une gageure.
    Mieux vaut se rappeler que $\exp(\mathrm i(a+b))=\cdots$
  • NicoLeProf
    NicoLeProf
    Tout à fait d'accord avec Math Coss pour le coup ! Il vaut mieux passer par les complexes qui seront sans doute plus familiers aux étudiants entrant en prépa ou à l'université ! :)
  • stfj
    stfj
    Modifié (August 2022)
    @Math Coss, @NicoLeProf, bonjour à tous-deux. Je ne partage pas entièrement votre avis à propos du conseil qui serait fait à des élèves de Terminale ou même à des élèves commençant leur propédeutique, conseil d'utiliser la fonction exponentielle complexe. Pour les meilleures d'entre eux, ne serait-ce pas gâcher quelques plaisirs à venir ? Mais je chipotte, évidemment :). Difficile parfois quand on enseigne d'éviter soi-même les paralogismes qu'on voudrait le plus possible épargner à nos élèves, n'est-ce pas ? Par contre, je crois -je n'en suis pas sûr- que les matrices et les bases du calcul matriciel sont devenus maintenant courants dans les classes terminales des lycées français. Et difficile d'imaginer qu'un élève ne connaisse pas alors les matrices de rotations dans le plan, n'est-ce pas ? Si c'était le cas, s'il ne les connaissait pas, plutôt que de lui enseigner que $\cos (a+b)=\cos a\cos b-\sin a \sin b$, il faudrait de toute urgence lui enseigner que la matrice d' "angle" le nombre réel $a$ est $$\begin{bmatrix} \cos a & -\sin a \\ \sin a & \cos a \end{bmatrix},$$ formule bien plus fondamentale pour le physicien, la chimiste, l'ingénieure, la géologue, la mathématicienne même. N'est-il pas ?
  • Riemann_lapins_cretins
    Riemann_lapins_cretins
    Pour le moyen mnémotechnique sur les formules d'addition et de soustraction : 

    "Les cosinus sont méchants, il reste entre eux et repoussent les sinus.
    Les sinus sont gentils, ils se mélangent avec les cosinus"
  • NicoLeProf
    NicoLeProf
    Modifié (August 2022)
    Bonjour,
    je viens de consulter les programmes de lycée et les matrices sont uniquement au programme de l'option "maths expertes" (enseignement facultatif) de Terminale comme les nombres complexes.
    Mais malheureusement, pas de lien à faire avec les matrices de rotations (on peut toujours en parler cela dit en effet surtout si on a un groupe d'élèves qui percutent bien en face de nous)...
    En terminale, une matrice est vue seulement comme un tableau et non comme la représentation d'une application linéaire dans une base. On fait seulement des liens avec les graphes et les suites.
    Alors que la théorie sur les nombres complexes est davantage étudiée (notamment le lien avec la géométrie et la trigonométrie).
    D'ailleurs la démonstration d'une des formules d'addition avec la forme exponentielle des nombres complexes est un attendu du programme de maths expertes en terminale. 
    Pour toutes ces raisons, je pense que le passage par l'exponentielle complexe est préférable (si on s'adresse à des élèves de terminale bien sûr).
Connectez-vous ou Inscrivez-vous pour répondre.

Bonjour!

Pour participer au forum, cliquer sur l'un des boutons :

Connexion S'inscrire

Catégories

In this Discussion

Qui est en ligne 7

AmadouMilas +5 Invités