Courbe paramétrée et tangente
Bonsoir
Je ne comprends pas d'où sort l'intervalle $[-1,1] \setminus \{0 \}$.
J'ai un peu honte, mais je ne comprends pas mon erreur dans ce qui suit...
On a $x'(t) \geq 0 \Leftrightarrow 1- \dfrac{1}{t^3} \geq 0 \Leftrightarrow 1 \geq \dfrac{1}{t^3} \Leftrightarrow t^3 \geq 1 \Leftrightarrow x \geq 1$
Pour $y'(t)$ pas de problème, il suffit d'écrire $y'(t)=\dfrac{t^2-1}{t^3}$.
Avec une deuxième méthode je trouve le bon résultat $x'(t)=\dfrac{ (t-1)(t^2+t+1)}{t^3}$.
Or, $\forall t \in [-1,1], \ t-1 \leq 0$ et $t^2+t+1 \geq 0$ donc si $t \in [-1,0]$ comme $t^3 \leq 0 $ alors $x'(t) \geq 0$ et si $t \in [0,1]$ comme $t^3 \geq 0$ alors $x'(t) \leq 0$.


Je ne comprends pas d'où sort l'intervalle $[-1,1] \setminus \{0 \}$.
J'ai un peu honte, mais je ne comprends pas mon erreur dans ce qui suit...
On a $x'(t) \geq 0 \Leftrightarrow 1- \dfrac{1}{t^3} \geq 0 \Leftrightarrow 1 \geq \dfrac{1}{t^3} \Leftrightarrow t^3 \geq 1 \Leftrightarrow x \geq 1$
Pour $y'(t)$ pas de problème, il suffit d'écrire $y'(t)=\dfrac{t^2-1}{t^3}$.
Avec une deuxième méthode je trouve le bon résultat $x'(t)=\dfrac{ (t-1)(t^2+t+1)}{t^3}$.
Or, $\forall t \in [-1,1], \ t-1 \leq 0$ et $t^2+t+1 \geq 0$ donc si $t \in [-1,0]$ comme $t^3 \leq 0 $ alors $x'(t) \geq 0$ et si $t \in [0,1]$ comme $t^3 \geq 0$ alors $x'(t) \leq 0$.


Réponses
-
C'est normal, puisque tu ne vois rien.
-
Et la limite j'ai aussi un problème.
$y(t) - y(1)=t^2 /2 + 1/t -3/2 $ et $x(t)-x(1)=t +1/2t^2 -1$.
Or, $\lim_1 y(t)-y(1)=0$ et $\lim_1 x(t)-x(1)=0$ on a une forme indéterminée $0/0$
-
Bonjour,Heureusement que tu es certifié, obtenu dans une pochette surprise cependant, car sinon je me demanderais quel niveau tu as obtenu en maths, car je pense que ceci se traite en L1 pour lever une pauvre forme indéterminée. Ceci doit même toujours se faire au lycée car tes numérateur et dénominateur ne sont quand même que des vulgaires polynômes, moyennant une petite transformation bien entendu.Et encore une fois, arrête de nous mettre tes corrigés à la noix.
-
Bonjour,
Ça me rappelle mes exos faciles de début de sup.
Cordialement,
Rescassol
-
Je n'arrive pas à lever la forme indéterminée je suis plus habitué à manipuler les limites en plus l'infini et moins l'infini avec les équivalents.
Comment on passe de la symétrie d'axe y=x à l'intervalle $[-1,1]$? Je ne vois pas d'où il sort...
-
Bonsoir,
A quoi sert d'habitude la découverte d'une symétrie dans l'étude d'une courbe ?
Tu ne connais pas les équivalents ailleurs qu'en l'infini ?
Cordialement,
Rescassol
-
À réduire le domaine mais je ne comprends la réduction que pour les fonctions périodiques.
Je ne comprends pas comment réduire le domaine pour une symétrie par rapport à la première bissectrice.
Je connais les équivalents au voisinage de 0 aussi. -
Bonsoir,
Soit $s: t \mapsto \dfrac{1}{t}$. Tu ne peux pas trouver un ensemble $E$ tel que $E\cup s(E)=\mathbb{R}$ et $E\cap s(E)=\emptyset$ à peu de chose près ?
> Je connais les équivalents au voisinage de 0 aussi.
T'as qu'à faire un changement de variable (même si ce qu'a dit JavierT plus haut est plus simple).
Cordialement,
Rescassol
-
D'accord merci j'ai compris pour l'axe de symétrie.
Si $E= [-1,1] \setminus \{0 \}$ alors $s(E)= \{ 1/t \ | \ t \in [-1,1] \} =\overline{E}$ on le voit graphiquement.
J'ai essayé d'utiliser les polynômes mais ça ne donne rien. Notons $\Delta=\dfrac{ y(t)-y(1)}{ x(t)-x(1)}$.
On a $\Delta=\dfrac{t^2/2 +1/t -3/2}{ t+ 1/2t^2 -3/2}=\dfrac{t^4+2t-3t^2}{2t^3 +1 -3 t^2}$ et on a encore une forme indéterminée...
En fait les équivalents sont utilisés pour des fonctions du genre $\sin x$ , $\tan x$ etc ... Ici je ne comprends pas comment les utiliser ni leur intérêt.
-
@OShine
ça devrait être interdit de poster un corrigé et de dire "je ne comprends pas le corrigé". Tu nous demandes de t'aider à comprendre une solution déjà imprimée, c'est quand même un comble.
Fais un effort, @OShine, ne poste plus jamais les corrigés des exos sur lesquels tu sèches.
On en arrive à une récursion assez vertigineuse, au fait que tu ne comprends pas ton corrigé, ni les indications qu'on te donne pour le comprendre, ni les explications sur ces indications. -
Ok mais là je ne parle plus du corrigé je parle de la limite en $1$ que je n'arrive pas à calculer.
Et aussi du raisonnement suivant que j'ai fait moi-même dont je ne comprends pas l'erreur :
$x'(t) \geq 0 \Leftrightarrow 1- \dfrac{1}{t^3} \geq 0 \Leftrightarrow 1 \geq \dfrac{1}{t^3} \Leftrightarrow t^3 \geq 1 \Leftrightarrow x \geq 1$.
-
Bonsoir,
Tu n'as jamais entendu parler de racine évidente d'un polynôme ?
Ça remonte à la 1ère.
Cordialement,
Rescassol
-
Bonsoir,petit tour ici avant de rejoindre mon lit... rien de très nouveau. "Quand le sage montre la lune, l'imbécile regarde le doigt"...Quand à la racine évidente, ce n'est pas la lune... elle est là où on la cherche!Bien le bonsoir...
-
Merci @Rescassol
Si on a : $\Delta=\dfrac{t^2/2 +1/t -3/2}{ t+ 1/2t^2 -3/2}=\dfrac{t^4+2t-3t^2}{2t^3 +1 -3 t^2}$
$1$ est racine évidente et même racine double de $P(t)=t^4+2t-3t^2 =(t-1)^2 t (t+2)$ et $Q(t)=2t^3 +1 -3 t^2 =(t-1)^2 (2t+1)$
Donc $\Delta= \dfrac{t (t+2)}{2t+1} \longrightarrow \dfrac{3}{3}=1$
Par contre mon erreur avec le $x'(t) \geq 0$ je ne la trouve pas.
-
erreur niveau collège, sans rire...$ 1 \geq \dfrac{1}{t^3} \Leftrightarrow t^3 \geq 1$tu es convaincu de ça ? Rien qui te gêne?EDIT: j'ose croire que tu cesseras définitivement de venir déverser tes viles remarques sur le niveau des candidats à l'agreg interne... les arcs paramétrés s'étudient au lycée et tu ne prends même pas la peine d'ouvrir un manuel !
-
Je ne trouve pas l'erreur depuis cet après-midi et ça m'énerve. Le passage à l'inverse renverse l'ordre des inégalités j'ai juste utilisé cette propriété.
Les arcs paramétrés au lycée ? J'ai étudié le cours sur les arcs paramétrés de MP... Il n'y a plus grand chose au programme, ça fait 5 pages de cours.
-
Tiens on va essayer : $1\geqslant \dfrac{1}{(-1)^3}$ donc $(-1)^3\geqslant 1$... cherche l'erreur.
-
"Le passage à l'inverse renverse l'ordre des inégalités"...
Essaie ton équivalence $\Bigl(1 \geq \dfrac{1}{t^3} \Leftrightarrow t^3 \geq 1\Bigr)$ avec $t<0$. -
Pardon mais c’est vraiment choquant…
-
Je sais que c'est faux mais je ne trouve pas vraiment l'erreur où elle se trouve. Pourquoi on a pas le droit de passer à l'inverse et de renverser l'inégalité ?
-
Ca t'énerve de ne pas réussir cette question, de ne pas voir ton erreur ?
Moi, pareil, j'ai eu le même sentiment à une époque de ma vie.
Pendant quelques années semaines, ça m'a énervé parce que j'étais incapable de trouver les bons coup au jeu de go. Je cherchais, et je ne trouvais pas. Aucune intuition, rien. Alors que d'autres trouvaient.
Et j'en ai tiré les conclusions, j'ai compris que j'étais nul pour cette activité là, et je me suis intéressé à d'autres activités, où je réussissais mieux.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
En fin d'année, quand tu prépareras tes cours pour tes élèves, tu retrouveras les éléments pour répondre à cette question ; Pourquoi on n'a pas le droit de passer à l'inverse et de renverser l'inégalité ?
En tout cas, il faudra que tu leur expliques, donc espérons que d'ici là, tu auras la réponse à cette question.
Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
@OShine tiens un petit cours rapide sur les inéquations http://villemin.gerard.free.fr/aMaths/ARITALGE/Inequat.htm
Regarde surtout le passage où il parle de l'effet miroir lorsqu'on multiplie par un nombre négatif. Là je me tâte sur quelle emote ajouter... celle-ci 🤣 ou bien celle-ci 😭 ? -
Assez dingue ce qui se passe sur ce fil. On dirait qu'OShine régresse à force de faire des exercices.
Je pense que même lui, normalement, n'aurait pas fait une faute pareille. C'est peut-être signe qu'il est temps de faire une pause avec les exercices et de se reposer un peu.
Après, à titre personnel je continue de trouver tous ces fils particulièrement gênants. On se demande même dans quel but OShine poursuit sa course effrénée vers les exercices de concours. Il a avoué lui-même ne pas vouloir faire l'agreg et, de plus, il ne semble ni prendre du plaisir ni s'améliorer. C'est vraiment une forme de masochisme malsain.
-
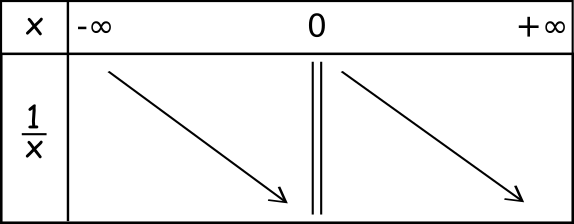
Fonction de référence.
 Karl Tremblay 1976-2023, je t'appréciais tellement.
Karl Tremblay 1976-2023, je t'appréciais tellement. -
Va te promener, profite de ce beau Week-End ensoleillé.
Il n'y a aucune urgence à écrire des bêtises, il sera toujours temps la semaine prochaine. Ou l'année prochaine.
Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
OShine le nombre 1 n'est pas négatif.
 Karl Tremblay 1976-2023, je t'appréciais tellement.
Karl Tremblay 1976-2023, je t'appréciais tellement. -
Pourquoi as-tu effacé ce que tu avais écrit il y a 1 heure environ ?
A titre pédagogique, pour montrer à des collégiens les erreurs les plus courantes, c'était un bon support.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Question $2$ :
On a $\gamma'(t)=(x'(t),y'(t)) =(1- \dfrac{1}{t^3},t-\dfrac{1}{t^2})=(1- \dfrac{1}{t^3}) (1,t)$. Posons $\vec{u}=(1,t)$ c'est un vecteur directeur de $\gamma'(t)$.
Pour trouver une équation de la tangente, prenons $M(x,y)$ on a alors $\det( M - \gamma(t) ,\vec{u}) =0$
Après calculs, on trouve $\boxed{t^3 -2t^2 x+2ty-1=0}$
Soient $(t_1,t_2)$ deux réels tels que $\gamma(t_1)$ et $\gamma(t_2)$ appartiennent à la tangente. On veut aussi que $\gamma(t_1)$ soit orthogonal à $\gamma(t_2)$, ce qui fournit $(\gamma(t_1) , \gamma(t_2))=0$ soit $1+t_1 t_2 =.$ et finalement $\boxed{t_1 t_2 =-1}$
On cherche donc les points tels que $t_1$ et $t_2$ soient racines du polynôme $P(X)=X^3-2x X^2+2y X-1$ et tels que $t_1 t_2 =-1$.
D'après les relations coefficients racines, $P(X)=1 \times (X^3 -\sigma_1 X^2+\sigma_2 X - \sigma_3= (X-t_1)(X-t_2)(X-t_3)$ avec $\sigma_1=t_1+t_2+t_3=2x$, $\sigma_2=t_1 t_2+ t_1 t_3 + t_2 t_3=2y$ et $\sigma_3 =t_1 t_2 t_3=1$.
Après calculs, on trouve la condition nécessaire $\boxed{y+x=-1}$.
Réciproquement , si $y+x=-1$ alors $P(X)=X^3-2xX^2 + 2(-1-x) X-1$
On remarque que $P(-1)=-1-2x+2(1+x)-1=0$ donc $1$ est racine de $P$. Ainsi, $\boxed{P(X)=(X+1)(X^2 + (2y+1) X-1)}$
Posons $Q(X)=X^2 + (2y+1) X-1$ son discriminant vaut $\Delta=(2y+1)^2+4 >0$ donc $Q$ possède deux racines réelles et $Q(X)=(X-t_1)(X-t_2)=X^2-\sigma_1 X+ \sigma_2$.
Par les relations coefficients-racines, on a $\sigma_1=t_1+t_2=-(2y+1)$ et $\sigma_2=t_1 t_2=-1$.
Une condition nécessaire est suffisante est donc que $t_1$ et $t_2$ sont racines de $P(X)=X^3-2x X^2+2y X-1$ avec $t_1 t_2 =-1$.
-
Manipuler les opérations élémentaires sur des inégalités niveau lycée ?... Donc, par récurrence, l'étude des fonctions polynomiales et de leurs pôles niveau L1, et quoi encore ? Voilà pourquoi tu te penses niveau agreg docteur !!!!
-
Je ne me pense rien du tout je trouve les exercices agreg docteur intéressants.
-
Il n'y a pas des lois contre l'acharnement thérapeutique ?
-
Les exos d'agrégation docteur sont plus faciles que les exos d'agrégation externe et interne.
-
Aucune importance, puisque dans tous les cas, tu ne sais pas faire !!La seule différence avec les imprudents qui veulent aller au sommet du Mont Blanc en tongs c'est qu'il n'y a pas besoin d'hélicoptère pour secourir O.S.
-
Tu as effacé ton message de 9h55. Ce n'est pas conforme à la charte. J'espère que les administrateurs vont remettre le message original.
Sinon, pour chaque question que tu poses, tu vas effacer tous tes messages quand tu croiras avoir compris ?Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
C'est humain de supprimer un message compromettant, quand on a dit une bêtise.
-
BonjourEn ce qui concerne le fait que la première bissectrice est axe de symétrie, @OShine ;
Soit $f(t)=(x(t),y(t))$ et notons $C:=Imf$ et $s:\R^2 \to \R^2, (x,y) \to (y,x)$. [$s$ est la symétrie par rapport à la première bissectrice (ce n'est pas difficile à démontrer).]
Les égalité ($x(1/t)=y(t)$ et $y(1/t)=x(t)$ pour $t$ différent de $0$) se réécrivent $f(1/t)=s(f(t))$, autrement écrit "le point de la courbe $C$ de paramètre $1/t$ est le symétrique du point de paramètre $t$. (Prenez des exemples de valeurs de $t$ si vous n'êtes pas convaincu : ce ne serait pas du temps perdu puisqu'ensuite toutes les études de courbes paramétrées, dans toute leur variété, se réduisent à ces pratiques qu'on acquiert petit à petit à force de pratique.)
Considérons enfin $t \to 1/t$. L'image de $[-1,1]-\{0\}$ est $R\]-1,1[$.
Voilà de nombreux sous-entendus du début du corrigé rapide proposé.remarque : cela amène une autre critique (de l'énoncé cette fois) où l'on fait l'abus de langage consistant à confondre l'arc $f$ et $C:=Imf$. Or, on sait l'importance en analyse complexe de la distinction qu'il ne faudrait donc jamais se lasser de faire pour des apprenants du moins, n'est-ce pas ?Cordialement, -
Je n'utilise jamais de règle d'inversion dans une inéquation. Je multiplie simplement l'inéquation $1 \geqslant \dfrac{1}{t^3}$ par $t^3$ et je pense au signe de $t^3$. Je fais ça depuis que je manipule des inéquations et des nombres négatifs. Collège, lycée ? Je ne sais plus. Mais je sais qu'après le lycée, j'ai fait 5 ans d'études avant d'avoir eu le droit de passer le, et avoir été admis au, CAPES. Personnellement face à des erreurs comme ça, je t'aurais foutu dehors au milieu même de ton oral. Tu te rends compte que chaque erreur que tu fais, chaque lacune que tu as, si tu ne t'en rends pas compte, tu risques et vas finir par les transmettre à tes élèves, et l'année d'après quand ils auront un prof compétent, ils seront largués de partout et vont tous décrocher des maths à cause de toi ? Ton incompétence a de vraies conséquences, tu peux toujours faire l'égoïste "m'en fous, on m'a donné ce poste, c'est pas moi le responsable" ou bien tu pourrais te comporter avec empathie pour tes élèves et, avant de penser à l'agreg interne pour ton petit confort personnel, essayer de garantir à ces enfants dont tu as la responsabilité au niveau des mathématiques un cours qui leur permettra de développer des connaissances sûres. Tu n'as vraiment aucune empathie pour ces enfants, peu importe ce que tu penses, tes actions montrent la vérité.
-
C'est vrai que là, on tombe sur des connaissances qu'il doit enseigner, c'est honteux. On pourrait penser, que sans être immensément brillant en maths, OShine fasse correctement son taf en collège. Mais là, on peut sérieusement en douter s'il ne pense pas à vérifier le signe d'un nombre quand il multiplie une inégalité membre à membre. Je suis à peu près certain qu'il a déjà fait cette erreur par le passé donc pas étonné qu'il récidive.
Et c'est là que pour moi, l'Education Nationale est en tort. Bien content de ne plus faire parti de ce navire quand on voit qu'elle n'assure ni le bien-être de ses enseignants, ni une reconnaissance salariale un peu digne d'un BAC+5 concours ni une qualité minimale de recrutement de ses agents pour qu'il soit apte à enseigner au moins au collège. -
[*** Modéré pour grossièreté. AD]Je vais peut-être vous faire peur, mais Oshine est loin d'être le pire qui a eu le CAPES. J'ai des eu des étudiants qui sont devenus certifiés qui étaient (et doivent encore être) à des années-lumière de Oshine.Il y a la rubrique maths et sociétés pour savoir comment on est arrivé à de tels recrutements. Mais maintenant que c'est fait, arrêtez de pourrir OSHINE sur ses fils mathématiques.
-
Tu parles sans savoir, Jaoapa, tu ne sais pas comment était OS quand il était étudiant. Et effectivement, la plupart des certifiés sont à des années lumières, heureusement. Quant à OS, il provoque les réactions par son refus de chercher seul tout en ayant des prétentions, et d'apprendre les maths du secondaire. Qui sème le vent récolte la tempête.
-
Bonjour,Même si on peut être d'accord sur le fond, le message de Joaopa, en particulier sa première phrase, est inadmissible sur un forum qui sait en général éviter les grossièretés.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.8K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 771 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres








