Subdivision centrale 2015
J'aimerais savoir comment on fait pour trouver l'idée pour commencer la question $2$ qui me semble extrêmement difficile.
J'ai le corrigé mais je ne comprends pas comment ils pensent à faire tout ça.
Dans la question $1$, on trouve $\forall i \in [|0,n|] \ a_i = F^{-1} \left( \dfrac{i}{n} \displaystyle\int_{a}^b f(t) dt \right)$ où $F(x)=\displaystyle\int_{a}^x f(t) dt$

Réponses
-
Les hypothèses sur $f$, qu'impliquent-elles sur $F:x\in[a,b]\mapsto \displaystyle\int_a^x\!\! f(t)\text{d}t$ ?
La question 1, comment se réécrit-elle en utilisant $F$? Que vaut $a_0$?
-
$F$ est strictement croissante car $F'$ s'annule qu'un nombre fini de fois et $F'=f$ avec $f$ positive.
Et $a_0=a$ et $a_n=b$ c'est le principe d'une subdivision.
Elle s'écrit $\boxed{F(a_{i+1})-F(a_i)=\dfrac{1}{n} F(b)}$
-
La limite doit être $ \dfrac{1}{\int_a^b f(t) dt} \times \int_a^b f(y) g(y) dy.$Encore une fois rien de difficile ici. C'est gros comme une maison que la somme est une somme de Riemann. De plus tu as le corrigé, cela doit être expliqué.
-
Comment tu fais pour deviner la limite ?
Le corrigé fait plein de calculs mais n'explique pas l'idée qui permet de deviner la limite. -
Il y a du $i/n$ donc ça fait penser aux sommes de Riemann.
-
Le corrigé n'utilise pas de sommes de Riemann...
Je ne vois pas trop où est la somme de RIemann.
Je comprends les lignes du corrigé et les calculs mais je ne comprends pas l'idée de la preuve qui nous mène à faire ces calculs et ces majorations.

-
A priori, tu ne sais pas jouer aux échecs. C'est certain.
Aux échecs, il y a un type de jeu, en parties très rapides (le Blitz). Imaginons une partie, avec une position un peu compliqué. Le bon joueur va parfois trouver à un moment un coup très efficace, et surtout totalement inattendu. Sans réellement réfléchir, le rythme de jeu ne permet pas de réfléchir plus de 4 ou 5 secondes à chaque coup.
Comment il devine ce bon coup, ça ne s'explique pas. Il pourra l'expliquer pendant des heures à un joueur débutant, le débutant ne saura pas le reproduire s'il a la même situation dans une partie.
Et le joueur doué (mais pas forcément brillant), il n'a pas besoin qu'on lui explique. Il n'aurait pas trouvé de lui même ce bon coup, mais après avoir vu un champion le faire, il est maintenant capable de le reproduire, de l'adapter à des situations similaires. Sans avoir besoin qu'on lui explique quoi que ce soit.
Comment les bons élèves trouvent les idées pour faire les exercices difficiles. Ben, parce qu'ils sont bons, tout simplement. Ils ont le petit don que tout le monde n'a pas. Si tout le monde avait les mêmes capacités en maths, ça se saurait !
En tant que prof, tu l'as déjà dit toi-même, tu avais l'année dernière des élèves que tu trouvais très doués, et d'autres beaucoup moins doués.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
La seule façon de s'en sortir c'est de ne pas regarder le corrigé et de faire l'exercice soi-même. Le mieux est de justifier son propre travail que celui des autres.
-
@lourrran c'est un livre pour étudiant donc s'il se veut pédagogique il doit expliquer le chemin du raisonnement.
La question $2$ est trop abrupte pour moi, détaillée en questions intermédiaires, j'arriverais sûrement à trouver des idées, mais là je suis incapable d'écrire une ligne de raisonnement sur une telle question.
On dirait une question d'écrit d'ENS ULM. -
N'importe quoi. !
Comme d'habLa seule idée à avoir c'est de voir qu'on a une somme de Riemann.
C'est vrai que tu aurais voulu qu'onexplique le corrigé et ensuite tu aurais eu des idées.
Le prochain exercice tu auras l'idée de regarder le corrigé, de dire que le corrigé n'explique pas bien et on aura la copie du corrigé dont on a rien à faire. -
Le lien entre Q1 et Q2 n'est déjà pas évident, car dans Q2 $g$ est à valeurs dans un espace vectoriel normé quelconque. On ne sait même pas qui est $g$.
Tu parles de somme de Riemann, mais je n'ai jamais vu de somme de Riemann dans un espace vectoriel différent de $\R$.
Je ne vois pas de somme de la forme $\dfrac{b-a}{n} \displaystyle\sum_{k=0}^{n-1} f(a+ k \dfrac{b-a}{n})$ pourtant je suis à l'aise avec les somme de Riemann en temps normal.
-
Faire l'exercice avec R est suffisant. Et comme tu es à l'aise avec les sommes de Riemann c'est bon, tu n'as pas besoin d'aide. Tu es tellement à l'aise que tu ne vois même pas qu'il y a une somme de Riemann.Edit le temps normal n'existe pas pour toi.
-
Tu parles de somme de Riemann mais le corrigé n'utilise pas cette méthode donc elle n'est peut être pas si évidente.
Où est la somme de Riemann ? Tu utilises l'uniforme continuité comme le corrigé ?
Dans le corrigé ils partent de $\dfrac{F(b)}{n} g(a_i)= \displaystyle\int_{a_i}^{a_{i+1}} f(t) g(a_i) dt$ ce qui est logique vu la question $1$.
Mais comment ils devinent qu'on doit montrer : $\dfrac{F(b)}{n} \displaystyle\sum_{i=0}^{n-1} g(a_i) \longrightarrow \displaystyle\int_{a}^{b} f(t) g(t) dt$ ?
-
On te l'a dit : on reconnait évidemment une somme de Riemann.Si les contraintes du programme ne permettent pas d'étendre un résultat connu pour les fonctions à valeurs réelles, rien n'empêche de traiter d'abord un cas particulier puis d'adapter la preuve du théorème dans le cas particulier pour traiter le cas général sans le théorème hors-programme. Ca fait partie de ce qui est demandé aux candidats au concours : connaitre ses démos des résultats du cours et, pour les meilleurs, les adapter à d'autres situations. C'est sans doute pour ça que l'énoncé n'est pas plus détaillé.Tu devrais lire l'entretien de feu Claude Deschamps et ses conseils aux élèves vers la fin. C'est beaucoup plus intéressant pour comprendre comment trouver une dynamique de travail en maths que le rapport du concours Bidule sur la question 3c réussie par moins de 15% des candidats.
-
Je ne vois pas la somme de Riemann dans cet exercice, je ne vois pas qui sont $a,b,k$.
J'ai relu le cours de MP et les sommes de Riemann sont bien au programme de MP, pour des fonctions vectorielles à valeurs dans un espace vectoriel normé de dimension finie. J'ai parlé trop vite.
D'ailleurs, on adapte la preuve de MPSI en raisonnant sur les composantes de $f$ dans une base de $E$.
-
On peut ne pas se contenter de subdivisions équiréparties.
-
La somme des $g(a_i)$ n'est pas une somme de Riemann.
On a pas de $g(a + i(b-a) /n) $ -
Il y a une somme de Riemann avec une subdivision équi répartie. Mais si tu prétends qu'il n'y a pas de somme de Riemann, pas de problème passe à la suite.Nous ne sommes pas là pour expliquer le corrigé à chaque fois . Si tu ne comprends pas l'idée comme toujours c'est parce que tu ne fais jamais rien par toi même.Donc tu peux passer à l'exercice suivant, ceci sans suivre nos conseils répétés milles fois. Donc tu nous copieras le corrigé et tu demanderas des explications du corrigé qu'on ne lira pas.
-
Donne la somme de Riemann alors le corrigé n'en parle pas.
Il utilise une autre méthode avec la continuité uniforme. -
Je n'ai pas envie de lire le corrigé mais je suis presque certain qu'il utilise qu'on a une somme de Riemann et redémontre la convergence vers l'intégrale correspondante.Comme tu es à l'aise avec les sommes de Riemann tu aurais pu faire l'exercice tout seul.
-
Vous êtes en train de lui dire : cherche par toi-même, sans lire le corrigé.
Mais vous savez très bien qu'en cherchant par lui-même, il ne trouvera jamais rien.
Quand il cherche des exercices de lycée compliqués (concours général), il ne trouve rien. Même avec le corrigé, il ne comprend pas.
Comme dit Deschamps, il faut des bases solides pour attaquer les classes prépas. Et les bases solides ne sont pas là. Point final.
Donc le bouquin d'exercice de M', qu'il l'offre à un étudiant concerné, c'est ce qu'il peut faire de mieux.
Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
@Louran, si @Os suivait nos conseils, c'est-à-dire ne pas regarder le corrigé, on aurait pu lui donner progressivement 1 puis 2 ou 3 indications qui donnent rapidement le résultat. On a une somme de Riemann, avec une subdivision régulière de l'intervalle [0,1],... et peut être il aurait fait un morceau de l'exercice. On utilise le théorème de convergence qu'il a cité. L'exercice est alors plié en 2 lignes. En annexe on peut redémontrer ce théorème, ce que le bouquin fait je pense (peut être parce que les sommes de Riemann ne sont pas ua programme ?) . Mais une chose à la fois et on n'est pas obligé de faire comme le livre car la démonstration du livre parait plus compliquée alors qu'il est plus simple de le faire sur un intervalle de référence tout de même.Là il y aurait un certain travail de sa part et une progression serait possible.Depuis toujours il ne cherche qu'à comprendre les corrigés et souhaite qu'on l'aide à comprendre. D'abord ce n'est pas une bonne méthode et cela demande pour nous un travail très long sur un forum. C'est-à-dire qu'on se fatigue 10 fois plus que lui avec des résultats négligeables puisqu'il n'aura pas cherché.
-
Je ne trouve pas la somme de Riemann dans cet exercice pourtant c'est dans mon livre le théorème et sa démonstration même pour des fonctions vectorielles.
Généralement je trouve les exercices sur les sommes de Riemann faciles. -
Ton livre est tout pourri !
-
Voici un exercice dans le même style, avec des sommes de Riemann basées sur des subdivisions non régulières. Je mets mon corrigé directement après, c'est juste pour l'information d' @OShine.
Soit $f:[0,a]\rightarrow[0,b]$, continue strictement croissante, surjective. Soit $g=f^{-1}$.
1) Montrer l'égalité : $ab=\displaystyle\int_0^a f(x)\,\text{d}x+\displaystyle\int_0^bg(x)\,\text{d}x$
2) Montrer que, pour $u\in[0,a]$ et $v\in[0,b]$ : $uv\le\displaystyle\int_{0}^{u}f(x)\,\text{d}x+\displaystyle\int_{0}^{v}g(x)\,\text{d}x$
3) Interprétations graphiques?
==========================
1) Posons $x_k=\dfrac{ka}{n},\;y_k=f(x_k)$, pour $0\le k\le n$.
Les $x_k$ forment une subdivision régulière $\sigma$ de $[0,a]$.
La fonction $f$ étant croissante, les $y_k$ forment une subdivision (quelconque) de $[0,b]$.
On considère les sommes de Riemann : $S_n=\dfrac an \displaystyle\sum_{k=1}^n f(x_k),\ S'_n= \displaystyle\sum_{k=0}^{n-1}(y_{k+1}-y_{k})g(y_k)$
Lorsque $n\rightarrow+\infty$, $S_n$ tend vers $\displaystyle\int_ 0^{a}f(x)\,\text{d}x$.
La fonction $f$ est continue sur le segment $[0,1]$. Elle y est donc uniformément continue (Théorème de Heine).
Le "pas" de la subdivision $\sigma'$ tend donc vers $0$ lorsque $n\rightarrow+\infty$.
Ainsi $S'_n\to\displaystyle\int_{0}^{b}g(x)\,\text{d}x$ quand $n\rightarrow+\infty$.
D'autre part : $$\begin{array}{l}S_n+S'_n=\dfrac an \displaystyle\sum_{k=1}^n y_k+ \displaystyle\sum_{k=0}^{n-1}(y_{k+1}-y_{k})x_k\\\quad=\dfrac an \displaystyle\sum_{k=1}^n y_k+ \displaystyle\sum_{k=0}^{n-1}x_ky_{k+1}- \displaystyle\sum_{k=0}^{n-1}x_ky_k\\\quad=\dfrac an \displaystyle\sum_{k=1}^n y_k+ \displaystyle\sum_{k=1}^nx_{k-1}y_k- \displaystyle\sum_{k=0}^{n-1}x_ky_k\\\quad= \displaystyle\sum_{k=1}^{n-1}\Bigl(\underbrace{\dfrac an-x_k+x_{k-1}}_{=0}\Bigr)y_k+\Bigl(\dfrac an+x_{n-1}\Bigr)b\\\quad=ab\end{array}$$Quand $n\rightarrow\infty$, l'égalité $S_n+S'_n=ab$ donne : $\displaystyle\int_{0}^a f(x)\,\text{d}x+\displaystyle\int_{0}^b g(x)\,\text{d}x=ab$
2) On se donne $u\in[0,a]$ et $v\in[0,b]$.
D'après ce qui précède, on a : $\displaystyle\int_{0}^{u} f(x)\,\text{d}x+\displaystyle\int_{0}^{f(u)}g(x)\,\text{d}x=uf(u)$. Ainsi : $$\begin{array}{l}\displaystyle\int_{0}^{u} f(x)\,\text{d}x+\displaystyle\int_{0}^{v} g(x)\,\text{d}x-uv\\\quad=\displaystyle\int_{0}^{u} f(x)\,\text{d}x+\displaystyle\int_{0}^{f(u)}g(x)\,\text{d}x\\\qquad+\displaystyle\int_{f(u)}^{v}g(x)\,\text{d}x-uv\\\quad=u(f(u)-v)+\displaystyle\int_{f(u)}^{v}g(x)\,\text{d}x\\\quad=\displaystyle\int_{f(u)}^{v}\bigl(g(x)-u\bigr)\,\text{d}x\end{array}$$Rappelons que $g$, tout comme $f$, est croissante :
Si $f(u)\le v$, $u\le g(x)\le g(v)$ sur $[f(u),v]$. Si $v\le f(u)$, $g(v)\le g(x)\le u$ sur $[v,f(u)]$.
Dans tous les cas: $\displaystyle\int_{f(u)}^v\bigl(g(x)-u\bigr)\,\text{d}x\ge 0$.
Compte tenu du calcul précédent, on en déduit : $\displaystyle\int_{0}^u f(x)\,\text{d}x+\displaystyle\int_{0}^v g(x)\,\text{d}x\ge uv$
3) Le schéma ci-dessous illustre l'idée de la démonstration de la première question.
On y voit la subdivision $(x_k)$ de $[0,a]$, et la subdivision $(y_k)$ de $[0,b]$.
La somme de Riemann $S_6$ de $f$ est représenté par des hachures obliques.
La somme de Riemann $S'_6$ de $g$ est représentée par un nuage de points.
On voit bien comment $S_6$ et $S'_6$ s'emboîtent de sorte que $S_6+S'_6=ab$.
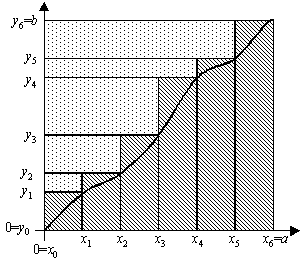
Quand $n\rightarrow\infty$ on devine que $S_n$ et $S'_n$ tendent respectivement vers l'intégrale de $f$ sur $[0,a]$ (aire du domaine situé sous la courbe $y=f(x)$ et dans le rectangle $[0,a]\times[0,b]$) et vers l'intégrale de $g=f^{-1}$ sur $[0,b]$ (aire du domaine situé au-dessus de la courbe $y=f(x)$ et dans le rectangle $[0,a]\times[0,b]$). Le fait que la somme des deux aires soit égale à $ab$ est aussi particulièrement évident sur ce graphique.
Le dessin ci-dessous illustre la question 2. On s'est placé ici dans le cas $v\ge f(u)$.
L'intégrale de $f$ sur $[0,v]$ est hachurée horizontalement, et celle de $g$ sur $[0,v]$ est hachurée verticalement.
On voit que la somme de ces deux aires dépasse $uv$ (le rectangle grisé) :
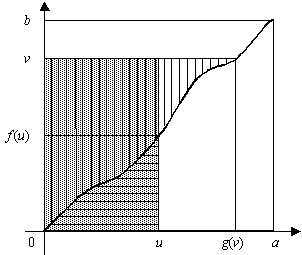
-
@gairequin "ton livre est tout pourri " oui (mais un peu exagéré tout de même) l'auteur a fait un choix mais rien n'interdit de faire plus simple.Puisque @Os insiste: On remarque que $\sum_{i=0}^{n-1} g(a_i)=\sum_{i=0}^{n-1} h(i/n) $ où l'on a posé $h(x)= g(F^{-1} (x \int_a^b f(t) dt )).$ C'est bien une somme de Riemann avec subdivision régulière.Il reste à vérifier les hypothèses et on en déduit que la limite est $\int_0^1 h(x) dx$ + un petit travail pour exprimer cette dernière intégrale en fonction de $f$ et $g$. Si on veut justifier la limite il est préférable de travailler sur cette subdivision régulière.Edit: en plus de l'exercice de @Jmf je te propose ce petit exo sur les sommes de Riemann.Déterminer la limite de $u_n=n \ln(2)-\sum\limits_{i=0}^n \dfrac{1}{1+\frac{i}{n}}$.
-
Bd2017 la limite vaut moins l'infini.
-
Je ne pense pas et pourquoi?Remarque: c'est un exercice classique sur les sommes de Rieamann
-
Donc $-\infty=-\dfrac{3}{4}$.
-
@jmf ton exercice est encore plus difficile que celui d'origine

@bd2017
Soit $n \geq 1$.
$\dfrac{ u_n}{n} = \ln(2) - \dfrac{1}{n} - \dfrac{1}{n} \displaystyle\sum_{i=1}^n f( i /n)$ où $f(x)=\dfrac{1}{1+x}$
Donc $\dfrac{ u_n}{n} \longrightarrow \ln(2) -\displaystyle\int_{0}^1 \ln (1+x )dx =0$
Je ne vois pas comment obtenir la limite de $u$.
Pour mon exercice en cours je vais chercher comment faire maintenant que je vois la somme de Riemann. Dans le cours, il n'est pas dit que les subdivisions doivent être régulières. -
@OShine
On écrit $u_n=n\ln 2 - \displaystyle\sum_{k=0}^{n}\dfrac{1}{1+k/n}=n(\ln 2-v_n)$ avec $v_n=\dfrac{1}{n}\displaystyle\sum_{k=0}^{n}\dfrac{1}{1+k/n}$
Or $v_n$ est une somme de Riemann de $f:x\mapsto\dfrac{1}{1+x}$ sur $[0,1]$, donc $\displaystyle\lim_{n\to+\infty}v_n=\displaystyle\int_0^1f(t)\text{d}t=\ln2$.
Ainsi $\displaystyle\lim_{n\to+\infty}u_n=n\Bigl(\ln2-\displaystyle\lim_{n\to+\infty}v_n\Bigr)=n(\ln2-\ln2)=n\times 0=0$ 😉 -
C'est inutile de sommer de $1$ à $n$ pour se retrouver avec le terme $1/n$ en plus. Pour la somme de Riemann tu peux sommer de $0$ à $ n-1.$Effectivement on a$$\int_0^1 f(x) dx =1/n \sum_{i=0}^{n-1} f(i/n) + o(1)\qquad (1)$$C'est une autre façon de dire ce que tu as rappelé.Si on multiplie le tout par $n$, le $o(1)$ n'est pas assez précis pour obtenir le résultat.C'est-à-dire qu'on doit pousser plus loin le développement de $\int_0^1 f(x) dx.$Comment faire ? D'abord remarquer que $f$ est $\C^{infty}$ pour être tranquille par la suite.Il faut donc reprendre la démonstration du (1) c'est du cours et aller un peu plus loin que la démonstration.J'en ai assez dit pour faire le travail...Reprendre la démonstration du théorème du cours (comme quoi les démonstration de cours sont utiles..)Edit. Je n'ai pas vu le message de @Jmf !!! Si les vents sont contraires au sens de la marche on est mal barré.

-
@jmf il y a un problème dans ta démo, une somme de Riemann va de $0$ à $n-1$ ou de $1$ à $n$.
Je reviens à l'exercice de départ. On a $\dfrac{1}{n} \displaystyle\sum_{i=0}^{n-1} g(a_i)= \dfrac{1}{n} \displaystyle\sum_{i=0}^{n-1} g( F^{-1} \left( \dfrac{i}{n} \displaystyle\int_{a}^b f(t) dt \right) )$
Posons $h(\dfrac{i}{n})=g( F^{-1} \left( \dfrac{i}{n} \displaystyle\int_{a}^b f(t) dt \right)$
Ainsi, $\boxed{\dfrac{1}{n} \displaystyle\sum_{i=0}^{n-1} g(a_i)=\dfrac{1}{n} \displaystyle\sum_{i=0}^{n-1} h(\dfrac{i}{n})}$
On reconnaît une somme de Riemann.
Montrons que $h$ est continue par morceaux sur $[0,F(b)]$. $h : [0,F(b)] \longrightarrow E$.
$F$ est continue sur $[a,b]$ et établit une bijection de $[a,b]$ sur $[0,F(b)]$ donc $F^{-1}$ est de continue sur $[0,F(b)]$ et par suite $h$ est continue sur $[0,F(b)]$.
Je bloque ici, la fonction $h$ est trop compliquée, je ne vois pas comment obtenir le résultat et en plus les bornes correspondent pas à $[0,1]$.
Peut-être que le corrigé a eu raison d'utiliser l'autre méthode, il me semble que les sommes de Riemann sont ici beaucoup trop compliquées.
-
J'avais défini la fonction $h$. Il serait bien d'en tenir compte. De plus le domaine de définition de $h$ n'est pas correct.Je ne comprends pourquoi tu déformes les définitions qu'on te donnent. Il n'y a rien de compliqué dans la définition de $h$ mais si tu écris n'importe quoi, ne soit pas étonné d'être bloqué.
Deux remarques qui sont encore du grand n'importe quoi ? C'est exaspérant.OShine a dit :@jmf il y a un problème dans ta démo, une somme de Riemann va de $0$ à $n-1$ ou de $1$ à $n$.
Peut-être que le corrigé a eu raison d'utiliser l'autre méthode, il me semble que les sommes de Riemann sont ici beaucoup trop compliquées.Après avoir dit que les sommes de Riemann ne sont pas un problème pour toi ! -
-
Je n'ai jamais vu de somme de Riemann aussi compliquées avec des fonctions composées et des réciproques. Dans les exos de MPSI c'était déterminer $\lim \displaystyle\sum_{k=0}^{n-1} \sin( k \pi /n)$ des trucs comme ça.
Je ne comprends pas pourquoi le domaine de définition de $h$ est faux. On a $F^{-1} : [0,F(b)] \longrightarrow [a,b]$ et $g : [a,b] \longrightarrow E$ donc $g \circ F^{-1} : [0,F(b)] \longrightarrow E$.
Je ne dis pas n'importe quoi sur les sommes de Riemann, dans le cours les sommes vont de $0$ à $n-1$ ou de $1$ à $n$. Il n'y a pas de somme de $0$ à $n$.
Théorème (MPSI) :
Si $f \in CM([a,b],\C)$ alors $\dfrac{b-a}{n} \displaystyle\sum_{k=0}^{n-1} f(a+ k \dfrac{b-a}{n}) \longrightarrow \displaystyle\int_{a}^b g(t) dt$
Coroallaire (MPSI) :
Si $f \in CM([a,b],\C)$ alors $\dfrac{b-a}{n} \displaystyle\sum_{k=1}^{n} f(a+ k \dfrac{b-a}{n}) \longrightarrow \displaystyle\int_{a}^b g(t) dt$
-
Oui j'ai lu un peu vite la remarque mais on est tellement habitué que cela devient un réflexe.J'ai donné l'expression de h(x) c'est dingue tout de même. Et ne pas pas voir que $h$ est définie sur [0,1] c'est un peu (beaucoup) dingue.Ensuite j'utilise le théorème sur les sommes de Riemann dans le cas le plus simple possible (a=0, b=1 et h continue) . Et tu trouves que c'est compliqué. Bravo.Et ajouter que les auteurs ont eu cette raison de proposer leur démonstration, on est bien dans le grand n'importe quoi.Edit laisse tomber l'autre exo, lui il est un peu plus difficile (mais sans plus) mais je ne suivrai pas tes élucubrations qu'on va retrouver à chaque ligne.
-
@jmf je ne sais pas, ce n'est pas la formule du cours. Et dans les exercices que j'ai traités c'était toujours de $0$ à $n-1$ ou de $1$ à $n$.
@bd2017 d'accord merci.
On a $\forall x \in [0,1] \ h(x)= u \circ v \circ w (x)$ avec :- $w(x)=x \displaystyle\int_{a}^b f(t) dt$. On a $\forall x \in [0,1] \ \ w(x) \in [0,F(b)]$ par croissance de $F$.
- $v(x)=F^{-1} (x)$. On a $\forall x \in [0,F(b)] \ \ w(x) \in [a,b]$.
- $u(x)=g(x)$. On a $\forall x \in [0,1] \ \ u(x) \in E$.
Ainsi $\boxed{\dfrac{1}{n} \displaystyle\sum_{i=0}^{n-1} g(a_i) \longrightarrow \displaystyle\int_{0}^1 h(x) dx}$
Or $\displaystyle\int_{0}^1 h(x) dx = \displaystyle\int_{0}^1 g \left( F^{-1} (x \displaystyle\int_{a}^b f(t) dt \right) dx$
Je bloque ici pour simplifier l'intégrale.
-
-
C'est bien ce que je craignais
-
Tiens Oshine sois honnête pour une fois. Est-ce que tu as appris des choses sur les 3 semaines que tu as passées sur l'exo 1 de l'agreg externe. Tu penses que tu as perdu du temps ou non? Qu'est-ce que tu as retenu?
Allez un peu d'honnêteté -
Noobey j'ai appris ce que sont les formes de Jordan. Pour la culture.
L'exercice n'est pas assez détaillé.
Je crois qu'en maths on perd souvent du temps à comprendre des exos qu'on ne saura pas refaire seul.
-
A mon avis l'exo de l'agreg externe est facile pour les gens qui ont déjà étudié un bouquin sur les formes de Jordan.
-
Malheureusement c'est ta manière de fonctionner ce que tu décris...OShine a dit :Je crois qu'en maths on perd souvent du temps à comprendre des exos qu'on ne saura pas refaire seul.
Il faut que tu en change ! En maths, il faut, au contraire, comprendre les exercices que l'on cherche, pour savoir les refaire seuls.
On t'a conseillé maintes et maintes fois de choisir des exercices de plus faible niveau, pour que tu apprennes à travailler, et que tu apprennes à te débrouiller seul.
Ta méthode actuelle ne fonctionne pas ! -
Citation : Je crois qu'en maths on perd souvent du temps à comprendre des exos qu'on ne saura pas refaire seul.
Ne généralise pas trop vite. Il y a une chose qui est évidente, c'est que tu perds ton temps à (essayer de) comprendre des exos que tu ne sauras pas refaire seul.
Si tu commences à t'en rendre compte, c'est déjà ça. Il y a plein de gens qui te le disent depuis des années, et tu commences à les croire.
Mais si on doit en tirer une règle générale, ce serait : En maths , quand on essaie de faire des exercices de niveau ENS alors qu'on a un niveau lycéen modeste, on perd du temps à comprendre des exos qu'on ne saura pas refaire seul.
Mais c'est une règle beaucoup plus générale : Pour devenir un musicien (ou un écrivain ou un sportif ou un matheux ou ... ) de tout premier plan, il faut du travail, mais il faut aussi de la méthode, et des qualités innées.
Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Tiens changeons d'exos: Montre que $A=\begin{pmatrix}-2&-3&-4\\-1&0&0\\2&2&3\end{pmatrix}$ et $B=\begin{pmatrix}-9&72&52\\1&-5&-4\\-3&20&15\end{pmatrix}$. Puis montre qu'une matrice est à valeurs propres de partie réelle strictement négatives si et seulement si $\exp(tA)\underset{t\rightarrow+\infty}{\longrightarrow}0.$
-
Je ne sais pas vraiment combien vaut K.
Amédé j'aimerais j'aimerais bien que Bd2017 m'explique comment simplifier l'intégrale compliquée de l'exercice original.
Je chercherai ton exo sur un autre fil.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.8K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 771 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres







