Axiomatisation de R
Voici un extrait d'un livre sur l'axiomatisation de $\mathbb R$.

Ensuite, l'auteur donne des théorèmes justifiables donc par cette axiomatisation.
Ce que je ne comprends pas, c'est qu'il donne ce théorème :
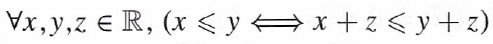
N'est-ce pas un axiome ? Que cela soit le sens direct ou réciproque, c'est bien l'axiome 3) qui est appliqué.

Ensuite, l'auteur donne des théorèmes justifiables donc par cette axiomatisation.
Ce que je ne comprends pas, c'est qu'il donne ce théorème :
N'est-ce pas un axiome ? Que cela soit le sens direct ou réciproque, c'est bien l'axiome 3) qui est appliqué.
Réponses
-
Le sens direct (gauche vers droite), c’est exactement l’axiome 3, sans aucun travail (un changement de lettres dans ce cas n’est pas un travail).Le sens réciproque, c’est une application de l’axiome 3 avec un tout léger travail : choisir d’utiliser l’axiome 3 en particularisant « $c=-z$ ». J’ose dire que ce n’est pas immédiat.C’est dans ce sens que je comprends les choses.
-
Bonjour Dom,
Je me suis fait la même réflexion.
Mais en supposant que x + z <= y + z, les nombres x + z et y + z sont considérés comme des réels, on pourrait les noter respectivement X et Y.
Puis on ajoute -z pour chaque membre (qu'on pourrait noter Z), du coup cela revient au premier sens. -
Bonjour Endomorphisme.Une application facile d'un axiome n'est plus un axiome, mais un théorème. C'est tout.La notion de "théorème" n'est pas liée à la difficulté de la preuve, seulement au fait que ce n'est pas directement un axiome.Cordialement.
-
Quel est ce livre sur l'axiomatisation de $\mathbb R$ ?
-
Bonjour,
Il est important de comprendre qu'être axiome ou théorème ne sont pas des propriétés intrinsèques de propositions, d'ailleurs, si on prend comme définition de "théorème" que c'est une proposition conséquence des axiomes, alors les axiomes sont des théorèmes (puisque $a\Rightarrow a$).
On peut faire une analogie avec les éléments d'une base d'un ev, qui sont bien des vecteurs.Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
gerard0 : d'accord !
Chaurien : ce n'est pas un livre dédié spécifiquement à l'axiomatisation de R, c'est le premier cours d'analyse MPSI de Jean-Marie Monier (5e édition).
Médiat_Suprème : pas trop compris mais convaincu par la réponse de gerard0.
mais convaincu par la réponse de gerard0. -
Désolé de ne pas avoir été clair, une autre façon de le dire : axiomes et théorèmes sont des objets de même nature (ce sont des propositions), on fait jouer un rôle particulier à certaines de ces propositions (les axiomes) comme on fait jouer un rôle particulier aux éléments d'une base (ou même plus précisément d'une famille génératrice).Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
En fait, la réponse de Médiat me fait réfléchir. Pourquoi ne pas appeler axiome tout ce qui ne se démontre pas lors à un "instant donné" ?
Par exemple, on démontre en général le théorème de Heine (version L1) avec le théorème de Bolzano-Weierstrass. Dans la démo, ce dernier est un axiome, puisqu'on ne le démontre pas. On utilise d'ailleurs tout un tas d'axiomes qu'on ne justifie pas dans la démonstration. -
Parce que ce n'est pas du tout une pratique courante.Endomorphisme a dit :En fait, la réponse de Médiat me fait réfléchir. Pourquoi ne pas appeler axiome tout ce qui ne se démontre pas lors à un "instant donné" ?
-
Endomorphisme, votre question montre que vous avez compris le fond de la question, néanmoins JLapin a raison, ce n'est pas l'usage.
Pour mener à bien une démonstration, on part de certaines propositions et on applique les règles de déduction pour obtenir des théorèmes. Il reste à savoir ce que sont les "certaines propositions", ce sont soit des axiomes, soit des théorèmes déjà démontrés, qu'il n'y a aucune raison de re-baptiser.Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
Merci Médiat !
-
Cependant, un intervenant régulier du forum de géométrie parlait très souvent d'axiome de Pythagore; pour dénoncer la faiblesse de la formation en géométrie actuelle.
-
Soit $(E,\multimap)$ un ensemble muni d'une loi de composition interne. Soit $H$ une partie de $E$. On note $T(H)$ l'intersection de toutes les parties $F$ de $E$ contenant $H$ et telles que pour tous $x,y\in E$, si $x\multimap y \in F$ et si $x\in F$ alors $y\in F$. Alors $T(H)$ est alors exactement l'ensemble des éléments $t$ de $E$ pour lesquels il existe un entier $n$ et un $n$-uplet $(x_1,\ldots,x_n)$ tels que $x_n=t$ et pour tous $i\leq n$, $x_i\in H$ ou bien il existe $j,k\in \{1,\ldots,i-1\}$ tels que $x_k \multimap x_i = x_j$.Un tel $n$-uplet s'appelle une "preuve de $t$ dans $H$" et les éléments de $T(H)$ s'appellent les "théorèmes de $H$".Maintenant, étant donné un entier $n$ et un $n$-uplet $u=(x_1,\ldots,x_n)$, peut-on construire une partie $Y$ "naturelle" de $E$ telle que $(x_1,\ldots,x_n)$ est une preuve de $x_n$ dans $Y$? La réponse est oui, en effet définissons par récurrence (sur $k\in \{1,\ldots,n\}$) un $n$-uplet $(H_k)_{1\leq k \leq n}$ de parties de $E$ en posant $H_1:=\{x_1\}$ et pour tout $k$ $H_{k+1}$ s'il existe un couple $(p,q)$ d'entiers tels que $1\leq p,q \leq k$ et $x_p = x_q \multimap x_k$ et $H_{k+1}=H_k$ dans le cas contraire.Alors $H_n$ est la plus petite partie $X$ de $E$ telle que $(x_1,\ldots,x_n)$ est une preuve de $x_n$ dans $X$.Le langage ensembliste n'est utilisé ci-dessus que pour la clarté de l'exposition et tout est algorithmique.On peut tout à fait appeler "axiomes de la preuve $(x_1,\ldots,x_n)$" les éléments de $H_n$ ci-dessus. C'est ce que Christophe C veut dire quand parfois il affirme que "tout texte est une preuve". Cependant l'usage courant désigne par "axiome" les éléments d'un ensemble $A$ désigné explicitement à l'avance et dont on s'efforce pour déterminer pour des éléments particuliers de $E$, s'ils appartiennent à $T(A)$ ou non.Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$.
-
Il me semble que, si je m'en tiens à la théorie de la démonstration, la plus petite partie qui prouve $x_n$ est $\{x_n\}$. En fait, dans votre texte, il manque la définition de $X$.
Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
Médiat_SuprèmeC'est vrai cependant je parle de la plus petite partie telle que le $n-uplet$ $(x_1,\ldots,x_n)$ est une preuve de $x_n$ ce qui n'est pas exactement la même chose.Quant à $X$ cette lettre est liée dans ma phrase suivante (qu'on pourrait écrire si on insistait pour mettre des formules, sous la forme $H_n = \bigcap \{X \mid (x_1,\ldots,x_n) \text{ est une preuve de }x_n \text{ dans } X\}$).Certes le monde comprend les tournures de phrase comme $H_n$ est le plus petit objet tel que (...) $H_n$ (...) mais elle m'a toujours choqué (on pourrait considérer que c'est du pinaillage mais bon).Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$.
-
Pour que ma remarque soit plus claire, j'aurais mieux compris avec $(x_1, \ldots,x_n)$ est une preuve de $x_{n+1}$.Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
Peut-être que les notions sont plus faciles à implémenter en s'arrangeant pour que la conclusion ne fasse pas partie de la preuve dans la définition. Je n'ai pas vérifié.
Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
Je profite du sujet et du pseudo de l'auteur pour poser une grande question de ma vie : pourquoi utilise-t-on la terminologie "axiomes de la structure d'espace vectoriel" lorsqu'il s'agit de définir un espace vectoriel ?
-
On dit axiomes de la théorie des groupes, axiomes de la théorie des relations d'ordre, etc., et bien sûr à chaque fois il s'agit de définition (vocabulaire qui peut prendre des formes très différentes) mais le mot "axiome" impose une forme précise à cette définition.
On utilise plutôt le mot "définition" pour nommer une propriété (qui est souvent une proposition), donc qui peut être utilisée comme axiome pour une ou des théories.Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
La définition d'un espace vectoriel est une formule de la forme $P(E)$ qui dit "$E$ est une liste $(E_0,K_0,+,\times, ...)$ telle que (...)"Quand on parle "d'axiome(s) d'espace vectoriel" on veut juste dire qu'on ajoute $P(E)$ à la liste des hypothèses avec lesquelles on travaille.Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$.
-
De l'extérieur ça ressemble plus à une tradition qu'autre chose. Je ne vois pas bien la nuance.
-
Il n'y a aucun problème, sauf si on veut à tout prix avoir un seul sens pour chaque mot; ce qui n'est pas possible.
Quand on étudie une structure, elle a un certain nombre de propriétés de base, qui vont servir de point de départ, c'est normal de les appeler axiomes.
Cordialement. -
Un axiome n'est jamais rien d'autre qu'une phrase rajoutée à une liste (et ce de manière arbitraire); à partir de cette liste on peut produire des raisonnements.
Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
Arbitraire, pas vraiment, en tout cas pas au hasard, il y a toujours une raison au choix d'un axiome. et je ne comprends pas votre dernière expression "on peut produire des raisonnements.", les axiomes d'une théorie ne produisent pas de nouveaux raisonnements, mais de nouveaux théorèmes (à l'aide des raisonnements (règles d'inférence) valides pour la logique choisie (elle aussi).Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse -
Un texte : R.pdf (univ-rennes1.fr)
-
Dans ce fil : Trouver une suite de rationnels qui converge vers un réel quelconque — Les-mathematiques.net, j'ai publié un document avec 34 façons de définir $\mathbb R$ dont cette méthode qui trouve sa source chez Eudoxe de Cnide (il y a presque 3000 ans)Il ne faut pas respirer la compote, ça fait tousser.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres









