Moyenne essais statistiques
Bonsoir,
Si un évènement a une probabilité de succès de 1%, et qu'à chaque essai la probabilité augmente de 0.2%, comment puis-je calculer combien d'essais en moyenne faut-il pour que cet évènement se produise ?
J'ai fait un petit script python qui me retourne une moyenne de 24 essais environ, mais je ne sais pas comment trouver cette solution mathématiquement.
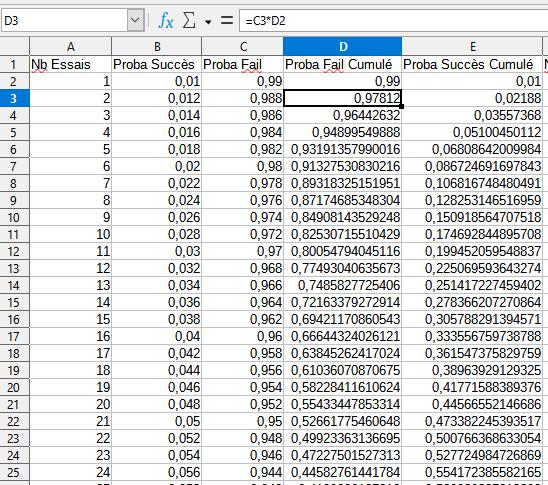
J'ai tenté de faire quelques calculs dans un tableau, si je comprends bien la médiane serait de 22 essais ? Car la probabilité cumulée est de 50%.
Merci d'avance pour votre aide.
Si un évènement a une probabilité de succès de 1%, et qu'à chaque essai la probabilité augmente de 0.2%, comment puis-je calculer combien d'essais en moyenne faut-il pour que cet évènement se produise ?
J'ai fait un petit script python qui me retourne une moyenne de 24 essais environ, mais je ne sais pas comment trouver cette solution mathématiquement.
J'ai tenté de faire quelques calculs dans un tableau, si je comprends bien la médiane serait de 22 essais ? Car la probabilité cumulée est de 50%.

Merci d'avance pour votre aide.
Réponses
-
Bonsoir.
On peut déjà fixer les idées en nommant un peu les variables. On considère une suite $(X_n)_{n\geq 1}$ de variables aléatoires indépendantes avec $X_k\sim \text{Ber}(0.01+0.002(k-1))$. On s'intéresse à la variable $Y=\inf \{k\geq 1\mid X_k=1\}$. On peut alors calculer (comme vous l'avez fait) la probabilité de l'événement $\{Y=n\}$ :
$$\mathbb P(Y=n)=\mathbb P\Big(\{X_n=1\}\cap\bigcap_{k=1}^{n-1}\{X_k=0\}\Big)=\big(0.01+0.002(n-1)\big)\prod_{k=1}^{n-1}\big(0.99-0.002(k-1)\big)
$$ L'espérance de $Y$ est alors donnée par
$$\mathbb E[Y]=\sum_{n\geq 1}n\mathbb P(Y=n).
$$ Je ne sais pas si on peut faire vraiment plus. WolframAlpha propose de l'écrire de manière plus condensée à l'aide des symboles de Pochhammer, mais je ne crois pas que ce soit judicieux.
Bon courage ! -
A l'aide du code suivant, je retrouve également une moyenne empirique proche de $24$ pour un $10000$-échantillon.
import random def experience(): k=1 while random.random()>0.01+0.002*(k-1): k+=1 return k n=100000 s=0 for i in range(0,n): s+=experience() print(s/n) [color=#FF0000]>> 24.11378[/color] -
D'après ton tableau, je pense que tu voulais dire : "la probabilité augmente de 0.002" plutôt que "la probabilité augmente de 0.2%" qui généralement signifie "la probabilité est multipliée par 1.02".
Si on note $T$ la variable aléatoire donnant l'instant du 1er succès, et $p_n$ la probabilité de succès à l'instant $n$ alors pour tout $n\in\{0,\dots,495\}$, $p_n=0.01+n\times 0.002=\frac{n+5}{500}$ et \[\mathbb{P}(T=n)=p_n\prod_{k=0}^{n-1}(1-p_k).
\] On peut en déduire l'espérance de $T$ :
\[\mathbb{E}(T)=\sum_{n=1}^{495}\mathbb{P}(T\geq n)=\sum_{n=1}^{495}\prod_{k=0}^{n-1}(1-p_k).
\] Une petite implémentation Python donne la valeur exacte sous forme de fraction... mais ce n'est guère mieux.Fraction(15737313105895866219254551340965147267404222786659393467681509663697452 43463975351837687017207765067138025075450562124427075461663464272645380772121174 36339731586951038897225407381783940203702997686590224459657117722619555869130977 09002792779644994166043472798841924102854133561352850022622082464732909966280079 69825831121787334805023603662463353126521788262571132132640130229112795838770836 18506437788880703846729883338111029704807473405528520491319439261901142156746567 23496629241626262108494455837392694598047134875545182520390122587958463368308575 90989483808374506553574291639767677411925066462530638257517561147468768935317342 95430395556409503391040956830973508104061542980386585058902060799814272368115838 70437469634268186089746308506110413233015992757144623115300504936198354533033164 35069411734527516797078777113418949072208004159501685587749335558985920698203914 90797685184732698988131628726735796838926812851256709950802383111057131340292505 90329764871100144547002684768921791939913939163436119689804902909383415736753532 9777439979044839287291928769689048405462124471206237718107298854935638322873, 65 03898174780929261347610186843748766600232098438213222754936333476963906311117258 55084043818310679982122611391892374412073402025719535200239021426299117984286683 48568069998353047847269798942917742156950880225507494013848410093526545487119359 71467005433280328384167367769621148776305791834478614961204393372810602478938019 59082325313004312036234383402057595168580035355914957359178271673689998697732872 56562116361335805783740890076471168269939786278993552631497381699053029042608446 02631077686390152821563899695984690552190153478431781059878120626881263387664578 59574821043224801542237401008605957031250000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000000000000000 000000000000000000000000000000000000000000000000000000000000000)
-
Merci pour vos réponses. Cependant je n'ai pas du tout le niveau requis pour comprendre vos formules, je m'attendais à ce que ce soit plus simple (ce n'est pas un travail scolaire, juste un problème qui me passait par la tête). :-D
Donc c'est compliqué de trouver un résultat mathématiquement, on doit faire une approximation par l'ordinateur ? -
Ce n'est pas du tout compliqué : on t'a tous les deux donné un résultat exact obtenu en quelques lignes.
Tout cela est abordable avec simplement les notions de proba vues au lycée.
Cependant, on ne peut pas donner une écriture simple de ce résultat parce qu'il n'en existe pas.
Je t'ai donné la valeur exacte sous forme de fraction irréductible... on n'a pas franchement envie de l'utiliser telle quelle ! -
Bonjour
Effectivement, comme le fait remarquer bisam, c'est assez élémentaire. Je vais peut-être donc préciser nos calculs pour qu'ils soient compréhensibles par quelqu'un qui ne fait pas trop de mathématiques.
La première étape était de fixer quelques notations :
On se donne une suite de variables aléatoires $(X_n)_n$ indépendantes, avec $X_k$ suivant la loi de Bernoulli de paramètre $p_k=\displaystyle\frac{n+5}{500}$ (pour $k\leq 495$, $1$ sinon). Cela signifie juste que $X_k$ vaut $1$ avec probabilité $p_k$ et $0$ sinon. Pour chaque réalisation de la suite de variables, on note $T$ le plus petit indice $k$ tel que $X_k=1$. On remarque que comme $p_{495}=1$, $T$ sera toujours inférieur à $495$.
La deuxième étape consistait à calculer la loi de $T$, autrement dit, la probabilité que $T$ vaille $n$, pour toutes les valeurs de $n$. Faisons le calcul pour les premiers indices. Pour que le $T$ vaille $0$, il faut que $X_0=1$ :
$$\mathbb{P}(T=0)=\mathbb{P}(X_0=1)=0,01$$
Pour que $T$ vaille $1$ il faut que $X_1$ vaille $1$, mais aussi que $X_0$ vaille $0$ (sans quoi on aurait $T=0$). Ainsi
$$\mathbb{P}(T=1)=\mathbb{P}(X_0=0\text{ et }X_1=1).
$$ On a supposé les $X_n$ indépendants. On peut donc écrire :
$$\mathbb{P}(T=1)=\mathbb{P}(X_0=0)\times \mathbb{P}(X_1=1)=(1-p_0)\times p_1.
$$ De manière générale, pour que $T=n$, il faut que $X_n=1$, et que pour tout $i<n$, $X_i=0$. Encore une fois grâce à l'hypothèse d'indépendance :
$$\mathbb{P}(T=n)=\mathbb{P}(X_0=0)\times \mathbb{P}(X_1=0)\times ...\times \mathbb{P}(X_{n-1}=0)\times \mathbb{P}(X_n=1)=(1-p_0)\times (1-p_1)\times ...\times (1-p_{n-1})\times p_n.
$$ Généralement, on écrit ce produit de manière concise
$$p_n\prod_{k=0}^{n-1}(1-p_k).
$$ La dernière étape consiste à calculer l'espérance. Comme pour une variable aléatoire qui prendrait un nombre fini de valeurs, on doit faire la somme des valeurs $n$ que peut prendre $T$, pondérées par la probabilité $\mathbb{P}(T=n)$ :
$$\mathbb{E}[T]=0\times \mathbb{P}(T=0)+1\times \mathbb{P}(T=1)+\ldots
$$ qu'on écrit à nouveau à l'aide d'un symbole
$$\mathbb{E}[T]=\sum_{n=0}^{+\infty}n\mathbb{P}(T=n).
$$ Comme $T$ ne peut pas valoir $496$, $497$,... (car $X_{495}=1$ avec probabilité $1$), cette somme est finie
$$\mathbb{E}[T]=\sum_{n=0}^{495}n\mathbb{P}(T=n).
$$ On obtient donc la formule annoncée
$$\mathbb{E}[T]=\sum_{n=0}^{495}np_n\prod_{k=0}^{n-1}(1-p_k).
$$ bisam proposait une alternative impliquant les probabilités que $T$ soit supérieur $n$ qui est peut-être plus naturelle avec ce genre de problème.
En espérant que nos formules paraissent moins compliquées comme ça.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres