Dynamique du solide
Bonjour,
Voici un problème que je croyais simple et sur lequel je bloque.
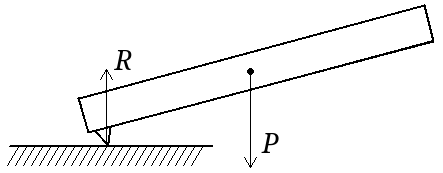
C'est un problème de dynamique du solide. Soit un solide $S$ ne ressentant que son poids $P$ et une force de réaction $R$ en un point donné. Le point de contact n'a pas de force de friction et peut librement glisser sur la partie fixe. En d'autres termes, les forces $R$ et $P$ sont pûrement verticales, et le point de contact se déplace.
Nous connaissons la masse $m$ et matrice d'inertie $I$ du solide.
Question : quelle est la valeur de la force de réaction ?
J'ai beau retourner le problème dans tous les sens, j'ai toujours plus d'inconnues que d'équations. Équations :
translation : $R + P = m \cdot a$
rotation : $R \cdot d = I_{yy} ( \dot \omega + \omega^2)$
(avec d la distance horizontale entre le contact et le CG)
Inconnues : $R$, $a$, $\dot \omega$
Quelle équation ajouter ?...
Voici un problème que je croyais simple et sur lequel je bloque.
C'est un problème de dynamique du solide. Soit un solide $S$ ne ressentant que son poids $P$ et une force de réaction $R$ en un point donné. Le point de contact n'a pas de force de friction et peut librement glisser sur la partie fixe. En d'autres termes, les forces $R$ et $P$ sont pûrement verticales, et le point de contact se déplace.
Nous connaissons la masse $m$ et matrice d'inertie $I$ du solide.
Question : quelle est la valeur de la force de réaction ?

J'ai beau retourner le problème dans tous les sens, j'ai toujours plus d'inconnues que d'équations. Équations :
translation : $R + P = m \cdot a$
rotation : $R \cdot d = I_{yy} ( \dot \omega + \omega^2)$
(avec d la distance horizontale entre le contact et le CG)
Inconnues : $R$, $a$, $\dot \omega$
Quelle équation ajouter ?...
Connectez-vous ou Inscrivez-vous pour répondre.

Réponses
Une relation entre $a$ et $\omega$ ?
Une idée : la force $\vec{R}$ ne travaille pas, donc la conservation de l'énergie mécanique donne une équation qui ne fait pas intervenir $R$, ce qui devrait permettre d'éliminer certaines inconnues. Je ne sais pas si ça marche.
Remarque, je nomme $x$ l'axe horizontal (orienté vers la droite), $z$ vertical vers haut, les angles sont orienté dans le sens direct en $(O,x,z)$ et j'ai pris $y$ orienté vers celui qui regarde l'image, ce met le bazar par rapport aux conventions habituelles.
Je nomme $G$ la position du point de gravité (c'est souvent une mauvaise convention, mais disons que ça passe ici), disons aussi que $\omega$ est l'angle de l'axe de la barre par rapport à l'horizontal ($\omega=k\pi$ quand elle est à plat). On a fait une projection sur un plan (de toute façon avec données du problème, la composante verticale de la vitesse du centre de masse ainsi que la vitesse de rotation dans le plan horizontale resteront constants sans que ça change quoi que ce soit à R).
Nommons $A$ le point de contact de la barre (le point de la barre, qui peut se déplacer avec elle). On a une contrainte, en nommant $z$ l'axe vertical, $\forall t: z_A(t)=0$, ce qui implique aussi par dérivation successive que la vitesse et l'accélération verticale de ce point est aussi nulle.
Donne l'équation cinétique qu'impose cette contrainte sur $z_A$ dans les variables qui t'arrangent (moi je conseille fortement $z_G$ la hauteur du centre de gravité, $\omega$ ainsi que leurs vitesses et accélérations tu vas voir pourquoi). Note: si on nomme $l$ la distance entre les projections de $G$ et $A$ sur l'axe horizontale quand la barre est horizontale et $h$ leur différence de hauteur dans la même condition, tu devrais avoir un truc du genre (ça dépend de tes conventions et puis il faut que je ne sois pas trop mauvais en géométrie aussi) $z_A=z_G - l'\text{cos}(\omega +\delta)$ avec $l'=\sqrt{l^2+h^2}$ et $\delta=\text{arctan}\left(\frac{h}{l}\right)$.
Maintenant la dynamique: Si tu cites les bons théorèmes (ici: centre de masse et d'autre part premier théorème de König, dans ce cadre, je ne suis pas certain de la pertinence des approches lagrangienne ou bilan énergétique) tu as:
1) $\frac{d^2 z_G}{d^2 t}= -g +\frac{R}{m}$ (ou $m$ est la masse totale de la barre. Edit: j'avais fait une erreur d'inattention, désolé si il y a eu un $m$ à la place du $g$ ).
2) Équation du moment angulaire propre (c'est à dire par rapport au centre de masse) : $ J_{yy} \frac{d^2 \omega}{d^2 t} = \left(\vec{GA} \wedge \vec{R} \right)\cdot \vec{e_y} $ (Si je ne me suis pas trop planté dans les conventions d'orientation) tu fais bien gaffe, parce que $\vec{GA}$ dépend vachement de $\omega$, ici tu devrais avoir un truc du genre $\vec{GA}\cdot \vec{e_x} = -l' \text{sin}(\omega +\delta)$ (attention, ça dépend encore de tes conventions géométriques)
Je te laisse recoller les morceaux, mais je crois que tu as assez d'information pour connaître la valeur de $R$ en fonction de deux variables pertinentes (au choix: $(\omega, \frac{d \omega }{dt} )$ ou $(z_G, \frac{d z_G}{dt})$ ).
En fait la réponse était très simple
En effet, on sait que l'accélération du point de contact est nulle normalement à la paroi. On a donc:
$a + d (\dot \omega + \omega^2) = 0$
Ce qui rajoute une équation sans ajouter d'inconnue.
La formule pour l'expression de l'accélération du point de contact peut se trouver ici : http://sii-tannarelli.com/contenus_opale/mouvement_solide_gen_auroraW/co/solide_champ_vecteurs_acceleration.html
https://physics.stackexchange.com/questions/102120/equation-of-motion-for-a-falling-rod-with-one-end-touching-a-frictionless-surfa