Les probas en 2023 en classe de troisième et la théorie naïve des ensembles
Bonjour,
Je suis professeur de collège et ai toujours été perplexe sur l'introduction il y a quelques années maintenant des probas en collège. Prétendre faire une introduction aux probabilités sans disposer d'aucun élément -presque - de théorie des ensembles naïve me paraît toujours une gageure.
Mon livre de référence sur le sujet est le belin 2008 dont le directeur d'ouvrage est Claude Deschamps.
Avec juste trois notations mathématiques: des lettres majuscules$( A, B, C, D, E, F, M)$ pour désigner des événements ; une notation ad hoc $(\overline{A}$ ou "non $A$") pour l'événement contraire; $p(A)$ pour la probabilité $p$ d'un événement $A$, le Belin (chapitre Statistiques et probabilités) réussit l'exploit de présenter un cours cohérent, accessible à des élèves ne disposant d'aucune connaissance de théorie naïve des ensembles, sur une notion pourtant basée depuis presque un siècle maintenant sur la théorie naïve des ensembles.
Pour se limiter évidemment aux probabilités sur un ensemble fini $U$ de cardinal Card$(U):=n$, une probabilité sur $U$ est une application de l'ensemble $\mathcal{P}(U)\to [0,1]$ telle que $pU=1$; pour $A=\{x_1,...,x_p\}\subset U, p(A):=\sum p(\{x_i\})\color{red}(*)$
Le Belin réussit l'exploit de (1) donner une définition statistique de la probabilité d'un événement élémentaire; (2) donner comme propriété : la probabilité d'un événement est égale à la somme des probabilités des éventualités qui le composent.
Comme quoi c'est faisable à condition pour un enseignant de continuer à croire qu'une majorité d'élèves apprend son cours, et surtout multiplie les exercices et les exemples. C'est sur ce dernier point que je voudrais partager : répartitions "filles-garçons" dans des collèges, dé à trois faces (Card $\mathcal{P}(U)=2^3=8)$, à quatre faces, à six faces, ... pièce de monnaie, jeu de carte, roue de loterie avec des fractions de la roue coloriées, urne avec des boules, roulette de casino, bataille navale ...
Je recherche des exemples de probabilité sur des ensembles finis permettant de pallier comme dans le Belin à l'absence de connaissances de théorie des ensembles naïve pour néanmoins arriver à armer mes élèves pour ce qui les attend au lycée. Par exemple, le dé à 3 faces, on l'aura compris, me permet d'explorer simplement avec mes élèves tous les événements de façon plus intéressante que le jeu de pile ou face ainsi que de décrire entièrement, de A à Z, la probabilité associée $\color{red}(*)$
Je suis professeur de collège et ai toujours été perplexe sur l'introduction il y a quelques années maintenant des probas en collège. Prétendre faire une introduction aux probabilités sans disposer d'aucun élément -presque - de théorie des ensembles naïve me paraît toujours une gageure.
Mon livre de référence sur le sujet est le belin 2008 dont le directeur d'ouvrage est Claude Deschamps.
Avec juste trois notations mathématiques: des lettres majuscules$( A, B, C, D, E, F, M)$ pour désigner des événements ; une notation ad hoc $(\overline{A}$ ou "non $A$") pour l'événement contraire; $p(A)$ pour la probabilité $p$ d'un événement $A$, le Belin (chapitre Statistiques et probabilités) réussit l'exploit de présenter un cours cohérent, accessible à des élèves ne disposant d'aucune connaissance de théorie naïve des ensembles, sur une notion pourtant basée depuis presque un siècle maintenant sur la théorie naïve des ensembles.
Pour se limiter évidemment aux probabilités sur un ensemble fini $U$ de cardinal Card$(U):=n$, une probabilité sur $U$ est une application de l'ensemble $\mathcal{P}(U)\to [0,1]$ telle que $pU=1$; pour $A=\{x_1,...,x_p\}\subset U, p(A):=\sum p(\{x_i\})\color{red}(*)$
Le Belin réussit l'exploit de (1) donner une définition statistique de la probabilité d'un événement élémentaire; (2) donner comme propriété : la probabilité d'un événement est égale à la somme des probabilités des éventualités qui le composent.
Comme quoi c'est faisable à condition pour un enseignant de continuer à croire qu'une majorité d'élèves apprend son cours, et surtout multiplie les exercices et les exemples. C'est sur ce dernier point que je voudrais partager : répartitions "filles-garçons" dans des collèges, dé à trois faces (Card $\mathcal{P}(U)=2^3=8)$, à quatre faces, à six faces, ... pièce de monnaie, jeu de carte, roue de loterie avec des fractions de la roue coloriées, urne avec des boules, roulette de casino, bataille navale ...
Je recherche des exemples de probabilité sur des ensembles finis permettant de pallier comme dans le Belin à l'absence de connaissances de théorie des ensembles naïve pour néanmoins arriver à armer mes élèves pour ce qui les attend au lycée. Par exemple, le dé à 3 faces, on l'aura compris, me permet d'explorer simplement avec mes élèves tous les événements de façon plus intéressante que le jeu de pile ou face ainsi que de décrire entièrement, de A à Z, la probabilité associée $\color{red}(*)$
Réponses
-
On peut même simplifier en gardant de la rigueur.Puisque l’univers est fini, on peut se passer du mot « application ». Il suffit de l’expliciter, par exemple dans un tableau (de valeurs).Aussi, on parle parfois de « loi de probabilité » à la place de « probabilité » mais ce n’est qu’une remarque.Dans les énoncés, faire vérifier qu’il s’agit bien d’une (loi de) probabilité me semble très pertinent (chaque probas est entre 0 et 1, la somme vaut 1).Enfin, je plussoie la notation entre accolades pour les événements.Suggestion : Appeler et noter $\Omega$ l’univers, n’est-ce pas « la classe » ?
-
Je pose une question sérieuse : il y a quoi de réellement intéressant et instructif à faire en probabilités au collège ?
-
C’est en effet une question sérieuse.Puis-je la poser pour Pythagore ou les fractions ?
Pour revenir à l’avocat du diable.
Le plus important est selon moi de distinguer « j’ai deux issues » de « j’ai une chance sur deux ».Je parle d’une portée sociétale (oui, oui, il m’arrive d’être optimiste…). -
@Dom : $U$ pour "Univers des possibles" me satisfait. Il y a une autre notation que j'aimerais populariser : dans un espace affine $(\mathcal{E},E,v)$, $v:\mathcal{E}\times \mathcal{E}\to E, (A,B)\mapsto v(A,B)$. C'est la classe quand tu n'as pas la flèche ou que tu veux éviter des notations à la Frenkel dans Géométrie pour l'élève professeur telle que $\Theta$
-
Bonjour Barry.Le programme parle bien d'une initiation :"- Comprendre et utiliser des notions élémentaires de probabilité.
- Calculer des probabilités dans des contextes familiers."avec comme commentaires :"La notion de probabilité est abordée à partir d’expérimentations qui permettent d’observer les fréquences des issues dans des situations familières (pièces de monnaie, dés, roues de loteries, urnes, etc.).
La notion de probabilité est utilisée pour modéliser des situations simples de la vie courante. Les situations étudiées concernent les expériences aléatoires à une ou à deux épreuves."Il y a déjà de quoi faire ... surtout sur les situations à deux épreuves. Par exemple répondre à la question : "Dans une loterie, vaut-il mieux être le premier ou le deuxième à prendre un billet ?".Cordialement.NB. Ce programme est totalement flou (quelles notions sont élémentaires ?? et les "contextes familiers" sont décidés comment ?), donc on peut faire pas mal de choses, ou très peu. -
Pour les deux épreuves, le fait qu’on multiplie les probabilités est aussi une sorte de « grand pas », je trouve. La représentation en arbre également.
-
Bonjour Stfj.Le programme n'est pas une introduction à la théorie moderne des probabilités, mais seulement à la notion intuitive de probabilité. La notion de "une chance sur 100" et un début de mathématisation (dont se sont contenté les mathématiciens jusque vers 1950 pour certains).Cordialement.
-
@Barry : je n'ai jamais trouvé pertinente l'introduction des probas au collège. Et je continue à trouver cette introduction déplacée. Mais comme c'est le programme... Témoins les questions navrantes au brevet des collèges : en gros, dans une urne, il y a 2 boules blanches et une rouge. Quelle est la proba d'obtenir une blanche? C'est comme scratch, un programme de code créé pour des enfants de 8 ans dont nombre d'élèves de 3è se montrent incapables d'appliquer ne serait-ce que les bases. C'est un jugement objectif, il suffit de regarder les résultats au brevet sur les ex scratch. Je fais partie d'une génération (je suis né en 1970) qui a découvert les probabilités en L3("licence de mathématiques" à l 'époque). En TC, il y avait juste du dénombrement en gros; en classes prépa pas de probas à la fin des années 80. J'ai donc découvert les probabilités via le cours de théorie de la mesure de L3 avec un enseignant plus soucieux de rigueur mathématique que d'applications de la théorie de la mesure à la théorie des probabilités . Et j'ai a d o r é son cours...
-
Pas de souci, Barry, car de mon point de vue se demander « à quoi ça sert » n’est pas pertinent.
J’ai tout de même répondu à ta question que je n’ai pas trouvé ridicule.stfj, pire ! Ils mettent deux boules rouges et deux boules blanches. Comme ça, « deux couleurs DONC une chance sur deux ». C’est désastreux. -
Lancer de pile ou face, lancer d'un de... Entre autres.
-
Au fait, Claude Deschamps est-il bien le professeur de mathématiques spéciales $MP^*$ au lycée Louis-le-Grand, le $D$ de Ramis-Deschamps-Odoux ? Ou est-ce un homonyme ?
-
@gerard0 : bonjour. Tu écris : "Le programme est une introduction à la notion intuitive de probabilité. La notion de "une chance sur 100".
J'ai enseigné de nombreuses années au collège les probabilités. Je les ai même enseignées un peu moins longtemps au lycée. Je ne sais pas ce qu'est la "notion intuitive de probabilité". Par contre, je sais ce qu'est une probabilité sur un ensemble fini. Qu'est-ce que je réponds à un élève intelligent( et j'en ai eus beaucoup) qui vient me voir à la fin du cours et me dit : "monsieur, je n'ai pas bien compris ce qu'est une probabilité. Qui fixe les probabilités ? Combien de fois doit-on lancer une pièce pour être sûr qu'elle tombe une fois sur deux sur pile ? Combien a-t-on dû faire exploser de bombes atomiques pour valider les systèmes probabilistes associés? Si j'ai un trou le jour du brevet, dois-je répéter l'expérience avec des bouts de papier dans ma trousse pendant un quart d'heure pour retrouver telle ou telle probabilité, ou pendant une demi-heure ?...C'est quoi une probabilité, monsieur ?"Cordialement. -
Stfj,
tu as de la chance, tu as eu un prof qui parlait de probas en L3, et tu as fait une TC qui parlait de probas sur des univers finis. Moi je n'ai pas eu de cours de probas, et l'UV qui parlait des théorèmes nécessaires en probas s'appelait "calcul intégral", avec un prof formé par la génération Bourbaki pour qui les probas n'étaient pas des maths. Donc j'ai tout appris par moi-même.Fais très attention, tu préfères les présentations plus théoriques, soigneusement étayées et rigoureuses. Mais la plupart de tes élèves ne sont pas ainsi. Tu vas former quelques futurs "très bons en maths", mais tu ne mesureras pas les dégâts sur ceux qui sont plus concrets. Faire de la mathématique une science purement abstraite dessert la discipline, c'est déjà ce qui l'a desservie dans les années 70-80, qui a amené la "dé-mathématisation" des programmes de physique du secondaire, qui a fait rejeter les MC de maths pour les cours de maths/probas/stats dans les facs de science éco-gestion.Cordialement. -
Bonjour, les questions des élèves dépendent fortement de la manière dont est présentée une notion. S'ils se demandent ce qu'est une probabilité, c'est justement qu'il y a eu un loupé dans ta présentation. Normalement en voyant l'usage qui en est fait, la question sur ce que c'est n'a plus de raison d'être.
La notion intuitive de probabilités, c'est, pour moi, la quantification des chances qu'à un évènement de se réaliser. Cette quantification peut s'obtenir de manière théorique en identifiant les évènements élémentaires (et en supposant qu'ils ont autant de chance de se produire en l'absence d'information particulière). Elle peut aussi s'estimer expérimentalement par la fréquence passée de tel ou tel événement. Tout cela ne nécessite aucun formalisme. Je n'ai rien contre la définition un peu théorique d'une probabilité comme une application mais ce qui me paraît indispensable, c'est d'avoir intégré la notion intuitive qui est utile dans la vie de tous les jours. D'accord avec Dom sur l'enjeu sociétal.In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
Même Poincaré jugeait la notion de probabilité compliquée (je n'arrive pas à retrouver sa phrase célèbre à ce sujet). Et pourtant il ne m'a pas eu comme prof. Je n'ai pas la prétention de connaître beaucoup de mathématiques mais au moins celles que j'enseigne. Contrairement à Poincaré, je sais ce qu'est une probabilité. Disons que j'ai Poincaré comme élève en 3è (vu le talent de certains de mes élèves, c'est tout-à-fait envisageable.) Il vient me voir à la fin du cours et me dit : "je ne comprends rien à votre bla-bla. Qu'est-ce qu'une probabilité ?" J'avoue que je répondrais volontiers alors à Henri.
-
C'est exagéré, la notion intuitive de probabilités est très simple je trouve. Le formalisme est compliqué, ça tombe bien, il ne sert à rien avant le post-bac (et encore même à ce moment là je suis souvent dubitative). Solution KISS (Keep It Simple Student), aucun élève ne dira qu'il ne comprend rien à mon bla bla et tous s'en moquent d'avoir une définition au sens où tu l'entends. Attention à ne pas prendre tes désirs pour la réalité et à vraiment t'intéresser à la demande des élèves, pas à celle que tu aimerais avoir.
PS. J'ai aussi de très bons élèves venant de très bons lycéesIn mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
Je réfléchis à ma bataille navale. On ne peut pas a priori tenir compte des coups déjà joués puisqu'on ne sait pas combien il y en a eus. Il y a alors une probabilité de $p(A)=\frac{26}{100}$ pour $A$:"toucher un bateau" et donc $p(\overline{A})=1-0.26=0.74$. On peut imaginer comme dans le Belin qu'on est au 6è tour. Quelle est alors la proba de toucher ? C'est le tout dernier ex (ex 50) du Belin. Je trouve que cela nécessite peu de réflexions de la part des élèves et a peu d'intérêt pour leur formation mathématique. Et pourtant cela apparaît ici comme un lien avec les aires et donc la théorie de la mesure: j'espérais un peu dans cet exercice et il me fait l'effet d'un pétard mouillé.

-
Q : C’est quoi une probabilité ?
R : Une application qui …
Q : C’est quoi une application ?
R : C’est un ensemble qui …
Q : C’est quoi un ensemble ?
Toutes les discussions peuvent venir à cette même fin… (si c’en est une…)
En ce sens, savoir ce qu’est une probabilité ne permet pas de résoudre un exercice de collège qui porte sur la notion de probabilité.Je pense qu’il faut donner quelque chose dans le cours mais qu’il faut surtout savoir utiliser le vocabulaire et répondre aux questions à la sortie du cours MIEUX que quand on y est entré.Certes c’est le B.A. BA. -
Je ne vois pas une exploitation pertinente de cette bataille navale. Je me méfie des situations où il faut expliquer les règles d’un jeu pendant 30 minutes et où la solution d’un exercice se fait ensuite en moins 5 minutes. Ce sont 30 minutes de perdues sauf si l’on relance l’exercice à chaque heure ensuite.Un peu comme quand on parle « d’un jeu classique de 32 cartes » et que dans la classe plus personne ne sait que les couleurs sont au nombre de quatre, que rouge et noir ne sont pas parmi les couleurs et que « valet » ne dit rien à personne.Dans certains bahuts, on ne joue plus (ou pas) avec ces jeux de cartes depuis au moins deux générations, alors, il faut trouver un autre outil (j’allais dire « culturel » mais en fait ce n’est pas nécessaire).Même le jeu de UNO est inexploitable dans un autre cercle de probabilité car personne ne connaît la répartition des cartes dans un jeu. Bref. On oublie les cartes, sauf dans les zones rares où ça se pratique encore.
-
C'est surtout risqué, un élève intelligent va forcément te faire remarquer qu'une fois qu'on a touché, cela change la probabilité des cases adjacentes car on sait que le bateau se prolonge sur l'une des cases adjacentes. La proba ne sera alors plus la même sur toutes les cases.
Ne sois pas déçu, la théorie de la mesure en probabilités n'a pas vraiment d'intérêt ni pour le collège ni pour le lycée et de toute façon, l'exercice serait le même avec des points à l'intersection d'un quadrillage, le lien avec les aires est faible, on est en discret.
Si tu y tiens vraiment, je te suggère de partir plutôt sur un jeu de fléchettes avec une distribution uniforme sur la cible. S'ils savent calculer l'aire d'un disque, c'est jouable.In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
@Dom : tu as tout-à-fait raison dans tes Q-R. C'est la raison pour laquelle je plaide pour la réintroduction d'un minimum de théorie des ensembles naïve dès la 6è. Vus les classements actuels des élèves français en maths, plus grand monde n'aura de leçon définitive à me donner sur ce qu'il est souhaitable de faire ou pas. Alors je prends les devants et je propose en réclamant bien-sûr un regard critique. Il est pour moi évident qu'avoir les mêmes notations pour la géométrie élémendaire, les aires, les dénombrements simples, les probabilités, réduirait le travail des élèves tout en leur permettant de réfléchir aux liens étroits entre toutes ces notions présentées de façon éparse comme des cheveux sur la soupe. $$\text{aire}(A\cup B )=\text{aire}(A)+\text{aire}(B ) \text{ si } A\cap B=\varnothing$$$$\text{Card}(A\cup B )=\text{Card}A+\text{Card}B\text{ si } A\cap B=\varnothing$$$$p(A\cup B )=pA+pB \text{ si } A\cap B=\varnothing$$
Avec des dessins en couleurs comme quand j'avais 8 ans, tout le monde sait que ça passe comme une lettre à la poste. "De ce paradis, nul ne pourra nous chasser". Il est vrai qu'Hilbert ne songeait pas aux enseignants du secondaire. Vue la formation des professeurs de lycée et collège, cela relève de la schizophrénie : tu as toutes les billes pour expliquer aux élèves mais tu n'as pas le droit de jouer avec sous prétexte que tes collègues ont été évidemment dépassés par la massification scolaire dans les années 70...
sous prétexte que tes collègues ont été évidemment dépassés par la massification scolaire dans les années 70... -
Moi aussi j'aimerais bien qu'on m'explique ce qu'est la bonne notion intuitive d'une probabilité mais je vais m'abstenir vu que ça n'avait pas été très apprécié la dernière fois que j'en ai discuté.
Qu'est-ce qui fait qu'une pièce tombe une fois sur deux sur pile et une fois sur deux sur face ? Ben rien, c'est faux sauf en moyenne quand on fait une infinité de lancers, ce qui m'est impossible de faire... . Tout ce qu'on peut faire, c'est induire avec la loi bêta le paramètre $p= \frac{1}{2}$ avec une certaine certitude que l'on contrôle (et c'est ce contrôle de l'incertitude qui me paraît le plus proche d'une notion intuitive des probas).
Mais pour l'expliquer à des 3e... on fait avec les mains !
Le mieux, c'est de leur faire accepter le principe suivant mentionné par Vassilia : "A priori, les évènements élémentaires ont autant de chances de se produire (sont équiprobables)". C'est précisément en réalisant des expériences scientifiques sur le résultat d'un lancer de dé par exemple qu'on finit par accepter que c'est comme ça, c'est magique. Et après, on vient dire que les maths, ce n'est pas de la science ...
-
Hum… attention tout de même avec « les événements élémentaires ont autant de chance ».C’est faux sauf à savoir définir ce qu’est un événement élémentaire…
Dans les exemples suivants, est-ce équiprobable ?
1) Il pleut/il ne pleut pas, à Paris, à 10h00 le 14 juillet
2) Un référendum (au choix)
3) Je jette non pas un dé, mais une boîte parallélépipédique non cubique…
quels sont lesdits « événements élémentaires » ?
4) Je tourne la roue suivante
-
Bonjour stfj
Les dés à trois faces, cela existe (Wiki...) mais c'est quand même rare !Et pourquoi pas les faire jouer avec des tirages (successifs avec ou sans remise) de 2 cartons (parmi 5, par exemple...) indiscernables numérotés de 1 à 5, portant la couleur rouge (3 cartons 1/2/3) et verte (n°4/5). Et à toi de varier les questions.Pratique et pas cher.
Bon, l'intérêt n'est pas fantastique, certes...
Cordialement.
PG -
Bonjour @PG : super idée, merci. Cela fait une heure que je joue machinalement avec mes cartons, c'est comme une boule anti-stress et en plus on apprend...(Ce qui m'intéresse dans le dé à trois faces, c'est : $U=\{1,2,3\},\ \mathcal{P}(U)=\{\varnothing,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\}, U\},\ p=0,\frac13,\frac23,1$ : une description totale de la probabilité : peu intéressante pour une pièce de monnaie, fastidieuse et inutile pour un dé à $6$ faces. En outre, si "$S$ : obtenir un nombre pair" et "$E$ : obtenir un nombre impair" $p(S)\neq p(E)$)

-
J’ai $\Omega=\{\text{coeur},\text{carreau},\text{pique},\text{trèfle}\} \times\{10, \text{valet},\text{dame},\text{roi}, \text{as}\}$.
Un événement élémentaire, c’est une carte du jeu, c’est-à-dire un élément de ce produit cartésien.
Ainsi l’évènement « Tirer un as » est la réunion de quatre événements élémentaires équiprobables: (cœur,as), (pique,as), (trèfle,as), (carreau,as).
La probabilité de l’événement « Tirer un as » est donc la somme des probabilités des événements élémentaires: $1/5$.
C’est la bonne vieille probabilité intuitive chère à Poincaré ! -
C’est presque à mourrir de rire de parler d’intuition quand on parle d’un produit cartésien, de réunion, de somme etc.
-
C'est un homonyme, c'est l'épouse de Didier !stfj a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2404970/#Comment_2404970[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]
Karl Tremblay 1976-2023, je t'appréciais tellement. -
Ben, ce n’est pas si « à mourir de rire » que ça ! Un élève de sixième peut comprendre le produit cartésien.
Le problème avec la probabilité dite « intuitive », c’est qu’elle n’évite pas les ambiguïtés. Si on se contente de jeux de dés ou de cartes, ça va. Après, intervient l’axiomatique de Kolmogorov. Mais on ne va tout de même pas enseigner au collège, les mesures de probabilités sur une $\sigma$-algèbre ! Le prof va se retrouver au tribunal pour maltraitante pédagogique. -
Oui, oui. Je veux dire que la modélisation fera peur (les notations et le vocabulaire font peur). Et que pour décrire l’intuition « ordinaire », sortir un dictionnaire nouveau et des symboles nouveaux, c’est amusant.
-
Biguine :si, pourquoi pas ? 😊
-
Pour moi le cours peut être chronologiquement construit comme ça :
1) univers, issues, événements élémentaires, événements, notations avec accolades
2) loi de probabilité sur un univers : on la « définie » en la donnant à chaque fois en mettant des événements élémentaires de probabilités non forcément égales.•On a les exercices classiques où l’on donne $n-1$ probabilités et où il faut trouver celle qui manque.•D’autres où « non, ce n’est pas une loi de probabilité car ça dépasse 1 ».•D’autres encore où l’on doit chercher les probabilités selon certaines contraintes (les pairs valent le double des impairs, les probabilités sont égales, les probabilités sont proportionnels aux faces, etc.)3) on passe aux événements : on dit (definition) que la probabilité d’un événement est la somme des probas élémentaires de chaque issue qu’il contient.4) à la toute fin on propose les exercices (insupportables mais ils existent… partout) où l’élève doit deviner l‘équiprobabilité.De manière transversale, la représentation en tableau (de valeurs) ou en arbre peut être faite dès le début.La partie « expérience à deux épreuves » peut être vue un peu plus tard, une fois que tout a bien mariné dans la tête. -
L'indépendance des expériences aléatoires : avant ou après le travail en autonomie ?
-
🤣
-
Je me suis livré à l'exercice proposé par @PG. J'ai fait 11 tirages de deux cartons avec remise : sur le tableur, chacun des tirages $(A,B)$ est numéroté de $1$ à $11$:
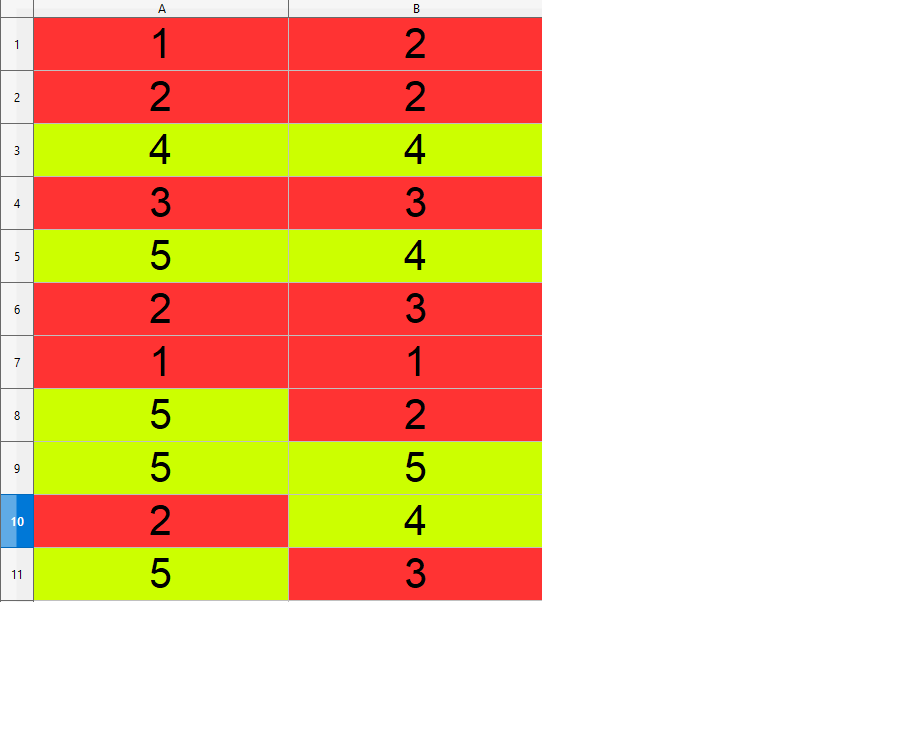
Si l'on considère les tirages indépendamment du fait qu'ils sont associés deux par deux, les statistiques traduisent d'une part à peu près l'équiprobabilité d'obtenir $1,2,3,4$ ou $5$; d'autre part, on obtient une probabilité $p(Rouge)=\frac{13}{22}\approx 0.59$, ce qui est absolument remarquable puisque $p(Rouge)=\frac35=0.6$. C'est une superbe activité susceptible de nombreux développements intéressants. Merci à nouveau. -
Les probas du collège (finitistes) consistent surtout à faire fonctionner l'idée qu'une probabilité est une proportion (nombre de cas favorables/ nombre de cas possibles). Il s'agit de faire du dénombrement et donc de manipuler des cardinaux d'ensemble finis.
Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
Du dénombrement ?Oui mais dans un cadre très naïf, sans technique. Sans les p-listes, combinaisons, arrangements…
-
Dom
Je n'ai aucun respect pour la censure académique qui a voulu faire disparaître les arrangements du paysage intellectuel de toute la tranche d'âge des moins de 20 ans. Je décris ce qui se passe ci-dessous.1°) Arrangements. Etant donnés deux ensembles $X$ et $Y$, on notera ci-dessous $\mathfrak I(X,Y)$ l'ensemble des injections de $X$ dans $Y$.On montre par récurrence sur $p\in \N$ la propriété suivante: pour tout entier $n$, $n > p$, ou pour tous ensembles $X,Y$ tels que $card(X)=p$ et $card (Y) = n$, le nombre $A^p_n$ d'éléments de $I(X,Y)$ est égal à $\prod_{i=1}^p (n-i+1)$. En effet, lorsque $p=0$, ce produit vaut $1$ et l'ensemble des injections de $\emptyset$ dans $Z$ est égal à $\{\emptyset\}$ pour tout $Z$. Supposons maintenant que la propriété soit vraie en $p\in \N$. Soit $n\in \N$. Si $p+1>n$ le résultat est évident. Sinon, $p+1\leq n$ et donc $p \leq n-1$. Soient $X$ un ensemble à $p+1$ éléments, $Y$ un ensemble à $n$ éléments, $a\in X$, $b\in Y$. On note $E_{a,b}$ l'ensemble $\{f\in \mathfrak I (X,Y) \mid f(a) = b\}$. Alors pour toute $g\in \mathfrak I(X\backslash \{a\},Y\backslash \{b\})$, il existe un seul élément $f$ de $E_{a,b}$ tel que $f|_{X\backslash \{a\}} = g$. Donc $E_{a,b}$ et $\mathfrak I(X\backslash \{a\},Y\backslash \{b\})$ sont en bijection et comme (hypothèse de récurrence) $\mathfrak I(X\backslash \{a\},Y\backslash \{b\})$ possède $\prod_{i=1}^p (n-1+1-i) = \prod_{i=1}^p (n+1 - (i+1)) = \prod_{i=2}^{p+1} (n-i+1)$ éléments, il en va de même de $E_{a,b}$. On conclut en remarquant que $\mathfrak I(X,Y)$ est la réunion disjointe de la famille $(E_{a,b})_{b\in Y}$, qui possède $n$ éléments, tous ayant $\prod_{i=2}^{p+1} (n-i+1)$ éléments et donc $\mathfrak I(X,Y)$ possède $n\times \prod_{i=2}^{p+1} (n-i + 1) = \prod_{i=1}^{p+1} (n-i+1)$ éléments ce qui est le résultat voulu.
Le nombre d'injections d'un ensemble à $p$ éléments dans un ensemble à $n$ éléments s'appelait autrefois nombre d'arrangements et se notait $A^p_n$. L'égalité $A^p_n = \prod_{i=1}^p (n-i+1) = n(n-1) ... (n-p+1) = \frac{n!}{(n-p)!}$ est démontrée par le raisonnement précédent, qui est la formalisation de l'argument "il y a $n$ façon de choisir le premier élément dans $Y$, puis $n-1$ façons de choisir le deuxième puis $n-2$ façon de choisir le troisième, etc... enfin $n-p+1$ façons de choisir le $p$-ième".Lorsque $n=p$, on retrouve le nombre de bijections d'un ensemble à $n$ éléments dans un autre qui est $\frac{n!}{0!} = n!$.2°) Combinaisons. Soient à nouveau $p,n$ deux entiers naturels avec $p\leq n$. Soit $X:=\{1,...,p\}$. Soit $Y$ un ensemble à $n$ éléments. Soit $\mathfrak P_p(Y)$ l'ensemble de toutes les parties de $Y$ qui ont exactement $p$ éléments. Alors pour tout $Z\in \mathfrak P_p(Y)$, $ \mathfrak I(X,Z)$ est l'ensemble des injections (donc bijections) d'un ensemble à $p$ éléments dans un autre et possède $p!$ éléments (voir ci-dessus). Il est clair que $\mathfrak I(X,Z)$ est inclus dans $\mathfrak I(X,Y)$. D'autre part pour tout $f\in \mathfrak I(X,Y)$, l'image $im(f)$ de $f$ appartient à $\mathfrak P_p(Y)$ et $f$ appartient à $\mathfrak I(X,im(f))$. Enfin, si $Z,T$ sont des éléments distincts de $\mathfrak P_p(Y)$, il est clair que l'intersection de $\mathfrak I(X,Z)$ et de $\mathfrak I(X,T)$ est égale à $\mathfrak I(X,Z\cap T)$ et que ce dernier ensemble est vide puisque $Z\cap T$ possède strictement moins d'éléments que $Z$ (qui a $p$ éléments) et donc aucune fonction de $X$ dans $Z\cap T$ ne peut être injective.Ainsi, $\mathfrak I(X,Y)$ (qui a $A^p_n$ éléments) est la réunion disjointe des ensembles à $p!$ éléments $\mathfrak I(X,Z)$ lorsque $Z$ parcourt $\mathfrak P_p(Y)$. Il en résulte que $\mathfrak P_p(Y)$ est un ensemble fini à $\frac{A^p_n}{p!} = \frac{n!}{(n-p)!p!}$ éléments. Le nombre de parties à $p$ éléments d'un ensemble à $n$ éléments, qui vaut donc $\frac{n!}{(n-p)!p!}$ s'appelait autrefois "nombre de combinaisons" et se notait $C^p_n$ mais on emploie aujourd'hui (par imitation des anglo-saxons) la notation $\binom{n}{p}$ (attention au changement de position de $n$ et de $p$) pour le désigner et on utilise aussi l'expression "$p$ parmi $n$".Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
stfj a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2404970/#Comment_2404970[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]C'est lui; voir https://www.idref.fr/026826623Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$.
-
C'est bien vrai ça, rendre incompréhensible des notions normalement compréhensibles par un lycéen est beaucoup plus subtil que de censurer mais curieusement, cela ne m'inspire pas beaucoup plus de respect.
Est un argument tout à fait suffisant (comme quoi c'est possible). Pour combinaisons, comme on passe aux nombres de sous-ensembles, il faut diviser par le nombre de manières d'ordonner $p$ éléments et on répète l'argument précédent pour la façon de choisir les places (et voilà on met déjà en pratique ce que l'on vient d'apprendre)."il y a $n$ façon de choisir le premier élément dans $Y$, puis $n-1$ façons de choisir le deuxième puis $n-2$ façon de choisir le troisième, etc... enfin $n-p+1$ façons de choisir le $p$-ième".
Dans ces conditions, on peut effectivement aborder ces notions très tôt pour leur faire faire des exercices. Inconvénient de la méthode : elle fâche le monde académique qui tient tant à rendre ces notions incompréhensibles mais est-ce bien grave ? Pas tant que ça car en réalité ils n'ont aucun pouvoir de censure.In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
Ma politique est de livrer en priorité l'information; la pédagogie (whatever that means) est en bonus.
Prends ton logiciel de vérification de preuve préféré et essaie de le rentrer dedans... Il y a des gens qui se demandent (à bon droit) pourquoi les arguments dits "heuristiques" ou "avec les mains" de la combinatoire peuvent se formaliser c'est-à-dire se mettre au propre en mathématiques.Vassillia a dit :
Est un argument tout à fait suffisant (comme quoi c'est possible)."il y a $n$ façon de choisir le premier élément dans $Y$, puis $n-1$ façons de choisir le deuxième puis $n-2$ façon de choisir le troisième, etc... enfin $n-p+1$ façons de choisir le $p$-ième".Mon message précédent s'adresse aussi à eux.
On garde les notations de mon message plus haut. Soient $p\leq n$ des entiers et $Y$ un ensemble à $n$ éléments; soit $X:=\{1,...,p\}$. Etant données $f,g\in \mathfrak I(X,Y)$ on abrège par "$f \sim g$" l'énoncé "il existe une bijection $\sigma$ de $\{1,...,p\}$ dans lui-même tel que $f \circ \sigma = g$." Il ne t'auras pas échappé que $\sim$ est une relation d'équivalence sur $\mathfrak I (X,Y)$ sont les classes sont exactement les $\mathfrak I(X,Z)$ où $Z$ parcourt $\mathfrak P_p(Y)$ puisque pour tous $f,g\in \mathfrak I(X,Y)$, $f\sim g$ si et seulement si $im(f)=im(g)$. Ainsi l'application $f\mapsto im(f)$ de $\mathfrak I(X,Y)$ dans $\mathfrak P_p(Y)$ induit par passage au quotient une bijection entre $\mathfrak I(X,Y) /\sim$ et $\mathfrak P_p(Y)$. Les éléments de $\mathfrak I(X,Y)/\sim$ sont les arrangements de $p$ éléments de $n$ "pour lesquels l'ordre ne compte pas". La façon dont le texte précédent a été rédigé était pour éviter cette digression. Bien sûr les lecteurs sont invités à raccourcir ces preuves si possible.Vassillia a dit :Pour combinaisons, comme on passe aux nombres de sous-ensembles, il faut diviser par le nombre de manières d'ordonner p éléments et on répète l'argument précédent pour la façon de choisir les placesUne fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
Ah oui, alors dis moi dans quel logiciel de vérification de preuve, je peux copier-coller ton texte ? Promis j'essaye.
In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
Normalement mizar est ensembliste donc ie truc doit pouvoir se traduire directement dans la syntaxe du langage (Coq non, d'ailleurs la combinatoire est une vraie corvée dedans et le résultat sera plus long et carrément reformulé). En tout cas le coup de "on fait ceci et cela avec les mains"... bon courage avec ça!!
Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
Ben alors, je suis déçue, s'il faut traduire, c'est que ta version n'est pas non plus compatible avec un logiciel de vérification de preuve en l'état actuel des choses. Du coup elle est pour qui ? Un ordinateur (apparemment non), les élèves de moins de 20 ans (clairement non), les profs de maths (ils connaissent déjà ces notions).Je n'ai rien contre le fait que tu t'amuses à formaliser des arguments qui passent très bien avec les mains, peut-être que cela intéresse du monde (ou peut-être pas) mais tu exagères à faire croire qu'il y a une censure académique. Il y a des notions qui sont difficiles à faire passer à des élèves et le formalisme n'aide pas toujours, il peut même desservir. En l’occurrence, on peut très bien faire du dénombrement au lycée voir peut-être même au collège en utilisant les combinaisons et les permutations si on se donne la peine de rendre ces notions compréhensibles pour ce niveau et je trouve dommage que tu ne fasses pas cet effort dans un fil dont le titre part de collégiens. Le pire, c'est que je suis sûre que tu saurais faire si tu voulais et tu pourrais apporter aux profs du secondaire une manière de présenter les choses rigoureuse sans sacrifier à la compréhension (j'ai relu vraiment ton texte et il est compréhensible disons après quelques semestres de licence)In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu)
-
Il faut toujours traduire pour utiliser un ordinateur, ça s'appelle coder. Les maths en prose précise sont essentiellement du pseudo-code. Mais peut-être que tu es contre le pseudo-code. Quant aux étudiants de moins de 20 ans, certains (nés entre octobre et décembre inclus) fêtent leurs 20 ans en école et on largement assimilé ça en maths sup. Pourquoi ces généralités fausses? Il y a eu des ensembles au collège à une époqueVassillia a dit :Ben alors, je suis déçue, s'il faut traduire, c'est que ta version n'est pas non plus compatible avec un logiciel de vérification de preuve en l'état actuel des choses. Du coup elle est pour qui ? Un ordinateur (apparemment non), les étudiants de moins de 20 ans (clairement non), les profs de maths (ils connaissent déjà ces notions). . Et ça devrait continuer parce qu'en l'espèce la combinatoire (comprenez ici: le dénombrement) est une discipline en fait profondément ensembliste (il y a de gros usages d'extensionnalité sous-jacents: comme il n'y a pas ça dans COQ qui est une théorie des types, on est déjà en difficulté rien que pour juste exprimer une propriété telle que "card (bool^bool) = 4" avec bool = {true,false}).
. Et ça devrait continuer parce qu'en l'espèce la combinatoire (comprenez ici: le dénombrement) est une discipline en fait profondément ensembliste (il y a de gros usages d'extensionnalité sous-jacents: comme il n'y a pas ça dans COQ qui est une théorie des types, on est déjà en difficulté rien que pour juste exprimer une propriété telle que "card (bool^bool) = 4" avec bool = {true,false}).
Pour ce qui est des profs, quand tu es amené à en aider certains... Ca dépend des gens je dirais, c'est pourquoi je suis favorable au fait de diffuser ces notions le plus largement possible.
Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
Je ne suis contre rien du tout tant que c'est utile ou que cela facilite la compréhension d'une notion.
Du coup, je suis pour une approche très élémentaire des ensembles au collège, les diagrammes que j’appelle patates (aussi appelé diagramme de Venn pour faire plus savant) me paraissent très bien pour ce niveau. Je sais, tu risques de hurler que ce n'est pas assez formel mais tant pis, au moins, ils arriveront à sortir les formules basiques avec union et intersection.
In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
@Foys. On pourrait aussi considérer que le raisonnement"il y a n façon de choisir le premier élément dans Y, puis n−1 façons de choisir le deuxième puis n−2 façon de choisir le troisième, etc... enfin n−p+1 façons de choisir le p-ième"est également un pseudo-code.En tout cas, de nombreuses preuves de dénombrement sont rédigées avec ce type de pseudo-code sans que ça ne dérange personne.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.8K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 771 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres




