Hyperplan

OShine

Bonsoir,

Je bloque à la question 2.

1) $\ker (\phi)$ est un sous-espace vectoriel de $E$.
Si on considère la forme linéaire $\phi : E \longrightarrow \R$, comme $\phi$ est non nulle, $Im(\phi) \ne \{0 \}$ donc $\dim Im(\phi)=1$. 
D'après le théorème du rang : $\dim \ker (\phi) + rg(\phi)=n$. 
Finalement $\boxed{\dim \ker (\phi)=n-1}$.
$\ker(\phi)$ est bien un hyperplan.

raoul.S

Tu prends un supplémentaire de $H$ et tu définis $\phi$ sur $H$ puis sur le supplémentaire que tu as choisi...

OShine

Soit $x \in E$ tel que $x \notin H$. On a :  $E=H \oplus \R x$. Le reste je n'ai pas compris ce qu'il faut faire.

Alain24

OShine
Si tu choisis  $\phi$ telle que $\forall h\in H,\forall \lambda\in \mathbb{R},\phi(h+\lambda x)=\lambda$ que valent $Im(\phi)$ et $\ker(\phi)$ ?

stfj

@OShine : comme son nom l'indique, la notion d' hyperplan est la généralisation de la notion de plan passant par $(0,0,0)$ dans $\mathbb R ^3$, l' "espace". Par exemple, le plan (sous-espace vectoriel de dimension $3-1$) d'équation $z=0$ est un hyperplan de $\mathbb R ^3$. Pour t'aider, le mieux me semble-t-il, est même de considérer un hyperplan de $\mathbb R ^2$, ie, en se référant à la définition fournie par ton exercice, un sous-espace vectoriel de dimension $2-1$, ie une droite de $\mathbb R ^2$ passant par $(0,0)$. Prenons un exemple simple et considérons la droite $H$ d'équation $y=0$. Alors, comme @raoul.S te propose de le faire, tu prends un supplémentaire $H'$ de $H$, par exemple la droite $H'$ d'équation $x=0$. Tout point $(x,y) $de $E=\mathbb R ^2$ s'écrit de façon unique $(x,0)+(0,y)=(x,0)+y(0,1)$. [C'est ce que tu as écrit dans ton deuxième commentaire $E=H\oplus \mathbb R a$, avec $a=(0,1)\notin H$] L'idée est alors de définir $\phi$ de $E$ dans $\mathbb R$ par $$\phi((x,y))=y, \text{ pour tout } (x,y)\in E$$ et, comme les trois petits points de @raoul.S te l'indiquent, de vérifier que (1)$\phi \in \mathcal{L}(E,\mathbb R)$ (2)$H:y=0$ est bien égal à Ker$ \phi$. Evidemment un dessin sera le bienvenu.
(remarque : la véritable généralisation des plans de $\mathbb R ^3$, c'est les hyperplans affines, ie les parties d'un espace vectoriel réel $E$- pas forcément de dimension finie - de la forme $a+H$, où $a\in E$ et $H$ désigne un hyperplan vectoriel de $E$, autrement dit un hyperplan passant par $0$. La démonstration faite ici pour les hyperplans vectoriels s'étend, même si on remplace $\mathbb R$ par un corps commutatif quelconque $K$. Elle est même plus limpide, dégagée d'hypothèses inutiles. Bref, comme souvent en algèbre linéaire si tu comprends ce qui se passe en dimension $2$ ou $3$, t'as -presque- tout compris : ici, en dimension $2$, cela te dit que les droites de $\mathbb R^2$ sont les parties du plan d'équations $ax+by=c$, avec $a$ et $b$ réels non tous deux nuls et $c\in \mathbb R$; un hyperplan de $\mathbb R^4$ ou de $\mathbb C^4$ est d'équation $ax+by+cz+dt=e$; ... ce qui peut servir Est-ce que mes explications t'ont aidé ?

OShine

Merci pour votre aide, je pense avoir compris.

@stfj c'est plus facile à comprendre avec la dimension 2 !

2) Soit $a \in E \backslash H$. Alors on peut écrire $E=H  \oplus a \R$.
Soit $x \in E$. Alors il existe un unique couple, $(y,z) \in H \times a \R$ tel que $x=y+z$.
On définit $\phi : E \longrightarrow \R$ tel que $\phi(x)=\phi(y+z)=z$. C'est évidemment une forme linéaire de $E$ sur $\R$.
On a $x \in \ker( \phi) \iff \phi(x)=0 \iff z=0 \iff x=y \iff x \in H$.

Il existe bien une forme linéaire $\phi$ tel que $\boxed{\ker (\phi)=H}$.

stfj

Soit $x\in E$. Alors il existe un unique couple $(y,z)\in H\times \mathbb R $ tel que $x=y+z a$
On définit $\phi: E\to \mathbb R$ par $\phi(x)=\phi(y+z a)=z$...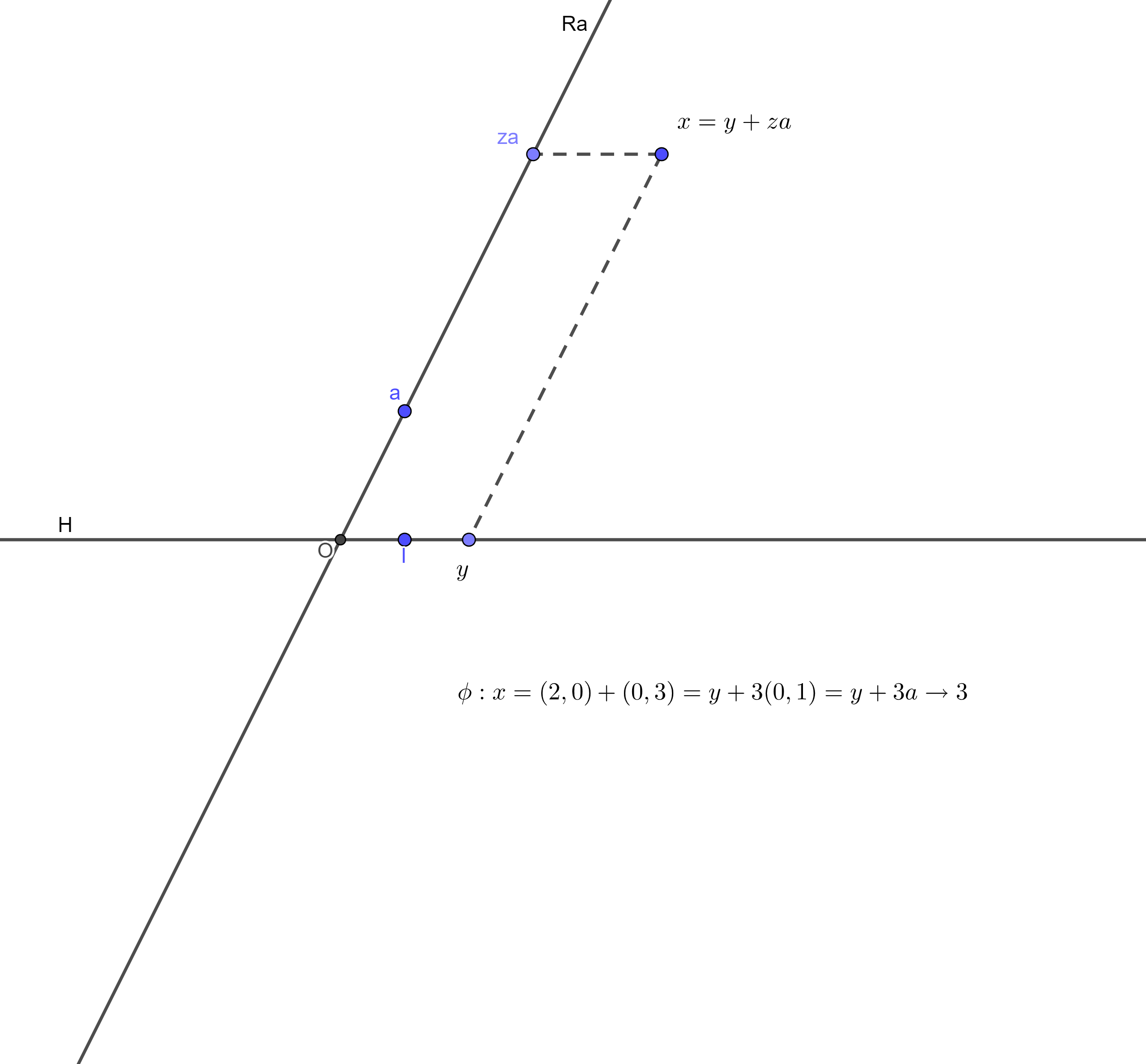

OShine

@stfj
Merci beaucoup, dessin très clair, je me rends compte que j'ai fait une erreur, car $a$ n'est pas réel, dans ton exemple c'est un point de $\R^2$.
Je ne peux pas prendre l'élément de $a \R$ mais je dois l'écrire $a z$ avec $z$ réel et prendre $\phi(x)=z$.

stfj

@OShine : c'est cela. Tu as parfaitement compris. Au passage pour un espace vectoriel réel, cela explique qu'un hyperplan sépare l'espace en la partition $\{f(x)>0, f(x)=0, f(x)<0\}$ : demi-espaces ouverts déterminés par $H$, comme une feuille de papier sépare l'espace et un point sur une droite sépare celle-ci en deux demi-droites.

OShine

D'accord ! Je n'avais jamais entendu parlé de partition dans l'espace.
3) Je ne trouve pas d'idée pour cette question, je ne vois pas d'où sort le $1$.

stfj

Si tu reprends la définition de $\phi$ donnée plus haut, que vaut $\phi(a)=\phi(0+1a)$?

OShine

$\phi(a)=1$ c'était tout bête.

NicoLeProf

En fait, c'est simple pour 2) : on prend $H$ de dimension $n-1$ . Alors $H$ admet un supplémentaire dans $E$ qui est une droite vectorielle que l'on notera $Vect(a)$ (en effet, il suffit de choisir un élément $a \neq 0$ de $E \setminus H$ tel que la famille $(h_1,...,h_{n-1}, a)$ soit libre dans $E$ où la famille $(h_1,...,h_{n-1})$ est une base de $H$. L'élément $a$ existe en vertu du théorème de la base incomplète).

Ensuite, on définit l'application linéaire $\phi : E \to \mathbb{R}$ telle que : pour tout $x \in H$, $\phi(x)=0$ et $\phi(a)=1$ par exemple (ou n'importe quel autre nombre réel non nul). L'application $\phi$ est entièrement déterminée car $H$ et $Vect(a)$ sont supplémentaires dans $E$ (car la famille $(h_1,...,h_{n-1}, a)$ est une base de $E$)  et il est immédiat que $H=\ker \phi$ .

NicoLeProf

@OShine, pour 3), c'est exactement ce que j'ai écrit ci-dessus : on a vu que $\ker \phi$ est un hyperplan de $E$. Notons $B=(e_1,...,e_{n-1})$ une base de $\ker \phi$ (qui est donc une famille libre dans $E$) . Comme $E$ est de dimension $n$, $E \neq \ker \phi$ et il existe un vecteur $w \in E \setminus \ker \phi$, $w \neq 0$ tel que la famille $(e_1,...,e_{n-1},w)$ est une base de $E$ (c'est une application du théorème de la base incomplète d'ailleurs !).

Alors, que peut-on dire de $\phi(w)$? Pourquoi? Conclure quant à la question posée !

Alain24

@OShine Pour aller plus loin, as-tu une intuition, sur ce que deviennent les propriétés que tu as démontré en dimension $2$ quand l'espace est de dimension infinie. 

Exprimé autrement: la géométrie du plan euclidien est reliée à l'algèbre linéaire sur le corps $\mathbb{R}$ en dimension $2$. En dimension infinie la géométrie des espaces affines euclidiens réels est reliée à l'algèbre linéaire sur le corps $\mathbb{R}$ par quel théorème?

De quels axiomes se sert-on pour obtenir ce théorème?

OShine

@NicoLeProf ok ça marche, tu redémontres le cours   

@Alain24 aucune idée.

4) Posons $H=\ker (\phi)=\ker(\psi)$. $H$ est un hyperplan d'après les premières questions.
On a $E=H \oplus v \R$.
On a $\phi(v) \ne 0$ et $\psi(v) \ne 0$ car $v \notin H$.
Définissons $h$ l'application linéaire définie par $h=\phi(v) \psi - \psi (v) \phi$.
$\forall x \in H$, $h(x)=0$ par définition et $\forall \lambda \in \R$ on a $h( \lambda v)= 0$
On en déduit que $h$ est nulle sur $E$.
Ainsi : $\phi(v) \psi = \psi(v) \phi$. Comme $\psi(v)=1$, cela donne $\psi = \psi(v) \phi$.

En posant $\lambda= \psi (v)$, on a bien $\boxed{\psi = \lambda \phi}$. 

NicoLeProf

Je ne vois pas en quoi je redémontre le cours, j'applique les définitions et propriétés de base des hyperplans c'est tout. La preuve du théorème de la base incomplète est bien plus difficile que ce que j'ai écrit. Vraiment OShine, apprends à te détacher du "cours" ! ^^'

Ta démonstration de $4$ est trop compliquée je trouve.

Il suffit de remarquer que $\phi(\lambda v)=\lambda \phi(v)=\lambda$ donc $\psi(v)=\lambda \phi(v)$ . Donc par linéarité, $\psi$ et $\lambda \phi$ coïncident sur $vect(v)$ et on montre immédiatement que $\psi$ et $\lambda \phi$ coïncident sur $H=\ker \phi=\ker \psi$ .

OShine

Le cours dit directement que si $H$ est un hyperplan et $a \notin H$ alors $E=H \oplus a \R$. 
Pourquoi reparler de base incomplète etc ? C'est une perte de temps.
Je vois ce résultat utilisé directement dans de nombreux corrigés de concours.

En effet, ta solution à 4 est plus rapide ! 

Bibix

De toute façon, le théorème de la base incomplète, c'est une évidence en dimension finie. Pas besoin de Zorn, ou d'AC, il suffit juste de remarquer que $a \notin H$ est forcément linéairement indépendant de toute base de $H$ car sinon $a$ serait dans $H$.

OShine

@Bibix
D'accord merci.

La question 5 semble plus difficile. Il m'aura fallu 45 minutes pour trouver une solution. Et encore je ne suis pas sûr que ce soit juste...
Mais je me souviens d'une technique d'un exo que j'avais traité il y a un an, je m'en suis inspiré, l'exercice ne parlait pas d'hyperplan. 

On a $\dim H=n-1$.
Soit $(e_1, \cdots, e_{n-1})$ une base de $H$. Soit $a \notin H$. Complétons cette famille en une base $(e_1, \cdots, e_{n-1},a)$ de $E$.

Considérons l'application : $ f : \mathcal L(E,\R) \longrightarrow \R^{n-1}$ tel que $f( u) =( f(e_1), \cdots, f(e_{n-1}))$.

• Puisque $u$ est une forme linéaire, alors $f$ est linéaire. 

• On a $\boxed{\ker (f)=D_H}$. En effet, une application s'annule sur $H$ si et seulement si $f(u)=(0, \cdots, 0)$ puisque $(e_1, \cdots, e_{n-1})$ est une base de $H$.
• On a $\boxed{Im (f)=\R^{n-1}}$. En effet, soit $(y_1, \cdots, y_{n-1}) \in \R^{n-1}$. Il existe une unique application linéaire $u$ de $E$ vers $\R$ tel que $\forall i \in [|1,n-1|] \ \ u(e_i)=y_i$ et $u(a)=0$. Ainsi $f(u)=(y_1, \cdots, y_{n-1})$. Donc $(y_1, \cdots, y_{n-1}) \in Im(f)$. 

Par suite, $D_H$ est bien un sous-espace vectoriel de $\mathcal L(E,\R)$, puisque c'est le noyau d'une application linéaire. D'après le théorème du rang on a :  $\dim \mathcal L(E,\R) = \dim ( \ker \ f) + \dim ( Im \ f)= \dim D_H + (n-1) \dim \R = \dim D_H +(n-1)$.

Donc $\boxed{ \dim D_H=1}$.

stfj

5. Soit $a\notin H. \forall x\in E, \exists (h,\lambda)\in H\times \mathbb R: x=h+\lambda a$. Soit alors $\varphi\in D_H^*\color{red}{(*)}$ . On a $\varphi(x)=\varphi(h+\lambda a)=\varphi(h)+\lambda \varphi(a)=\lambda \varphi(a)$ par hypothèse $\color{red}{(*)}$, $=\varphi(a)\phi(x)$ . Donc $\varphi\in \mathbb R \phi$ Et finalement $D_H^*$ est une droite vectoriel de $E^*$ engendrée par $\phi$. Donc $$\text{dim}D_H^*=1$$

OShine

@stfj merci pour ta solution alternative, ma solution à la question 5 est-elle trop compliquée ? 
Je me suis inspirée d'une technique que j'ai apprise dans mon livre de MPSI. 

stfj

désolé, je n'avais pas vu que tu avais proposé une solution à la question 5. De quel livre vient cet exercice ?

OShine

Ta solution est plus dans l'esprit du sujet.
C'est un sujet de ENS ULM pour lettres et sciences humaines.  Voici la suite et fin du problème.
6) Cette question me paraît triviale. Si $\ker (f-I)$ est un hyperplan, il est de dimension $n-1$ donc $Im(f-I)$ est de dimension $1$, c'est donc une droite vectorielle.
7) Montrons que $f_{\phi,u}$ est linéaire. Soient $a,b \in \R$ et $x,y \in E$. On a $f_{\phi,u} (ax+by)=ax+by+ \phi(ax+by)u$. Mais $\phi$ est linéaire donc $f_{\phi,u} ) =ax+by+a \phi(x)u +b \phi(y)u = af_{\phi,u} (x)+b f_{\phi,u} (y)$.$x \in f_{\phi,u} \iff f_{\phi,u} (x)-x=0 \iff \phi(x) u=0$. Je bloque ici.

stfj

7. $f(x)=x\iff \phi(x)=0\iff x\in \text{Ker}\,\phi  $ et on a prouvé précédemment que Ker$\phi$ est un hyperplan. Donc Ker$(f-I)$ est bien un hyperplan.
Soit $y\in \text{Im}(f-I), y=f(x)-x$ pour $x\in E$ . Alors $f(y)-y=f\circ f(x)-f(x)-(f(x)-x)=f(x+\phi(x)u)-2(x+\phi(x)u)+x=f(x)+\phi(x)f(u)-2x-2\phi(x)u+x=x+\phi(x)u+\phi(x)(u+\phi(u)u)-2x-2\phi(x)u+x=0$ car $\phi(u)=0$ par hypothèse.
Donc $f$ est une transvection de base Ker$\phi$ et de direction $\mathbb R u$.

OShine

Ok merci parfait, ce n'était pas difficile en effet !

OShine

Il y a une suite... J'essaie de faire ça dans la soirée.

stfj

Mais après cet exercice classique au moins pour ceux qui le posent, est-ce que tu vois ce qu'est une transvection ?(sur wikipedia, tu trouveras une illustration élémentaire avec une petite usine jaune déformée selon une transvection en une bleue)

NicoLeProf

Oui, je trouve ta solution trop compliquée OShine.

Voici ce que j'ai pour la question 5) : on montre rapidement que $D^*_H$ est un s.e.v de $E^*$ (le dual de $E$) en revenant à la définition . 
Soit $v \in E \setminus H$, $v \neq 0$. On note $\phi$ la forme linéaire de $E$ dans $\mathbb{R}$ telle que : $H=\ker \phi$ et $\phi(v)=1$ .

Soit maintenant $\psi \in D^*_H$ . Alors $H=\ker \psi=\ker \phi$ (car $H$ est inclus dans $\ker \psi$ et ces deux espaces vectoriels sont de dimension $n-1$) .

De plus, on note : $\psi(v)= \lambda$ . Alors d'après la question $3$, on a : $\psi=\lambda \phi$ donc la famille $(\phi)$ est une famille génératrice de $D^*_H$ . De plus, $\phi$ n'est pas la forme linéaire nulle de $E$ dans $\mathbb{R}$ donc la famille $(\phi)$ est libre.

Conclusion : $(\phi)$ est une base de $D^*_H$ et $\dim(D^*_H)=1$ .
En fait, pour cette preuve, je me suis inspiré de la dualité.

NicoLeProf

@OShine, si $x$ appartient à $\ker (f_{\phi,u}-I)$ alors : $\phi(x)u=0 \Rightarrow \phi(x)=0$ car $u \neq 0$ (je te rappelle que $\phi(x) \in \mathbb{R}$ car $\phi$ est une forme linéaire).

La suite est facile, je te laisse conclure !

De plus, ta rédaction est bizarre, tu t'es embrouillé je dirais. Et tu n'as pas besoin de démontrer la linéarité qui est supposée dans l'énoncé !

OShine

Ok mais je pense que la meilleure preuve est celle de @stfj et c'est la plus simple.

@stfj
Non concrètement je ne vois pas ce que c'est malgré wikipédia, je ne comprends pas grand chose à leur dessins.
C'est théorique et compliqué.

stfj

8. Par la définition donnée d'une transvection, $\ker(f-I)$ est un hyperplan $H$. D'après ce qu'on a vu, $\exists \phi \in E^*, \ \ker(f-I)=\ker\phi$.
9. $\phi(x-\phi(x)v)=...$

NicoLeProf

La suite est vraiment facile ! ^^'

Si seulement, il y avait cela à l'agreg lol

stfj

10. $f\neq I$ donc $\exists w\in E f(w)\neq w$. Soit $\lambda=\phi(w)$ et $v=\lambda^{-1}w$. On a $\phi(v)=1$ et $u=v-f(v)\neq 0$. On a alors pour $x\in E, x=h+\xi v$: $$f(x)=f(h)+\xi f(v), f(x)-x=f(h)+\xi f(v)-h-\xi v=f(h)-h+\xi u=0+\phi(x) u$$par définition de $\phi$ et de $H$. Donc $f(x)=x+\phi(x) u=f_{\phi,u}(x).$ Donc $f=f_{\phi,u}.$ QED.

stfj

Je suis wikipédien et c'est moi qui ai fait l'illustration avec la petite "usine" bleue/jaune qui illustre l'article wp "transvection" :  ce n'est pas compliqué : $E=\mathbb R^2, x=(\xi, \eta), \phi(x)=\eta, u=(1,0), f(x)=(\xi,\eta)+\eta(1,0)=(\xi, \eta)+(\eta,0)=(\xi+\eta,\eta)$. Ceci est expliqué dans l'exemple de l'article à côté de l'illustration avec la base et la direction de la transvection.

OShine

Bon tu as tout résolu je passerai à un autre sujet.

C'est d'un niveau très élevé pour les élèves de lettres...
C'est facile pour les élèves de scientifique.

stfj

C'est des questions de cours sur les transvections. Et tout le travail est mâché dans l'exercice. J'ai résolu pour t'inviter à réfléchir à des exemples simples de transvections comme celle proposée dans l'article wp, quitte à revenir à cet exercice plus tard : ça n'a aucun sens ce type d'exo si on n'a aucune idée de ce qu'est une transvection. 

NicoLeProf

On peut montrer pour aller plus loin que :

• dans une certaine base bien choisie de $E$, la matrice d'une transvection est de la forme : $I_n+\lambda E_{i,j}$ avec $i \neq j$ (ou bien $I_n$) où $I_n$ est la matrice identité de $M_n(\mathbb{K})$ et $E_{i,j}$ désigne une matrice élémentaire dont le coefficient $(i,j)$ vaut $1$ et les autres valent $0$ .
  
• Le groupe spécial linéaire $SL_n(\mathbb{K})$ (ensemble des matrices carrées d'ordre $n$ et de déterminant $1$) est engendré par les transvections.
  
• Pour $A \in M_n(\mathbb{K})$ et $T_{i,j}(\lambda)=I_n+\lambda E_{i,j}$, montrer que la matrice $T_{i,j}(\lambda)A$ est obtenue à partir de $A$ en effectuant l'opération élémentaire : $L_i \leftarrow L_i+ \lambda L_j$ .
  

Ce sont toutes des preuves de cours mais il faut savoir les faire pour l'agrégation (écrits ou oraux)... Je vais peut-être m'y coller d'ailleurs sans regarder le cours évidemment. 

NicoLeProf

Je commence par prouver le point 1) . On a démontré suite à l'exercice d'OShine que comme $f$ est une transvection de $E$ dans $E$ alors il existe une forme linéaire $\phi \in E^*$ non nulle (si $\phi$ est nulle alors $f=id_E$) telle que $\ker \phi=\ker (f-id_E)$ et un vecteur $u$ de $\ker(f-id_E)$ non nul tels que : $f(x)=x+\phi(x)u$ .

D'après la définition de $f$, $\ker(f-id_E)$ est un hyperplan. Notons $(e_1,...,e_{n-2},u)$ une base de $\ker(f-id_E)$ .

On complète cette famille en une base de $E$ en ajoutant un vecteur $v \neq 0$ et tel que $ v \notin \ker(f-id_E)$.

Donc la famille $B=(e_1,...,e_{n-2},u,v)$ est une base de $E$.

Pour tout $1 \leq i \leq n-2$, $f(e_i)=e_i$ car $e_i \in \ker (f-id_E)$ . De plus, $f(u)=u$ .

De plus, $f(v)=v+ \phi(v)u=v+\lambda u$ en notant $\phi(v)=\lambda$ .

La matrice de $f$ notée $T_{i,j}(\lambda)$ dans cette base est donc de la forme $I_n+\lambda E_{i,j}$ avec $i \neq j$ d'ailleurs (ici $I_n+\lambda E_{n-1,n}$ où $E_{i,j}$ est la matrice élémentaire définie précédemment. En fonction de l'ordre des vecteurs de la base $B$.

stfj

@NicoLeProf : dans le cas $n=2$, on choisit $u$ une base de $H=\ker(f-id_E)$ et $v\notin H$. On a  la base $B=(u,v)$ de $E$. On a $f(u)=u$. De plus, $f(v)=v+\lambda u$ comme tu l'as noté. Par exemple, si $\lambda=2$, on retrouve l'$\color{red}\text{exemple}$ cité plus haut (article de wp). $Mat(f)=\begin{bmatrix}1 & 2 \\0 & 1\end{bmatrix}$. On a $$\begin{bmatrix}1 & 2 \\0 & 1\end{bmatrix}\times \begin{bmatrix}a &  b\\c & d\end{bmatrix} =\begin{bmatrix}a +2c&  b+2d\\c & d\end{bmatrix}$$

NicoLeProf

Le point 2) me fait un peu de résistance, je dois y réfléchir davantage...

Je passe donc directement au point 3) plus abordable : on note $A=(a_{k,\ell}) \in M_n(\mathbb{K})$ . On veut calculer $T_{i,j}(\lambda)A=A+\lambda E_{i,j}A$ .

On commence par calculer $E_{i,j}A$ .

On a pour tous $k, \ell \in \{1,...,n\}$, $[E_{i,j}A]_{k,\ell}=\displaystyle \sum\limits_{p=1}^n [E_{i,j}]_{k,p} a_{p,\ell}=\displaystyle \sum\limits_{p=1}^n \delta_{ik} \delta_{jp} a_{p,\ell}=\delta_{ik} a_{j,\ell}= \begin{cases} a_{j,\ell} \text{ si $i=k$}  \\ 0 \text{ sinon} \end{cases}$ .

Ainsi, la matrice $E_{i,j}A$ est la matrice dont la $i$ème ligne est la $j$ème ligne de $A$ et dont tous les autres coefficients sont nuls.

Par conséquent, la matrice $A+\lambda E_{i,j}A$ est la matrice dont la $i$ème ligne est $L_i+\lambda L_j$ (où $L_i$ est la $i$ème ligne de $A$ et $L_j$ est la $j$ème ligne de $A$) et dont tous les autres coefficients sont ceux de la matrice $A$ .

Conclusion : $T_{i,j}(\lambda)A$ est bien la matrice obtenue à partir de $A$ en effectuant l'opération élémentaire : $L_i \leftarrow L_i+\lambda L_j$ .

stfj

A l'agrégation de mathématiques, un exemple vaudra toujours mieux que de longs calculs fastidieux, à moins que la technique des longs calculs avec la "science des indices" soit l'objet d'une question. C'est un concours d'enseignants, il s'agit de montrer qu'on est capable de simplifier la tâche pour ses futurs élèves, n'est-ce pas ? Dans les programmes de collège et lycée, on trouve fréquemment : "l'excès de technicité est à éviter."
Tu as oublié $$\begin{bmatrix}a &  b\\c & d\end{bmatrix}\times\begin{bmatrix}1 & 2 \\0 & 1\end{bmatrix}=...$$

OShine

Ok je vais essayer de comprendre ce qu'est une transvection.
Je vais relire l'article.
Je connais les matrices de transvection mais c'est tout.

NicoLeProf

stfj a dit :

https://les-mathematiques.net/vanilla/index.php?p=/discussion/2333056/hyperplan#latest

Cela donne : $\begin{bmatrix}a &  2a+b \\c & 2c+d\end{bmatrix}$ .

La première colonne de cette matrice est la première colonne de $A$.

C'est un appel du pied pour démontrer l'autre opération élémentaire, sur les colonnes cette fois !!! Je m'y colle !

Edit : correction d'une étourderie sur le produit matriciel ^^'

stfj

C'est un conseil -qui vaut ce qu'il vaut- de NE PAS démontrer l'autre opération élémentaire : une fois suffit largement; ensuite, on se contente d'exemples comme celui de $\begin{bmatrix}a &  b+2a\\c & d+2c\end{bmatrix}$

NicoLeProf

Point bonus qui ressemble fortement au point 3) mais cela ne me fait pas de mal de pratiquer le calcul matriciel à $1$ semaine et demie de l'agreg !  On note $A=(a_{k,\ell}) \in M_n(\mathbb{K})$ . On veut calculer $AT_{i,j}(\lambda)=A+\lambda AE_{i,j}$ .

On commence par calculer $AE_{i,j}$ .

On a pour tous $k, \ell \in \{1,...,n\}$, $[AE_{i,j}]_{k,\ell}=\displaystyle \sum\limits_{p=1}^n a_{k,p} [E_{i,j}]_{p,\ell} =\displaystyle \sum\limits_{p=1}^n a_{k,p} \delta_{ip} \delta_{j \ell} =\delta_{j \ell} a_{k,i}= \begin{cases} a_{k,i} \text{ si $j=\ell$}  \\ 0 \text{ sinon} \end{cases}$ .

Ainsi, la matrice $AE_{i,j}$ est la matrice dont la $j$ème colonne est la $i$ème colonne de $A$ et dont tous les autres coefficients sont nuls.

Par conséquent, la matrice $A+\lambda AE_{i,j}$ est la matrice dont la $j$ème colonne est $C_j+\lambda C_i$ (où $C_i$ est la $i$ème colonne de $A$ et $C_j$ est la $j$ème colonne de $A$) et dont tous les autres coefficients sont ceux de la matrice $A$ .

Conclusion : $ AT_{i,j}(\lambda)$ est bien la matrice obtenue à partir de $A$ en effectuant l'opération élémentaire : $C_j \leftarrow C_j+\lambda C_i$ .

NicoLeProf

Ah zut trop tard haha ^^'

Je suis d'accord avec toi stfj mais il faut savoir refaire ce genre de démonstrations pour le concours (et puis, ce n'est pas très long ni très difficile). Cela peut être redemandé à l'écrit comme à l'oral.

Après, si la question ne demande pas de démonstration théorique, un exemple au brouillon suffit pour gagner du temps, je suis complètement d'accord !!! ^^'

Amédé

Question de jury: $\theta\in \R$. Ecrire $\begin{pmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta)\end{pmatrix}$ comme produite de transvections

OShine

Question difficile @Amédé

OShine

@stfj
Je comprends ce qu'est une matrice de transvection. 
Je ne comprends rien à l'exemple de wikipédia avec ton dessin. C'est quoi ces couleurs ? C'est quoi ces formes géométriques étranges ? 
La rédaction est trop succincte pour espérer comprendre quoi que ce soit, peut-être que cet exemple est à détailler plus pour que les nuls comme moi puissent comprendre quelque chose.
C'est quoi le "on retrouve la forme condition équivalente n°2" ? Ce n'est pas très clair.
Il y a un passage en latex difficilement lisible à corriger.

stfj

@OShine : bonjour . Le but est d'illustrer la notion de transvection pour le plus grand nombre. (wikipedia est une encyclopédie qui s'adresse au plus grand nombre). On choisit une application simple de $\mathbb R^2$ dans $\mathbb R^2$ qu'on peut d'ailleurs restreindre à une application de $\mathbb Z^2 $ dans $\mathbb Z^2$(bref ne travailler qu'avec les nœuds du quadrillage)

C'est l'application $$t:(x,y)\mapsto (x+2y,y)$$ pour laquelle on affirme que c'est une transvection. On considère alors un polygone jaune (que j'appelle "une petite usine" à cause des "toits"), notons-le $U$. On peut même définir $U$ formellement par $$U:=\{(2,0),...,(3,1),..., (4,0)\}$$ et on cherche l'image de $U$ par $t$, que je note $t(U)$ comme d'habitude. Par exemple sur le dessin ci-dessus, on a cherché $t((3,2))$ et obtenu $(3+2\times2,2)=(7,2)$ que tu peux repérer sur l'image. Bref l'image de la petite usine jaune, $t(U)$,  est la petite usine bleue. Pour le lecteur occasionnel de wp, il aura au moins vu l'effet d'une transvection clairement définie mathématiquement sur une figure du plan. As-tu compris ?