Enseigner la géométrie en 2023 : quelle place pour l'algèbre linéaire ?

Dom

🤣
« Il est évident que la pente change ». 

Je t’incite à essayer, même avec des lycéens (je l’ai déjà vu en terminale…). Bien entendu, certains auront déjà rencontré cela, mais pour les autres, tu me diras…
Et ne les engueule pas si leurs « ça se voit » n’est pas celui que tu souhaites. Tu vas en voir un bon tiers tracer la diagonale dans le deuxième rectangle. Un bon tiers…

Je t’écoute attentivement. Tu restes bloquée de ton côté. J’argumente et tu t’enfermes sans argument (sauf « ça se voit »… hélas les maths… ce n’est pas ça…). 

Je répète que je me fous des personnalités, car ici, je ne connais personne. Je ne peux que me fier à leurs discours. Comment faire autrement ?

Foys

stfj a dit :

 Or, il y a un lien direct des espaces vectoriels ou affines vers la topologie(il suffit de rajouter une structure). Et cela ne pose donc aucun problème. J'ignore si ce lien existe avec la géométrie d'Euclide/Hilbert.

Le plan et l'espace de la géométrie d'Hilbert/Euclide sont des espaces métriques.

Vassillia

Je veux bien te croire que ce n'est pas évident pour eux et qu'ils vont se tromper mais justement c'est parceque leurs profs précédents ne les ont pas habitués à réfléchir ainsi.
Si tu me dis qu'un lycéen n'est pas capable de comprendre mon argument sur la pente, je ne te crois pas, désolée et j'enseigne aussi à des lycéens (certes privilégiés) donc je vois plus ou moins de quoi ils sont capables.
C'est pourtant simple, on trouve ce qu'on aimerait bien démontrer par du "ça se voit" puis on démontre par du calcul (ici du simple comptage) si ça c'est pas des maths, c'est bien imité. Et si la démonstration montre qu'on s'est trompé avec le "ça se voit" c'est pas grave, c'est pour ça qu'il faut toujours démontrer.

stfj

@Foys : ok. Qu'est-ce qu'un nombre en géométrie d'Hilbert/Euclide? Qu'est-ce que $0$? Qu'est-ce que $1$? Qu'est-ce qu'un nombre ?$\mathbb R $ est-il supposé déjà construit? Soit $A$ et $B$ deux points. Comment définit-on $d(A,B)$? L'inégalité triangulaire, c'est un axiome? cela se démontre ? 

Foys

@stfj

Il faut regarder dans les axiomatiques proposées pour la géométrie du XXième siècle (Hilbert/Tarski/Birkhoff etc).

De toute façon soit $E$ un ensemble. Soit $M$ un ensemble ordonné ayant un plus petit élément $z$ et dans lequel toute partie finie est minorée. Soit $f: E^2\to M$ une fonction. Soit $\tau$ l'ensemble des parties $V$ de $E$ telles que pour tout $x\in V$, il existe $r\in M$ tel que $r>z$ et tel que pour tout $y\in E$, si $f(x,y)<r$ alors $y\in V$. Alors $\tau$ est une topologie sur $E$. Rien n'empêche d'ajouter ultérieurement des exigences sur $M$ et $f$ pour avoir des propriétés plus riches sur $\tau$ (séparation, caractérisations séquentielles etc).

Dom

Je ne tiens pas compte de ta diatribe sur la faute des profs précédents. Et que ce soit vrai ou faux d’ailleurs. La discussion n’est pas « voilà comment on aurait pu être dans une autre situation ? » mais « en 2023, en l’état, que faire ? ». Mais j’ai tellement vu des profs de L1 dire « que font les profs de lycée » et idem « que font les profs de collège » et idem « que font les profs des écoles »… que ce genre de propos, je les trouve « faciles ». En fait je le pense parfois d’une manière systémique mais je ne donne pas de leçons là-dessus non plus. Soyons profs des écoles et voyons le carnage…

Les lycéens : comme quoi, l’échange est utile, ce n’est pas ce que j’ai dit. Si tu leur parles de pente, oui (qui a dit le contraire ?). Mais leur parler de pente c’est leur donner la clé. Sans ça, une grande majorité (et je ne m’en moque pas ! je dis que c’est naturel) va faire la figure en ne voyant pas que la pente change et en traçant grossièrement cette maudite diagonale. 

Alors si le prof donne la clé, il ne faut pas parler de les faire réfléchir.

Pour la partie « calcul », je précise qu’on était au collège (4e) ou ces rudiments de distributivité double ne sont pas des rudiments. Tu sembles omettre cet argument. Tu l’effaces. Il ne te convient pas. 

stfj

Je joins ici ma construction "à la règle trop courte": la sécante $d_1$ coupant respectivement $\color{blue}f$ et $\color{blue}g$ en $I$ et $J$ est choisie de façon arbitraire. Au lieu de $k$, j'aurais dû mettre $d_{3bis}$ . Je rappelle ici le lien vers le problème initial pour ceux qui ne le connaîtraient pas.

pldx1

Bonjour.

Comment enseigner ? Intéressante question. Mais il serait surprenant d'obtenir une réponse pertinente sans commencer par se demander comment enseigner quoi ?

Si l'on veut bien considérer que faire des mathématiques c'est (1) trouver des résultats (2) trouver des preuves (3) vérifier que les preuves prouvent effectivement les résultats, il faut donc enseigner à trouver/trouver/vérifier. 

Prenons pour exemple l'exercice "montrer que le point qui voit le triangle des in-contacts orthogonalement au triangle des ex-contacts est le point de Prasolov du triangle des in-contacts" peut se faire de deux façons. 

méthode (A). On commence par calculer (ency@mkortho)(matcev(vX(7)), matcev(vX(8))) qui donne 1071. Puis on montre que X(DEF,68) n'est autre que X(ABC,1071). 

méthode (B).  On fait une figure sous geogebra. On trace les perpendiculaires qui vont bien et on détermine le voyeur orthogonal. On constate qu'il coïncide avec le DEF-point de Prasolov. Puis on agite les points $A,B,C$ et on constate que la propriété continue de se vérifier.  

Quand on a utilisé l'une de ces deux méthodes, on a établi au delà de tout doute possible que jamais personne ne trouvera de contre-exemple à la propriété annoncée (on suppose que le triangle est triangulaire i.e. non aplati). N'est-ce pas là la définition d'une preuve ? Il se trouve que (A) rend évident le fait que la propriété a été prouvée, sans pour autant rendre la propriété "intuitive". Tandis que (B) rend évidente la propriété annoncée, sans pour autant qu'il soit intuitif que l'agitation a créé un ensemble "suffisamment trop vaste"  pour qu'un certain polynôme formel puisse éviter d'être identiquement nul. 

On a une sorte de "principe d'Heisenberg": "manque d'intuitivité" $\times$ "manque de provativité" $>0$. Et donc, il faut marcher sur ses deux jambes au lieu de vouloir être "tout formel" ou bien "tout intuitif".  

A part cela, il reste à appliquer correctement les "Instructions" issues par l'Administration Centrale: "tout excès de technicité est à proscrire" cela ne veut pas dire: "moins t'es technique, mieux ce sera". Cela veut dire au contraire: "la technicité est à développer" et il faut utiliser un contexte où cette technicité est pertinente et non excessive. Les calculs en coordonnées sont excellents pour cela.  

Cordialement, Pierre.

stfj

Les mathématiciennes et mathématiciens ont mis collectivement des millénaires à découvrir les vecteurs(classes d'équipollence de bipoints si l'on veut tenter une adéquation avec l'épistémologie). Dans le plan affine, on obtient un espace vectoriel euclidien de dimension deux; dans l'espace, de dimension trois. Et l'on a voulu faire croire que d'innocents collégiens allaient trouver tellement naturel l'introduction de ces objets qui ont nécessité des milliers d'années de recherche pour être découverts, qu'ils allaient former des générations d'êtres libres, pensants, armés de logique,... les "winners" des années 1980. Quelle bêtise ! Quel gâchis dénoncé très tôt par des Dieudonné ou encore Godement, à qui on ne la faisait pas. 

Or, il est une vérité mathématique toute bête, connue de tous : un plan vectoriel réel est isomorphe à $\mathbb R^2$, un espace à $\mathbb R^3$, les objets mathématiques les plus élémentaires qui soient, étudiés dès la 6è/5è au moins en restreignant l'étude à $\mathbb Z^2$. Des pédagogues reconnus internationalement tels que Serge Lang ont eu beau le montrer dans leurs livres les plus élémentaires, les a-t-on écoutés ou seulement lus? Que nenni ! Il fallait qu'on écoutasse des propositions bien de chez nous, celle de Choquet, celles de Queysanne, de Revuz... Complètement à côté de la plaque, limite délirantes. L'a-t-on reconnu ? Toujours pas je crois. Evidemment que les calculs en coordonnés sont excellents pour développer la technicité.

Pour conclure, voici [pour rappel] le dernier paragraphe de la préface célèbre d'Algèbre linéaire et géométrie élémentaire de Jean Dieudonné  

"J'espère qu'on me croira sans peine si j'ajoute, pour terminer; que je n'ai aucun intérêt personnel dans ces questions d'Enseignement secondaire, et qu'il me chaut fort peu de savoir si, où et quand il y aura une réforme de cet enseignement, ni ce qu'en seront les modalités. J'ai simplement voulu verser au dossier de l'historien futur un exemple de ce que l'on pourrait faire en la matière si l'on cherchait à agir de façon rationnelle."

Il y en a qui ont de la chance.

Dom

« Des pédagogues reconnus internationalement »
Personne ne fait autorité en pédagogie (ou plutôt… si… hélas… des choix ont été faits… voir Meirieu). Inutile d’user d’arguments de la sorte. J’oserais même dire que si c’est une « reconnaissance internationale » alors je m’en méfie expressément. 

Ceci pour ponctuer un peu ton monologue depuis deux jours. 

Vassillia

Tout l'enjeu est donc de leur faire voir ce que sont des classes d'équipollence de bipoints (le déplacement entre les points) et de leur faire calculer par soustraction des coordonnées sans les emberlificoter avec des définitions formelles à n'en plus finir.
C'est pas facile mais ça devrait être jouable, n'est-ce pas pour cela qu'on fait ce métier ?

@Dom Tu es têtu quand même, je ne leur donne pas la clé de ce problème, je leur donne la clé de tous les problèmes car je veux qu'ils voient une droite par sa pente donc bien sûr qu'il n'y a pas à réfléchir à ce sujet. Tu noteras que j'étais d'accord avec toi pour faire du découpage pour ceux qui ont du mal avec le calcul littéral et tu te doutes bien que je n'hésiterai pas à faire du hors programme si je pense que c'est utile et compréhensible par mes élèves.

Dom

Je n’avais pas bien compris l’échange alors… ce n’est pas grave. 

Quant à donner la clé, là encore, je suis sûr que tous les profs la donnent. La question est plutôt « quand la donner ? ». J’ai cru que tu la donnais hâtivement.

Bon, cette fois-ci, il faut faire une « pause fil ». 

stfj

@Dom : j'ai cité @pldx1 :"A part cela, il reste à appliquer correctement les "Instructions" issues par l'Administration Centrale: "tout excès de technicité est à proscrire" cela ne veut pas dire: "moins t'es technique, mieux ce sera". Cela veut dire au contraire: "la technicité est à développer" et il faut utiliser un contexte où cette technicité est pertinente et non excessive. Les calculs en coordonnées sont excellents pour cela.  " J'ai tiré mes conclusions de la réponse que @Foys a apporté gentiment à mes questions  : "Il faut regarder dans les axiomatiques proposées pour la géométrie du XXième siècle (Hilbert/Tarski/Birkhoff etc)." [au passage , Birkhoff , c'est le même que Birkhoff & MacLane?] La démo que tu as fournie pour le théorème de Pythagore est celle que j'utilise depuis 25 ans tellement elle me plaît. J'ai réfléchi à une réponse de @Alain24sur les géométries non-euclidiennes... Je vais me pencher sur deux exercices que @dp m'a proposé. Tes échanges avec @Vassillia m'intéressent... Et je suis dieudonniste et godementiste car cela m'évite de réfléchir.

stfj

Birkhoff est le père de Birkhoff.

biguine_equation

Montrer que le point qui voit le triangle des in-contacts orthogonalement au triangle des ex-contacts est le point de Prasolov du triangle des in-contacts … On commence par calculer $\textbf{ency@mkortho(matcev)(vx(7)), (matcev)(vX(8)))}$ 

Limpide ! Si avec ça, les enseignants et leurs élèves ne trouvent pas la voie royale…

Ce genre de posts est une insulte, une de plus, à tous les naufragés de la science mathématique. 

Foys

@stfj le coauteur du livre d'algèbre auquel tu penses est Garrett Birkhoff; c'est son père George qui a introduit l'axiomatique de la géométrie dont je parlais.

https://en.wikipedia.org/wiki/George_David_Birkhoff

https://en.wikipedia.org/wiki/Garrett_Birkhoff

stfj

@Foys : merci

stfj

Intéressant  le travail de Birkhoff père. Ce court extrait me donne envie d'en connaître davantage.

stfj

@pldx1 : si j'ai bien compris ce que j'ai retenu de la lecture de Algèbre linéaire et géométrie élémentaire de Dieudonné ou encore du début élémentaire de Linear algebra I de Serge Lang (où il écrit par exemple qu'il est opposé à prendre la relation $$A.B:=\|A\|.\|B\|\cos \theta$$comme définition du produit scalaire-ce qui relève bien en 2023 d'un choix à faire dans l'enseignement secondaire français-), il s'agit bien plus que de quelques "calculs en coordonnées". Il s'agirait, si j'ai bien compris, de mettre en place de façon on ne peut plus consciente chez les enseignants du secondaire dès la classe de seconde la volonté de mettre en évidence la structure d'espace vectoriel euclidien de $(\mathbb R^2,+,.,<.,.>)$, autrement dit $$\forall a,b,c,d \in \mathbb R, (a,\color{red}b\color{black})+(c,\color{red}d\color{black}):=(a+c,\color{red}b+d\color{black})$$ $$\forall \lambda\in \mathbb R, \lambda(a,b):=...$$ $$(a,\color{red}b\color{black}).(c,\color{red}d\color{black})\text{ défini comme le nombre }(ac+\color{red}bd\color{black})$$ après avoir fait travaillé les élèves de collège dans des repères, où, à travers des exemples multiples et variés comme je me suis efforcé de le montrer tout le long de ce fil, ces définitions ne leur paraîtraient pas hors sol.
Pour ma part, je ne connais rien* de plus simple, intuitif, naturel, susceptible de généralisations intéressantes, facile à utiliser... en maths que l'objet mathématique $\mathbb R^2$.
_________________________
* Comme tous les matheux de la planète. Désolé d'enfoncer des portes ouvertes.

Vassillia

@biguine_equation

Euh ben oui, c'est à peu près clair, je ne refais pas la figure car elle est dans ce fil https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2406333
On se place dans le triangle ABC
X(7) est le point de Gergonne, c'est à dire l'intersection des droites passant par un sommet et les points de contact du cercle inscrit.
X(8) est le point de Nagel, c'est à dire l'intersection des droites passant par un sommet et les points de contact des cercles exinscrits
Bon évidemment, je ne le savais pas mais je sais me servir de google alors que peut t'il bien fabriquer avec sa formule ?

Et bien, à mon humble avis matcev sert à calculer les céviennes (les droites dont je parlais il y a un instant pour trouver les points de contact)
Ensuite, il utilise mkortho pour calculer le point X puisque cela correspond à l'intersection des droites projetant orthogonalement les points trouvés précédemment sur les droites trouvées précédemment.
Est-ce que je peux taper sa formule ? Non, je n'ai pas codé de macro codant son bazar
Est-ce que je peux faire la même chose ? Oui, je sais me servir d'un logiciel de calcul formel

Ensuite, Je vais au numéro 1071 de https://faculty.evansville.edu/ck6/encyclopedia/ETCPart2.html et j'apprends X(1071) = X(68)-of-intouch triangle
Bon admettons alors je vais au numéro 68 et j'apprends X(68) est le Prasolov Point

Voilà, voilà, et je suis de la génération qui officiellement est nulle en géométrie mais aussi celle qui sait utiliser les outils modernes. J'ai le bon gout de ne pas trouver insultant tout ce que je ne sais pas faire mais d'upgrader mes compétences lorsque je juge cela utile. Attention, je ne dis pas non plus qu'il faut enseigner cela au collège ou au lycée, entendons nous bien.

stfj

@Vassillia : des générations d'enseignants de mathématiques ont essayé de transmettre , dit de façon plus ou moins explicite, qu'un vecteur $\vec{AB}$ est la classe d'équipollence du bipoint $(A,B)$: ils n'y sont pas parvenu, il faut l'admettre. Donc on en tire les leçons, on n'essaie plus. De toute façon, dès 1964, Dieudonné avait mis en garde en disant qu'il était farouchement opposé à ce qu'il appelait l' "échafaudage auxiliaire". Cela enlève un poids, non? Ce qu'on peut faire raisonnablement, comme l'enseignaient François Liret et Dominique Martinais par exemple à Paris VII, c'est...

$$\text{travailler dans }\mathbb R^2, \mathbb R^3$$
bref en substance ce qu'écrivait Dieudonné, Lang(héritier d' Artin) ou sous-entendait Dixmier entre autres... Bref tu enlèves tout ce qui ne sert à rien et a gêné des générations d'élèves dans leur apprentissage des mathématiques(d'où -entre autres problèmes comme les classes surchargées- le niveau actuel), et tu ne gardes que ce qui leur servira plus tard, la structure essentielle d'espace vectoriel réel en dimension deux ou trois. Comme il n'y a pas grand chose de plus simple en maths, cela ne devrait pas être un défi trop grand à atteindre : en tout cas, mes 6è et 5è d'un collège lambda parisien y arrivent sans trop de mal au bout d'un trimestre et ont déjà vu, comme je l'ai montré dans ce fil, une transvection, des homothéties, des similitudes directes, des similitudes indirectes non triviales, une projection centrale qui ne conserve pas les milieux, angles inscrits et au centre, ellipse, hexagramme mystique de Pascal... En tout cas, c'est ce que je fais depuis 25 ans et les inspecteurs n'y ont rien vu à redire vu que c'est des matheux. Quand le niveau est si bas, entre la pesanteur et la grâce, mieux vaut choisir la pesanteur : c'est moche, calculatoire, désincarné, relevant davantage de la technique que d'une science aux prétentions célestes, mais c'est terriblement efficace. N'est-ce pas ?

stfj

Pour illustrer mon propos, je me propose de refaire la démonstration classique de la relation entre angle inscrit dans un cercle et angle au centre : 
Avec les notations de la figure, je vais montrer que $(\vec{AM},\vec{AJ})=2(\vec{FM},\vec{FJ})\color{red}(*)$:

$MAF$ est isocèle donc $(\vec{MF},\vec{MA})=(\vec{FA},\vec{FM})$. Or la somme des angles est $\varpi$ dans $MAF$ donc $$(\vec{AM},\vec{AF})=\varpi-2(\vec{FA},\vec{FM})$$En travaillant de même dans $JAF$, on obtient finalement $\color{red}(*)$.
___________________________
En classe de seconde, j'aurais adoré vérifier sur la figure proposée que pour $A=0, J=(-3,-4), M=(4,-3)$, on a $M.J=0$ et que $\cos(J-B,M-B)=\frac{\sqrt2}{2}$

JLapin

Tu veux qu'on te dise qu'on est évidemment d'accord avec toi mais désolé, je préfère une démonstration à l'ancienne du fait que les médiatrices ou les hauteurs sont concourantes  et l'apprentissage rugueux mais indispensable de la démonstration par le schéma "hypothèse - conclusion - démonstration" en s'appuyant sur les propriétés du cours sur les triangles, les parallélogrammes, etc. à une exposition d'hexagrammes fussent-ils très jolis.

Pour contrebalancer mes propos, félicitations pour l'investissement que tu montres !

stfj

@JLapin : j'ai énormément de mal à me faire comprendre. Je considère comme toi qu'au collège et même au lycée, à côté de l'apprentissage du calcul vectoriel, il est préférable pour l'élève de proposer une démonstration à l'ancienne du fait que les médiatrices ou les hauteurs sont concourantes  et l'apprentissage rugueux mais indispensable de la démonstration par le schéma "hypothèse - conclusion - démonstration" en s'appuyant sur les propriétés du cours sur les triangles, les parallélogrammes, etc.

 Mon propos se limite à l'abandon des espaces affines au lycée pour remplacer  cela par du travail facile dans $$\mathbb R^2, \mathbb R^3$$où sont définis les droites affines $a+D$ et les plans affines $b+P$, avec $a,b\in E$ et $D,P$ droite vectorielle et plan vectoriel.

JLapin

Facile de montrer que les trois hauteurs d'un triangle quelconque de $\R^2$ sont concourantes ? Je demande à voir.

stfj

@JLapin : tu ne m'as pas bien lu. Je suis pour une démonstration à l'ancienne du fait que les trois hauteurs sont concourantes. Je suis sûr que nous sommes en réalité exactement sur la même longueur d'onde.

stfj

Il suffit de jeter un coup d'oeil à la démonstration classique que j'ai proposée de la relation entre angle inscrit dans un cercle et angle au centre.

stfj

Je n'ai pas la prétention avec mes petits bras de renouveler l'enseignement de la géométrie en France, cela serait ridicule et @AD aurait eu la bonté de fermer la discussion j'espère. Je veux juste témoigner de 25 ans de pratique où dès le début j'ai été fortement influencé par les idées de Jean Dieudonné que j'avais cru comprendre à travers la préface d'Algèbre linéaire et géométrie élémentaire. Dans ce livre du prof célèbre, uniquement des espaces vectoriels réels essentiellement de dimension deux et trois , pas une seule fois la notation $$\vec{AB}$$à peine insiste -t-il sur le sens à donner à $$b-a$$charge au lecteur de le faire pour suivre les démonstrations nombreuses, des thèmes d'exercices bourrés de géométrie élémentaire, plein d'idées originales pour permettre à un jeune prof d'agrémenter son cours.

On ouvre maintenant un manuel de lycée : des segments fléchés partout, la "relation de Chasles" répétée jusqu'à la nausée, la structure vectorielle nulle part mise en évidence. Une mère n'y reconnaîtrait pas ses petits. Question qui me taraude depuis 25 ans : qu'est-ce que c'est que ce bins?

pldx1

Bonjour,

biguine_equation a dit :

Montrer que le point qui voit le triangle des in-contacts orthogonalement au triangle des ex-contacts est le point de Prasolov du triangle des in-contacts … On commence par calculer $\textbf{ency@mkortho(matcev)(vx(7)), (matcev)(vX(8)))}$ 

Limpide ! Si avec ça, les enseignants et leurs élèves ne trouvent pas la voie royale…

Ce genre de posts est une insulte, une de plus, à tous les naufragés de la science mathématique. 

biguine_equation se décrit comme un naufragé de la science mathématique. Mais cela ressemble à un  embellissement de la réalité. En fait, biguine_equation semble d'abord être un naufragé de cette prétendue "lecture globale" où l'on se limite à imaginer ce qui pourrait bien figurer entre quelques bribes péniblement déchiffrées.

J'ai présenté  une "méthode (A)" comme un calcul formel, produisant une preuve irréfutable quoique très peu intuitive. J'ai ensuite présenté une "méthode (B)", plus intuitive quant au résultat, mais dont la valeur provatoire est largement moins intuitive.

Et alors biguine_equation vient se plaindre de son incapacité à intuiter la "méthode (A)". C'est ce qui fait la différence entre un naufragé et un apprenant en science mathématique. Si la méthode (B) demande de tracer la droite $AD$, et que le naufragé trace la droite $CD$, il n'aura aucun  droit à se plaindre et à prétendre qu'il est insulté. Si tu te goures, c'est toi qui t'es gouré et personne d'autre.

Si la méthode (A) propose d'utiliser   $\textbf{(ency@mkortho)(matcev(vX(7)), matcev(vX(8)) )}$ et que le naufragé utilise  $\textbf{ency@mkortho(matcev)(vx(7)), (matcev)(vX(8)))}$ à la place, c'est le naufragé de la lecture/écriture qui s'est gouré, et personne d'autre. 

Avant d'espérer intuiter un texte formel, il faut commencer par savoir le recopier sans erreur.

Cordialement, Pierre.

pldx1

Les trois hauteurs d'un triangle sont concourantes. En effet, on trace par chaque sommet la parallèle au côté opposé. Puis on
trace les médiatrices du trigone ainsi obtenu. Et voilà, c'est déjà fini.

stfj

Je recopie une démonstration proposée par Daniel Perrin du fait que les trois hauteurs d'un triangle $ABC$ du plan $\mathcal P$ sont concourantes (p.27):
$\forall O \in\mathcal P, ( \vec{OB} − \vec{OC}| \vec{OA}) + (\vec{OC} − \vec{OA}| \vec{OB}) + (\vec{OA} − \vec{OB}| \vec{OC}) = 0$.
En particulier, si $O$ désigne le point d'intersection de deux hauteurs, cette égalité prouve que $O$ appartient aussi à la troisième hauteur.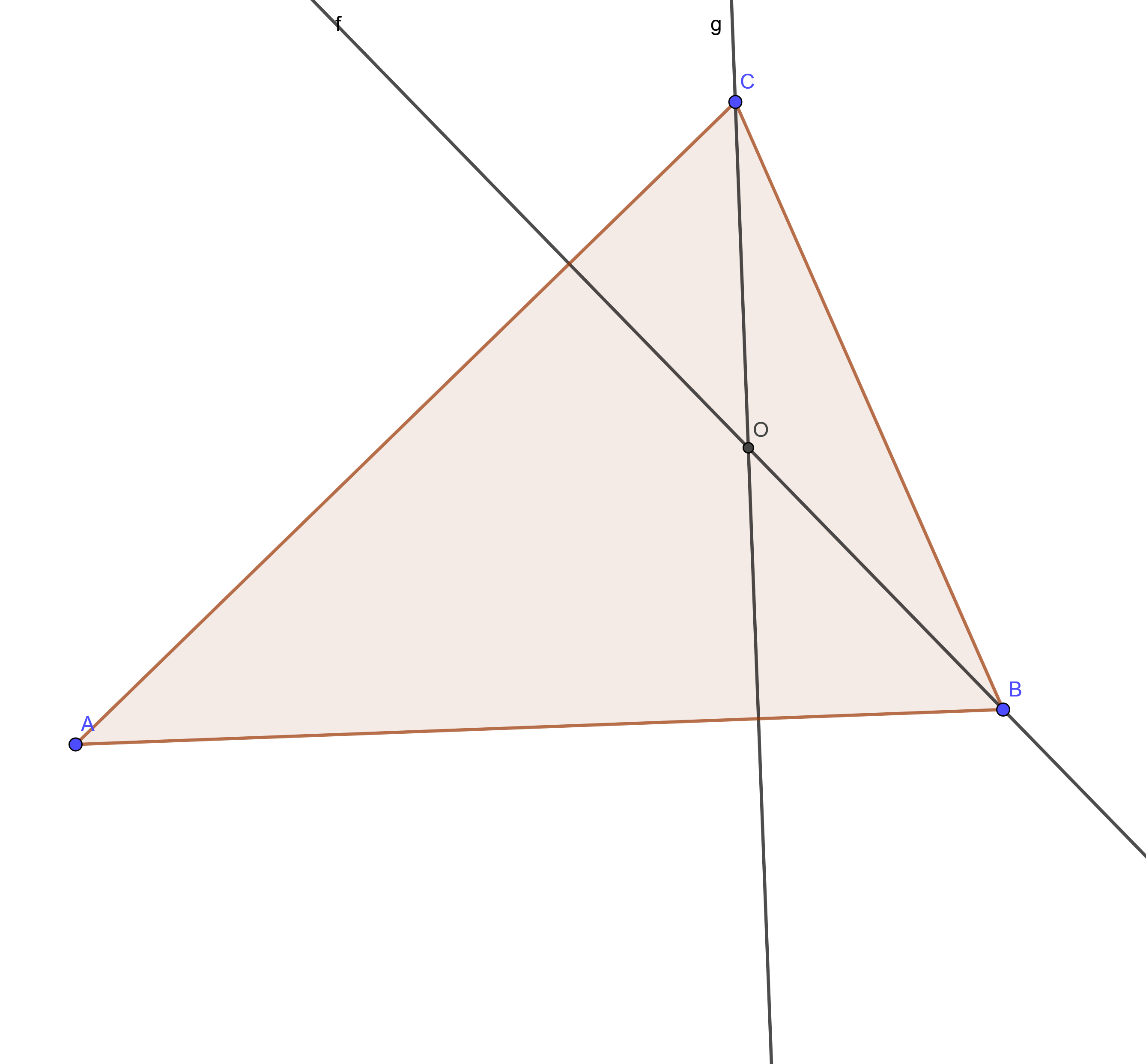
Pour démontrer que les médianes sont concourantes, Daniel propose sur le même modèle $(B+C)\times A+(C+A)\times B+(A+B)\times C=0$.

stfj

Point de concours de médiatrices hyperboliques(d'après l'article de Daniel Perrin et le travail d'Yves Martin)

stfj

Oups : 
Venant de découvrir la géométrie dans ce disque, je ne comprends pas tout. Un peu comme un élève qui manipulerait un logiciel de géométrie dynamique et découvrirait, guidé par son enseignant de nombreuses propriétés sans bien les comprendre. Le (1) de @pldx1 : trouver des résultats. (1)bis : apprendre cette nouvelle géométrie dans un disque, un minimum de connaissances pour (2) trouver des preuves... En tout cas, pour un enseignant de 6è qui doit faire copier la leçon aux élèves : 

"Par un point extérieur à une droite, il passe une parallèle et une seule."

cela est un outil auquel je commence à songer puisqu'il existe au moins une autre géométrie à montrer à ses élèves où ce n'est pas vrai. L'intérêt du résultat précédent est à la fois vivifié pour le professeur. Et les élèves voient l'importance de cette "propriété admise" surtout quand ils auront à l'appliquer dans des exercices de leurs manuels. 

Bonne leçon. N'empêche que tout se passe dans le disque de rayon $1$ et que les seuls points qui m'intéressent pour l'instant sont des points pour lesquels j'ai réalisés des calculs, en l'occurrence $(0.5;0.5)$ et $(0.2;0.6)$. En tant qu'enseignant je veux garder la main sur la machine et savoir ce que je fais.

stfj

Imaginons des lycéens qu'on renoncerait comme Jean Dieudonné le fait dans Algèbre linéaire et géométrie élémentaire à faire travailler implicitement dès la seconde dans un espace affine euclidien $(\mathcal{E},E,v)$ de dimension deux. Ces lycéens ne disposeraient pas de la notation $$\overrightarrow{MN}\text{ pour }M, N\in \mathcal E$$et ne sauraient donc écrire l'égalité fournie par Daniel Perrin dans son article que je détourne de façon éhontée (puisque le but de son article est de dire sagement de faire le contraire de ce que j'imagine ici imprudemment faire)$$\forall O \in\mathcal P, ( \vec{OB} − \vec{OC}| \vec{OA}) + (\vec{OC} − \vec{OA}| \vec{OB}) + (\vec{OA} − \vec{OB}| \vec{OC}) = 0$$
Les lycéens pourraient néanmoins écrire et comprendre sans grande difficulté au moins techniquement que$$\forall A,B,C \in \mathbb R^2 ,( B− C| A) + (C − A| B  ) + (A− B  | C) = 0$$
La démonstration classique fournie par @pldx1 me paraît évidemment bien plus pertinente pour des élèves de lycée. Du seul point de vue d'amateur des mathématiques, la juxtaposition faite par Perrin avec $$(B+C)\times A+(C+A)\times B+(A+B)\times C=0$$est quand même très jolie.

Foys

stfj a dit :
Pour ma part, je ne connais rien* de plus simple, intuitif, naturel, susceptible de généralisations intéressantes, facile à utiliser... en maths que l'objet mathématique $\mathbb R^2$.
_________________________
* Comme tous les matheux de la planète. Désolé d'enfoncer des portes ouvertes.

Tu ne connais pas les autres matheux de la planète et cet avis particulier n'est certainement pas partagé par tous. De façon générale les gens ne trouvent pas intuitives les mêmes choses.

stfj

@Foys, j'ai discuté sur des forums avec des matheux africains, suédois, japonais, australiens, américains, français. Et faire $(2,3)+(4,7)$ ou encore $5.(2,4)$, il y a plus difficile en mathématiques. Je ne comprends pas ton message. Keep It Simple, Student.

nicolas.patrois

Ça dépend comment tu définis l’addition des couples.

Terme à terme (comme les complexes) ? Concaténation (comme les tuples en Python) ? Autre (soyons fous) ?

Vassillia

Je ne sais pas comment se débrouillent les autres matheux mais avec des gamins de moins de 5 ans que je connais très bien (proche ou famille). Je joue sur un carrelage : je demande d'avancer d'un pas, de reculer d'un pas, d'aller d'un pas vers la droite, d'aller d'un pas vers la gauche et naturellement, il reste sur les intersections.
D'abord en faisant comme moi, ensuite en le faisant seul (il suit mes consignes et je suis les siennes).

Ensuite, on peut passer à une combinaison de plusieurs pas dans plusieurs directions et si je veux l'addition, je fais d'abord lui puis moi et on regarde l'ensemble du parcours effectué.

Voilà, j'ai mis $\mathbb{Z^2}$ en intuitif pour le reste de sa vie, le jour où il connaitra les réels, ils transposera son intuition sans problème.

Dom

Vu qu’il est question d’une classe de plus de 20 élèves dont certains ne sont pas des enfants ni des neveux du profs, tous ces exemples me semblent peu pertinents. 

Si c’est pour dire que chaque gamin peut comprendre ça, je suis d’accord. 

Si c’est pour dire que ça peut se faire en classe, non, même si c’est le cas, l’argument ne fait pas mouche, c’est le moins que l’on puisse dire…

stfj

@nicolas.patrois: "Nous allons maintenant définir l'addition des points. Si $A$ et $B$ sont les points, $$A=(a_1,\dots,a_n), B=(b_1,\dots,b_n),$$
alors on définit le point $A+B$ comme celui dont les coordonnées sont : $$(a_1+b_1,\dots,a_n+b_n).$$
Par exemple, dans le plan, si $A=(1,2)$ et $B=(-3,5),$ $$A+B=(-2,7).$$"
Je ne définis rien en maths, je répète ce qu'on m'a appris.

Vassillia

Non, bien sûr qu'on ne peut pas le faire en classe (enfin en maternelle, suivre des consignes de la maitresse de ce genre ne me parait pas impossible à tenter, aucune idée du résultat). Si c'est pas devenu intuitif, c'est parce que l’apprentissage a été loupé (surtout chez les matheux) de mon point de vue. Parler est de l'apprentissage (différent entre chaque pays) et pourtant on pense en phrases, c'est de ça que je parlais, je dirais "en natif" plus que "en intuitif" si tu préfères.

Tu n'imagines pas comme ça marche bien comme jeu, ensuite l'objectif est de se donner des consignes mutuellement pour en partant d'un point, rejoindre un certain point et c'est celui qui donne le moins de consignes successives qui gagne (donc je force à voir la fameuse pente dont je parlais).

Évidemment, je fais souvent exprès de perdre pour encourager (mais pas toujours car il doit aussi apprendre à perdre).

Avancer- Reculer, c'est facile par contre Droite-Gauche, c'est beaucoup plus difficile donc on peut lui mettre un symbole différent dans chaque main pour qu'il s'y retrouve.

Foys

@stfj par exemple dans le bouquin de Dieudonné que tu cites, $\R$ est remplaçable dans la totalité du livre par l'ensemble des réels algébriques (nombres réels solutions d'équations polynomiales à coefficients rationnels) et par exemple il y est impossible de démontrer l'existence de nombres comme $\pi$ ou $e$ (ceci n'est pas un accident mais un choix délibéré de l'auteur; en fait une preuve de l'existence de l'un de ces nombres dans son système entraînerait une contradiction dans les mathématiques élémentaires, bien en dessous de ZFC).

Et on doit pouvoir faire probablement bien pire avec des modèles non standards.

stfj

@Foys : Dieudonné écrit en effet au début du chapitre I :"nous donnons la listes des "axiomes" des nombres réels dont nous nous servirons dans la suite ; il y a d'autres propriétés des nombres réels qui ne peuvent se déduire de ces axiomes (et sont par exemple indispensables lorsqu'on veut fonder axiomatiquement l'Analyse); mais comme nous n'aurons pas à les utiliser, nous ne les mentionnons pas ici." Je n'ai pas compris mathématiquement tout ce que tu as écrit mais je pense que c'est bien loin de l'esprit du livre du professeur conçu par Dieudonné qu'on s'arrête à cela si c'est cela ton propos. Dieudonné propose un programme applicable dès la seconde et je pense qu'il avait en tête le genre de travail élémentaire que propose Lang en 1971 au début de Linear algebra I que tu dois connaître aussi à mon avis. Petit détail : comme je l'ai écrit plus haut pour la démonstration que j'ai proposée du lien entre angle inscrit et angle au centre, je préfère la notation $\varpi$ de Dieudonné à celle usuelle de $\pi$ (voir p. 111)

Dom

Le sujet devient donc (enfin, il l’est devenu depuis un moment) : « que devraient contenir les programmes ? ». 

Bien loin du début… et certains diront qu’ils s’en doutaient déjà…

stfj

Par ailleurs, "bouquin" pour un livre de Dieudonné qu'il a écrit à 58 ans... Cela me fait penser à une anecdote. Un jour, un journaliste demande à Picasso de lui faire un dessin. Picasso gribouille quelques traits en quelques secondes. Picasso demande alors au journaliste : "Combien de temps ai-je mis pour faire ce dessin?"; le journaliste répond : "quelques secondes"; Picasso rétorque : " toute une vie".

Foys

stfj a dit :

Par ailleurs, "bouquin" pour un livre de Dieudonné qu'il a écrit à 58 ans... Cela me fait penser à une anecdote. Un jour, un journaliste demande à Picasso de lui faire un dessin. Picasso gribouille quelques traits en quelques secondes. Picasso demande alors au journaliste : "Combien de temps ai-je mis pour faire ce dessin?"; le journaliste répond : "quelques secondes"; Picasso rétorque : " toute une vie".

Et alors... J'ai dit que j'aimais bien le papelard en question, pour l'exposition d'idées sur ce qui est en fait la théorie des corps réels clos (avec ajout d'un axiome d'Archimède qui n'est utilisé que pour quelques résultats du livre) et pour les provocations de l'introduction, dues au goût immodéré de Dieudonné pour le scandale (mais ça rend la lecture du livre distrayante en tout cas pour moi). Après je ne vais pas jusqu'à partager ton idolâtrie. Personne n'est obligé de faire ça.

stfj

Bien sûr, @Foys

nicolas.patrois

stfj a dit :

"Nous allons maintenant définir l'addition des points.
[…]
Je ne définis rien en maths, je répète ce qu'on m'a appris.

Je souligne.

stfj

@nicolas.patrois : j'ai bien mis des guillemets : c'est extrait de Linear algebra de Serge Lang, traduit par Jean-Marc Braemer et Denis Richard chez interEditions, 1976.

stfj

Je n'ai pas une très grande culture mathématique mais je doute néanmoins, @Foys, qu'on puisse parler de "provocations de l'introduction" d'Algébre linéaire et géométrie élémentaire. Je ne vois pas ce qu'il y a de provoquant dans cette introduction. C'est une analyse froide de technicien des mathématiques. Quand il écrit par exemple : "je tiens L'enseignement de la géométrie de Gustave Choquet pour parfaitement inutile et même nuisible", je pense qu'il se contente d'exprimer librement sa pensée critique de technicien. D'ailleurs, il s'en explique : "quelques mois d'expérience sur le papier quadrillé devraient suffire pour accoutumer l'élève à l'addition des vecteurs , la multiplication par un scalaire et au produit scalaire de deux vecteurs. Dès lors, à quoi bon surcharger sa mémoire de soi-disant "axiomes" qu'il lui faudra s'empresser d'oublier ?" Il joue son rôle : celui du maître d'école qui doit siffler la fin de la récréation du turbulent élève Choquet et suiveurs de toutes sortes.

Je suis également un technicien des mathématiques bien sûr sans commune mesure : je suis en train d'essayer d'écrire une démonstration d'un résultat géométrique simple*, adaptée à des élèves de 6è et je n'y parviens pas. Et pourtant je n'ai pas le choix. Il faut bien confronter les élèves dès la 6è à la difficulté de la mathématique au moins une fois dans l'année. Et je leur ai promis qu'on allait résoudre cette "affaire criminelle mathématique", "trouver le criminel en la personne du principal suspect" : je leur dois la démonstration, c'est mon métier.
_____________
* Soit d une droite et E un point n'appartenant pas à cette droite. Construire au compas seul le symétrique de E par rapport à d. Justifier la construction en utilisant les propriétés du cours, en particulier le cours récent sur le cercle et le cours sur la symétrie axiale.