Enseigner la géométrie en 2023 : quelle place pour l'algèbre linéaire ?
Réponses
-
je m'adresse ici à des collègues, pas à des élèves.
 $(x,y)\mapsto(x-y,x+y)$, c'est bien $(1+i)(x+iy)$, non ? Qu'on puisse associer $(6-2,6+2)$ à $(6,2)$ dès dix ans n'y change rien.
$(x,y)\mapsto(x-y,x+y)$, c'est bien $(1+i)(x+iy)$, non ? Qu'on puisse associer $(6-2,6+2)$ à $(6,2)$ dès dix ans n'y change rien. -
Ok. En tous les cas à des matheux.Mais alors pour parler de 45° aux élèves, que dit-on ?
Et ensuite, pour parler de 63° ? -
Les élèves connaissent tous 90° en rentrant en 6è, la mesure de l'angle droit; et donc 45°, la moitié de 90°. Ce que je leur propose dans l'activité ci-dessus, c'est de constater en mesurant avec leur rapporteur que tous les angles $\widehat{AOA''}, \widehat{BOB''}, \widehat{COC''},...$ mesurent bien environ 45° et que c'est ça une rotation. Quand ils ont compris avec $45°$, rien n'interdit de leur proposer de construire au rapporteur l'image d'une figure simple par une rotation de $63°$. Voire d'utiliser un calque pour cela. $(x,y)\mapsto ( x-y,x+y)$ aura simplement servi à introduire en rendant l'élève réellement actif mathématiquement la notion de rotation. Et au passage pour les meilleurs élèves de comprendre qu'on peut tout transformer en formules qu'ils retrouveront ensuite au lycée. J'ai même la conviction que ne pas montrer le plus tôt possible ces formules simples à des collégiens risque de leur nuire pour leurs études en lycée. Après tout une application linéaire de $\mathbb R^2$ dans $\mathbb R^2$ n'est jamais rien de plus qu'une application de la forme $(x,y)\mapsto ( ax+by,cx+dy)$. Pas de quoi fouetter un chat et pourtant...
-
Justement.Appliquer cette transformation rend actif l’élève (il a quelque chose à faire et admettons qu’il sache le faire). Ok.Mais l’élève n’est pas du tout dans les rotations et ne relie pas du tout cela a une rotation d’angle 45°.Pire encore, la prochaine fois qu’il devra « faire 45°» peut-être appliquera-t-il une autre transformation déjà vue en classe.Ça enlève toute la géométrie.Je ne mets pas cette activité à la poubelle, bien au contraire, mais, je ne suis pas d’accord sur ce qu’elle est censée apprendre.Édit : pour moi, c’est plutôt 1) on connaît ce que signifie rotation d’angle 45° 2) on s’aperçoit qu’avec des calculs tout simples sur les coordonnées, on code cette rotation.
-
ok
 ici avec des rotations d'une maison. Je ne sais pas si c'est le bon sens paysan que j'ai hérité de mes grands-parents paternels, mais faire glisser un objet sur un plan ou le faire tourner autour d'un point, je n'ai jamais ressenti l'intérêt de l'école pour le comprendre, pour l' "apprendre" : cela me paraît évident, intuitif. Par contre pour moi enseigner qu'une rotation d'angle $\theta$, c'est $\begin{bmatrix}\cos\theta & ... \\ ...& ...\end{bmatrix}$, cela relève de ma vision de l'école.
ici avec des rotations d'une maison. Je ne sais pas si c'est le bon sens paysan que j'ai hérité de mes grands-parents paternels, mais faire glisser un objet sur un plan ou le faire tourner autour d'un point, je n'ai jamais ressenti l'intérêt de l'école pour le comprendre, pour l' "apprendre" : cela me paraît évident, intuitif. Par contre pour moi enseigner qu'une rotation d'angle $\theta$, c'est $\begin{bmatrix}\cos\theta & ... \\ ...& ...\end{bmatrix}$, cela relève de ma vision de l'école. -
Je me rends compte à quel point il est difficile de réfléchir à la pertinence d'utiliser telle ou telle voie pour présenter à des élèves des connaissances sur laquelle tant de gens ont réfléchi déjà et se sont forgé une opinion. Il est souhaitable pour alimenter le débat de sortir des sentiers battus.
Imaginons que les transvections apparaissent dans les programmes de collège et qu'il faille initier les élèves à quelques transvections avant qu'elles ne soient vues plus sérieusement au lycée. Pour ma part, il me paraîtrait raisonnable de me limiter dans mon enseignement à une transvection ou deux, telle que $(x,y)\to (x+y,y)$. On pourra trouver l'effet d'une transvection sur une petite usine ici.
-
Parfois on s’est forgé une opinion et il est difficile d’en sortir, c’est vrai. En ce qui concerne l’enseignement (en 2022), il faut peut-être voir ce que cela donne, qui on « atteint », quelle proportion on « atteint ».L’idéal serait, me semble-t-il, de recouvrir toutes les « visions » et pas seulement celle que l’on préfère.S’enfermer dans le calcul pour de la géométrie, cela me semble vraiment peu pertinent. Je reprends l’idée du carré que l’on définirait par {(+-1;+-1)}.Par contre présenter quelques exercices où un lien est fait entre des figures géométriques, des transformations et des calculs, cela m’apparaît pertinent.
-
Je n'ai pas écrit qu'un carré doit être défini par $\{(\mp1,\mp1)\}$ à des élèves. Toujours m'adressant à des matheux, j'ai simplement donné une définition rapide du carré sur laquelle tout le monde s'accorde puisqu'elle s'étend facilement au cube, au tesseract, aux hypercubes. Il serait évidemment délirant de définir le carré ainsi au collège. D'ailleurs je viens de le définir à mes 6è par quadrilatère qui a quatre angles droits et quatre côtés égaux. (C'est très intéressant pour des 6è parce que cela leur permet de comprendre qu'un carré est un rectangle particulier, et de commencer à faire des maths, en prouvant par exemple qu'un quadrilatère qui a 3 angles droits et quatre côtés égaux est un carré...)
-
Ok, je t’avoue que je n’étais plus sûr de rien (nos échanges sont à la fois pro-math et parfois on parle pédagogie tournée vers des élèves, alors l’interprétation n’est pas aisée pour moi).En effet, on peut aussi définir un carré par un rectangle losange. Ça tue le truc dans l’œuf.
Rappelons que l’on utilise des mots pour raccourcir un propos : au lieu de dire « carré », vous pouvez dire « polygone à quatre côtés qui possède quatre angles de même mesure et quatre côtés de même longueur »…Une remarque bénigne : je préfère « côtés de même longueur » ou « côtés de longueurs égales » que « côtés égaux ». C’est accessoire. -
@Dom : je suis tout à fait opposé au fait de définir à des 6è /5è carré par polygone à quatre côtés qui possède quatre angles de même mesure et quatre côtés de même longueur. Ce qui me gêne là-dedans, c'est la prétention de parvenir à convaincre un élève pour qui la notion de carré est évidente qu'il va devoir s'assurer que la définition donnée correspond bien à son intuition depuis la maternelle du carré. Si je comprends bien, tu entends faire démontrer que (1) propriété : dans un quadrilatère, la somme des angles est 360° puis que (2)corollaire: si un quadrilatère a quatre angles égaux, il a quatre angles de 90° autrement dit (3)corollairebis: un carré est un quadrilatère qui a quatre angles droits et quatre côtés de même longueur, autrement dit enfin pour l'élève de 6è/5è qu'il peut considérer la notion de carré apprise à l'école comme une élégante mise en forme de ce que tout le monde connaît, même un enfant de 3 ans. Vues tes visées pédagogiques, tu n'as donc aucun doute sur le fait que tous les élèves d'une classe lambda seront convaincus par cette élégante démonstration. Eh bien, moi, j'en ai. Peut-être ai-je mal compris...
-
Personne ne définit le carré comme ça.Je disais que quand on déplie les définitions ça devient imbitable. Rien que de déplier ce qu’est un polygone…
Pour notre échange j’ai fait exprès de parler des quatre angles de même mesure au lieu des quatre angles droits. Pour l’illustration.Il n’y a qu’en 5e où l’on pourrait s’interroger sur ce détail des angles car on dispose alors du théorème « somme des angles 180° dans n’importe quel triangle ».Pour moi, on doit définir rectangle (quadrilatère avec quatre angles droits), losange (quadrilatère avec quatre côtés de même longueur) puis carré (quadrilatère avec quatre angles droits et quatre côtés de même longueur) et ajouter la remarque « carré = rectangle losange ». -
ok. Mais il faut bien bien définir ce qu'est un carré, au plus tard en 6è. Tout enseignant devra fournir à ses élèves la définition : quadrilatère à 4 angles droits et 4 côtés égaux. N'est-ce pas ? [Si j'ai bien compris, sinon, cela illustre la remarque de @Foys plus haut : "La pédagogie mathématique contemporaine est dominée par l'idée hallucinante qu'un exposé imprécis est plus facile à comprendre qu'un exposé précis, alors même que les mathématiques parlent majoritairement de notions qui n'apparaissent pas dans le monde sensible." Au passage, au cours de ma formation à l'IUFM, je n'ai jamais entendu parler du moindre pédagogue, je ne sais même pas si qui que ce soit se revendique pédagogue en mathématiques. Pour notre discipline, les IREM et le principe de la liberté pédagogique suffisent, non ?]
-
Oui, oui. Ce que j’ai dit en dernier est valable pour des 6e, et même dans le premier degré.Je dis préférer à nouveau « côtés de même longueur » à « côtés égaux ».Je ne vois pas bien le rapport avec la citation de Foys.
-
@Dom :un carré n'apparaît pas dans le monde sensible. Les mathématiques parlent majoritairement de telles notions. Si l'on renonce en classe de 6è à définir précisément un rectangle par quadrilatère qui a 4 angles droits et ne pas démontrer une propriété ou deux telles que (1)un carré est un rectangle particulier; (2)Si un quadrilatère a 3 angles droits, alors c'est un rectangle, ie à montrer l'importance des définitions pour démontrer, ie faire des maths. Bref, si on fait des exposés imprécis sous prétexte qu'on prend des enfants de 6è pour des imbéciles incapables de comprendre le b.a-ba des mathématiques, alors c'est hallucinant. Je n'ai jamais entendu parler de "pédagogie mathématique contemporaine", mais si de tels pédagogues auto-proclamés existent, il faut effectivement les combattre sans relâche.
-
Je ne sais pas ce qu’est le « monde sensible ».
Mais ce n’est pas grave, ce que je propose rentre tout à fait dans ce que tu dis qu’il faut faire, non ?
Où est le désaccord ? (S’il y en a un).
Je dis bien qu’il faut définir rectangle, losange et carré.(1) n’est pas une démonstration, mais plutôt l’application directe de la définition(2) oui, ça c’est tout à fait ce que l’on peut attendre dans le contenu du cours de 6eEn fait je comprends que tu m’expliques ce que veut dire Foys. Je suis d’accord avec ça.
Par contre ça va à l’encontre de ce que tu veux faire dans ce fil « enseigner la géométrie à partir de l’algèbre linéaire » de mon point de vue.Bien malin celui qui souhaite définir les angles (lesquels ?) avant de parler « d’angle droit » à des élèves de moins de dix ans. Pourtant l’algèbre linéaire est le bon outil pour définir ces choses là. Je pense qu’il y a un temps pour tout. Et que l’on ne me fasse pas dire ce que je ne dis pas. Un adepte de cette méthode n’est pas encore présent dans la discussion. Ça ne saurait tarder. -
@Dom : ok je crois que nous sommes en fait d'accord une fois les difficultés de compréhension mutuelle dues à ce support un peu difficile à maîtriser qu'est une communication par messages internet interposés.
 Merci d'avoir fait preuve de patience et de t'être intéressé à mon questionnement : tes réflexions m'ont fait avancer.
Merci d'avoir fait preuve de patience et de t'être intéressé à mon questionnement : tes réflexions m'ont fait avancer. -
C’est une expression philosophique : en gros qui s’oppose au monde des idées, c’est le monde accessible aux sens.Dom a dit :Je ne sais pas ce qu’est le « monde sensible ».
Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
On m'a demandé de préciser le genre d'activité que je propose à des 6è/5è exploitant l'algèbre linéaire. Voici une activité pendant l'étude du chapitre Symétrie axiale en 6è ou Symétrie centrale en 5è dont le but est de montrer qu'alors que l'image du milieu d'un segment par une symétrie est le milieu du segment image, ce n'est pas toujours le cas, par exemple dans le cadre d'une projection centrale. Cette activité s'appuie sur un exposé à des collégiens de Jimmy Dillies sur la géométrie projective que j'ai montré à mes élèves. Pour ceux que cela intéresse, on trouvera ici l'activité :
PS : erratum $M_2=(8,10)$ -
Une anecdote : il y a deux ans, une élève de 3è me demande :"j'ai entendu parler des nombres complexes. De quoi s'agit-il?" Il se trouve que nous travaillions alors pendant l'heure dans un repère $xOy$. Je lui réponds : "ça tombe bien, nous sommes en train de travailler avec des nombres complexes. En fait, ce sont les points du plan. Juste une autre façon de les noter. Par exemple, le point $(0,1)$ est noté $i$, le point $(5,3)$ est noté $5+3i$, le point $(-3,4)=-3+4i$, etc..." Cette élève est très brillante et est aujourd'hui en première au lycée Henri IV à Paris. Quand je l'ai revue l'an passé, elle a apaisé mon inquiétude pour ses résultats en me disant que ses notes en maths étaient de 5 points au-dessus de la moyenne de la classe-ce qu'on a pu vérifier en recevant ses bulletins-, avec cette phrase malicieuse : "c'est facile, tout ce qu'on voit, vous nous l'aviez déjà dit en partie..." Ce qui me gêne, c'est des discussions sans fin sur le sexe des anges avec certains collègues sur le fait de pouvoir ou non écrire que $i=(0,1)$, surtout quand les mêmes collègues ne savent pas par exemple ce qu'est une relation d'équivalence sur un ensemble, notion enseignée naguère en CE2.
-
Ce qui me gêne, c'est des discussions sans fin sur le sexe des anges
D'aucun dirait que ce fil en est une.
-
En effet. Moi non plus je ne trouve pas que l’on pinaille ni qu’on est « rigoriste » dans ce fil.
-
Cette élève est typiquement une élève -et elle est loin d'être la seule- qui, avec une bonne préparation au collège, aurait pu suivre les enseignements d'algèbre linéaire et géométrie élémentaire envisagés par Jean Dieudonné dès 1964 pour des élèves entrant en seconde. Elle devra attendre les cours de mathématiques supérieures et de mathématiques spéciales pour en bénéficier donc ce n'est que partie remise. Ce n'est pas parce que l'enseignement de la géométrie est médiocre et manque d'ambition en 2023 que nos élèves aussi: je doute que ses ambitions s'arrêtent à faire maçon. Pourquoi pas ? J'avais une élève tout aussi brillante il y a quelques années qui voulait devenir cuisinière. En attendant la cuisine, elle apprenait en seconde des mathématiques assez chiadées au lycée Charlemagne.
-
@Dom : je ne me permettrais pas. Je pense à des collègues rencontrés sur un forum de profs de maths, où il m'a été impossible de mener une réflexion sans subir des agressions de la part de collègues objectivement incompétents en mathématiques, ce qui n'est évidemment pas le cas ici.
-
Bonjour stfj,
Parler de dualité projective au collège, cela me semblait un peu ambitieux mais après avoir vu la vidéo, je suis plutôt convaincue donc merci pour le partage.
En ce qui me concerne, je trouve qu'une approche dès le collège qui utilise le calcul avec des coordonnées est plutôt une bonne chose (même si cela ne veut pas dire pour autant faire de l'algèbre linéaire), peu m'importe que ce soit joli ou pas tant que c'est cela qui est utilisé par la suite.
Bien sûr, il ne faut pas perdre au passage l'image mentale qui ferait "voir la géométrie" mais celle-ci ne dépend pas, selon moi, que de la manière dont on a défini telle ou telle notion ni même de l'utilisation de compas ou de rapporteur.Elle se construit surtout par la pratique d'exercices variés, presque indépendamment du prof, même si avec l’expérience, il peut poser les questions qui justement font "voir" les choses, et en cela je trouve les activités de RECLUMATHS et tes exercices plutôt bien pensés notamment les points verts. Je crois que j'aurais tout de même précisé projection sur P' et posé la même question avec une droite parallèle à P.Ceci dit, je n'ai pas vraiment d'expérience sur la manière de présenter la géométrie donc je trouve intéressant de vous lire à ce sujet.In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
@Vassillia : merci
 . Je ne comprends pas ta phrase "je trouve qu'une approche dès le collège qui utilise le calcul avec des coordonnées est plutôt une bonne chose (même si cela ne veut pas dire pour autant faire de l'algèbre linéaire)".
. Je ne comprends pas ta phrase "je trouve qu'une approche dès le collège qui utilise le calcul avec des coordonnées est plutôt une bonne chose (même si cela ne veut pas dire pour autant faire de l'algèbre linéaire)".
Travailler même simplement dans le plan $\mathbb R^2$, c'est faire de l'algèbre linéaire puisque $\mathbb R^2$ est un espace vectoriel réel. Qu'on le taise évidemment aux jeunes élèves en leur disant simplement qu'ils placent des points dans un repère ne change rien à l'affaire pour moi.
Quand on fait faire des translations en ajoutant par exemple le vecteur $u=(3,2)$ à des points $(x,y)$ de $\mathbb R^2$ par $$t_u:\mathbb R^2\to \mathbb R^2, (x,y)\mapsto (x+3,y+2)$$, c'est bien de l'algèbre linéaire -élémentaire oui-, mais de l'algèbre linéaire tout de même.
Qu'on puisse simplement faire faire des transvections, des dilatations, des homothéties, des similitudes ... dès la 6è comme je l'ai montré, idem.
Il m'a semblé au cours de ce post parler d'un peu d'algèbre linéaire tout de même .
.
C'est même tout le propos de mon post. J'ai participé il y a une dizaine d'années à une réunion d'enseignants de mathématiques, d'inspecteurs de mathématiques, et de professeurs des écoles, pendant laquelle un inspecteur était intervenu en disant qu'il fallait restreindre drastiquement les démonstrations en géométrie et privilégier les démonstrations en calcul -avis que je ne partage évidemment pas mais l'avis d'un inspecteur fait force de loi -. J'ai vu dans l'efficacité des méthodes vectorielles pour faire de la géométrie élémentaire, un moyen de pallier à la faiblesse du niveau -en géométrie particulièrement de mes élèves arrivant d'écoles primaires-, pour tenter de sauver ce qui peut l'être et continuer d'enseigner les mathématiques que j'ai toujours aimées, pour lesquelles je suis devenu enseignant; et non de la pisse d'âne... -
On a un élève de 4e sous les yeux.Quel est le contenu du cours sur « voilà une translation » ?
Travailler des exercices avec des opérations sur des couples, me va bien. Mais de quoi parle-t-on vraiment ? -
Certes, il y a de l'algèbre linéaire derrière mais j'avais un peu peur que, pour la partie cours, tu te lances dans le formalisme des espaces vectoriels qui pour le coup me parait vraiment hors de portée d'un collégien lambda. Si ce n'est pas le cas et si tu te contentes d'utiliser des méthodes de calcul, c'est parfait.
In mémoriam de tous les professeurs assassinés dans l'exercice de leurs fonctions en 2023, n'oublions jamais les noms de Agnes-Lassalle et Dominique-Bernard qui n'ont pas donné lieu aux mêmes réactions sur ce forum (et merci à GaBuZoMeu) -
Pour moi, avec ma petite formation mathématique, un point, c'est un couple de nombres. Je ne me gêne d'ailleurs pas pour le dire à mes élèves de 6è. Et au bout du centième couple qu'ils ont placé dans un repère, je doute que cela choque quiconque. Le seul "plan" qui existe, c'est $\mathbb R^2$ ou si l'on veut un plan affine quelconque quelconque de $\mathbb R^3$. Une translation dans $\mathbb R^2$, ie dans "le plan", c'est tout comme dans n'importe quel espace vectoriel réel, une application : $$t_u:E\to E,\quad x\mapsto x+u$$Le lien avec les parallélogrammes est anecdotique. D'ailleurs, qu'est-ce qu'un parallélogramme ? Un quadrilatère dont les côtés opposés sont parallèles ? Mais qu'est-ce que le parallélisme des supports de deux segments ? En quoi cette "définition" donne-t-elle l'occasion de faire faire des mathématiques, ie des démonstrations ? Surtout à l'heure où "les démonstrations en géométrie sont à réduire drastiquement" ? Et puis même qu'est-ce qu'une droite, qu'est-ce qu'un point ? Avons-nous véritablement l'ambition encore de faire comprendre à tous nos élèves de 11 ans que par deux chaises il passe une chope de bière et une seule ? Je n'ai pas cette ambition qui me semble être une hypocrisie en 2023 dans le cadre d'un enseignement pour tous.
Par contre, qu'une droite vectorielle soit $\mathbb R u$, une droite affine du plan $a+\mathbb R u$ où $a,u\in \mathbb R^2$, ça, on peut l'enseigner. Qu'un segment $ab$ soit $\{a+tu\mid t\in [0,1]\}$, ça on pourrait l'enseigner sans problème. Que le milieu d'un segment $ab$ corresponde à $t=\frac12$, ça on pourrait l'enseigner dès le collège et cesser de faire semblant de croire qu'il y ait une quelconque utilité à le "définir" comme "l'unique point $M$ de $(AB)$ tel que $MA+MB=AB$". Alors qu'il s'agit d'une notion affine et non euclidienne.
Pas besoin d'aller à l'école pour savoir ce qu'est faire glisser un objet sans le faire tourner comme sur un périphérique, surtout pas prétendre le formaliser mathématiquement avec des notions bancales, ie rendre compliqué un truc évident, intuitif.
Le but de l'école pour moi n'est pas de faire de la sous-(géométrie d'il y a 2300 ans, ce monument complété par Hilbert) mais d'enseigner qu'une translation, c'est par exemple $$(x,y)\mapsto (x-3,y+7)$$ -
@Vassillia : par exemple pour leur faire faire la translation de vecteur $(\color{red}3,\color{blue}2)$, je leur dis juste : "tu prends le point $(5,7)$ et tu lui associes le point $(5+\color{red}3\color{black},7+\color{blue}2)$. Je travaille en réseau d'éducation prioritaire, je ne suis pas suicidaire

 . Déjà qu'il leur faut globalement un trimestre pour bien placer des points dans un repère, tracer les axes sur les lignes de leurs cahiers, bien compter jusqu'à $5$ pour graduer de $5$ en $5$... Et que les maths ont à peu près autant d'importance à leurs yeux que la musique ....
. Déjà qu'il leur faut globalement un trimestre pour bien placer des points dans un repère, tracer les axes sur les lignes de leurs cahiers, bien compter jusqu'à $5$ pour graduer de $5$ en $5$... Et que les maths ont à peu près autant d'importance à leurs yeux que la musique .... 
-
1) Je comprends le message mais je ne trouve pas la réponse à mes questions : qu’est-ce qu’une symétrie axiale dans le cahier de cours ? qu’est-ce qu’une symétrie centrale dans le cahier de cours ? qu’est-ce qu’une translation, dans le cahier de cours ?Ensuite, une objection :
2) quand je place trois points sur ma feuille, disons A, B et C. Puis que je parle de représenter la droite (AB). En quoi est-ce pertinent de me parler de couples de nombres ?3) Et quand j’ai un pauvre quadrilatère et qu’il n’y a pas de quadrillage et que je dois construire son image par la translation qui transforme A en B ?
qu'est-ce qu’on leur dit ?4) En 6e, a-t-on encore les trois théorèmes sur les droites mettant en jeu des parallèles et des perpendiculaires ?J’essaye de comprendre.
Remarque : oui, un parallélogramme, ça s’appelle parallélogramme pour une raison qui ne m’échappe pas. Au collège, ça me va très bien d’avoir un quadrilatère avec les (supports des) côtés opposés parallèles deux à deux. -
1) Dans le cahier de cours de mes élèves : a) soit $(d) $une droite et $M\notin d$. On dit que $M' $ est le symétrique de $M$ par rapport à $(d)$ au lieu de dire que * $(MM')\perp d$; *$m(M,M')\in d$ (avec traduction en français
 ); b) déf classique également pour $s_O(M)$ ; c) déf classique en 4è avec les parallélogrammes pour la translation.
); b) déf classique également pour $s_O(M)$ ; c) déf classique en 4è avec les parallélogrammes pour la translation.
2) Comme j'utilise beaucoup geogebra en classe, il est facile de montrer aux élèves que même sur feuille blanche, quand on fait apparaître le repère de geogebra ou la partie "algèbre", chaque point est bien associé à un couple de nombres qui permet à l'ordinateur de faire ses calculs. Aussi complexe la figure sur feuille blanche soit-elle.
3) On leur dit bien sûr d'utiliser des parallélogrammes mais pas en 6è, ni même en 5è. Néanmoins dès la 6è, ils auront été familiarisés avec des translations via leur quadrillage.
d'utiliser des parallélogrammes mais pas en 6è, ni même en 5è. Néanmoins dès la 6è, ils auront été familiarisés avec des translations via leur quadrillage.
4) oui, je viens de finir ce chapitre très important.
Mon enseignement de la géométrie à des collégiens est très classique je crois; je veux juste insister sur le fait que l'utilisation des repères est un support parmi tant d'autres (le pantographe ?) qui me semble sous-exploité, témoins les manuels scolaires où ils sont cantonnés dans un chapitre, alors qu'il me semble utile et nécessaire de les utiliser tout le long de l'année. Ma fille qui finit son école d'ingénieur ne connaît ni le cercle à neuf points ni le théorème de Dandelin; par contre, elle a dû assimiler beaucoup d'algèbre linéaire. -
Il ne faut jamais perdre de vue que nos élèves plus ou moins intéressés par notre enseignement sont des êtres en devenir. Quel que soit l'intérêt qu'ils manifestent devant nous, nul doute qu'un jour ou l'autre ils réfléchissent à une partie des divers enseignements reçus : un élève de classes préparatoires réalise qu'il n'a pas entendu parler de translation avant la classe de Terminale, une élève de seconde retrouve la démonstration de l'irrationnalité de $\sqrt2$ vue en troisième, un autre s'interrogera un jour sur la notion de perpendicularité... Le rôle ingrat de l'enseignant de mathématiques est d'armer ses élèves pour ces éventuelles questions qu'ils se poseront un jour, bien après l'enseignement reçu. Dans le cadre de ce fil, je voudrais m'attarder sur la notion de perpendicularité. J'ai parlé de produit scalaire. Même si j'ai très peu enseigné au lycée, je ne comprends pas qu'on l'enseigne autrement , ici ou là, que par $$a_1b_1+\dots+a_nb_n$$
Le fait fondamental pour les calculs des élèves dans diverses situations qu'il s'agit d'une forme bilinéaire symétrique définie positive est alors facile à démontrer, même si au lycée on se contente de parler de propriétés du produit scalaire.
On définit alors la notion de perpendicularité de deux vecteurs en réclamant un peu de patience de la part des lycéens pour montrer le fait non évident que, dans le plan, cette définition coïncide avec la notion intuitive manipulée au collège et à l'école primaire. Puis la longueur d'un vecteur $A=(a,b)$ par $$\sqrt{a^2+b^2}$$ qui cette fois coïncide bien avec la longueur manipulée au collège depuis la classe de 4è grâce au théorème de Pythagore. On est alors en mesure de justifier la définition de la perpendicularité: la condition $\|A+B\|=\|A-B\|$ (représentée sur la figure) correspond à la propriété géométrique suivante : $A$ est perpendiculaire à $B$.
Or, $\|A+B\|=\|A-B\| \iff A.B=0$
J'enfonce sans doute avec l'aide d'éminents algébristes des portes ouvertes... Ici, je trouve que c'est fait correctement, dans le bon ordre contrairement à plus haut.
PS : ma critique s'étend jusqu'à un manuel de 1èS de 1982 de la collection Durrande écrit par A.Thuizat, G.Girault, E.Aspeele et M.Voilquin, où on lit $$\vec{u}.\vec{v}:=\overline{OA}\times\overline{OB'}$$ avec $B'$ projeté orthogonal de $B$ sur $(OA)$. Dans le Nathan 1982, MATHEMATIQUES 1èSE de M.Gourion,C. Lixi et G.Guggenbuhl, par contre on lit: "Nous supposons le plan $P$ orienté et rapporté à un repère orthonormé direct $(O,\vec{i},\vec{j})$. Soit deux vecteurs non nuls $\vec{u}(x,y)$ et $\vec{v}(x',y')$, $$\cos(u,v)=\frac{xx'+yy'}{\sqrt{(x^2+y^2)(x'^2+y'^2)}}$$ $$\sin(u,v)=\frac{\begin{vmatrix}x & x' \\y & y'\end{vmatrix}}{\sqrt{(x^2+y^2)(x'^2+y'^2)}}$$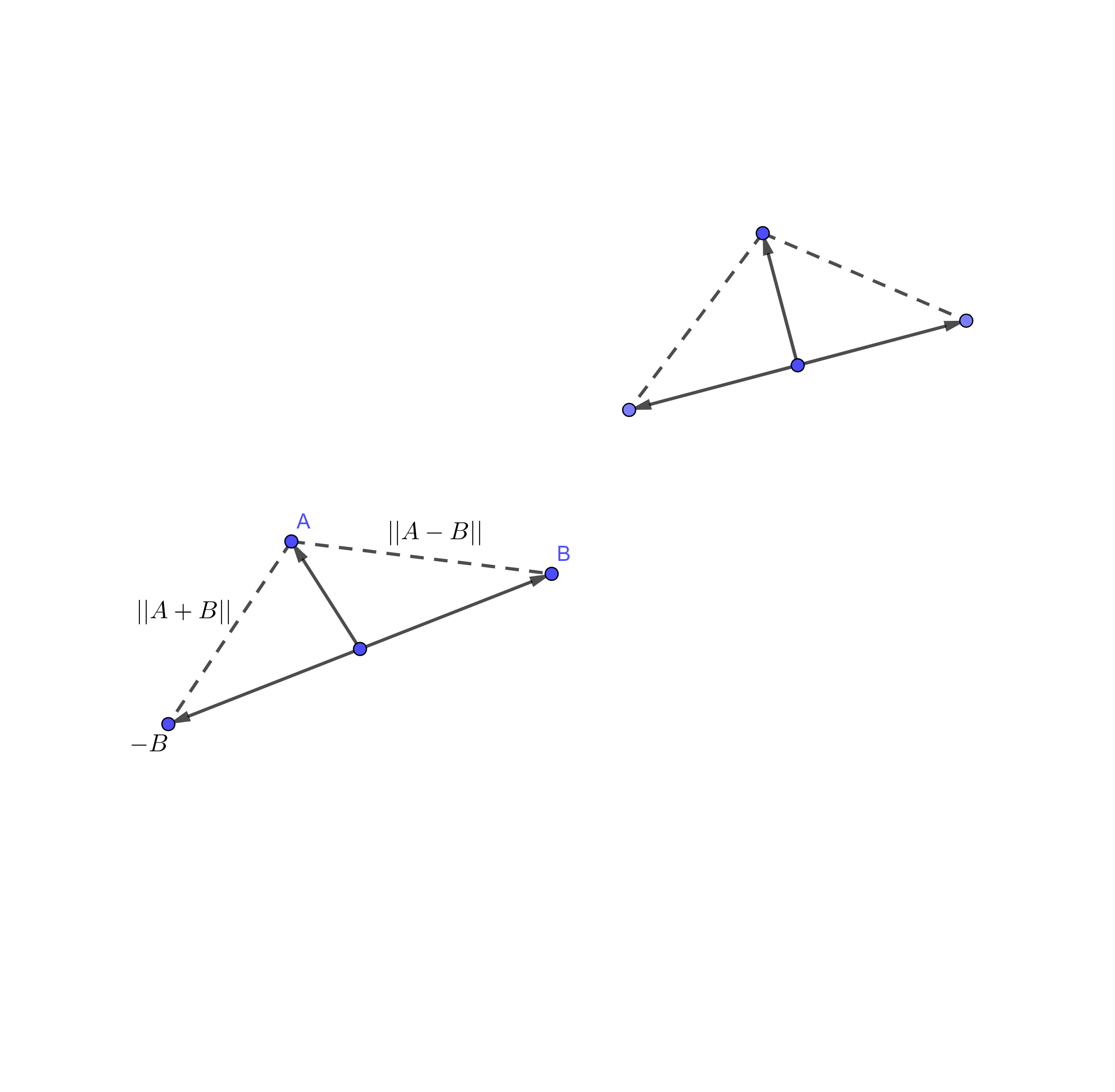
-
@stfj : il me semble que tu introduis, sans le préciser, une notion d'orthogonalité qui dépend a priori du produit scalaire.
-
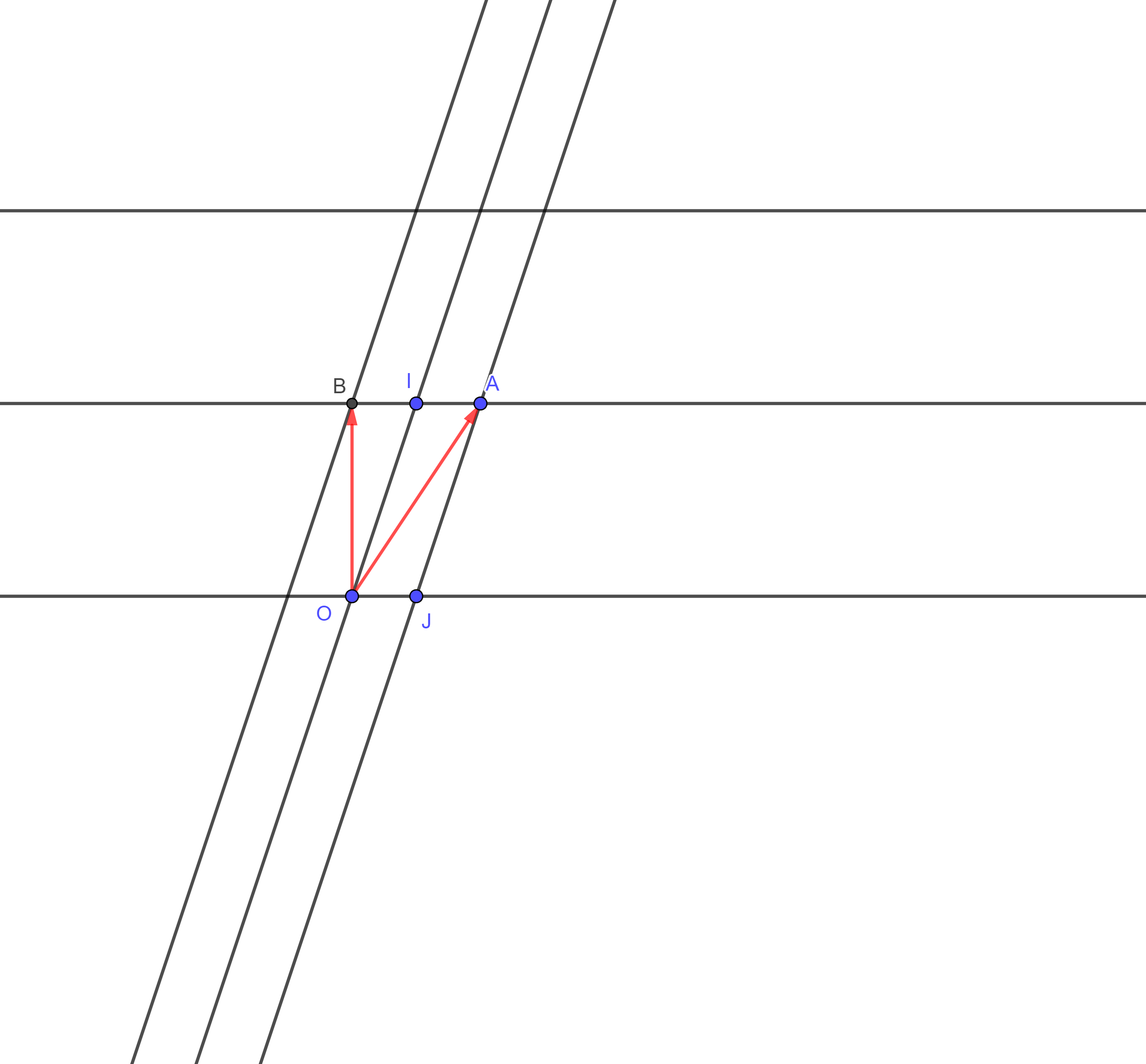
@Magnéthorax : il m'arrive de faire travailler des élèves de collèges dans des repères non orthonormés mais c'est assez rare. Je crois que c'est encore plus rare au lycée où il faut faire en plus des lourds programmes actuels (statistiques, probabilité, arithmétique, géométrie, analyse,...) tout ce qui n'est plus fait au collège. Le but est le suivant : dans la situation classique d'un repère orthonormé, parvenir à convaincre les élèves qu'associer à deux vecteurs identifiés aux couples $(x,y)$ et $(x',y')$ le nombre réel $$xx'+yy'$$va leur permettre de mieux comprendre ce qu'ils ont fait nécessairement de façon plus ou moins intuitive au collège. La notion d'orthogonalité ainsi introduite dépend en effet a priori du produit scalaire, si j'ai bien compris le sens de ta remarque. Soit $J=(1,0), I=(0,1), A=(1,1)$ et $B=(-1,1)$. Alors $IJ=0.AB=0$, autrement dit $A$ et $B$ sont orthogonaux ainsi que $I$ et $J$. Par ailleurs, $I$ et $J$ ont même longueur, ce qu'on vérifie aisément sur le dessin

-
Tiens ! La formule « au lieu de dire » n’est pas mal du tout, je trouve. Ce n’est pas courant mais c’est très explicite et juste à la fois.Pour les définitions, c’est une très bonne idée 😀
1) ok donc pas de mention de couples de points.
Pour le reste je reviens plus tard… -
Prenons la notion simple de projecteur dans un espace vectoriel. Tout le monde s'accordera sur le fait qu'une image mentale dont doit immédiatement disposer l'étudiant qui découvre la notion après son baccalauréat, quand on la lui présente, est celle qu'il aura eu le temps de se forger au cours du collège et du lycée. Or, l'aspect géométrique m'apparaît presque secondaire ici, tellement c'est intuitif ; ce qui me paraît pertinent c'est des écritures (avec abus admis par tous) telles que $\mathbb R^3=\mathbb R^2\times \mathbb R$ ou $\mathbb R^2=(\{0\}\times \mathbb R) \oplus (\mathbb R\times\{0\})$ que l'étudiant aura trop peu rencontrées au secondaire il me semble, si l'on s'interdit en tant qu'enseignant de faire un minimum de théorie des ensembles naïve et d'algèbre linéaire très élémentaire au collège et au lycée. Par exemple, ne pas parler clairement de couple de nombres, de singleton, de paire, de la différence entre une paire et un couple... dès la sixième m'est inacceptable.
Au passage, je rappelle qu'écrire $M=d\cap d'$ pour le point d'intersection de deux droites sécantes $d$ et $d'$ est un abus ; et qu'en toute rigueur, il faudrait écrire $\{M\}=d\cap d'$ et pour le moins, le préciser aux élèves un jour ou l'autre. Comme j'ai un peu de mal en 3è, dans le chapitre probabilité, à ne pas écrire $P(A\cap B )$ pour "la probabilité qu'un événement $A$ se produise en même temps qu'un événement $B$", ce genre de détail appert. -
L’étudiant, même sans avoir rencontré l’idée de projection au collège, n’aura aucun mal à la saisir avec une image mentale de projection telle le soleil ou je ne sais quelle autre idée.Pour l’intersection des événements, le symbole n’a rien de si pertinent. Les mots « et » et « ou » par contre sont à pratiquer inlassablement, me dis-je.
-
Dans un autre fil, le document en lien me paraît très intéressant pour réfléchir à deux points de vue que tout continue a priori à opposer. Même si je dois avouer n'avoir parcouru le texte de Daniel Perrin qu'en diagonale, je comprends qu'il critique [2] Dieudonné Jean, Algèbre linéaire et géométrie élémentaire, Hermann, Paris, 1964. Je cite un extrait de la préface de cette ouvrage de 1964 : "Ce par contre à quoi je suis tout à fait opposé, c'est ce qu'on pourrait appeler "la méthode de l'échafaudage préalable". [...] On voudrait partir d'un autre système d'axiomes, réputé plus accessible, et en déduire ensuite les axiomes de l'Algèbre linéaire." En tant qu'enseignant en exercice, je n'éprouve nul besoin qu'on vienne m'expliquer la cohérence de ce que j'enseigne : mes connaissances en algèbre linéaire me suffisent pour cela. Et je pense que préparer le collégien avec quelques connaissances très élémentaires d'algèbre linéaire serait bienvenu.
-
Pour "paraphraser" le début de la présentation de l'article: Ce texte s'adresse évidemment aux professeurs et pas du tout aux élèves :
* Un point est un couple de nombres $(a,b)$; par exemple $(5,3)$ est un point;
* Le plan $\mathcal{P}$ est l'ensemble de tous les points, autrement dit l'ensemble de tous les couples de nombres.
* Axiome. (I) Par deux points distincts du plan passe une droite et une seule. (on remarquera qu'il s'agit d'un théorème en algèbre linéaire)
* Définition. Soient $d, d'$ deux droites de $\mathcal{P}$. On dit qu’elles sont parallèles si elles ont même direction $(u)$.(remarque : il y a la notion de droite vectorielle dirigée par $(u)$, où $u$ est un élément de $\mathcal{P}$, une droite de direction $\mathbb R u$ étant définie comme une partie de la forme $a+\mathbb R u$, où $a\in \mathcal {P}$.
* théorème (admis pour les élèves de collège comme beaucoup de points qu'ils peuvent aisément vérifier dans un quadrillage) : Soit $d$ une droite et $a$ un point non situé sur $d$. Il existe une unique droite parallèle à $d$ passant par $a$.
* théorème : La relation de parallélisme est transitive.
* [...]
* 3.1 Homothéties On aura besoin de la notion d’homothétie, mot savant pour l’opération d’agrandissement-réduction. 3.1 Définition. 1) Soit $O$ le point $(0,0)$ et $k$ un nombre. L’homothétie de centre $O$ et de rapport $k$ est l’application de $\mathcal{P}$ dans $\mathcal{P}$ qui à un point $M$ associe le point $kM$. (remarque : les homothéties vectorielles sont bien suffisantes au collège.)
Attention, ce texte a été écrit très rapidement et il recèle sans doute de nombreuses coquilles, imprécisions, maladresses, voire des erreurs plus graves.
-
Pour la géométrie (axiomatique) d'incidence, voir le livre d'Emil Artin: "algèbre géométrique".
Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
La dernière fois que j'ai eu Algèbre géométrique entre les mains, c'était il y a environ trente ans. Lang part de $\mathbb R^2$ dans Linear algebra et Lang était un élève d'Artin.
-
Voici un exercice que je pense faisable en 3è/2nde(il y a une part de provocation mais l'idée que je veux discuter est là). Dans $\mathbb R^2$ euclidien canonique, soit $A=0,B=6i,C=8,P=5i,R=20, d=(PR)=P+\mathbb R (R-P)$ et $Q=d\cap (BC)$ 1. En appliquant le théorème de Ménélas, prouver que $\frac{\overline{QC}}{\overline{QB}}=-3$; 2. En utilisant le théorème de Thalès, en déduire que $H$, le projeté orthogonal de $Q$ sur la droite réelle est $H=\frac14C$
-
Vraie question : on voit, officiellement, le théorème de Ménélaüs au collège maintenant ?
-
@stfj
Un élève de troisième/seconde va simplement chercher les deux équations de droites avec la méthode de son cours puis résoudre le système pour trouver l'abscisse du point d'intersection, non ?Toi qui est fan d'algèbre linéaire, tu ne devrais pas avoir envie qu'il fasse autrement, si ? -
@JLapin : tu as raison. N'empêche que l'exercice est intéressant pour vérifier le théorème de Ménélas en Terminale Spécialité, non ?
-
Il serait temps de faire la différence entre Ménélaüs, mathématicien d'Alexandrie à la fin du premier siècle, et Ménélas, roi mythique de Troie, de nombreux siècles auparavant.
Cordialement. -
Cela porte confusion entre le théorème de Ménélaüs (le mathématicien et astronome) et le théorème de Ménélas (le roi légendaire).
-
Ménélas(Μενέλαος / Menélaos : « qui soutient le peuple ») est un prénom grec qu'ont en commun le mathématicien-astronome, le roi légendaire et le frère de Ptolémée I. Il n'y a pas de théorème du roi légendaire ni du frère de Ptolémée et donc pas de risque de confusion. Dire "théorème de Ménélaüs" n'est donc que céder à la pratique usuelle, dominante, ce qui relève de la liberté de chacun.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.2K Toutes les catégories
- 9 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 63 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 313 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 773 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres





