Enseigner la géométrie en 2023 : quelle place pour l'algèbre linéaire ?
Réponses
-
En fait à gros traits, les transformations au collège sont du « on voit que ». Ça rappelle plutôt l’école primaire.Pourquoi pas. On en est là, c’est comme ça.Mais au bénéfice de quoi d’autre ?Si ce fil est pour dire : enlevons ça [la géométrie de papa] complètement et faisant du calcul avec vecteurs, couples, matrices, à la limite je comprends la demande. Et on peut donner des représentations de ces calculs dans un repère. Ça d’accord.Mais si c’est pour dire « enseignons la géométrie avec l’algèbre linéaire », je pense que c’est un leurre car la géométrie doit se faire [selon moi] avec énormément de représentations (triangle, rectangle, etc.) avant de s’attaquer à ses formalismes.
-
Dom a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2403437/#Comment_2403437[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]C'est effectivement ce que je constate chaque année depuis des décennies. D'où l'importance d'y consacrer beaucoup de temps, d'insister sur des notions presque métamathématiques telles que les nœuds des quadrillages, les lignes verticales du cahier, les lignes horizontales (les nœuds étant leurs intersections), d'apprendre à compter les lignes plutôt que les carreaux, d'utiliser un vocabulaire qui "parle" (je parle de l'"axe tour Eiffel" et de l'"axe horizon"). On a le temps, on n'est qu'en 6è ou 5è et c'est l'un des objectifs des programmes qui a pour intitulé SE REPÉRER. Quand j'étais enfant, je crois que c'est la seule difficulté que j'ai éprouvée à l'école primaire en maths : on me demandait de décaler une figure de $\color{red}7$ carreaux vers la droite et je ne comprenais pas bien : cela aide de disposer de $(x,y)\to(x,y)+(\color{red}{7},0)$ en commençant par des exemples tels que $(5,3)+(\color{red}7,0)$ ou $(5+\color{red}7,3)$ appuyés sur un quadrillage.[Gustave Eiffel (1832-1923) prend toujours une majuscule. AD]
-
Oui @rebellin, il y a même un gros bug dans le programme de maths expertes. En géométrie dans le plan complexe, on demande d'interpréter l'argument d'un nombre complexe non nul, alors qu'il n'est jamais fait mention d'angle orienté de vecteurs dans les programmes du secondaire !
Bon, ça me donne l'occasion d'en parler à mes élèves qui suivent cette option.
-
gai requin,
Je pense que c’est juste parce que pour tout le monde le cercle trigonométrique se regarde de la même façon, la mesure de l’angle $\theta$ se regarde en partant de l’axe des abscisses et en tournant dans le sens trigonométrique jusqu’au deuxième côté de l’angle considéré (on déroule le cercle, on enroule la droite, etc.).Dans ce sens, l’interprétation de l’argument, ce n’est que ça.Faut-il une théorie « angles orientés de vecteurs » pour cela ? Peut-être. Il y a discussion.
Mai en fait, c’est la suite du « on voit que » du collège.D’un certain côté, tous les matheux (non ?) qui veulent retrouver certains formules basiques de la trigonométrie griffonnent le cercle trigonométrique, appelle $x$ la mesure de l’angle et ne font que considérer cette vision de l’argument. Ils le font aussi mentalement (je pense à $\cos (\pi+x)=-\cos (x)$ par exemple). -
C'est tout à fait cela que je pense. Par contre, je ne vois pas en quoi c'est un leurre. Il y a quarante ans, on m'enseignait que l'image d'un segment par une symétrie orthogonale est un segment de même longueur. Aujourd'hui, j'enseigne en 6è que l'image d'un segment par une symétrie axiale est un segment de même longueur. Et en outre, je dispose de la transvection $(x,y)\to(x+y,y)$ pour montrer aux élèves que ce n'est pas toujours le cas, qu'il existe des applications du plan dans lui-même qui transforment un segment en un segment de longueur différente, tout comme mon collègue d'il y a quarante ans devait disposer de tels exemples.Dom a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2403543/#Comment_2403543[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]
-
Il suffit de parler des affinités orthogonales pour trouver de tels exemples 😏
Au fait, on a donc obligatoirement un quadrillage en géométrie ? -
Ha…Mais alors si on a un triangle sur fond blanc et une droite, qu’est-ce qu’on fait pour représenter le symétrique du triangle par rapport à cette droite ?
une remarque : les élèves s’en sortent plutôt mieux sur feuille blanche à main levée (même si c’est brouillon, oui, oui) que sur quadrillage. Dis-je une bêtise ? -
@Dom : au collège, l'utilisation de l'équerre est problèmatique, encore plus depuis les générations COVID : il faut leur apprendre à manipuler l'équerre mais d'autres supports sont aussi nécessaires : en 6è, les programmes invitent à l'utilisation du papier calque, du pliage , on peut utiliser des découpages de figures et je trouve très efficace l'utilisation des repères par exemple la symétrie par rapport à la première bissectrice $(x,y)\mapsto (y,x)$ ou encore la similitude indirecte $(x,y)\mapsto (x+y,x-y)$ après avoir évidemment consacré beaucoup de temps au repérage. Tous les angles d'attaque sont les bienvenus vues leurs difficultés. Le seul recours au dessin sur papier blanc n'est pas conforme aux programmes.
-
Tiens, cette dernière phrase m’intrigue.Enfin, « le seul », certes ! Mais « le recours au papier blanc » reste conforme.Du coup, « le seul recours au repérage » n’est pas conforme non plus, il me semble.Tu as parfaitement [raison] : l’équerre c’est la plaie. Et même avant covid.Pour ton idée avec les coordonnées, comment t’en sors-tu avec une droite qui ne serait pas sur le quadrillage (tracée « au hasard » ou disons avec un coefficient $\pi$ ou un truc aussi pourri) ?
Et ne serait-ce que pour une droite portée par le vecteur (3;7), comment fait-on ? -
D'ailleurs petite remarque : familiariser les élèves le plus tôt possible avec la symétrie $(x,y)\mapsto (y,x)$ n'est pas du luxe. Combien d'élèves de lycées sont capables de comprendre pleinement que pour une fonction $f:\mathbb R\to \mathbb R$ bijective, le graphe de $f$ et celui de $f^{-1}$ sont symétriques ? (car $y=f(x)\iff x=f^{-1}(y)$). Combien d'élèves de lycées font la distinction entre une paire et un couple? A force de s'interdire de faire un minimum de théorie des ensembles naïve et d'algèbre linéaire - dans l'exposé à des lycéens sur la géométrie projective, Claire Voisin commence par rappeler qu'on lui a dit qu'il fallait éviter de parler d'ensemble et ne cesse avec malice ensuite d'en parler aux lycéens pendant son exposé -, ne risque-t-on pas d'avoir des élèves non seulement faibles en géométrie mais aussi en analyse ?
-
C’est un autre sujet.Je suis pour qu’on écrive déjà au collège quelques ensembles avec des accolades. Ça ne mange pas de pain et c’est utile pour la suite. Notamment toutes les questions simples que doivent gérer les profs de L1 comme {1;1;2} contient deux éléments etc. seraient déjà traitées. Ce ne serait pas du luxe.Bon, d’ailleurs, on est très très loin de « la théorie » des ensembles.
-
@Dom : comme le dit le programme il faut multiplier les procédés pour faire faire de la symétrie aux élèves (pliage-découpage, pliage-calque, utilisation des repères, de geogebra, utilisation des instruments de dessin, animations comme ici...) Je me limite en ce qui concerne l'utilisation des repères à $(x,y)\mapsto (y,x), (x,y)\mapsto (-x,y)$ ou à la similitude indirecte $(x,y)\mapsto(x+y,x-y)$, bref ce que les élèves peuvent mettre en pratique très rapidement sans qu'aucune difficulté n'apparaisse (ce n'est vraiment pas le but au contraire).
-
En ce qui concerne les angles, ie les rotations, je ne comprends pas qu'on n'utilise pas très tôt des similitudes directes telles que $(x,y)\mapsto(-x,-y)$, $(x,y)\mapsto (-y,x)$ (rotation de $+\frac{\pi}{2}$) ou $\begin{bmatrix}0 & 1 \\-1 & 0\end{bmatrix}$ (rotation de $-\frac{\pi}{2}$), ou $\begin{bmatrix}3 & -4 \\4 & 3\end{bmatrix}$: c'est facile à mettre en œuvre dès la 5è : j'ai fait étudier récemment à des classes de 5è l'angle de $+\frac{\pi}{8}$ via la similitude directe $(x,y)\mapsto (x+y,x-y)$ sans rencontrer de difficultés majeures : il est vrai que seuls les deux-trois élèves les plus avancés dans une fiche d'exercice ont traité l'exercice mais je n'ai pas la prétention d'enseigner $+\frac{\pi}{8}$ à des fainéants qui n'ont même pas une règle.
-
Bon, je te trouve quand même un peu déconnecté (certes ça semble gratuit… je m’en veux déjà).Je propose à nouveau l’argument au sujet des dyslexiques ou dyscalculiques. Ça ne représente pas beaucoup, peut-être, mais ça illustre le problème de tous ces symboles que tu souhaites ajouter.On a déjà des problèmes à distinguer AB de (AB) de [AB) etc.
Autre argument plus général : voir la géométrie comme des nombres (le carré plus haut avec ces accolades… ) c’est effacer toute la géométrie. -
@Dom : Oui mais l’idée en maths expertes, c’est de faire des maths.
-
Le problème de distinguer AB de (AB) de [AB) etc. est vite résolu : les élèves qui ne veulent pas faire l'effort d'apprendre n'ont qu'à faire des phrases en français comme la plupart des matheux que je lis qui écrivent "la droite AB, le segment ab, la demi-droite d'origine A passant par B..." : il semble que même les mathématiciens professionnels n'aient pas fait l'effort d'adopter ces conventions parenthèses-crochets. Alors pourquoi s'époumonner à les attendre d'élèves qui souvent ne prennent même pas la peine d'avoir une règle en cours de maths ?
-
" il est vrai que seuls les deux-trois élèves les plus avancés dans une fiche d'exercice ont traité l'exercice mais ..."Fermez le ban.
-
Prétendre enseigner des mathématiques de 6è à un dyscalculique, c'est comme prétendre apprendre le chinois à un perroquet croate, non ? A l'impossible, nul n'est tenu, pas même un fonctionnaire.
-
Nostalgie...Moi aussi j'ai aimé ce livre https://archive.org/details/algebrelineairee0000dieu/page/n3/mode/2upAprès je me demande ce que ça peut donner si on tente ça devant les petites classes. Par contre je pense que les enseignants et autres matheux mûrs devraient le lire car il est vraiment instructif (il trivialise proprement beaucoup de choses).Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$.
-
Je suis d’accord gai requin, le lycée c’est tout de même un niveau où on devrait arrêter de bricoler.stfj,
Je comprends mieux ton point de vue
en 2022 les profs de collège doivent enseigner à tous les élèves et toi tu n’as pas envie ou tu ne trouves pas cela pertinent.
La phrase relevée par Gérard, ton propos sur les dyscalculiques (d’ailleurs erroné, pour ma part car confondre Math et calculs est de mon point de vue une grave erreur) et enfin la fin de la phrase sur « des fainéants » (désignant des élèves) illustrent bien que tu n’as pas envie de te prendre la tête avec les élèves qui ne suivent pas.Ça s’entend. Mais en 2022, ce n’est pas cela être enseignant au collège, il me semble.Je ne juge pas j’ai aussi du mal avec plein de choses. -
Grosso modo, on plonge tout espace affine de dimension $n$ dans un espace vectoriel de dimension $n+1$ pour avoir la trivialisation de @Foys. Au collège ? 😉Puis on prend le projectivisé de cet espace vectoriel pour se lancer dans la géométrie algébrique. Au lycée ? 😉
-
Les gens qui ont détesté lesdites "maths modernes" font essentiellement partie du monde enseignant. La plupart des élèves aimaient, même ceux qui n'ont pas fait de carrière scientifique. La pédagogie mathématique contemporaine est dominée par l'idée hallucinante qu'un exposé imprécis est plus facile à comprendre qu'un exposé précis, alors même que les mathématiques parlent majoritairement de notions qui n'apparaissent pas dans le monde sensible.La fabrique de la réalité est aussi faite de blessures narcissiques. En l'espèce l'évolution de l'enseignement des mathématiques après 1980 est une gigantesque vengeance, venant de profs qui se sont vus imposer cette réforme sans formation préalable, qui ne comprenaient pas grand chose et qui n'allaient pas reconnaître que, que l'on le veuille ou non, les maths modernes avaient raison sur les fondements et la nature de maths. Mais c'est la société qui subit le coût de cette vengeance (les maths sont devenues réservées à quelques Parisiens et aux enfants de chercheurs en maths).Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$.
-
Soit @stfj trolle, soit il est complétement déconnecté de la réalité et je plains les pauvres jeunes âmes qu'il reçoit en classe.
-
« Les gens qui ont détesté lesdites "maths modernes" font partie du monde enseignant. La plupart des élèves aimaient, »
Foys, d’où ça sort ? Cette phrase est évidemment fausse. Tu vas trouver énormément de gens qui ont détesté les maths modernes et qui n’ont rien à voir avec l’enseignement.Quant à « la plupart des élèves aimaient », ça m’inquiète :
que ce soit vrai ou faux, dès qu’on avance « les élèves aiment » comme argument, je fuis la discussion. Pour moi on n’a pas à tenir compte de l’avis de celui qui apprend. Et surtout quand il est mineur. -
Dom a dit :« Les gens qui ont détesté lesdites "maths modernes" font partie du monde enseignant. La plupart des élèves aimaient, »
Foys, d’où ça sort ? Cette phrase est évidemment fausse. Tu vas trouver énormément de gens qui ont détesté les maths modernes et quiJe parle de mon entourage. Des gens qui ont été artistes, architectes, comptables, qui ne sont pas matheux et se définiraient même comme non matheux. Des gens qui carrément se vantaient "de détester les maths mais d'avoir aimé les maths modernes" (oui c'est bizarre mais possible, l'individu en question n'ayant pas continué sa formation en maths au point de faire le lien).Après les anecdotes personnelles ne font pas les généralités certes mais je me demande pourquoi le tableau partiel que je découvre au cours de ma vie ne correspond pas à la description apocalyptique des détracteurs de cette réforme.Une fonction est un ensemble $f$ de couples tel que pour tous $x,y,z$, si $(x,y)\in f$ et $(x,z)\in f$ alors $y = z$. -
@gai requin : les idées exposées par Dieudonné dans Algèbre linéaire et géométrie élémentaire sont limpides. Son livre s'adressait aux enseignants de lycées les plus à même de mettre en oeuvre ses propositions . Il propose non des exercices mais des thèmes d'exercices, libre aux enseignants de développer autant que nécessaire pour s'adapter à leurs publics. Ce sont peu ou prou les mêmes idées qu'on trouve par exemple chez Serge Lang exposées très clairement au début de Linear algebra et ensuite développées tout le long des deux tomes avec le talent pédagogique bien connu de Lang. Comme je l'ai écrit plus haut, Alfred Doneddu dans Compléments de géométrique algébrique (1972) n'envisageait pour son cours de maths sup et spé comme espaces affines que ceux associés à un espace vectoriel $E$, ie $(E,E,v)$ avec $v:E\times E\to E, (a,b)\mapsto b-a$. Donc les espaces affines généraux non. Juste travailler dans les espaces vectoriels réels $\mathbb R^2$ ou $\mathbb R^3$ ou le $\Z-$module $\Z^2$. Dans son célèbre cours de mathématiques pour le premier cycle universitaire, Dixmier en abordant les espaces affines dit que cela risque de paraître compliqué aux lecteurs et a peu d'importance pour la suite.
En substance se limiter à $\R^2$ jusqu'en Terminale. -
Comment se fait-il que des messages sont publiés en plusieurs exemplaires ? Cela rend la lecture du post assez désagréable. Le livre de Dieudonné a l'air intéressant, mais il semble malheureusement introuvable sauf d'occasion. Il n'a pas été réédité ?
Je n'ai pas d'avis sur le sujet, mais je trouve exagéré de dire de stfj qu'il est déconnecté de la réalité alors qu'il fait des propositions qu'il tente d'expérimenter en classe. -
il est vrai que seuls les deux-trois élèves les plus avancés dans une fiche d'exercice ont traité l'exercice mais je n'ai pas la prétention d'enseigner $+\frac{\pi}{8}$ à des fainéants qui ,n'ont même pas une règle.
Je ne trouve pas ça exagéré, moi, de dire qu'il est déconnecté de la réalité.
De plus, ses propositions dépassent même ce qui s'est fait dans les années 70 et ce fut déjà un échec cuisant (ce que je déplore). Fort de ces faits, il serait bien de réévaluer la proposition de @stfj. Je ne dis pas que tout est à jeter, bien au contraire. Il serait même, selon moi, intéressant de revenir aux mathématiques modernes au lycée dans les classes qui se veulent scientifiques, mais, il faudrait clairement arrêter de vouloir faire ça au collège. Ça n'apporte rien. Le maçon du coin n'a pas besoin de comprendre la notion de bijection ni même comment fonctionnent sous le capot les isométries du plan ou de l'espace. En revanche, il lui sera beaucoup plus utile de savoir faire des calculs, proportions et autres changements d'unités, tout en étant capable de se servir du théorème de Pythagore.
-
Dom a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2403584/#Comment_2403584[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]Je connais bien un dyspraxique, il est très à l'aise comme utilisateur de logiciels de géométrie, et particulièrement de GeoGebra qu'il a beaucoup pratiqué, il est également à l'aise avec AUTOCAD (l'habileté à manipuler ce type de logiciel est partagée par les dyspraxiques)Il n'est par contre pas à l'aise avec l'écriture de l'algèbre (exemple confusion entre $y(y+1)$ et $y\times y + 1$). Pour représenter ces deux expressions les informaticiens utilisent des arbres à la manière dont procède un compilateur. C'est en utilisant des arbres qu'il fait du calcul algébrique. L'ennui c'est que s'il écrit de l'algèbre avec des arbres lors d'examens type BAC, il va se faire sanctionner !
-
@Barry : merci. Ce que je raconte brièvement ici est le fruit de 25 ans de pratique professionnelle : toutes les activités que j'évoque ont été testées, certaines fonctionnent, d'autres moins. Et vus les publics de 2023, il est clair qu'une activité qui fonctionne mal, je ne suis pas un héros pour la maintenir très longtemps en classe... Donc en gros les activités que j'évoque fonctionnent. Quant aux difficultés réelles d'utilisation des repères mentionnées par @Dom, je les connais et consacre beaucoup de temps en classe pour y remédier puisqu'ensuite c'est beaucoup utilisé, conformément à ma liberté pédagogique.
-
Je ne vois pas pourquoi il faudrait revenir aux maths modernes ou enseigner l'algèbre linéaire pour faire de la géométrie déductive accessible dès le collège. Il n'est pas non plus nécessaire de lister tous les axiomes d'Hilbert.
Il suffit de partir des briques de base que sont "le parallélisme, l'angle et la longueur" et d'admettre quelques (très peu en fait) propriétés fondamentales comme les égalités d'angles (alterne-interne, correspondant, etc.) A partir de là on peut très vite se lancer dans des démonstrations élémentaires.
Entre l'époque maths modernes et l'époque actuelle, il y a quand même eu une bonne décennie où on a fait des maths "traditionnelles" relativement rigoureuses. -
L'ennui c'est que les dys ne sont pas à l'aise avec les conventions typographiques de l'écriture de leurs livres. Si on leur présente les mêmes idées avec des figures alors ils comprennent et se réconcilient avec les mathématiques qui ne représentent plus pour eux un codex abscons !stfj a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2403605/#Comment_2403605[Inutile de recopier un message présent sur le forum. Un lien suffit. AD]
-
@Cyrano : je te propose si tu veux bien le petit test suivant dont j'ai parlé plus haut . Soit $A$ et $B$ deux points du plan et $d$ la médiatrice de $[AB]$. Soit $M$ un point du demi-plan contenant $A$. Comment démontres-tu en 5è (disons en admettant (1) qu'un point appartient à la médiatrice d'un segment ssi il est équidistant des extrémités et (2) l'inégalité triangulaire) que $MA<MB$ ?
-
@stfg : Cela dépend comment tu as défini la notion de médiatrice. Pour certains c'est l'ensemble des points équidistants de $A$ et $B$. Auquel cas ta première proposition est vraie par définition. Si tu définis la médiatrice comment étant la droite perpendiculaire à $[A,B]$ passant par le milieu, alors il suffit d'appliquer Pythagore de chaque côté pour voir que les deux distances sont les mêmes.
Quant à l'inégalité triangulaire, elle se démontre aussi par Pythagore en traçant la hauteur du triangle.
-
@Cyrano : définissons la médiatrice comme l'ensemble des points équidistants de $A$ et de $B$. On est en 5è donc les élèves ne connaissent pas le théorème de Pythagore. Je propose donc d'admettre l'inégalité triangulaire.Soit $M$ un point du demi-plan contenant $A$. Comment démontres-tu que $MA<MB$ ?
-
@stfj Simple question... combien de tes élèves de cinquième comprennent ? Combien y arrivent ? Trois ? Comme pour les similitudes plus haut ? Mais c'est pas grave parce que les autres ce sont des branleurs qui ne ramènent même pas leur règle donc on peut les abandonner sur le bord de l'autoroute mathématique ?
-
@dp : Je ne vois vraiment pas ce qu'il y a d'étonnant à écrire qu'un élève qui vient fréquemment en cours de géométrie sans même une règle risque fort de ne pas profiter beaucoup des enseignements dispensés. Quand de tels élèves accumulent des retards, difficultés diverses et variées, la seule chose dont on puisse se soucier c'est les nuisances que ces cancres risquent d'apporter, n'est-ce pas?
-
Ce que je trouve étonnant c'est de les abandonner et de le crier ouvertement sur les toits, surtout… Aussi, peut-être est-ce parce qu'ils ne comprennent rien à ton charabia élitiste qu'ils agissent de cette façon, non ?
-
Pourtant, tu enseignes en sixième et en cinquième. Je ne sais pas si je suis naïf, mais si j'étais enseignant à ce niveau j'essaierais plutôt de faire aimer les mathématiques à toute la classe au lieu d'être élitiste et m'occuper uniquement des trois meilleurs qui n'auraient de toute façon pas besoin de moi pour réussir. En tout cas bravo, grâce à toi les bancs des universités seront moins encombrés !
-
Hélas non. Les bancs seront autant encombrés 🤣
-
Un peu moins tout de même ! 30 étudiants de moins chaque année ! Il a trouvé comment résoudre le problème ! Que chaque prof fasse pareil, et d'ici la fin de la décennie plus de soucis de budget à l'université !
-
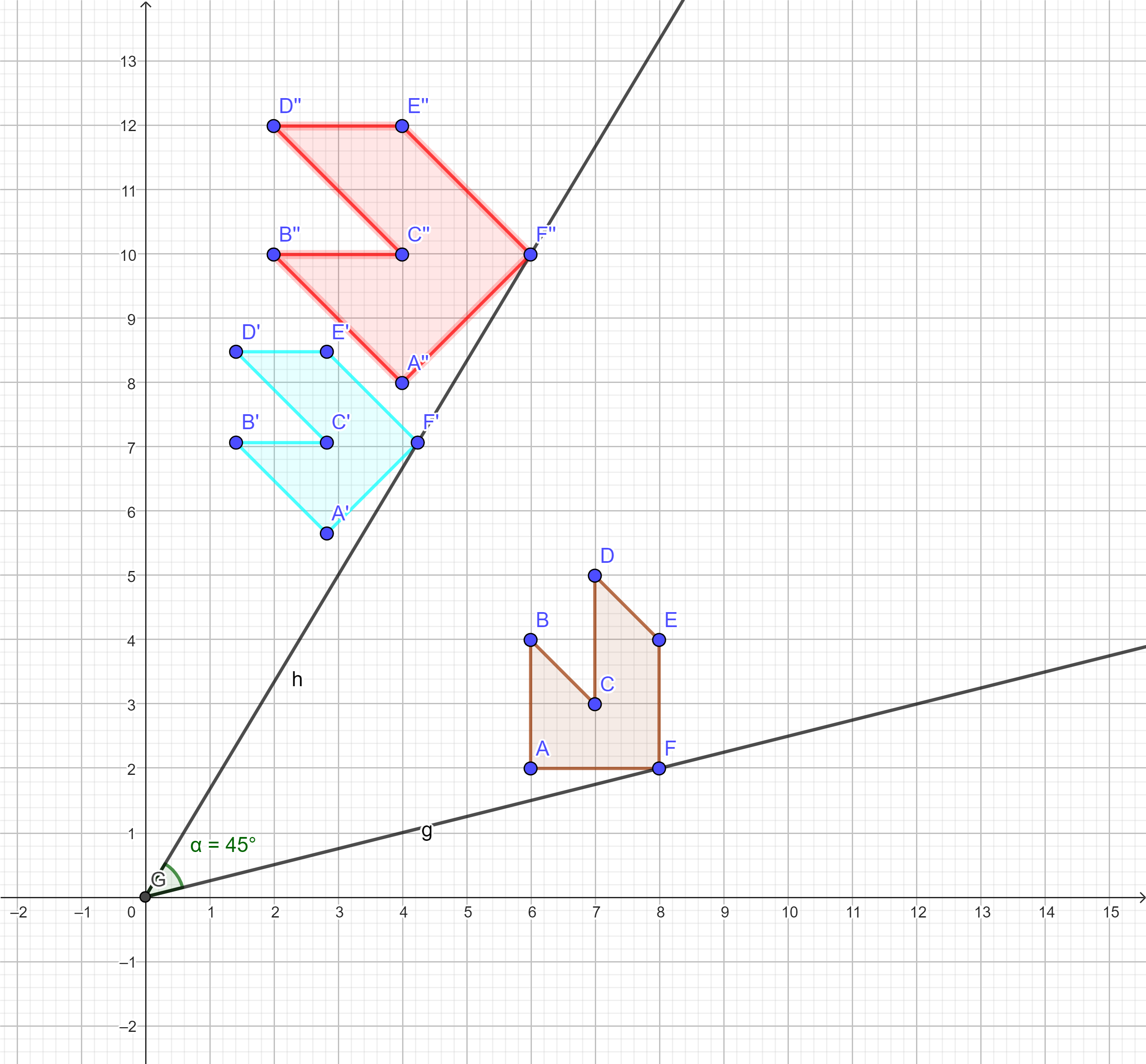
Voici une activité simple sur laquelle j'aimerais votre avis : j'explique très rapidement : je dis aux élèves qu'on prend un point par exemple $A=(6,2)$ et qu'on lui associe le point $A''=(6-2,6+2)$. On aura reconnu la similitude de centre 0, d'angle +45° et de rapport $\sqrt2$. Mes objectifs sont : mesurer des angles (ici $45°$), découvrir une similitude directe (on peut envisager de considérer l'homothétie/agrandissement de centre 0 et de rapport $\sqrt2$, introduire le vocabulaire; ici tout se passe dans le premier quadrant pour fournir une activité faisable dès 10 ans mais on peut envisager de travailler dans les quatre quadrants avec des élèves de 5è où de nouveaux objectifs seront de faire des additions/soustractions de relatifs et éventuellement une initiation au calcul littéral avec les formules $(x,y)\to (x-y,x+y)$.
-
Est-ce un exercice avec des consignes écrites ou bien où l’on suit pas à pas les recommandations du prof ?
-
@Dom : ça dépend : la première fois que je fais faire l'exo, les élèves suivent pas à pas. Quand je réutilise l'exo pour les 5è par exemple, je vais proposer un exercice où il faudra rappeler les règles d'addition ou de soustraction des relatifs par exemple, ou encore s'assurer que l'image d'un angle donné est un angle de même mesure.
-
Honnêtement, sans savoir dans quel cadre précis et quel énoncé et quelles consignes sont données aux élèves, je ne peux pas dire si c’est bien ou non.Ceci a tout à fait sa place en 5e avec comme réserves « quand, comment ».Dans ce fil, j’ai le sentiment que tu es obligé de rappeler souvent les règles de calculs avec les couples.
-
@Dom : je vais reformuler mon questionnement. Si tu veux faire faire de la rotation de $45°$ à des élèves, pas seulement observer sur un dessin déjà fait mais réellement le faire (bref une activité mathématique un peu élaborée, pas juste remplir des exercices à trous), comment tu fais si tu t'interdis par exemple d'utiliser $z'=(1+i)z$? Si la réponse est d'utiliser un rapporteur et de construire patiemment l'image de points avec des angles de $45°$, je répondrais que ça m'étonnerait que ça marche en 2023 avec des élèves lambda. Idem avec un calque.
-
Ça alors. Ce message me semble lunaire.J’ose annoncer que 99,99999% des gens n’utilisent pas (1+i) pour construire des angles de 45° au collège. Le rapporteur est un outil qui fonctionne bien une fois que l’élève est formé.
Bon, pour 45° il y a d’autres choses (diagonale de carré), certes.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres








