Comment déduire le théorème de Pappus d'un cas particulier ?
Bonjour et bonne année
Soit $A, B, C$ trois points sur une droite $f$ et $A', B', C'$ trois points sur une droite $g$. On suppose que $(AB')//(A'B)$ et que $(B'C)//(BC')$. Alors $(A'C)//(AC')$.
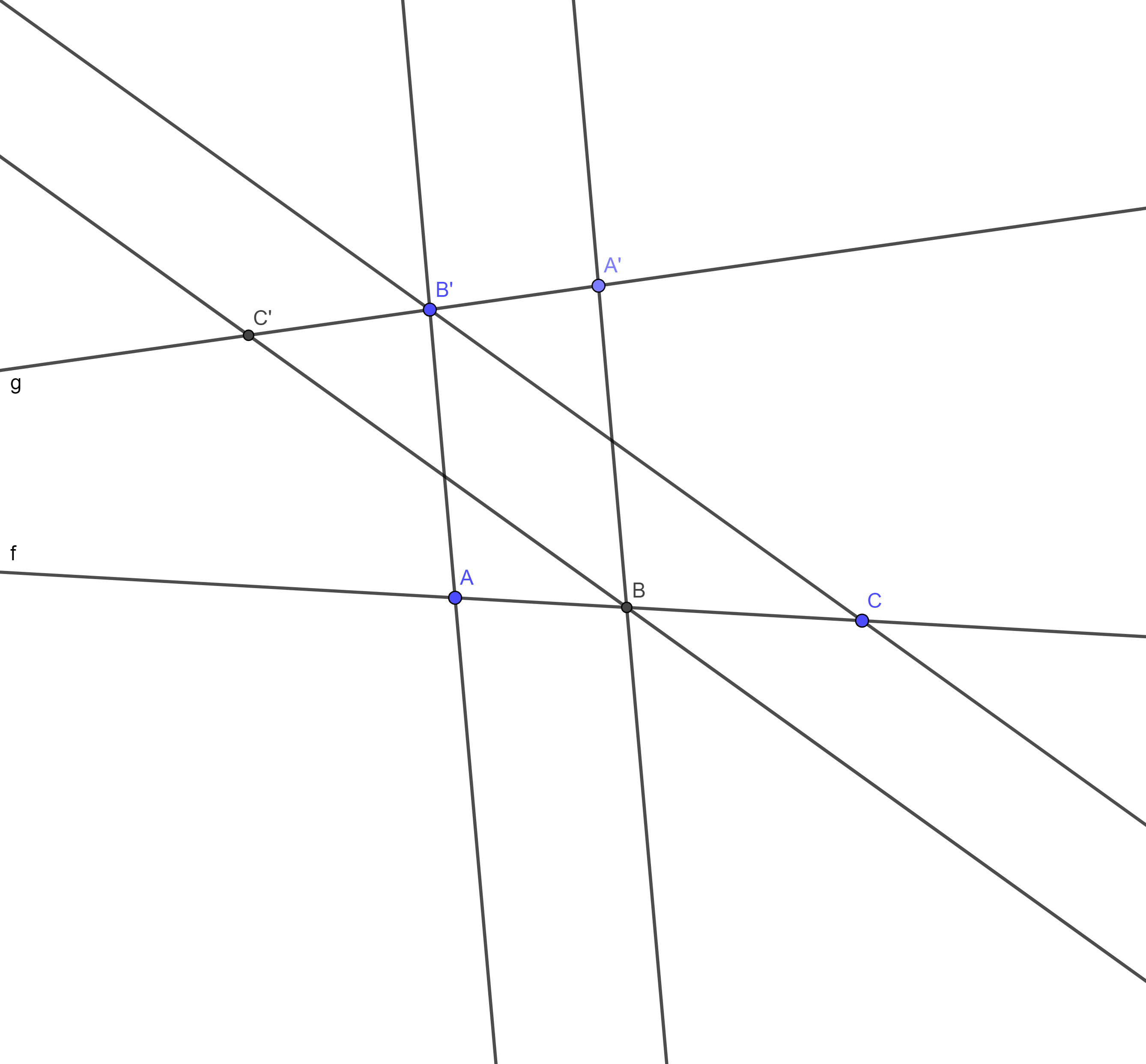
Michèle Audin propose une intéressante démonstration de cette propriété dans le chapitre I de son livre Géométrie. Dans le chapitre 6 consacré à la géométrie projective, après avoir introduit l'espace projectif $P(E)$ associé à un espace vectoriel $E$, elle envisage alors le cas suivant : $(A'B)$ et $(AB')$ sont sécantes en $\alpha$ et $(BC')$ et $(B'C)$ en $\beta$. Et affirme alors que $(A'C)$ et $(AC')$ sont sécantes en $\gamma$ tel que $\gamma\in (\alpha\beta)$. Voici son argument : "On considère la droite projective $\color{red}{(\alpha\beta)}$ comme droite à l'infini... " Le raisonnement suivant paraîtra alors classique sûrement à ceux qui connaissent bien la géométrie projective. Mais tel n'est pas mon cas. Il faut dire que le but louable est ici probablement de donner assez tôt un exemple intéressant pour motiver plus avant l'étude de la géométrie projective et cela au dépens d'arguments mathématiques précis donnés plus tard en exercice.
Mes questions :
1. Qu'est-ce que c'est ici qu'une "droite à l'infini" ? (j'ai compris que si $E=\R^3$, après avoir choisi un plan affine $a+P$ dans $\R^3$, on peut identifier l'espace projectif $P_2(\R)=P(\R^3)$ à $a+P$, auquel on ajoute $\pi(P\setminus\{0\})$, où $\pi: E\setminus\{0\}\to P(E),x\mapsto D_{0x}\setminus\{0\}$ et qu'on appelle $\pi(P\setminus\{0\})$ la "droite à l'infini")
2. Que signifie "la droite projective $(\alpha\beta)$"? (alors que pour moi on est sur un plan affine : $\alpha $ et $\beta$ sont des points non pas d'un espace projectif mais tout simplement d'un plan affine.)
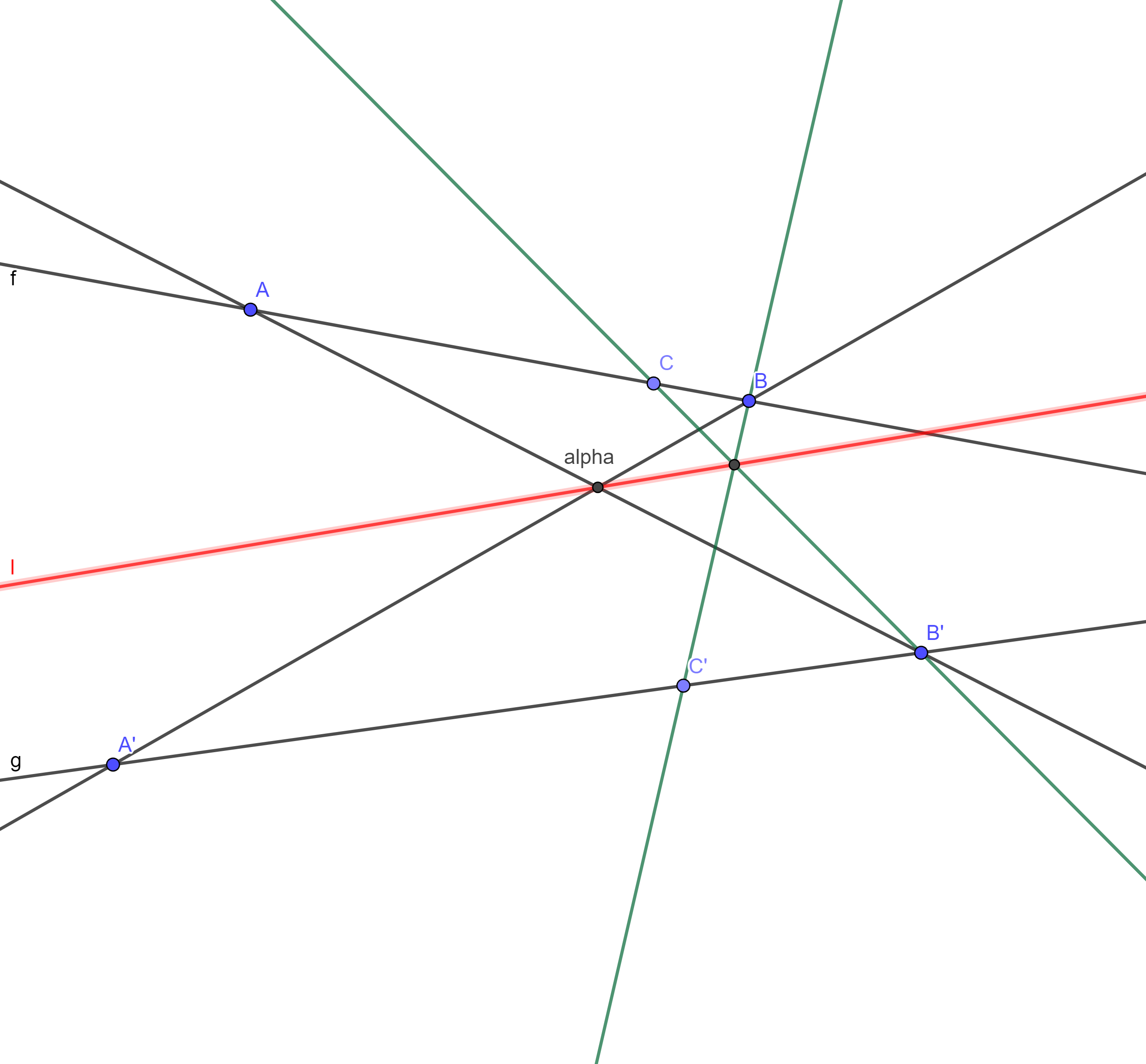
Soit $A, B, C$ trois points sur une droite $f$ et $A', B', C'$ trois points sur une droite $g$. On suppose que $(AB')//(A'B)$ et que $(B'C)//(BC')$. Alors $(A'C)//(AC')$.

Michèle Audin propose une intéressante démonstration de cette propriété dans le chapitre I de son livre Géométrie. Dans le chapitre 6 consacré à la géométrie projective, après avoir introduit l'espace projectif $P(E)$ associé à un espace vectoriel $E$, elle envisage alors le cas suivant : $(A'B)$ et $(AB')$ sont sécantes en $\alpha$ et $(BC')$ et $(B'C)$ en $\beta$. Et affirme alors que $(A'C)$ et $(AC')$ sont sécantes en $\gamma$ tel que $\gamma\in (\alpha\beta)$. Voici son argument : "On considère la droite projective $\color{red}{(\alpha\beta)}$ comme droite à l'infini... " Le raisonnement suivant paraîtra alors classique sûrement à ceux qui connaissent bien la géométrie projective. Mais tel n'est pas mon cas. Il faut dire que le but louable est ici probablement de donner assez tôt un exemple intéressant pour motiver plus avant l'étude de la géométrie projective et cela au dépens d'arguments mathématiques précis donnés plus tard en exercice.
Mes questions :
1. Qu'est-ce que c'est ici qu'une "droite à l'infini" ? (j'ai compris que si $E=\R^3$, après avoir choisi un plan affine $a+P$ dans $\R^3$, on peut identifier l'espace projectif $P_2(\R)=P(\R^3)$ à $a+P$, auquel on ajoute $\pi(P\setminus\{0\})$, où $\pi: E\setminus\{0\}\to P(E),x\mapsto D_{0x}\setminus\{0\}$ et qu'on appelle $\pi(P\setminus\{0\})$ la "droite à l'infini")
2. Que signifie "la droite projective $(\alpha\beta)$"? (alors que pour moi on est sur un plan affine : $\alpha $ et $\beta$ sont des points non pas d'un espace projectif mais tout simplement d'un plan affine.)

Réponses
-
Bonjour,
personnellement, je commencerai à trouver une preuve du cas particulier et ce sans calcul...
puis m'adapter au cas général en restant dans la géométrie élémentaire....puis à voir plus loin...
Sincèrement
Jean-Louis
-
@Jean-Louis Ayme: j'ai évoqué une démo du cas particulier : on suppose $f$ et $g$ sécantes en $0$. Soit $\varphi$ l'homothétie de centre $0$ transformant $A$ en $B$ : elle transforme $B'$ en $A'$ . Soit $\psi$ l'homothétie de centre $0$ transformant $B$ en $C$: elle transforme $C'$ en $B'$. Ces deux homothéties de même centre commutent, autrement dit $\psi\circ \varphi=\varphi\circ\psi$. $\psi\circ \varphi(A)=C$ et $\varphi\circ\psi(C')=A'.$ Donc $(AC')//(A'C).$ Si $f$ et $g$ sont parallèles on utilise des translations.
-
Je viens de visionner avec beaucoup d'intérêt cette vidéo de Cécile Gachet, où des idées intuitives bien utiles sont fournies.
-
Bonsoir,On se place dans un plan projectif dès le départ, et on a deux droites projectives distinctes $f$ et $g$ dans ce plan projectif sur lesquelles on prend des points $A,B, C$ et $A',B',C'$ respectivement.Il reste à démontrer que les points $\alpha,\beta,\gamma$ définis comme tu l'(as écrit sont alignés. Pour cela on envoie la droite $(\alpha,\beta)$ à l'infini, ce qui veut dire qu'on se place dans le plan affine qui est le complémentaire de cette droite dans le plan projectif. On fait alors un raisonnement affine, et on utilise que deux droites affines du plan affine sont parallèles si et seulement si elles se coupent à l'infini.Ça demande un peu de familiarité avec la géométrie projective. Tu as le bouquin de Michèle Audin pour travailler ça, très bien. Un autre document, datant du temps où il y avait de la géométrie projective à l'agreg : https://agreg-maths.univ-rennes1.fr/documentation/docs/Projectif.pdf
-
Bonjour à tous,
en ce qui concerne le cas particulier, le théorème de Reim conduit au résultat....
Sincèrement
Jean-Louis
-
Bonjour, de mémoire, la droite à l'infini dans un plan projectif, c'est la droite sur laquelle vont se couper les droites parallèles du plan affine, complémentaire affine de cette droite projective.Autrement dit, c'est l'ensemble des points à l'infini des droites affines du plan affine, et deux droites parallèles du plan affine ont le même point à l'infini, correspondant à la direction des droites.En effet, dans le plan projectif, deux droites projectives se coupent en un unique point, et quand les deux droites sont affines et parallèles (plus exactement en prenant la partie affine d'une droite projective, celle située dans le plan affine), comme elles ne se coupent pas dans le plan affine, elles se coupent forcément sur la droite projective à l'infini.Après, la construction algébrique est plus complexe.Rappel : de manière générale $\mathbb P(E)= ( \mathbb P(E) \setminus \mathbb P(F)) \cup \mathbb P(F)$ (évidemment), où $E$ est un espace vectoriel de dimension $n+1$, $\mathbb P(E)$ est l'ensemble des droites vectorielles de $E$, espace projectif associé de dimension $n$ (par convention), $F$ un hyperplan vectoriel de $E$, $\mathbb P(F)$ son espace projectif associé (hyperplan projectif), et $ \mathbb P(E) \setminus \mathbb P(F)$ a une structure affine de direction $F$.Pour $n+1=3$, ceci peut se représenter à l'aide d'un dessin en prenant deux plans parallèles disjoints $F$ (plan vectoriel) et $Q$ (plan affine) et la projection centrale de centre $O \in F$ sur $Q$ : on a une bijection entre l'ensemble des droites vectorielles de l'espace de dimension $3$ non contenues dans $F$, autrement dit $\mathbb P(E) \setminus \mathbb P(F)$, et $Q$ plan affine. Il reste alors les droites vectorielles contenues dans $F$, autrement dit $\mathbb P(F)$, dans un ensemble disjoint.Avec $n=2$, on a $\mathbb P(E) =$ plan affine $\cup$ droite projective à l'infini. On peut prendre n'importe quelle droite projective du plan projectif comme droite à l'infini.L'avantage de se placer dans un plan projectif (par rapport à un plan affine), c'est qu'on n'est plus obligé de faire des cas particuliers dans les démonstrations selon que les droites sont parallèles ou sécantes (car deux droites se coupent en un unique point), et qui peut le plus peut le moins, à savoir tout ce qui est valable dans le plan projectif est valable dans le plan affine complémentaire une fois choisie la droite à l'infini (sachant que cette droite a elle-même un point à l'infini, mais cela n'a pas d'importance dans les démonstrations).
-
la droite à l'infini (sachant que cette droite a elle-même un point à l'infini ...
Bizarre. Tu veux en fait dire que la droite à l'infini est une droite projective ?
-
C'est ça, je l'ai dit plus haut.
-
Bonsoir,
http://jl.ayme.pagesperso-orange.fr/vol6.html
puis
Une rêverie de Pappus d'Alexandrie p.. 3-6 , 10-15.
Sincèrement
Jean-Louis
-
Merci à tous. Il y a aussi cet article de la série Images des mathématiques du cnrs, où Christine Huyghe envoie une droite rouge à l'infini. Toujours des idées intuitives intéressantes mais je ne serai probablement satisfait que si j'arrive à transformer toutes ces belles évocations en calculs rigoureux. Je trouve très intéressant l'essai de Claire Voisin ici pour introduire la géométrie projective à des lycéens sans faire la moindre concession à la rigueur mathématique. J'aime bien la notation $\mathbb RP^1$ par exemple pour désigner la droite projective de $\mathbb R^2$ (et de façon générale $\mathbb RP^n$ pour l'espace projectif de $\mathbb R^{n+1}$) et la représentation de $\mathbb RP^1$ proposée par Christine Huyghe comme un cercle. @GaBuZoMeu, je suis ton conseil de poursuivre mon étude de Géométrie. À propos des homographies de la droite projective (p. 194), on y lit " le point à l'infini $\infty=(1,0)$". Voilà une écriture enfin concrète de ce fuligineux "point à l'infini" qui peut peut-être suffire à des artistes peintres mais certainement pas à des matheux
 . Un peu plus loin, le birapport de quatre points $a, b, c, d$ d'une droite affine est donné par $$[a,b,c,d]=\frac{d-b}{d-a}/\frac{c-b}{c-a}$$
. Un peu plus loin, le birapport de quatre points $a, b, c, d$ d'une droite affine est donné par $$[a,b,c,d]=\frac{d-b}{d-a}/\frac{c-b}{c-a}$$
-
Je poursuis ma réflexion : envoyer une droite à l'infini, c'est "choisir une transformation affine qui transforme la droite en la droite à l'infini . Et cela est facile parce que le groupe des transformations affines est gros." ( Claire Voisin dans le document indiqué plus haut à 1:00:00) C'est ce qui est confirmé dans Géométrie p. 195 : " c'est une homographie qui envoie la droite en pointillés sur la droite à l'infini" avec deux exercices proposés (ex VI.14 et ex VI.15) qui devraient enfin achever de répondre à mes questions. Sinon, j'ai trouvé ce petit bijou avec Thalès, Menelaüs, Pascal et son hexagramme mystique.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres





