Conjectures arithmétiques

stfj

Bonjour. 
J'ai étudié avec beaucoup d'intérêt et pendant assez longtemps des listes de nombres premiers consécutifs prises au hasard telles que :  

35689747	35689757	35689769	35689777	35689789	35689799	35689831	35689837	35689853	35689891
35689937	35689939	35689943	35689949	35689963	35690003	35690009	35690023	35690027	35690047
35690077	35690087	35690093	35690101	35690107	35690111	35690141	35690143	35690153	35690167
35690177	35690201	35690231	35690233	35690243	35690251	35690287	35690309	35690321	35690323
35690353	35690363	35690371	35690381	35690399	35690401	35690407	35690423	35690453	35690467

 Ce qui m'intéresse d'abord dans ces listes, c'est par exemple les triplets tels que $(35\,689\,747,35\,689\,757,35\,689\,789)$. On remarque qu'il s'agit d'un triplet de la forme $(p,p+10,p+42)$, où $p+10$ et $p+42$ ne sont pas consécutifs. Le fait que les nombres premiers soient consécutifs ou pas ne m'importe pas du tout. Même pour des doublets que je me propose d'étudier ci-dessous.
Il y a dans cette toute petite liste deux nombres $p$ tels que $p+10$ est aussi premier, à savoir $35689747$ et $35689789$; ainsi que deux nombres $p$ tels que $p+30$ est aussi premier, à savoir $35689747$ et $35689769$. Il n'y a aucun jumeau($p+2$), aucun sexy($p+6$), aucun cousin($p+4$), quelques champions sauteurs de Conway($p+2310$), mais évidemment la liste est si petite qu'on en retirerait que peu d'information. Aussi je me suis peu à peu trouvé équipé d'outils informatiques me permettant d'étudier d'assez longues listes de $p$.
Par ailleurs, je m'étais intéressé à la suite de $\mathbb{Z}$-algèbres $(\mathbb{Z}/2\mathbb{Z}, \mathbb{Z}/6\mathbb{Z}, \mathbb{Z}/30\mathbb{Z}, \mathbb{Z}/210\mathbb{Z},...)$ définie à partir des primorielles $(2,2\times3,2\times3\times5,2\times3\times5\times7,...)$ où à propos d'objets associés à des doublets apparaît naturellement la suite $(c_n)_n:=(2, \frac83,\frac{16}{5},..., c_n\times \frac{p-1}{p-2},...)$, qui apparaît dans les conjectures de Hardy-Littlewood.
Tout cela, je l'ai mené assez naïvement à la suite de la lecture de Merveilleux nombres premiers de Jean-Paul Delahaye qui rapporte en particulier les travaux récents de la fin des années 1990 de Wolf, Odlyzko et Rubinstein sur les champions sauteurs de Conway, qui les baptisa ainsi en 1997 je crois. 
Ce qui m'interpelle est que M.Wolf, en exigeant le caractère consécutif, "a conjecturé et vérifié par des sondages" que les champions sauteurs apparaissent respectivement pour $389, 1.7\times10^{36}, 5.81\times10^{428}, 1.48\times10^{8656}, ...$, alors qu'il me semble que j'obtiens plus de résultats(par exemple les rapports $2, \frac83,....)$ simplement sur de petites listes. 
Ce que je propose ici est de vous montrer le peu que je connais du sujet, de me soumettre à votre regard critique constructif pour comprendre ce qui éventuellement n'irait pas. Par ailleurs, je dispose d'un programme avec lequel nous pourrions explorer quelques listes et étudier des doublets($p+2,p+4,p+6,p+8,p+10,p+30,p+210,p+2310$) si le coeur vous en dit.
Cordialement.

stfj

erreur : 5 jumeaux, 3 cousins, 7 sexys, 11 $p+10$, 10 $p+30$, 15 $p+210$, 14 $p+2310$ :

stfj

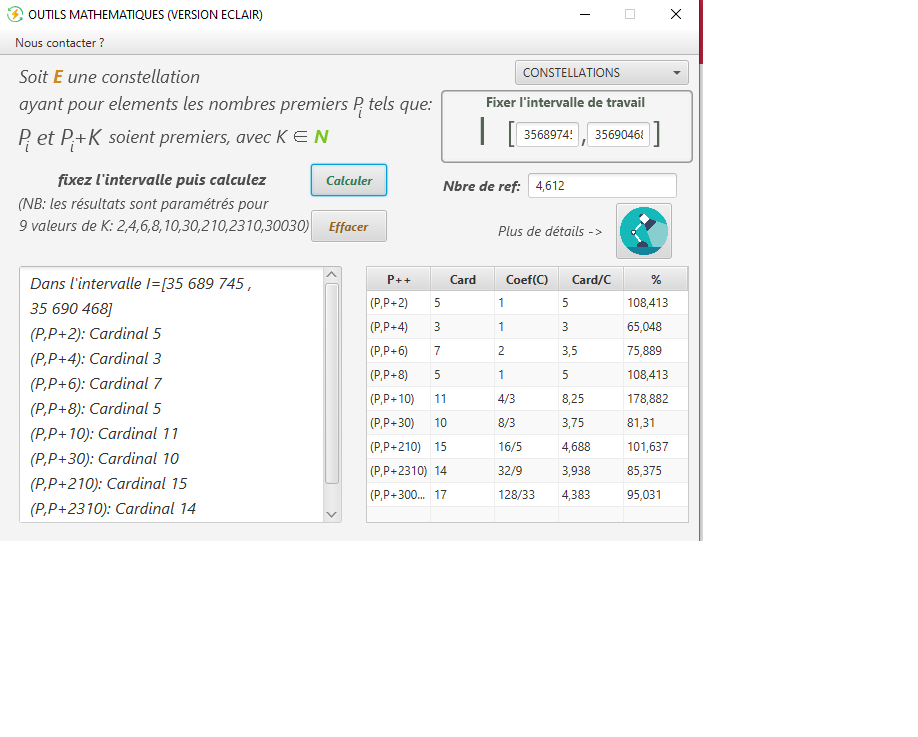
Quand on prend une liste suffisamment longue, par exemple $[\![35\,689\,747;50\,000\,000]\!]$, on obtient des résultats très proches de ceux que l'on peut conjecturer, ce que traduisent les pourcentages affichés ci-après : 

stfj

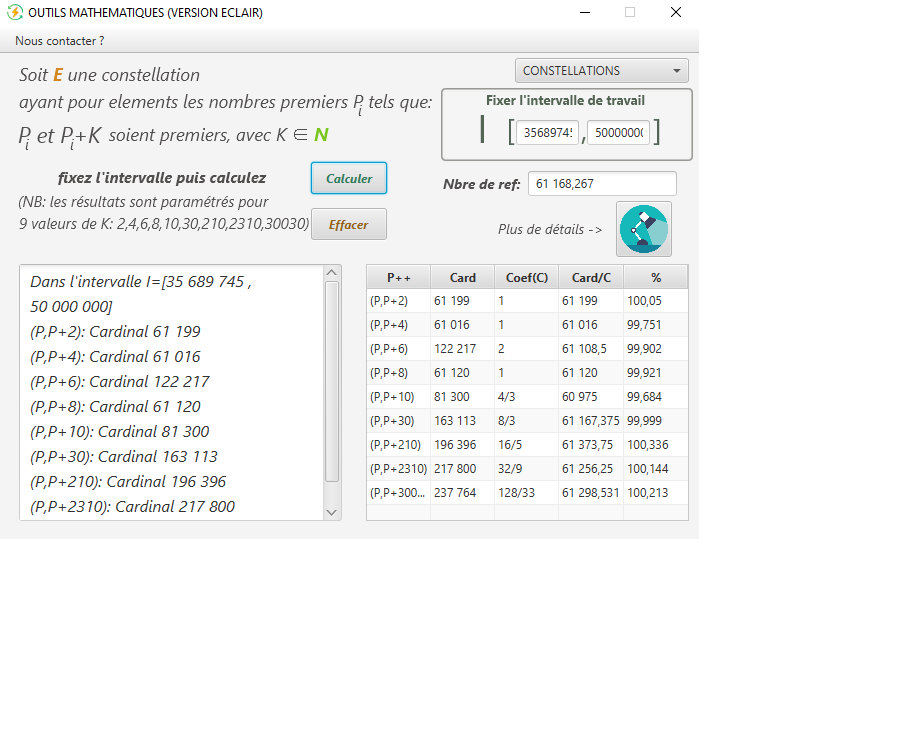
De façon provocatrice, John Conway s'est-il trompé de définition en définissant les "jumping champions"(champions sauteurs) ? 

Al-Kashi

Il est temps que tu arrêtes ton monologue stfj