Points d'un plan affine et vecteurs d'un plan vectoriel

Lol_a

Bonjour,
à la lecture d'un autre sujet où quelqu'un a parlé de points d'un plan affine et de vecteurs d'un plan vectoriel je me rends compte que je ne suis pas totalement au clair avec ces notions. En fait, je n'ai aucun souci avec la géométrie niveau lycée, j'ai étudié les espaces vectoriels et par exemple pour moi un espace vectoriel de dimension 1 est une droite qui passe par l'origine et un plan affine est e.v. de dimension 2 qu'on aurait mais j'ai pas beaucoup de recul sur ces notions et en particulier je ne saurais pas bien décrire ce qui les unit et je ne sais jamais quand/s'il faut mettre des flèches sur les vecteurs. Pour moi un points ou un vecteur (mais du coup ça revient presque au même) c'est surtout un n-uplet de nombres appelés coordonnées.

Bref, ce sont des choses que j'ai vues par-ci par-là et qui du coup sont un peu en désordre (manque de rigueur) dans ma tête. Pourriez-vous, s'il vous plait, m'aider à y voir plus clair ? Quel est "le" "schéma de construction" de ces notions ?

Riemann_lapins_cretins

L'idée de la géométrie affine c'est de répondre à cette question, en un sens : l'objet $y = 3x + 4$ est de quelle nature ?

Si on pose cette question dans une classe de sup et que les élèves répondent "c'est une droite" ils ont faux : leur a-t-on parlé de droite ne passant pas par 0 ?
Mais ça reste bien une droite, tant pour notre satisfaction personnelle que d'après le cours du collège (lycée maintenant ?).

L'idée de la géométrie affine c'est de donner le droit de décaler un espace vectoriel.
Le rôle du "point" est de permettre ce décalage, de pouvoir considérer un espace vectoriel ayant une origine qu'on choisit nous-même.

Pour un vrai "schéma de construction" je ne vois pas quoi suggérer d'autre que de prendre un cours de géométrie affine qui donne les axiomes de base.
La construction se fait en se donnant un espace vectoriel et un ensemble quelconque (les points), une "soustraction" qui transforme deux points en vecteur et une addition entre vecteurs et points qui donne des points, avec les axiomes qu'il faut pour que les opérations soient "bien compatibles" entre elles et avec la structure vectorielle sous-jacente.

Plus important, une application affine est simplement une application de l'ensemble des points dans lui-même qui s'écrit sous la forme : $f(P) = f(M) + df(P-M)$ avec $df$ linéaire.
C'est je pense la notion importante et celle qui m'a fait comprendre l'idée simple "point + espace vectoriel".

Étant donné que toute la théorie vectorielle est faite, ces axiomes permettent de récupérer rapidement des faits connus du lycée sans preuve.
Ils permettent surtout d'utiliser la puissance de l'algébrisation de la géométrie qui dans le cadre purement vectoriel nous bloque vite (car encore une fois il y a un point privilégié : la géométrie affine permet de donner au point qu'on veut l'importance du 0 et d'utiliser ensuite l'algèbre linéaire qu'on connaît déjà).

pappus

Bonjour à tous

Grosso modo, la géométrie (affine, euclidienne, projective, etc ,...) ne s'use que si l'on s'en sert!

Amicalement

pappus

stfj

@Riemann_lapins_cretins : bonjour. Je trouve quand même surprenant que "dans une classe de sup [si] les élèves répondent "c'est une droite" ils ont faux : leur a-t-on parlé de droite ne passant pas par 0 ?". Soit $E$ un espace vectoriel réel . Qu'est-ce qui interdit dès l'introduction de cette notion d'appeler droite vectorielle un ensemble de la forme $\mathbb{R}.u$, où $u$ désigne un élément non nul de $E$? Et droite affine un ensemble de la forme $b+\mathbb{R}.u$, où $b$ désigne un point de $E$ et $u$ un vecteur non nul de $E$?
 @Lol_a : bonjour.  Cela fait longtemps qu'en mathématiques, plus grand monde n'utilise de flèche : on écrit simplement vecteur $u$ au lieu de la notation lourde $\vec{u}$. En gros, ton point de vue (nulle différence sauf d'interprétation concrète des objets mathématiques que l'on manipule) à faire entre un point et un vecteur: ce sont tout simplement des éléments d'un espace vectoriel) est celui que je partage. 
Mais, si je m'arrête là, je subirai sans doute les foudres de @pappus. Existe par exemple la notion d'espace affine sur laquelle il est malheureusement pour un enseignant difficile de faire l'impasse. Michèle Audin a écrit Géométrie et son livre commence par un chapitre où elle introduit cette notion avant d'aborder par la suite aussi rapidement que possible les joyeusetés que nous propose par ci par là @pappus par exemple, et sur lesquelles je ne suis pas compétent pour parler davantage. Mais ce sont évidemment des mathématiques sans lesquelles prétendre faire des mathématiques est illusoire.

Lol_a

Merci @Riemann_lapins_cretins pour ces pistes. En fait, j'avais bien compris l'idée de "espace affine = espace vectoriel + 1 point" (qu'on utilise aussi pour résoudre certaines équations différentielles) mais j'aurais beaucoup de mal à l'écrire proprement dans un cours pour des élèves du supérieur par exemple. Je vais essayer de construire en partant des axiomes que tu as donné.

stfj

Deux points de vue (A et B ): 
A)
A.1. - Disposer de la notion d'espace affine $(\mathcal{E},(E,+,.),\phi)$;
A.2. - Grâce aux propriétés de $\phi$ que l'on a par définition, choisir un point arbitraire(c'est ce choix arbitraire qui fait tout l'intérêt de la notion d'espace affine) et établir alors une bijection entre $E$ et $\mathcal{E}$
On est alors ramené à un outil raisonnable, la notion d'espace affine faisant figure d'épouvantail pour la plupart des mathématiciens.
B ) 
B.1. - Disposer de la notion d'espace affine;
B.2. - Soit E un espace vectoriel. S'assurer que $(E,E,\phi)$ est un espace affine, où l'on a posé $\phi(a,b):=b-a$.
J'ai pas raconté trop de bêtises, cette fois, @pappus, ?

lourrran

J'ai l'impression que cette discussion pourrait opposer la génération des moins de 45 ans et celle des plus de 45 ans. A voir si la frontière est à 45 ans, ou 50 ???

Si on s'intéresse aux droites vectorielles (sans aucune allusion du genre s.e.v d'un e.v de dimension supérieure), alors il y a une et une seule droite vectorielle.
Si on voit ça comme un s.e.v d'un e.v. de dimension supérieure, alors une droite vectorielle est une direction. Je n'aime pas du tout la référence au point Origine.

Extrait : L'idée de la géométrie affine c'est de donner le droit de décaler un espace vectoriel.
Pour moi, la géométrie affine (la géométrie de Pappus) vient en premier. 

Définir la géométrie affine à partir de la géométrie vectorielle, ça me pique les yeux.
En géométrie affine, on a des cercles, des paraboles etc etc. Des choses qu'on ne peut pas du tout relier à la géométrie vectorielle.

pldx1

Bonjour
Selon les objectifs, on s'équipe différemment.

Si l'on veut démontrer le théorème fondamental de la géométrie projective, il faut tout un arsenal. Et alors, au bout d'un semestre, on arrive à: "tout espace affine est un sous-truc d'un espace vectoriel". Et on est content. On a tué un semestre.

L'autre méthode, c'est d'utiliser $b=a+(b-a)$. Et alors, dès le lendemain, on peut faire des mathématiques.

Par exemple "l'objet  $y=3x+4$ est de quelle nature" ?  Réponse attendue de la part d'un montagnard : "de quelle nature est la nature naturante sous-tendant une telle question" ?  On pourait tout autant demander: "de quoi sont les pieds"? Et la réponse attendue serait "une sentinelle ne doit s'assoir sous aucun prétexte".

Si l'on veut faire des mathématiques,  on sépare les torchons et les serviettes. Cela donne $M \doteq x:y:1 \;;\;   \Delta \doteq  [3,-1,4]$ suivi de $$M \in \Delta \Longleftrightarrow \Delta \cdot M =0$$ 

Cordialement, Pierre.

JLapin

@Lol_a
Deux réponses possibles à ta demande d'axiomatisation.

Une réponse très partielle mais suffisante pour décrire l'ensemble solution d'une équation linéaire avec second membre (par exemple, une équa diff linéaire) consiste à définir la notion de sous-espace affine d'un espace vectoriel. Ton sous-espace affine, pourra alors être qualifié de droite affine, plan affine, hyperplan affine, etc.

Une réponse plus complète consiste à définir la notion d'espace affine.
https://fr.wikipedia.org/wiki/Espace_affine
puis celle de sous-espace affine d'un espace affine.

La première réponse est un cas particulier de la seconde (celui où l'espace affine est aussi l'espace vectoriel qui apparait dans la définition générale d'un espace affine).

Si tu prépares un concours sur un programme particulier, regarde-le pour savoir si tu dois en priorité maîtriser l'une ou l'autre des situations.

Julia Paule

Pour compléter ce que dit JLapin, pour définir la notion d'espace affine dans la réponse plus complète, il faut avoir vu préalablement la notion d'action d'un groupe (l'espace vectoriel) sur un ensemble (de points).
Je me suis longtemps posée cette question de savoir pourquoi on commençait par définir la notion de sous-espace affine d'un espace vectoriel, avant celle d'espace affine directement.

JLapin

Je pense que c'est à cause des équations linéaires avec second membre en fait (sans parler du fait qu'en dimension finie, par le choix d'un repère, on se ramène finalement à $K^n$).

Julia Paule

Oui, mais c'est piégeur : on commence par parler de sous-espace affine, du coup on se demande ce que peut bien être un espace affine. Question de vocabulaire.
En fait, point = vecteur dès qu'on a placé une origine, et pour définir un sous-espace affine, on l'utilise dans l'autre sens = vecteur + espace vectoriel, c'est un peu tordu a priori.

Lol_a

Merci pour toutes vos réponses qui sont toutes très intéressantes.
@stfj Merci pour ta réponse sur les flèches. Je mets le livre dont tu parles sur ma liste d'ouvrages à feuilleter
@lourran C'est vrai que je me suis beaucoup appuyée sur mes connaissances de géométrie affine du lycée pour comprendre les espaces vectoriels.
@JLapin Je posais la question plus pour ma culture personnelle et ma pratique d'enseignante mais comme je préparer l'agreg interne c'est effectivement une bonne idée de consulter le programme. Je cite "Définition d’un espace affine réel. Espace vectoriel associé. [...]"
@Julia Paule Je n'avais pas pensé aux actions de groupes, merci !

GaBuZoMeu

Bonjour,

Une question embarrassante : l'ensemble des solutions du système

$$\left\{ \begin{align} x+y+z&=1\\x+2y+3z&=2\\y+2z&=0\end{align}\right.$$

est-il un sous-espace affine (et donc un espace affine) ?

JLapin

J'aurais dit non mais apparemment, ce n'est pas unanime.

https://www.bibmath.net/dico/index.php?action=affiche&quoi=./a/affine_espace.html

GaBuZoMeu

Suivant la définition de bibmath que je cite.

On dit qu'un ensemble $\mathcal E$ est un espace affine s'il existe un espace vectoriel $E$ et une application de $\mathcal E×E$ dans $\mathcal E$ qui au point $A$ et au vecteur $\overrightarrow u$ associe un point de $\mathcal E$ noté $A+\overrightarrow u$ vérifiant

$$\forall A\in \mathcal E,\ \forall \overrightarrow u,\overrightarrow v \in E,\quad (A+\overrightarrow u)+ \overrightarrow v=A+(\overrightarrow u + \overrightarrow v)$$

$$\forall (A,B)\in \mathcal E^2,\ \exists! u \in E,\quad A+\overrightarrow u=B\;.$$

L'ensemble des solutions du système ci-dessus est bien un espace affine.

JLapin

Et d'après cette définition, non

https://membres-ljk.imag.fr/Bernard.Ycart/mel/ga/node5.html

stfj

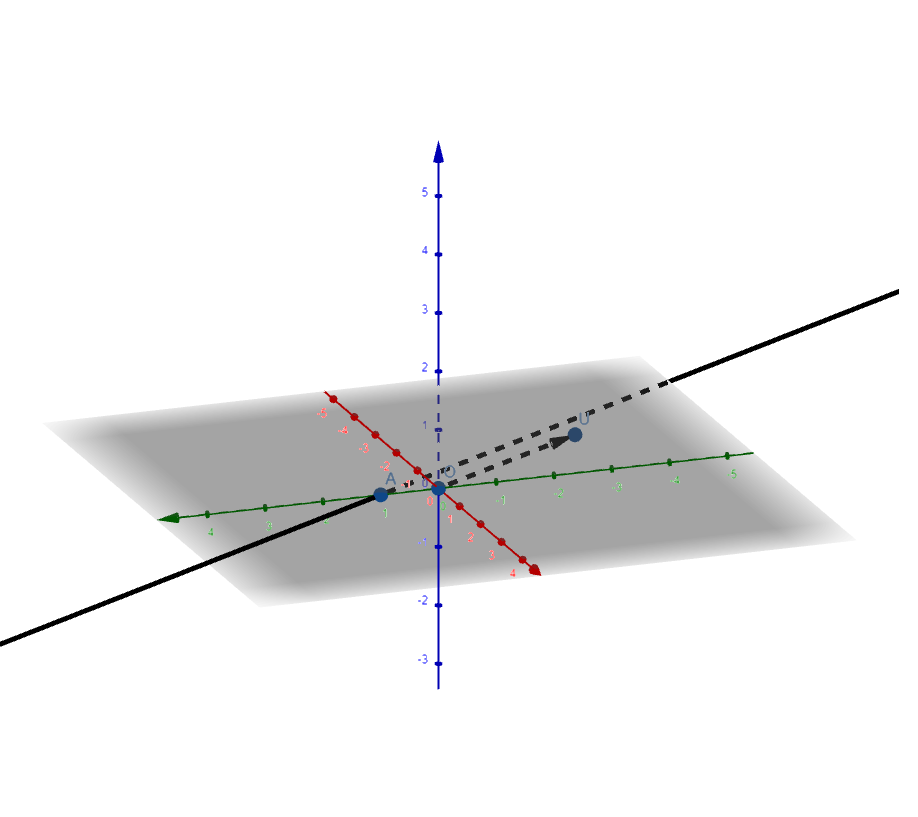
@GaBuZoMeu : bonjour. Ton exemple est mal choisi. Le système que tu proposes n'a pas de solution. Prenons $\begin{cases} x+y+z=1\\ x+2y+3z=2 \end{cases}$. Ce système se réduit à $\begin{cases} x=0+1z\\ y=1-2z \\z=0+1z \end{cases}$. L'ensemble des solutions du système est donc la droite affine de $\mathbb{R}^3$ passant par le point $A=(0,1,0)$ et dont $u=(1,-2,1)$ est un vecteur directeur. Autrement dit plus simplement, l'ensemble des solutions est $(0,1,0)+\mathbb{R}.(1,-2,1)$. Par exemple, on peut vérifier que $(0,1,0)+(1,-2,1)$ est solution; ainsi que $(0,1,0)+2.(1,-2,1)$. Le dessin n'apporte pas grand chose mais une droite reste une droite si j'ose dire, que ce soit Gauss qui envisage le système ou en 2022.

Riemann_lapins_cretins

Peut-être que l'exemple est choisi comme de par un fait exprès.

GaBuZoMeu

stfj, je suis surpris que tu n'aies pas compris que j'ai choisi mon exemple justement parce que le système n'a pas de solution. Pourquoi aurais-je dit sinon que la question est embarrassante ?