La "catégorie" Z/2 ?
Bonjour à toutes et à tous et merci pour l'accueil récent sur Les-Mathématiques.net
Je m'intéresse depuis peu aux catégories et on m'excusera ma question sans doute "bête":
La catégorie des ensembles préordonnés Poset m'a interpelé. Je me demandais si définir la catégorie suivante, notons-la F'2, pose problème :
* Les objets de F'2 sont les entiers relatifs, ie les éléments de $ Z = \{ \text{... ,} -3,-2,-1,0,1,2,3,4,\text{...} \}$. (remarque: F'2 sera donc une petite catégorie au sens où ses objets forment un ensemble, en l'occurence $Z$);
* Les flèches de F'2 sont inspirées de celles de Poset. Soit $m$ et $n$ deux objets. $Hom(m,n)=\begin{cases} \{ \varnothing \}, & \text{si }m-n \in 2 \Z \\ \varnothing, & \text{si }m-n\in 1+2\Z \end{cases}$
Pour l'instant, j'ai fait des dessins avec les pairs en bleu et les impairs en rouge ; et dessiné quelques flèches ; je n'ai pas vérifié un à un les axiomes mais cela me paraît essentiellement trivial. Si la définition de F'2 en tant que catégorie est correcte, elle est certainement définie quelque part dans un cadre probablement plus général. En l'occurrence, est-ce que F'2 apporte quelque chose de plus par rapport à $\Z / 2\Z$ ? Est-ce que c'est utilisé quelque part ? Je songe à l'intérêt de présenter l'ensemble $\Z / 2\Z$ sans sa structure d'anneau de cette façon "colorée" à des personnes qui découvrent les entiers modulo 2... D'un point de vue personnel, il y a une phrase qui me revient :"le lecteur sera vite amené à ajouter de lui-même beaucoup d'autres exemples en réfléchissant à la structure de ses connaissances" (Introduction aux catégories et aux problèmes universels, Jaffard-Poitou, 1971). J'avais envie de partager cet exemple (peut-être faux ou non pertinent) avec vous.
Cordialement.
Je m'intéresse depuis peu aux catégories et on m'excusera ma question sans doute "bête":
La catégorie des ensembles préordonnés Poset m'a interpelé. Je me demandais si définir la catégorie suivante, notons-la F'2, pose problème :
* Les objets de F'2 sont les entiers relatifs, ie les éléments de $ Z = \{ \text{... ,} -3,-2,-1,0,1,2,3,4,\text{...} \}$. (remarque: F'2 sera donc une petite catégorie au sens où ses objets forment un ensemble, en l'occurence $Z$);
* Les flèches de F'2 sont inspirées de celles de Poset. Soit $m$ et $n$ deux objets. $Hom(m,n)=\begin{cases} \{ \varnothing \}, & \text{si }m-n \in 2 \Z \\ \varnothing, & \text{si }m-n\in 1+2\Z \end{cases}$
Pour l'instant, j'ai fait des dessins avec les pairs en bleu et les impairs en rouge ; et dessiné quelques flèches ; je n'ai pas vérifié un à un les axiomes mais cela me paraît essentiellement trivial. Si la définition de F'2 en tant que catégorie est correcte, elle est certainement définie quelque part dans un cadre probablement plus général. En l'occurrence, est-ce que F'2 apporte quelque chose de plus par rapport à $\Z / 2\Z$ ? Est-ce que c'est utilisé quelque part ? Je songe à l'intérêt de présenter l'ensemble $\Z / 2\Z$ sans sa structure d'anneau de cette façon "colorée" à des personnes qui découvrent les entiers modulo 2... D'un point de vue personnel, il y a une phrase qui me revient :"le lecteur sera vite amené à ajouter de lui-même beaucoup d'autres exemples en réfléchissant à la structure de ses connaissances" (Introduction aux catégories et aux problèmes universels, Jaffard-Poitou, 1971). J'avais envie de partager cet exemple (peut-être faux ou non pertinent) avec vous.
Cordialement.
Réponses
-
Je ne sais pas si j'ai bien compris ta définition mais les classes $Hom()$ ne peuvent pas avoir de flèches en commun. Or dans ta définition il n'y a qu'une seule flèche (ou morphisme) en tout et pour tout. De plus il te faut définir la composition des flèches.
Par contre je ne présenterais pas $\Z / 2\Z$ ainsi. Les morphismes (qui sont des "flèches", donc orientées) n'ont rien à voir avec $\Z / 2\Z$. -
bonjour @raoul.S
Prenons par exemple les objets 4 et 6 et 8. Hom(4,6)=$\{ \varnothing \}$ et Hom(6,8)=$\{ \varnothing \}$ . [remarque: $\{ \varnothing \}$ est une autre façon de noter "1 flèche de 4 à 6" et $\varnothing$, 0 flèche de 7 à 8 par exemple]. La composée de la flèche de 4 à 6 avec la flèche de 6 à 8 est la flèche de 4 à 8.
Un dessin sera plus parlant :
-
Oui je me disais que c'est ça que tu voulais dire mais ce n'est pas ça que tu dis en fait. Car en disant que $Hom(4,6)=\{\emptyset\}=Hom(6,8)$ tu dis que la flèche qui relie 4 à 6 est la même que celle qui relie 6 à 8 (cette flèche étant $\emptyset$), or ça ce n'est pas possible dans une catégorie.
Bref pour traduire ton idée il faudrait dire que pour tout nombres entiers $n,m$ ayant même parité, $Hom(n,m):=\{(n,m)\}$. Donc l'unique flèche reliant 4 à 6 est notée $(4,6)$ et l'unique flèche reliant 6 à 8 est notée $(6,8)$.
À partir de là la composition des flèches est facile à définir, on pose $(n,m)\circ (m, k):=(n,k)$. Ainsi $(4,6)\circ (6,8)$ est bien égal à $(4,8)$...
-
@raoul.S : ok. J'avais trouvé ça sur un autre post à propos de la catégorie des ensembles préordonnés et avais trouvé ça marrant avec $\{ \varnothing \}$ et $\varnothing$ . Mais c'est vrai que c'est ambigu. On peut peut-être préciser l'idée en indiquant la source de la flèche et son but : ça donnerait : $$Hom(m,n)=\begin{cases} (m,n,\{ \varnothing \}), & \text{si }m-n \in 2 \Z \\ \varnothing, & \text{si }m-n\in 1+2\Z \end{cases}$$Chais pas. De toute façon, j'en retiens que mieux vaut en rester au flou "$1$ flèche si ..., $0$ flèche si..." si cela ne pose pas de problème de compréhension, ou préciser comme tu le fais si besoin est.
Merci. -
D'ailleurs j'aurais dû écrire $Hom(n,n):=\{(n,m)\}$ au lieu de $Hom(n,n):=(n,m)$ dans mon dernier post. J'ai corrigé.
Je préfère ça : $Hom(m,n):=\begin{cases} (m,n), & \text{si }m-n \in 2 \Z \\ \varnothing, & \text{si }m-n\in 1+2\Z \end{cases}$
car à moins que quelque chose m'échappe, le $\varnothing$ est superflu dans le triplet. -
raoul.S : plus simplement,\[\text{Hom}(m,n):=\begin{cases} \{(m,n)\}, & \text{si }m-n \in 2 \Z \\ \varnothing, & \text{sinon.} \end{cases}\]Il me semble que cette façon de procéder existe déjà.
Le chat ouvrit les yeux, le soleil y entra. Le chat ferma les yeux, le soleil y resta. Voilà pourquoi le soir, quand le chat se réveille, j'aperçois dans le noir deux morceaux de soleil. (Maurice Carême). -
Oui c'est mieux. D'ailleurs j'ai encore oublié les accolades...
-
@raoul.S : comme l'on travaille dans $\Z$ et aucunement dans $\N$, je me demande s'il ne faudrait pas écrire ceci :\[\text{Hom}(m,n):=\begin{cases} \{(m,n),\,(n,m)\}, & \text{si }m-n \in 2 \Z \\ \varnothing, & \text{sinon.} \end{cases}\]toutes les fois que $m$ et $n$ sont dans $\mathscr{C}_0=\Z$.Le chat ouvrit les yeux, le soleil y entra. Le chat ferma les yeux, le soleil y resta. Voilà pourquoi le soir, quand le chat se réveille, j'aperçois dans le noir deux morceaux de soleil. (Maurice Carême).
-
Bonjour,Thierry Poma : sûrement pas !N'importe quel ensemble préordonné est une petite catégorie (avec la propriété que quels que soient les objets $a$ et $b$, l'ensemble des flèches de $a$ dans $b$ a au plus un élément).La congruence modulo 2 est un préordre sur $\mathbb Z$. Oui, bon.
-
@GaBuZoMeu: la congruence modulo 2 est un préordre sur $\Z$ : il suffisait d'y penser !
 En tout cas ça change du sempiternel exemple $(\Z,\leqslant)$ ou $(\N,\leqslant)$. merci
En tout cas ça change du sempiternel exemple $(\Z,\leqslant)$ ou $(\N,\leqslant)$. merci  Et que penses-tu de l'intérêt éventuel pour faire aborder à ceux qui ne le connaissent pas encore $Z/2$?
Et que penses-tu de l'intérêt éventuel pour faire aborder à ceux qui ne le connaissent pas encore $Z/2$?
-
Aucun intérêt (mais ce n'est que mon avis).
-
GaBuZoMeu : bonsoir. Tu as entièrement raison. Cependant, la définition me gêne.
Le chat ouvrit les yeux, le soleil y entra. Le chat ferma les yeux, le soleil y resta. Voilà pourquoi le soir, quand le chat se réveille, j'aperçois dans le noir deux morceaux de soleil. (Maurice Carême). -
Pourquoi ?
-
stfj : ça a un intérêt pédagogique pour les gens qui apprennent les catégories, pas pour les gens qui apprennent ce qu'est $\mathbb Z/2$ :-)
Ta catégorie est équivalente à la catégorie discrète sur l'ensemble $\mathbb Z/2$ (i.e. que des flèches identité), et c'est un bon exemple de groupoÏde. C'est aussi un bon exemple pour d'autres phénomènes un peu plus subtils en théorie des catégories mais ce n'est certainement pas ce que tu cherches.
-
@Maxtimax: tu dis "pas pour les gens qui apprennent ce qu'est $\Z/2$". Cependant, je trouve que le dessin que j'ai fourni plus haut avec des flèches de deux couleurs oblige à être plus nuancé : c'est des dessins qu'on pourrait faire faire à des enfants en leur expliquant la règle du jeu, peu importe de coller un vocabulaire savant prématuré dessus. Quand j'étais à la communale, quand j'y songe, on nous faisait faire des trucs assez dingues... Non ?
-
Bof bof. Je trouve que le dessin devient vite fouillis et qu'on n'y voit plus grand chose. Je ne vois pas de raison de nuancer mon avis.stfj, tu viens de te convertir aux catégories. Les nouveaux convertis sont souvent les plus fanatiques.

-
@GaBuZoMeu:
 OUI les Catégories sont grandes !!!
OUI les Catégories sont grandes !!!  mais je pense que tu as trop vite regardé le dessin, peut-être de la condescendance pour les nouveaux convertis
mais je pense que tu as trop vite regardé le dessin, peut-être de la condescendance pour les nouveaux convertis  sur la partie droite du dessin, tout s'ordonne bien, plus le fouillis de la partie gauche...
sur la partie droite du dessin, tout s'ordonne bien, plus le fouillis de la partie gauche... -
Mais tu as juste oublié plein de flèches !(Et pourquoi barres-tu ton 0 ?)
-
@GaBuZoMeu: oui, je n'ai pas indiqué toutes les flèches. Je barre mon $0$ pour le distinguer de la lettre O.
-
Pourtant O et 0 sont déjà très différents. Et $\emptyset$ a un sens technique précis en maths. A se demander si on n'a pas lu de travers certains de tes messages ...Cordialement.
-
@gerard0 : en effet, $0:=\varnothing \text{ et } 1:=\{\varnothing\}$. Quant à la distinction que je fais, c'est un professeur de prépa qui nous proposait de le faire, il y a quelques années maintenant, en nous expliquant que cela venait des informaticiens. D'ailleurs, le signe $:=$ d'affectation vient également des informaticiens je crois. En tout cas, sur le dessin proposé, nulle confusion n'est possible: c'est bien un zéro.
-
bonjour,
@GaBuZoMeu, @Maxtimax : la question continue à me trotter dans la tête. Après tout, je suis enseignant et autant que ce que j'apprends, même si ici c'est pour le plaisir, serve à mes élèves et surtout à moi pour les occuper. Pour tenter malgré vos avis de raviver le débat, je vous propose cette illustration de l'ensemble $\mathbb{Z}/6$ dépourvu de ses structures. Attention : j'ai triché, j'ai mis des couleurs parce que je sais quel résultat je veux, il faudrait laisser les élèves dans le noir un peu avant de finalement les éclairer ou qu'ils s'éclairent eux-mêmes. Qu'en pensez-vous ?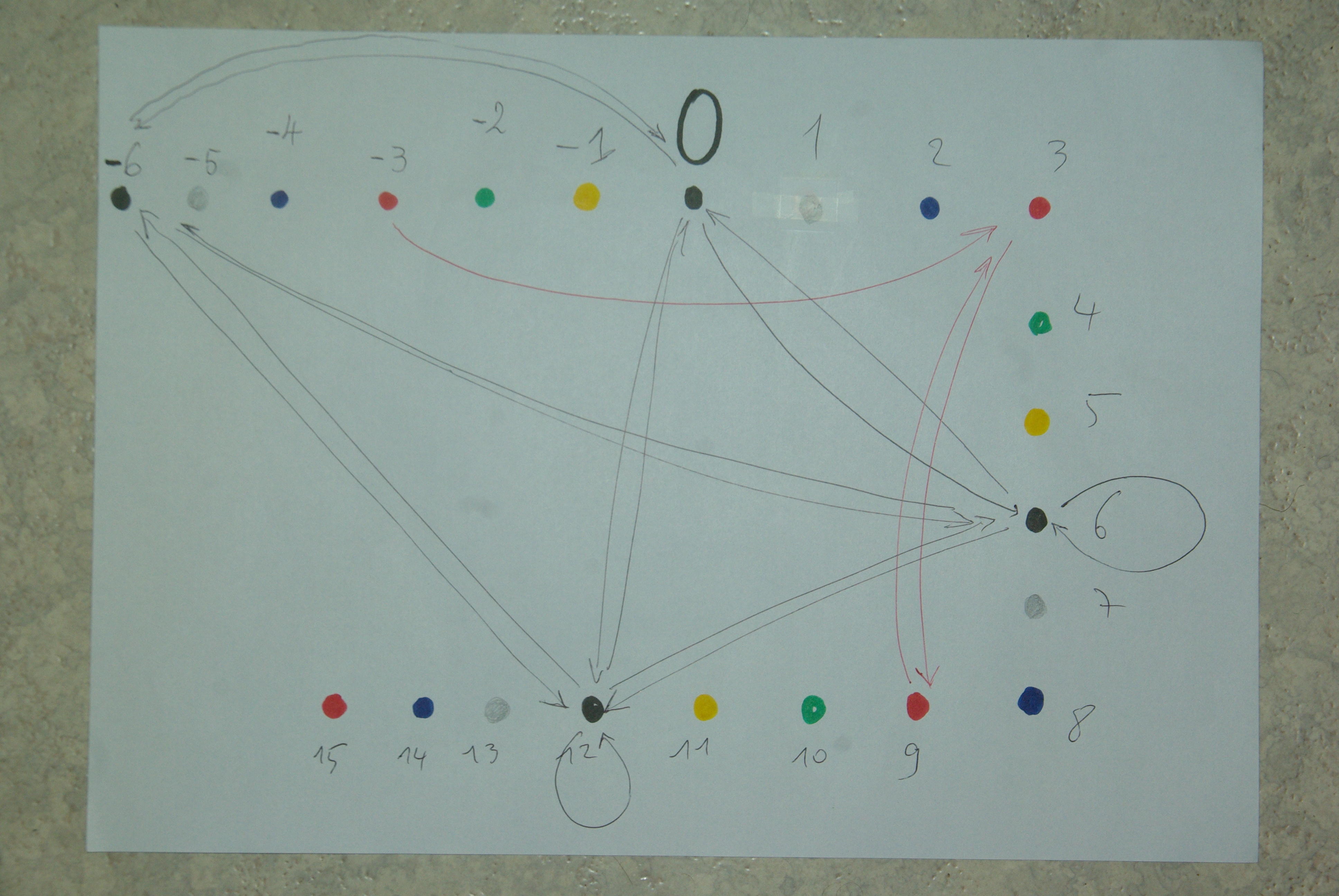
-
Je persiste à penser que ce fouillis de flèches ne sert en rien la compréhension.
-
@GaBuZoMeu : ok.
-
@GaBuZoMeu : bonsoir. Suite à ceci, je n'étais pas dans mon assiette. Ce vendredi 5 août, j'enterrais l'un de mes cousins germains âgé de 58 ans. Le choc a été très brutal et la douleur est encore là. Je voulais seulement te répondre.
Le chat ouvrit les yeux, le soleil y entra. Le chat ferma les yeux, le soleil y resta. Voilà pourquoi le soir, quand le chat se réveille, j'aperçois dans le noir deux morceaux de soleil. (Maurice Carême).
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.8K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 771 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres




