Catalogue de figures presque...
Réponses
-
On parle bien de la même suite. Qu'elle croisse n'est pas contradictoire avec le fait qu'elle ait une limite. Et puis, on ne peut pas conclure de la convergence d'une suite à partir de ses trois premiers termes..
-
Bonsoir, Ludwig,
Je pensais que dans toute suite convergente, la suite |(Si+1 - Si)| des écarts (en valeur absolue) entre deux termes successifs est monotone, strictement décroissante ...
Est-ce faux ? Oui, si je comprends bien ta dernière phrase ...
Bien amicalement
JLB -
Bonjour Jelobreuil.
Pense à la suite 1,0,1/2, 0,1/3,0,1/4,0,...
Et on peut même créer des suites croissantes ayant une limite finie et telles que la valeur absolue de la différence entre deux termes successifs ne soit pas décroissante.
Cordialement. -
Merci Gérard, je reconnais bien volontiers que mon inculture en analyse est plus profonde qu'en géométrie !
Bien cordialement
JLB -
Bonjour,
voici une petite construction directement inspirée par le problème de Ludwig traitant de deux triangles équilatéraux dans le forum Géométrie.
Cela doit pouvoir se traiter en collège ou en lycée .
Tracer le triangle ABC rectangle en C tel que AC = 28 mm et AB = 33 mm .
Tracer le triangle équilatéral BCD , D étant à l'extérieur du triangle ABC .
Mesurer AD .
Après, on peut broder autour de cette figure (calcul de côtés, calcul d'aires, mesure d'angles, etc... ).
AD = 44 mm est la réponse attendue.
Le calcul donne : 43,99967129 mm.
Bien cordialement.
kolotoko -
Bonjour,
un exercice niveau collège.
Dans le plan muni d'un repère orthonormé, on place A(0, 55) ; B(-89, 0); C(34, -199), D(123, -144), E(34, 0) ; F(0, -144).
Tracer les segments AB, BC, CD, DA, AF, BE, EC et FD.
Quelle est la nature du quadrilatère ABCD ?
Quelle est la nature de l'hexagone ABFCDE ?
Calculer l'aire de ABCD et celle de ABFCDE.
Bien cordialement.
kolotoko. -
Bonjour kolotoko,
Ton exercice est plus approprié pour le niveau seconde je pense : calculs de distances dans un repère orthonormé, équations de droites, etc. Mais il est très bien aussi pour le collège, pour expliquer aux élèves qu'il faut se méfier de ce que l'on voit et éviter de conclure précipitamment. Avec GeoGebra on peut leur demander de construire la figure, de tracer la droite $(BC)$ par exemple, puis de zoomer. Et là, surprise ! -
Bonjour,
merci pour la figure.
Le quadrilatère ABCD est un parallélogramme dont un angle vaut 89°, 99531.. ; presque rectangle donc.
L'hexagone convexe ABFCDE a ses côtés opposés parallèles et égaux puisque A + C = B + D = E + F = M( 34, -144).
L'aire du quadrilatère ABCD vaut 24476; l' aire de l' hexagone ABFCDE vaut 24477; on en déduit que la distance de E à AD (ou de F à BC ) vaut 0,004274519..
Les droites AE et BF se coupent à 1 145 251, 602 de l'origine O(0,0) du repère.
De plus la somme des angles ABF et BFE vaut 135° et la somme des angles BAE et AEF vaut 225°.
On peut aussi faire démontrer aux élèves que EF2 = 2 x AB2.
Oui, je suis bien d'accord que cet exercice conviendrait mieux au lycée et qu'on pourrait s'en servir en utilisant Géogébra et ses fonctionnalités.
Bien cordialement.
kolotoko -
Autre possibilité, en utilisant des triangles semblables.
L'unité est le centimètre. $A$, $C$ et $D$ sont alignés.
Question : a-t-on $BD=13?$
Une fois la figure construite à mon avis beaucoup d'élèves vont tomber dans le panneau ($BD=\sqrt{168} \approx 12,96$). Comme la preuve est assez facile c'est un exercice efficace pour les inciter à ne pas conclure juste à partir du dessin. -
Amusant : les nombres choisis sont « fibonacciens ».
-
Et on peut calculer la valeur exacte de $BD$ au collège !

Deux fois Pythagore, En considérant la hauteur issue de $B$ dans le triangle $ABC$. -
Oui ou alors dire « s’ils sont semblables, alors… contradiction ».
-
Ben oui c'est comme ça que je le voyais. Après on contruit la figure avec GGB, qui nous précise que $BD\approx 12,96148..$, ça alors ! Mais qu'est-ce que c'est que cette valeur ?? Et on enchaîne avec Pythagore qui donne la valeur $BD=\sqrt{168}$... imparable !
-
Oui. Ça fait un exercice plutôt riche et dont l’énoncé est assez court.Construction, raisonnement qui conduit à une contradiction (rare en collège) et démonstration directe du calcul de la mesure.
-
Ah oui, en effet j'ai choisi les longueurs à partir de la suite de Fibonacci, je crois d'ailleurs qu'il faut prendre de tels nombres pour que ça marche. Je n'ai pas regardé mais en général, si $AB=BC=CD=F_{n+1}$ et $AC=F_{n}$, alors on doit avoir quelque chose comme $BD^2=F_{n+2}^2 \pm 1$. Si aucun élève ne trouve comment calculer $BD$, pourquoi ne pas utiliser un inverseur pour leur faire voir qu'il propose $\sqrt{168}$ comme forme close ?edit : c'est bien ça, on a $BD^2=F_{n+2}^2 + (-1)^n$

-
Une proposition de suite pour cet exercice : soit $C'$ le symétrique de $C$ par rapport à $D$.
Question : a-t-on $BC'=20$ ?On place $C'$.. évidemment on mesure, on trouve environ $20$, hum.. cette fois on va dire que c'est pas sûr que ça fasse vraiment $20$... sauf que ça fait $20$ pile !Ou alors : soit $E$ le point de la demi-droite $[CA)$ tel que $AE=4$. A-t-on $BE=10$ ? -
oui.
Bien cordialement
kolotoko -
Une remarque d'ordre général : lorsqu'on a sous la main une formule liée à la figure cible où apparaît un nombre irrationnel, on peut utiliser les réduites de ce nombre pour construire une figure presque. Ces réduites étant les meilleures approximations rationnelles possibles, cette figure presque sera elle aussi la meilleure possible (pour les besoins du dessin on se limite à des dimensions pas trop grandes et avec un seul chiffre après la virgule).
Un exemple : on veut construire un triangle presque équilatéral. La hauteur $h$ d'un triangle équilatéral est liée à son côté $c$ par la formule : $$h=\frac{c \sqrt{3}}{2}.$$ Les premières réduites de $\sqrt{3}$ sont $2$, $5/3$, $7/4$, $19/11$, $26/15$, $71/41$, $97/56$ et $265/153$. $26,5$ c'est trop grand pour une feuille au format A4, on prendra donc un triangle $ABC$ isocèle en $A$ tel que $BC= 11,2$ et dont la hauteur issue du sommet principal mesure $9,7$. Question : est-il équilatéral ? Non, mais $AB=AC=\sqrt{125,45}\approx 11,2004$. Et pour cette consigne on ne peut pas faire une meilleure approximation compte tenu des contraintes liées au dessin.
-
Génial le triangle isocèle de base 8 et de hauteur 7; ça fait longtemps que je cherchais un triangle dans les nœuds du quadrillage qui paraisse équilatéral bien que ce soit impossible (puisque $\sqrt3\notin \mathbb Q$ ) : voilà, je l'ai. Merci.
Remarque : (1) si au lieu de prendre le cm comme unité, on prend les carreaux de $8$mm, on lit $6.4 cm$ partout : c'est encore plus bluffant; et le triangle est rapidement construit avec le quadrillage ;
(2) le côté est $\sqrt{65}$ ; la variation par rapport au triangle équilatéral est $\frac{\sqrt{65}}{\sqrt{64}}\approx 1+\frac12.\frac{1}{64}$ soit plus petite que $1\%$.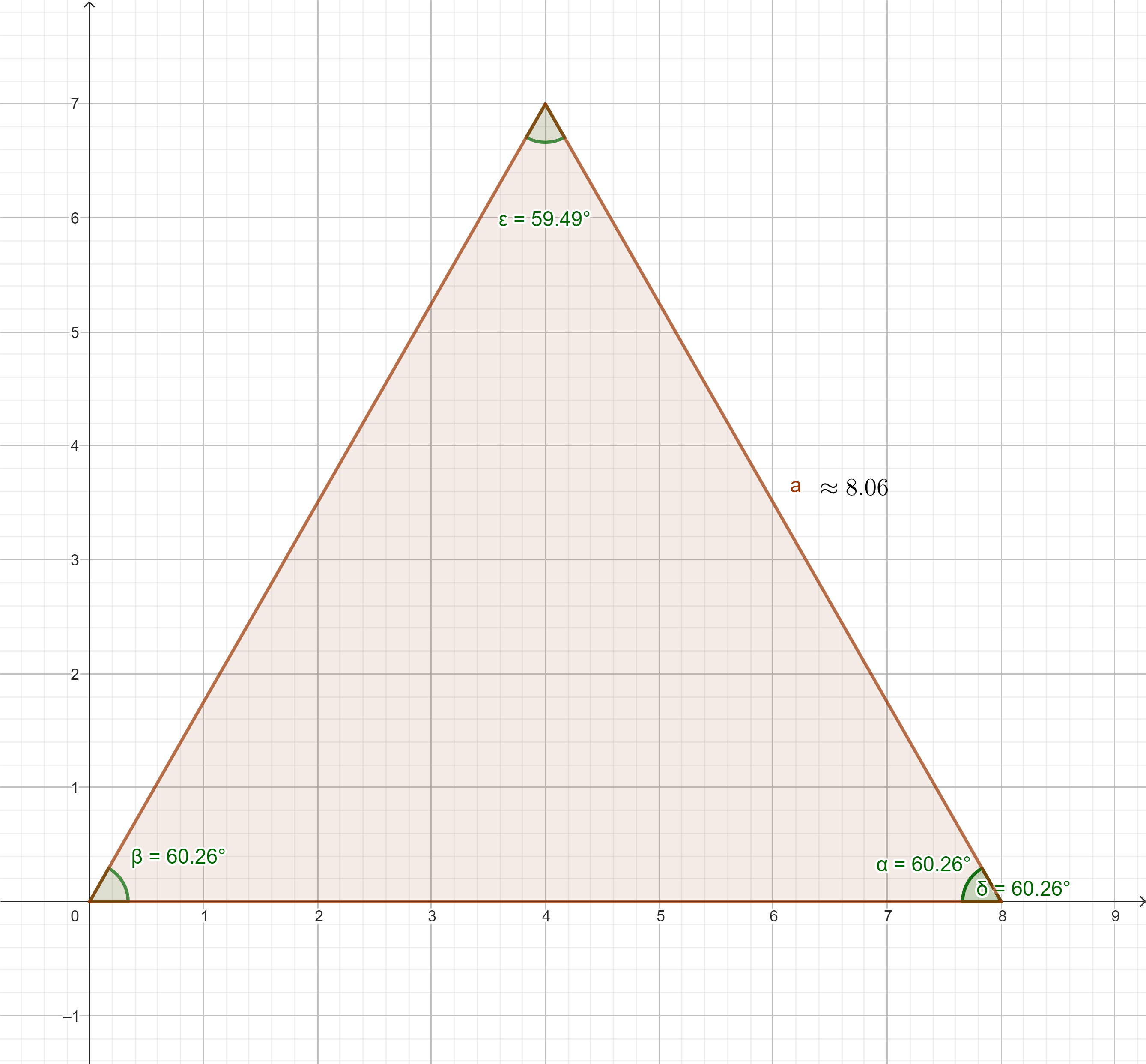
Je l'ai expérimenté avec mes élèves de 6è; ça marche du tonnerre en lien avec ce document par exemple. -
Tu prends les triplets pythagoriciens et tu fais de très légères variations d'un ou deux entiers composant le triplet : je m'amusais ainsi à obtenir des angles de 90.004° avec la formule d'Al Kashi traçables par des élèves. Record à battre

-
Oui, ou tu dessines un triangle rectangle sur une feuille et tu mesures ses côtés au mm près. Une question en lien avec ton record : en raison des contraintes liées au dessin avec les instruments on considère les triangles non rectangles dont les dimensions sont mettons comprises entre 5 et 12 cm et qui ont au plus un chiffre après la virgule. Quels sont parmi ces triangles ceux dont un angle est le plus proche de 90° ? Un programme devrait rapidement venir à bout de cette question.
-
J'obtiens comme record $(148,88,119)$ (en millimètres), pour un angle de $90{,}0027^\circ$.
sage: d=1. sage: for a in range(30,151): ....: for b in range(30,151): ....: for c in range(abs(b-a)+1,a+b): ....: u = (a^2-b^2-c^2)/2/b/c ....: if abs(u)>1e-8 and abs(u)
-
Merci Math Coss. J'aime bien ces exercices où plane un autre savoir, savoir inexplicable aux élèves car hors-programme ou trop compliqué, mais qu'on peut présenter comme une énigme et énerver les curieux : il se trouve, chers élèves, qu'on peut calculer les angles de ce triangle (quoi, comment ?? se demande l'élève qui aime explorer)..., et cet angle-là mesure environ $90,0027°$... Oui mais bien sûr ! s'amuse une autre élève qui adore mener l'enquête, car un truc aussi proche d'un angle droit il y a forcément du voulu là-dedans, mais alors.. comment est-ce possible... etc etc..
-
L'irrationalité de $\sqrt{3}$ rappelée par stfj permet aussi de montrer qu'une construction relative au célèbre puzzle de Dudeney n'est qu'approchée, une figure presque elle aussi.
-
Bonjour,Soit le triangle ABC avec (a = 148 , b = 119 , c = 88 ) où b^2 + c^2 = 1 + a^2.En appliquant Al-Kashi (règle du cosinus), je trouve pour mesure d'angle en degré .A = 89,99726433B = 53,51899865C = 36,48373701B + C = 90,0273566il est clair que ce triangle ne peut pas être rectangle car a est pair alors que b et c sont impair et pair.Bien cordialement.kolotoko
-
D'accord. Apparemment, j'ai fait une erreur de signe dans la formule d'Al Kashi (définition de $u$ ci-dessus). Je refais un essai pour copier le code (en rectifiant l'erreur).
sage: d = 1. sage: for a in range(30,151): ....: for b in range(30,151): ....: for c in range(abs(b-a)+1,a+b): ....: u = (b^2+c^2-a^2)/2/b/c ....: if abs(u)>1e-8 and abs(u)
-
Pour un triangle plus petit, par exemple avec des côtés entre 3 et 8 cm, j'ai demandé à Chat GPT d'écrire un programme en python :import math# une fonction pour calculer l'angle A dans un triangle ABCdef angle_A(a,b,c):cos_A = (b**2 + c**2 - a**2) / (2*b*c)return math.acos(cos_A)# liste pour stocker les triangles et leur angle Atriangles = []# parcourez toutes les combinaisons possibles de côtésfor a in range(30, 81):for b in range(30, 81):for c in range(30, 81):if (a+b)>c and (a+c)>b and (b+c)>a: #condition pour un triangle valideA = angle_A(a,b,c)if math.degrees(A) != 90:triangles.append((a,b,c, math.degrees(A)))# trouver le triangle avec angle A le plus proche de 90min_diff = float('inf')best_triangle = ()for triangle in triangles:diff = abs(90 - triangle[3])if diff < min_diff:min_diff = diffbest_triangle = triangleprint("Le triangle avec l'angle le plus proche de 90 degrés est : ", best_triangle)
Puis j'ai utilisé un compilateur en ligne pour trouver : $(78, 46, 63, 89.99011459975893)$. -
Voici la figure du $(78,46,63)$ obtenue avec geogebra (chatGPT est une puissante aide pour un prof)
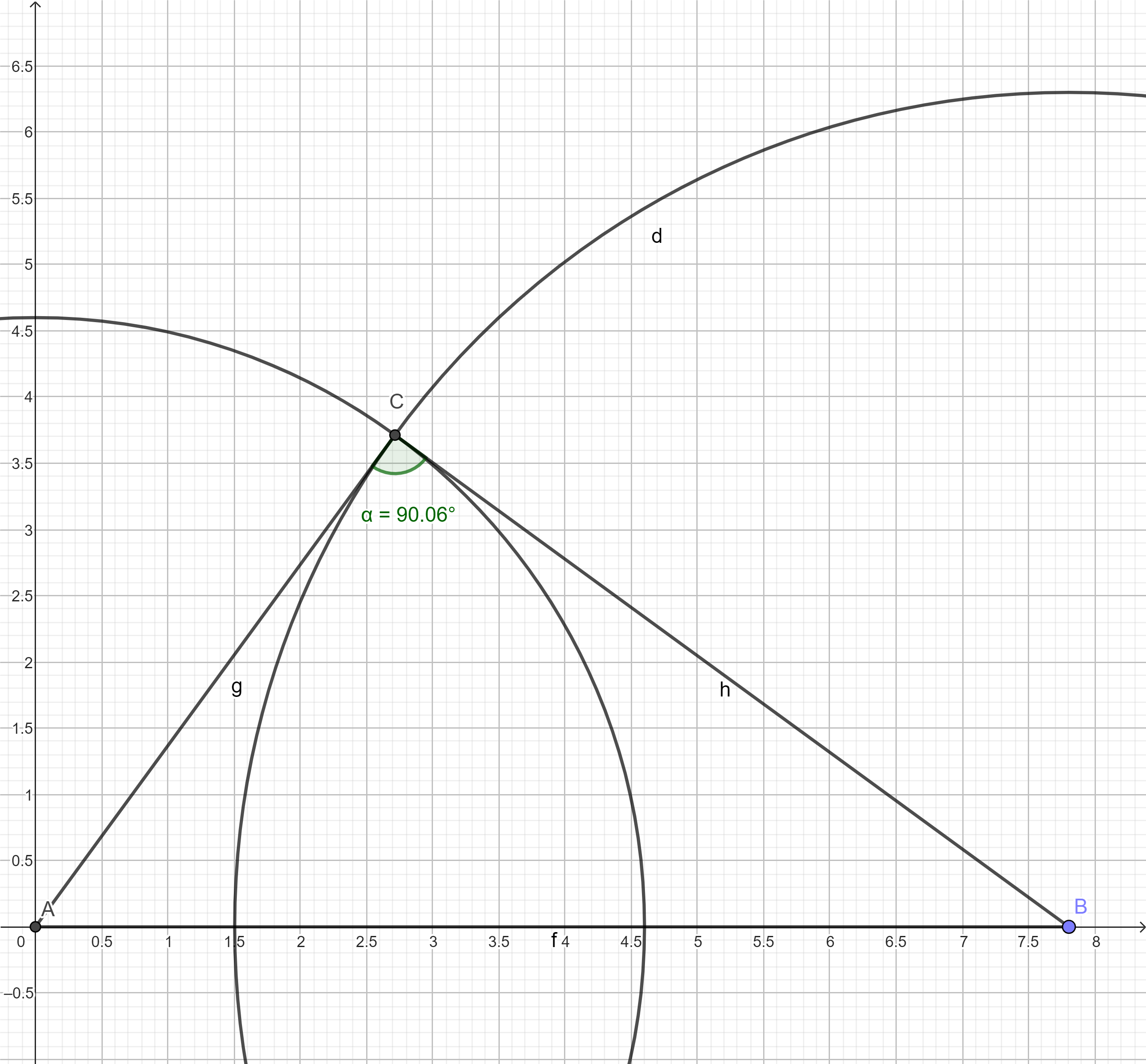
-
bonjour,l'angle presque droit mesure 89,990114... degrés et non 90,06 degrés .Bien cordialement.kolotoko
-
Pour ce problème d'optimisation il semble que la solution vérifie toujours $a^2+b^2=c^2 +1$. Pourquoi ?
Si on cherche le triangle optimal pour des longueurs comprises entre $1$ et $n$ le côté le plus long $c$ est très proche de la borne supérieure, et on doit avoir $c/n\underset{\infty}{\sim}1$.
Et la solution correspond au maximum du produit $ab$, puisqu'il s'agit de minimiser $(a^2+b^2-c^2)/(2ab)$. On est amené à étudier la fonction $x \sqrt{n^2-x^2}$ pour trouver qu'il y a sans doute convergence vers le triangle isocèle rectangle $a=b=n \sqrt{2}/2$. -
Bonjour,
une simple remarque : le triangle de Math Coss ( a =148; b = 119; c = 88 ) et le triangle de Ludwig ( a = 78; b = 63; c = 46 ) sont obtenus en faisant n = 29 et n = 15 dans les formules a = 5n + 3; b = 4n + 3; c = 3n +1.Bien cordialement.kolotoko -
Malheureusement tes formules ne marchent pas pour par exemple $n= 210$. Existe-t-il seulement des formules simples pour déterminer les longueurs des côtés du triangle solution ? Possible que la contrainte de maximalité l'emporte sur celles liées aux entiers, pour $n$ assez grand. Et qu'on ait quelque chose du genre partie entière d'une division... un truc modulo $4$... oula.. je fais beaucoup trop dans l'approximatif !
-
Bonsoir,
les triangles a = 5n + 3; b = 4n + 3; c = 3n +1 tendent vers la forme du triangle rectangle (5, 4, 3) quand n tend vers l'infini et on a a^2 +1 = b^2 + c^2 quelque soit la valeur de n.
Pour n = 210 l'angle A vaut 89,9999461 degrés.
Bien cordialement.
kolotoko -
Je me suis mal exprimé, désolé. On ne parle pas de la même chose, je voulais parler des triangles dont les longueurs des côtés sont plus petites ou égales à $210$. Si tu prends les triangles dont les côtés sont plus petits ou égaux à $5 \times 210 + 3$ alors je crois que ton triangle n'est pas optimal. Peut-être faut-il considérer des familles de triangles.
-
Bonsoir,
pour le catalogue de Ludwig, je propose ce petit exercice de niveau collège.Soit le trapèze rectangle ABCD suivant :
grande base AB = 34 mm ; petite base AC = 14 mm ; hauteur AD = 31 mm.
Construire le trapèze.
Mesurer les diagonales.
Calculer les diagonales.
Le triangle ABC est-il isocèle ?Bien cordialement.
kolotoko -
Bonsoir à tous,@kolotoko : la petite base est CD et non pas AC.
Autrement, c'est pas mal ! le calcul donne 34,0147 mm pour la diagonale BC ...Bien cordialement, JLB -
Ce n’est pas tout à fait dans ce fil mais ça peut être intéressant.L’exercice se fait bien. Mais si on va un peu plus loin, et que l’on demande de coder les angles de même mesure, on trouve qu’il y a un truc qui cloche : K appartient à [IL].Pour rentrer dans le fil, on pourrait faire tracer cette figure en vraie grandeur et la question serait de savoir si des points sont ou non alignés.Autre idée : la figure peut aussi être une représentation d’une pyramide de sommet K. Dans ce cas, pas de problème.Ces discussions m’apparaissent intéressantes.C’est dans Transmath Cycle 4
 Une remarque typographique : dans beaucoup de manuels, une police similaire à de l’ARIAL a été adoptée. Mais pour le « i Majuscule », ils ont dû changer la police et prendre un genre « Times New Roman ». Le « i » droit peut être confondu parfois avec un « L minuscule ».
Une remarque typographique : dans beaucoup de manuels, une police similaire à de l’ARIAL a été adoptée. Mais pour le « i Majuscule », ils ont dû changer la police et prendre un genre « Times New Roman ». Le « i » droit peut être confondu parfois avec un « L minuscule ».
En effet : voici un I et voici un l .Je crois que les polices avec empattements gênent certains lecteurs comme des dyslexiques. -
C'est la raison pour laquelle le symbole international pour le litre est L et pas l. En pratique, cela devrait inciter à éviter certaines lettres.
-
Bonjour,
je remercie jelobreuil pour avoir signalé et corrigé l'erreur dans mon précédent message.
On a bien AC = 34,0147...
On a aussi BD = 46,0108...
On pourrait, pour les amoureux de la trigonométrie, proposer l'exercice suivant.
Soit ABCD un quadrilatère vérifiant : AB = AC = 34 ; BD = 46 ; DC = 14 et AD = 31.
Calculer BC.
Bien cordialement.
kolotoko -
On pourrait dire Dom que pour ton problème la figure à main levée est, dans un sens, presque la figure correcte. Pas une figure presque, mais presque la figure. C'est très intéressant en effet. En cours de résolution du problème on est amené à rectifier la première figure donnée (on peut aussi imaginer que cette figure à main levée est faite par les élèves), ce qui crée d'autres questions, oblige à un repositionnement et à revisiter les questions déjà traitées. Fabriquons des problèmes !
On peut par exemple envisager une double rectification, pourquoi pas. Par exemple un point qui sur la figure de départ n'est pas sur une droite et qui en fait s'avère y appartenir, et puis qui finalement appartient aussi à une autre droite et donc c'est leur point d'intersection.
-
Dom a dit :Je crois que les polices avec empattements gênent certains lecteurs comme des dyslexiques.Pas forcément, en fait.Le mieux est de demander.
Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
Bonjour,il y a deux solutions au calcul de BC selon que le quadrilatère est ABCD (diagonales AC et BD ) ou ABDC (diagonales AD et BC) .On trouve BC = 36,8646342609 pour ABCD et 57,1226730939 pour ABDC.Leurs carrés valent presque 1359 et presque 3263 .Bien cordialement.kolotoko
-
Bonjour,à propos de la figure proposée par Dom :on pourrait demander à des collégiens de tracer le triangle MIL avec MI = 12 cm ; IL = 36 cm , ML = 30 cm puis de tracer le cercle de centre M et de rayon 10 cm ainsi que le cercle de centre L et de rayon 25 cm.Ils verront bien que ces deux cercles se coupent en deux points : K1 situé sur le segment |IL] et K2 symétrique de K1 par rapport au segment [ML] .Ils déduiront que IK1 = 36 - 25 = 11 cm.Le calcul de IK2 donne 21,7255609824 cm et on a IK2 ^2 = 472.Je ne sais pas si une démonstration est envisageable pour un si jeune public.Bien cordialement.kolotoko
-
Autre construction d'un quasi triangle équilatéral, à partir d'un quadrillage : on considère les triangles ayant pour sommets des points à coordonnées entières et comprises entre $0$ et un entier $n$ donné. On cherche à minimiser la somme des valeurs absolues des différences entre les angles et $60°$. Avec un programme j'ai déterminé les coordonnées des sommets du triangle solution (à symétrie près) pour les premières valeurs de $n$ :
${(0, 0), (1, 2), (2, 0)}$
${(0, 1), (3, 4), (4, 0)}$
${(0, 0), (3, 5), (6, 0)}$
${(0, 2), (5, 7), (7, 0)}$
${(0, 0), (4, 7), (8, 0)}$
${(0, 3), (8, 11), (11, 0)}$
${(0, 4), (11, 15), (15, 0)}$
$ {(0, 7), (19, 26), (26, 0)}$
On reconnait les entiers intervenant dans les réduites de la racine carrée de $3$.
Mais quelle est la loi exacte de formation de la suite de ces points ?
-
Bonsoir,Ludwig a dit : https://les-mathematiques.net/vanilla/index.php?p=/discussion/comment/2405588/#Comment_2405588Pour ce problème d'optimisation il semble que la solution vérifie toujours $a^2+b^2=c^2 +1$. Pourquoi ?
Si on cherche le triangle optimal pour des longueurs comprises entre $1$ et $n$ le côté le plus long $c$ est très proche de la borne supérieure, et on doit avoir $c/n\underset{\infty}{\sim}1$.
Et la solution correspond au maximum du produit $ab$, puisqu'il s'agit de minimiser $(a^2+b^2-c^2)/(2ab)$. On est amené à étudier la fonction $x \sqrt{n^2-x^2}$ pour trouver qu'il y a sans doute convergence vers le triangle isocèle rectangle $a=b=n \sqrt{2}/2$.
il me semble que les triangles correspondants à cette problématique sont les triangles c ; b ; a, où b = c = 1 ; 5 ; 29 ; 169 ; 985 ; .... suite A001653 de O.E.I.S.et a = 1 ; 7 ; 41 ; 239 ; 1393; ... suite A002315 de O.E.I.S.Pour des élèves, on peut leur proposer un exercice sur le triangle 5 ; 5; 7 ou sur le triangle 29 ; 29 ; 41 qui sont isoçèle et presque rectangle.Bien cordialement.kolotoko -
Merci kolotoko je vais regarder ces suites.
Pour mon problème de construction d'un triangle quasi équilatéral à partir d'un quadrillage, il me semble que les coordonnées des sommets d'un triangle optimal sont du type $(0,a)$, $(b,a+b)$ et $(a+b,0)$, où les nombres $a$ et $b$ se déduisent des réduites de la racine carrée de $3$. Colonne de gauche les dénominateurs des réduites, à droite les numérateurs correspondants. Le chemin bleu, qui se répète, donne les nombres $a$ successifs : 1, 2, 3, 4, 7, 11, 15, 26..

Pour avoir les nombres $b$ correspondants il faut faire des additions, mais pas toujours : somme première ligne 1 + 2 = 3, puis on prend le 5 de la deuxième ligne ; somme deuxième ligne 3 + 5 = 8, somme de la troisième 4 + 7 = 11 puis on prend le 19 de la 4ème. Et on recommence deux additions des lignes suivantes et on prend le numérateur de la ligne suivante, etc.
On obtient :
${(0, 1), (3, 4), (4, 0)}$
${(0, 2), (5, 7), (7, 0)}$
${(0, 3), (8, 11), (11, 0)}$
${(0, 4), (11, 15), (15, 0)}$
${(0, 7), (19, 26), (26, 0)}$
Cela est vérifié expérimentalement : ces triangles minimisent la somme des écarts des angles à 60°. Et au fur et à mesure que la taille du quadrillage augmente, cette somme tend vers zéro.
Il y a sûrement une façon plus simple de définir ces suites.
oui, voir A140827 et A254308. -
Bonjour,
on a donc des triangles presque équilatéraux avec un point sur l'axe des x et un sur l'axe des y .Mais il serait plus simple de positionner A (0, y) ; B (-x,0) ; C (x, 0) avec :y : 1 ; 2 ; 5 ; 7 : 19 ; 26 ; 71 ; 97 ; ... suite A002531x : 1 ; 1 ; 3 ; 4 ; 11 ; 15 ; 41 ; 56 ; ... suite A002530Bien cordialement.
kolotoko -
Ah oui merci, je cherchais ces autres triangles. En plus je crois que lorsque la taille du quadrillage est fixée ce sont tes triangles les plus petits. Mon triangle qui réalise le même minimum (il y en a toujours un d'ailleurs) a besoin d'un peu plus d'espace. Mais je ne suis pas sûr, à voir. Bonne journée, Ludwig.
-
Bonjour,
voici un petit exercice piégé.1) Soit ABCDEF l'hexagone vérifiant AB = AF = 7 ; CB = CD = 16 ; ED = EF = 23 ; AC = 22 ; CE = 30 ; EA = 27.
Construire cet hexagone en indiquant la procédure suivie.
2) Comment justifier que l'aire de l'hexagone ABCDEF est le double de l'aire du triangle ACE .Bien cordialement.
kolotoko.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres




