Premiers classés par niveau
Bonjour,
Je vous propose une conjecture dont les définitions seront données un peu plus bas :
Conjecture 9 : les nombres premiers classés par niveau se raréfient parmi les nombres premiers.
Précisions importantes : à part $p(1)=2$, $p(2)=3$ et $p(4)=7$ les nombres premiers sont soit classés par poids soit par niveau. Les nombres premiers classés par poids ont par définition un saut (première différence) inférieur à $\sqrt{p(n)}$
Mes questions sont :
- Cette conjecture est-elle dure à prouver ? (je pense que oui)
- Cette conjecture est-elle intéressante concernant la répartition des nombres premiers ? (je pense que oui)
- Quelles sont les relations de cette conjecture avec d'autres conjectures célèbres comme la conjecture de Legendre et l'hypothèse de Riemann ?
Je mets les définitions de la décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ sur le forum pour que vous n'ayez pas à sortir mais vous pouvez les retrouver sur la page de la décomposition sur l'OEISWiki et dans mon preprint (arXiv:0711.0865)
Définitions de la décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ :
Soit $\scriptstyle {\{a(n)\}}_{n=i_\min}^{\infty} \,$ une suite d'entier strictement croissante.
Le saut (première différence, écart) :
$d(n) := a(n+1) - a(n). \,$
$l(n) := \begin{cases} a(n) - d(n) & \text{si } a(n) - d(n) > d(n), \\ 0 {\rm ~sinon}. \end{cases} \,$
Définition alternative avec la fonction $mod$ :
$l(n) := {\rm plus~~grand~} l {\rm~tel~que~} a(n+1) = a(n) + a(n){\rm~}mod{\rm~}l, {\rm~ou~} 0 {\rm~si~un~tel~} l {\rm~n'existe~pas.~}$
Le poids :
$k(n) := \begin{cases} {\rm plus~petit~} k > d(n) {~t.q.~} k|l(n), \\ 0 {\rm ~si~} l(n) = 0. \end{cases} \,$
Définition alternative avec la fonction $mod$ :
$k(n) := {\rm plus~petit~} k {\rm~tel~que~} a(n+1) = a(n) + a(n){\rm~}mod{\rm~}k, {\rm~ou~} 0 {\rm~si~un~tel~} k {\rm~n'existe~pas.~}$
Le niveau :
$L(n) := \begin{cases} \frac{l(n)}{k(n)} & \text{si } k(n) > 0, \\ 0 & \text{si } k(n) = 0. \end{cases} \,$
Critère de décomposition :
La décomposition est possible si et seulement si $a(n+1) < \frac{3}{2} \times a(n) \,$
Une décomposition unique :
Le poids est le plus petit tel que dans la division euclidienne de $a(n)$ par son poids, le quotient est le niveau et le reste est le saut et nous avons : $a(n) = k(n) \times L(n) + d(n) = {\rm poids} \times {\rm niveau} + {\rm saut} \,$
Principe de classification :
Si pour $a(n)$, $l(n) = k(n) = L(n) = 0 \,$ alors $a(n)$ n'est pas classé.
Si pour $a(n)$, $k(n) > L(n) \,$ alors $a(n)$ est classé par niveau sinon $a(n)$ est classé par poids.
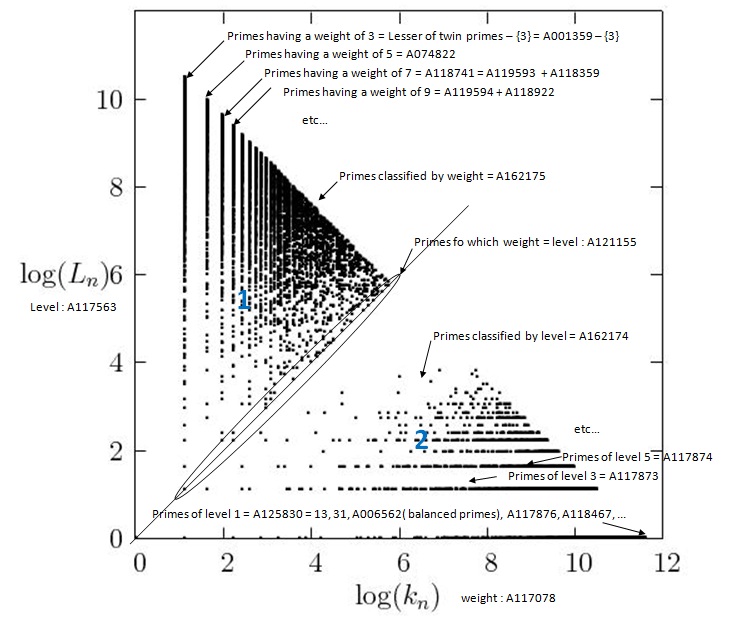
La décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ des entiers naturels est le crible d’Ératosthène : les entiers naturels classés par poids sont les $composés + 1$ et ceux classés par niveau sont les $premiers + 1$
Ci-dessous un graphique de la décomposition des nombres premiers :
Cela fait pas mal de temps que j'ai compris que je ne faisais pas des maths car faire des mathématiques c'est démontrer des propositions or je ne fais que monter une façon de décomposer les nombres. Dans mon preprint, ce ne sont pas les théorèmes et lemmes qui sont importants mais les définitions.
Concernant la question de savoir si les maths sont inventées ou découvertes, j'avais trouvé un élément de réponse intéressant sur un blog dont je ne me souviens plus de l'adresse : les définitions sont inventées et les théorèmes découverts. Donc dans mon cas j'ai inventé la décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ mais je n'ai rien découvert.
Merci d'avoir pris le temps de lire ce message.
Bon Dimanche,
Edit 12/08/2021 : correction des liens des images, le forum ne suit plus les redirections.
Je vous propose une conjecture dont les définitions seront données un peu plus bas :
Conjecture 9 : les nombres premiers classés par niveau se raréfient parmi les nombres premiers.
Précisions importantes : à part $p(1)=2$, $p(2)=3$ et $p(4)=7$ les nombres premiers sont soit classés par poids soit par niveau. Les nombres premiers classés par poids ont par définition un saut (première différence) inférieur à $\sqrt{p(n)}$
Mes questions sont :
- Cette conjecture est-elle dure à prouver ? (je pense que oui)
- Cette conjecture est-elle intéressante concernant la répartition des nombres premiers ? (je pense que oui)
- Quelles sont les relations de cette conjecture avec d'autres conjectures célèbres comme la conjecture de Legendre et l'hypothèse de Riemann ?
Je mets les définitions de la décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ sur le forum pour que vous n'ayez pas à sortir mais vous pouvez les retrouver sur la page de la décomposition sur l'OEISWiki et dans mon preprint (arXiv:0711.0865)
Définitions de la décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ :
Soit $\scriptstyle {\{a(n)\}}_{n=i_\min}^{\infty} \,$ une suite d'entier strictement croissante.
Le saut (première différence, écart) :
$d(n) := a(n+1) - a(n). \,$
$l(n) := \begin{cases} a(n) - d(n) & \text{si } a(n) - d(n) > d(n), \\ 0 {\rm ~sinon}. \end{cases} \,$
Définition alternative avec la fonction $mod$ :
$l(n) := {\rm plus~~grand~} l {\rm~tel~que~} a(n+1) = a(n) + a(n){\rm~}mod{\rm~}l, {\rm~ou~} 0 {\rm~si~un~tel~} l {\rm~n'existe~pas.~}$
Le poids :
$k(n) := \begin{cases} {\rm plus~petit~} k > d(n) {~t.q.~} k|l(n), \\ 0 {\rm ~si~} l(n) = 0. \end{cases} \,$
Définition alternative avec la fonction $mod$ :
$k(n) := {\rm plus~petit~} k {\rm~tel~que~} a(n+1) = a(n) + a(n){\rm~}mod{\rm~}k, {\rm~ou~} 0 {\rm~si~un~tel~} k {\rm~n'existe~pas.~}$
Le niveau :
$L(n) := \begin{cases} \frac{l(n)}{k(n)} & \text{si } k(n) > 0, \\ 0 & \text{si } k(n) = 0. \end{cases} \,$
Critère de décomposition :
La décomposition est possible si et seulement si $a(n+1) < \frac{3}{2} \times a(n) \,$
Une décomposition unique :
Le poids est le plus petit tel que dans la division euclidienne de $a(n)$ par son poids, le quotient est le niveau et le reste est le saut et nous avons : $a(n) = k(n) \times L(n) + d(n) = {\rm poids} \times {\rm niveau} + {\rm saut} \,$
Principe de classification :
Si pour $a(n)$, $l(n) = k(n) = L(n) = 0 \,$ alors $a(n)$ n'est pas classé.
Si pour $a(n)$, $k(n) > L(n) \,$ alors $a(n)$ est classé par niveau sinon $a(n)$ est classé par poids.
La décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ des entiers naturels est le crible d’Ératosthène : les entiers naturels classés par poids sont les $composés + 1$ et ceux classés par niveau sont les $premiers + 1$
Ci-dessous un graphique de la décomposition des nombres premiers :

Cela fait pas mal de temps que j'ai compris que je ne faisais pas des maths car faire des mathématiques c'est démontrer des propositions or je ne fais que monter une façon de décomposer les nombres. Dans mon preprint, ce ne sont pas les théorèmes et lemmes qui sont importants mais les définitions.
Concernant la question de savoir si les maths sont inventées ou découvertes, j'avais trouvé un élément de réponse intéressant sur un blog dont je ne me souviens plus de l'adresse : les définitions sont inventées et les théorèmes découverts. Donc dans mon cas j'ai inventé la décomposition en ${\rm poids} \times {\rm niveau} + {\rm saut} \,$ mais je n'ai rien découvert.
Merci d'avoir pris le temps de lire ce message.
Bon Dimanche,
Edit 12/08/2021 : correction des liens des images, le forum ne suit plus les redirections.
Réponses
-
Plus récemment, un physicien E.Wigner a modélisé les niveaux d'énergie des systèmes atomiques. Cette proposition qui lie les valeurs propres de $\zeta(s)$ aux niveaux quantiques des systèmes atomiques est désormais connue sous le nom de la loi empirique dite de: Montgomery-Odlyzko. Autrement, le théorème de raréfaction des nombres premiers démontrée par A-M. Legendre et établi dès1808 dit que : $\lim_{n \to +\infty}\frac{\pi(n)}{n}\ =\ 0.$
-
Bonjour,
150 suites décomposées en poids × niveau + saut :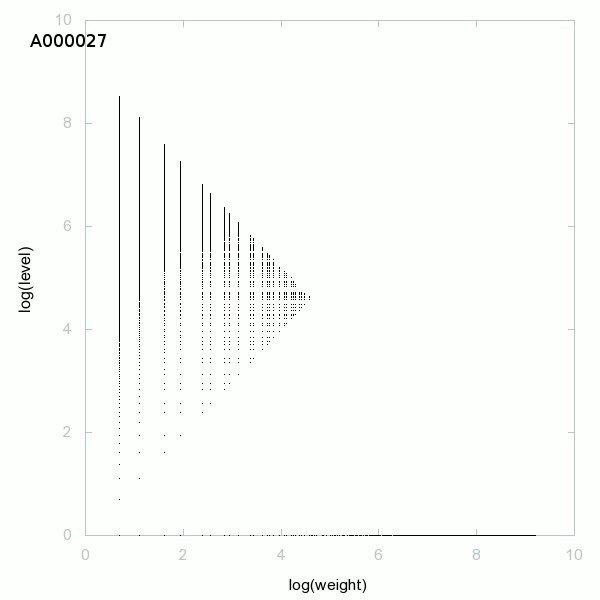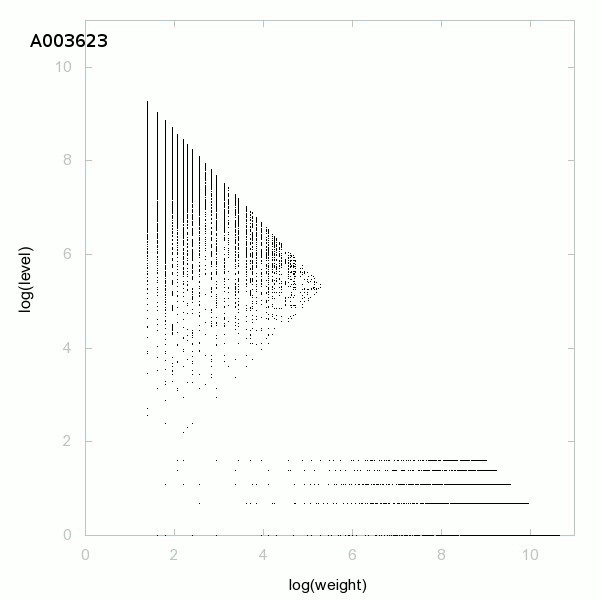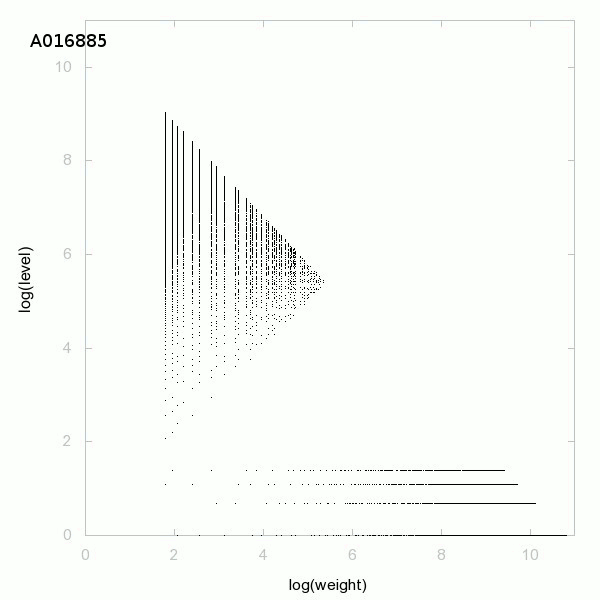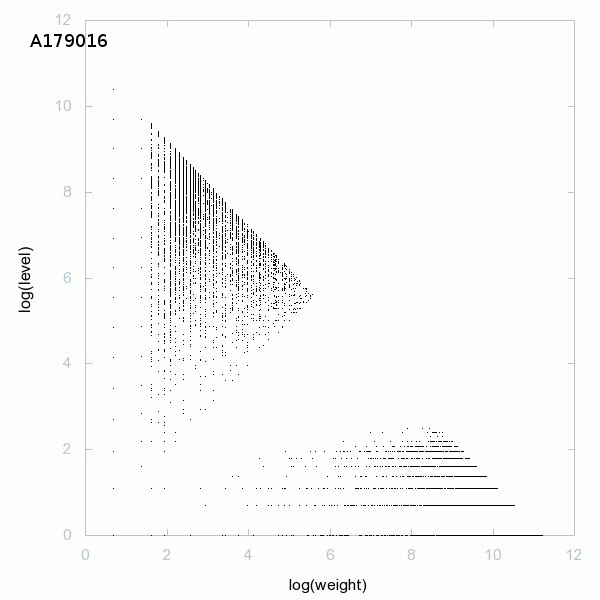
La plupart des crackpots prétendent prouver des conjectures célèbres, moi, je propose juste une nouvelle façon de voir les nombres.
Edit 12/08/2021 : correction des liens des images, le forum ne suit plus les redirections. -
Bonjour,
Ma première suite : A117078 (celle dont tout découle - 10 ans aujourd'hui).
La décomposition en poids × niveau + saut des nombres premiers en 3D (WebGL-three.js).
Un album Google+ des graphiques 2D des 400 suites que j'ai décomposées.
Mes questions du premier post tiennent toujours.
Bonne journée, -
Bonjour,
La décomposition en $poids × niveau + saut$ est une décomposition d'entier positif dans une suite. Le poids est le plus petit tel que dans la division euclidienne d'un nombre par son poids, le reste et le saut (première différence, écart). Le quotient est le niveau. Donc pour décomposer $a(n)$, on a besoin de $a(n+1)$ avec $a(n+1)>a(n)$ (suite strictement croissante) et la décomposition est possible si $a(n+1)<\frac{3}{2}a(n)$.
La décomposition en $poids × niveau + saut$ des entiers naturels est le crible d’Ératosthène. Pour les entiers naturels, le poids est plus plus petit facteur premier de $(n - 1)$ et le niveau est le plus grand diviseur propre de $(n - 1)$. Les entiers naturels classés par niveau sont les $(premiers + 1)$ et les entiers naturels classés par poids sont les $(composés + 1)$.
Pour les nombres premiers, cette décomposition conduit à une nouvelle classification des nombres premiers. Les nombres premiers classés par poids suivent le conjecture de Legendre et je conjecture que ceux classés par niveau se raréfient. Je pense que cette conjecture est très importante pour la distribution des nombres premiers. Il est facile de voir et de prouver que les plus petits des nombres premiers jumeaux ($>3$) ont un poids de $3$. Donc la conjecture des nombres premiers jumeaux peut se réécrire : il y a une infinité de nombres premiers qui ont un poids de $3$.
Je ne suis pas mathématicien donc je décompose des suites pour promouvoir ma vision des nombres, maintenant 400 suites décomposées sur mon site avec les 500 premiers termes et des graphiques en 3D (webGL - three.js). En faisant ces décompositions, j'applique une sorte de crible sur chacune de ces suites. En un sens, je trouve les composés (nombres classés par poids) et les premiers (nombres classés par niveau) de chacune de ces suites.
Un album imgur.
Bonne journée,
R.E. -
Bonjour,
Il y a maintenant 800 suites décomposées en poids × niveau + saut sur mon site web :
https://decompwlj.com
Cordialement, -
Bonjour,
Je sais bien que ça n'intéresse pas grand monde mais je voulais vous dire qu'il y a 1000 suites décomposées en $poids × niveau + saut$ sur mon site web. Avant de continuer, j'aimerais avoir une vérification indépendante de mes données. Si le cœur vous en dit, il y a un dump complet de ma base de données sur la page d'accueil (.sql.zip, ~105 Mo, table centrale "sequences" et une table par suite).
Cordialement, -
C'est vraiment injuste, les autres crackpots ont des dizaines de réponses et moi, aucune.
Je viens avec un preprint sur arXiv, des suites dans l'OEIS et rien.
Suite à l'intervention de G.F., j'ai fait une page sur la décomposition en poids × niveau + saut sur la Wikiversité :
https://fr.wikiversity.org/wiki/Recherche:Décomposition_en_poids_×_niveau_+_saut
Effectivement je n'ai rien prouvé de sensationnel mais cela ne vous intéresse pas ? Cela ne vous fait pas poser des questions ? C'est un nouveau théorème fondamental de l'arithmétique !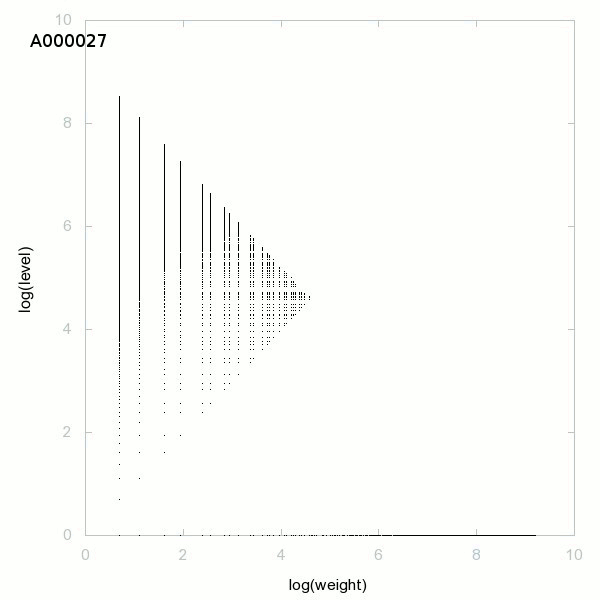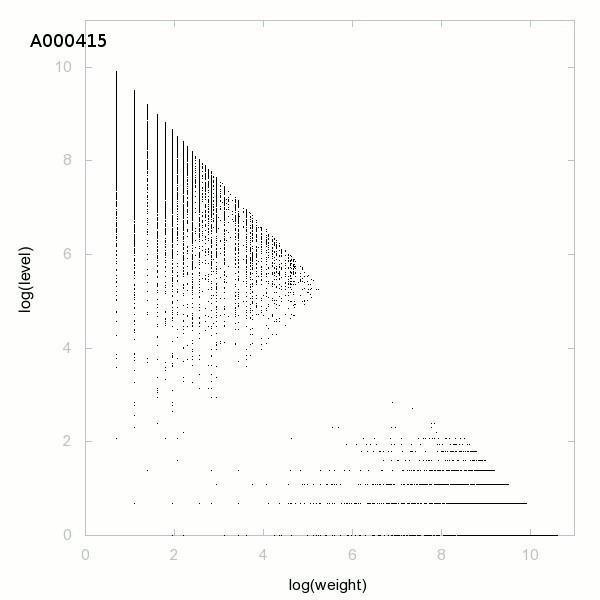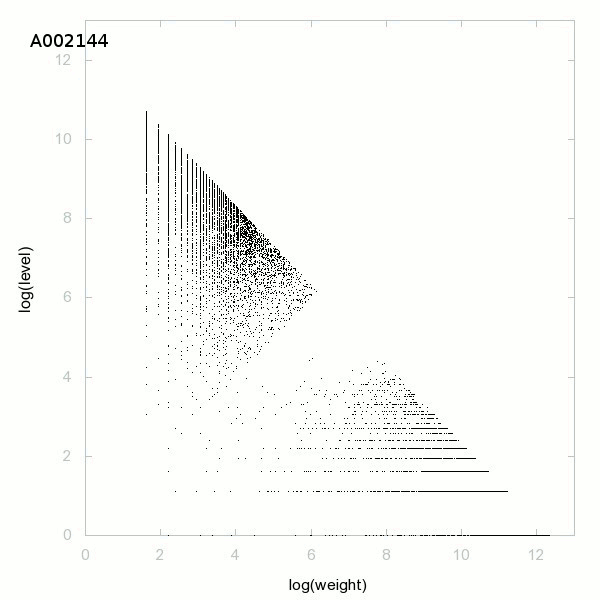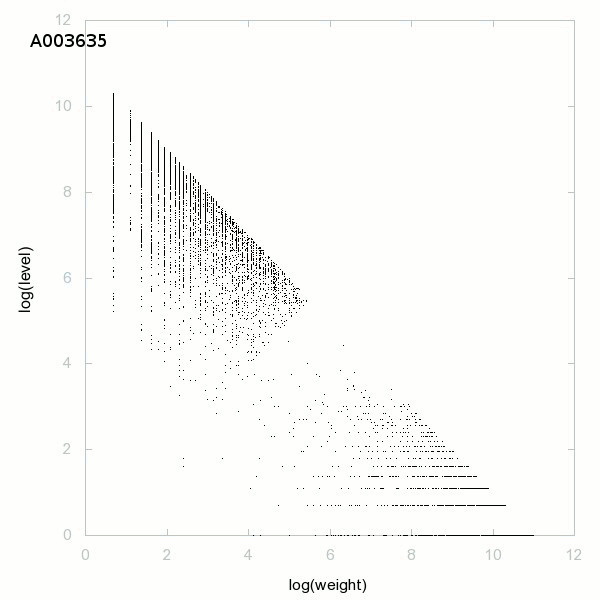
Edit 12/08/2021 : correction des liens des images, le forum ne suit plus les redirections. -
.
Edit : le message est difficile à assumer, je l'ai supprimé et remis.
Edit 2 : en fait je n'assume pas même si c'est vrai. -
Peux-tu énoncer clairement ce théorème ?
Est-ce à nouveau cette histoire de « sauts », « poids » et « niveau » ? -
Tout nombre $a(n)$ peut se décomposer de manière unique en poids × niveau + saut si $a(n + 1) < 3/2 \times a(n)$, on a alors : le poids est le plus petit tel que dans la division euclidienne d'un nombre par son poids, le reste est le saut (première différence, écart). Le quotient est le niveau.
edit : unique -
Juste une petite question, hors-sujet :
Dis, R.E., comment as-tu fait pour publier un article sur Arxiv, sans être rattaché à un laboratoire ou sans avoir de statut particulier ? -
J'ai trouvé un garant, "endorser" en anglais, un directeur de recherche du CNRS qui a été intéressé par mon travail.
-
C'est un théorème ? ou c'est simplement des noms différents que tu donnes à 3 truc parfaitement connus (quotient, reste et dividende) ?Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin
-
Bonsoir,
Tant que ton théorème ne s'applique dans des résultats plus intéressants, ça restera sans importance. C'est à toi de prouver son intérêt par des exemples. -
lourrran : oui la décomposition en poids × niveau + saut se base entièrement sur la division euclidienne mais est aussi complètement originale et n'est pas "des noms différents que je donne à 3 truc parfaitement connus". Le poids est aussi fondamental que la première différence.
Concernant le TFA, c'est un cas limite de la décomposition : la décomposition des entiers naturels en poids × niveau + saut qui peut se résumer à la décomposition de $l(n)=n-1$ en poids × niveau.
L2M : je n'ai pas la prétention de croire que je pourrais prouver des choses intéressantes en l'état actuel. Il faudrait que je reprenne de longues études or je suis dans une petite ville, je n'ai pas les moyens financiers et j'ai un travail à plein temps que je peux difficilement quitter. De plus j'ai la certitude que des personnes bien plus compétentes que moi travaillent dessus. Ce que j'aimerais c'est avoir des échanges sur le sujet, une collaboration c'est pourquoi j'ai mis mon travail sur des wikis.
Edit : je n'ai rien prouvé d'important mais j'ai montré la relation entre cette décomposition et le TFA, créé une nouvelle classification des nombres premiers, reformulé et généralisé la conjecture des nombres premiers jumeaux et énoncé une conjecture que je pense importante (celle de ce fil). Ça devrait interpeler, non ? -
J'ai fait juste un petit essai en suivant ta définition du tout 1er message
a(n) une suite croissante d'entiers : {1,3,7,11,16,17}
a(n) :.. 1...3...7...11....16.....17
d(n) :...2..4...4....5......1
l(n)..: ..0...0...0....6......15
k(n) :...0...0...0....6.......3
L(n) :...0...0...0....1.......5
Et maintenant ? -
Seuls 11 et 16 sont décomposables :
11 = 6 × 1 + 5
16 = 3 × 5 + 1 -
Reprenons :
Conjecture : les nombres premiers classés par niveau se raréfient parmi les nombres premiers.
Ca veut dire quoi ?
Pour chaque nombre premier, on sait définir son niveau : sauf erreur de ma part, le niveau de tous les nombres premiers vaut 1. Je me trompe ?
Probablement, parce que, si c'est le cas, la conjecture ne veut rien dire.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Parmi les entiers naturels, les nombres de niveau 1 sont les premiers+1 et si on considère la décomposition en poids × niveau de $l(n)$ alors oui les nombres premiers sont de niveau 1 :
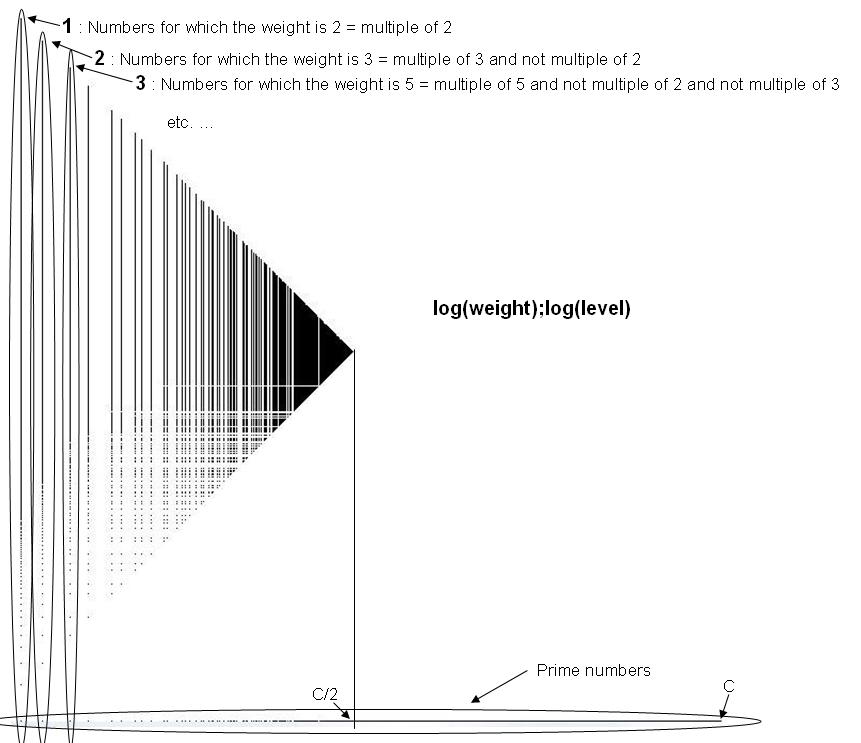
Parmi les nombres premiers, ceux-ci sont soit classés par poids soit par niveau :
Et ce sont les nombres premiers classés par niveau qui se raréfient parmi les nombres premiers.
Les nombres premiers classés par poids : https://oeis.org/A162175
Les nombres premiers classés par niveau : https://oeis.org/A162174 -
Ce que j'aimerais bien comprendre, c'est comment tu choisis tes suites a (n) ? Au hasard ?
-
Sur la base de tes messages, je ne comprenais strictment rien. C'est inquiétant. Et en cliquant sur les 2 liens vers oeis.org, j'ai enfin compris ce que tu essayais de nous expliquer.
Ce qui tendrait à prouver que je comprends mieux l'anglais que le français.
Ou pas.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
nodgim : tout a commencé avec A117078, les poids des nombres premiers, le première suite que j'ai donc décomposée et la suite des nombres premiers. Ensuite j'ai décomposé les entiers naturels puis la dizaine de suites qui sont dans les wikis. Sur mon site il y a 1000 suites décomposées, il me fallait des suites strictement croissantes, avec une croissance pas trop grande et idéalement avec un b-file de 10000 termes. J'ai commencé par les "nice" et j'ai continué un peu au hasard.
lourran : il me semble que les principes de décomposition et de classifications sont bien expliqués dans mon preprint et dans les wikis (oeiswiki et wikiversité). Il me semble aussi que mon premier message est clair. Mais si tu pouvais être plus précis et dire où sont tes problèmes de compréhension, ça serait plus constructif pour l'échange. En tout cas c'est beaucoup mieux que d'être ignoré. -
Je commence à comprendre...
Une chose tout de même me chagrine d'abord dans ta réponse à l'exemple que j'avais donné : pourquoi as-tu écrit 16 = 3 * 5 + 1 ? Dans le tableau, je ne vois pas la décomposition de 15, seulement 16 = 15 * 1 + 1.
Sinon, j'ai compris que si on utilise la suite des entiers naturels, on extrait bien les nombres premiers classés par leur niveau ( = 1) . On remarque au passage que d(n) n'a pas beaucoup d'utilité, étant toujours égal à 1. Je remarque également que pour trouver le k(n) d'un grand nombre impair (+1), il faut bien tenter de le décomposer pour trouver son plus petit diviseur. C'est facile pour les petits nombres, mais pour les grands nombres ? Donc, ça ne fait pas beaucoup avancer la connaissance des nombres premiers.
En revanche, là où on peut éventuellement s'amuser, c'est sur le k(n). Mais bon, là encore, il y a ce décalage dû à d(n) = 1, et ma foi, on peut autant s'amuser à faire la liste des plus petits diviseurs des entiers pris les uns après les autres,
mais ça c'est assez connu.
Y a-t-il d'autres suites a(n) qui te semblent avoir un intérêt ? -
$a(n)=16$ et $a(n+1)=17$ donc $d(n)=1$ et $l(n)=15$.
Le plus petit $k>1$ qui divise $15$ est $3$ et on donc bien $16 = 3 \times 5 + 1$
Effectivement pour les entiers naturels, on retombe sur le TFA et le crible d’Ératosthène. Pas de révolution ici mais c'est bien de retomber sur des choses fondamentales à partir d'une décomposition originale.
>Y a t'il d'autres suites $a(n)$ qui te semblent avoir un intérêt ?
Au hasard, les nombres premiers ? Je vais remettre encore une fois leur décomposition avec les suites de l'OEIS :
Ici, tu les as en 3D (three.js - WebGL)
Tu remarques deux nouvelles "classes" de nombres premiers (classés par poids ou par niveau), tu peux remarquer aussi que les plus petits des nombres premiers jumeaux ($>3$) ont un poids de $3$...
Merci sincèrement pour ton intérêt. -
@ RE: OK, j'avais fait une erreur dans mon tableau-exemple, j'ai corrigé.
Pour la suite des entiers naturels, j'ai donné mon avis je n'y reviens pas.
Pour la suite des nombres premiers, je vais prendre un peu plus de temps pour regarder ça.
@ + -
Bon, ben, pas grand chose à dire pour la suite des nombres premiers. Juste que le poids 3 est trivialement justifié pour les premiers jumeaux.
Désolé. -
nodgim : ne soit pas désolé, c'est bien sympa d'entretenir la conversation.
Effectivement le poids de 3 des plus petits nombres premiers jumeaux vient trivialement du fait qu'ils sont de la forme $6n-1$. D'ailleurs on peut retrouver cette forme à partir de leur décomposition en poids × niveau + saut : $3 \times L+2$ et comme le niveau est impair on retombe sur $6n-1$.
Avec la même logique, les nombres premiers qui ont un poids de 5 sont de la forme $10n-1$ (je les aime bien ceux-la : A074822).
Pour ceux ayant un poids de 7, il y a deux saut possibles (4 et 6) donc deux formes : $14n-3$ et $14n-1$.
Et ainsi de suite, on peut donc dire que c'est une classification par forme. -
Et pour répondre à la conjecture 9 proposée au tout début de ce fil : Elle n'analyse pas les nombres premiers et leur classement poids ou niveau avec une raréfaction des poids. Elle analyse les nombres p(n)-d(n), c'est à dire les nombres impairs situés aux abords des nombres premiers. Il serait tout de même extraordinaire que ces nombres p(n) - d(n) aient une caractéristique différente des autres nombres impairs voisins. La raréfaction des classés Poids provient du fait que la distance moyenne entre nombres premiers est ln(n), donc croît. Si tu regardais les autres nombres impairs voisins, tu devrais normalement tomber sur la même raréfaction.
-
Je ne comprends pas très bien ton message.
La conjecture 9 porte bien sur les nombres premiers. Je l'ai faite suivant mes données numériques et par analogie avec les entiers naturels parmi lesquels les nombres premiers se raréfient.
Sachant que par définition, les nombres premiers classés par poids suivent la conjecture de Legendre, je pense que cette conjecture est importante pour la répartition des nombres premiers. -
J'imagine que la conjecture 9 est le résultat de l'observation de la suite a(n) des nombres premiers, non ?
-
Oui bien sûr, j'ai décomposé les 150 premiers millions de nombres premiers et par analogie avec les entiers naturels.
-
Alors c'est ce que j'ai dit : tu analyses, par ton algo, la factorisation des nombres p(n)-d(n), pas les nombres premiers.
Les nombres premiers te fournissent un support des écarts, c'est tout. Pour donner un peu de corps à ce que je voudrais te faire comprendre, c'est que tu pourrais par exemple analyser les nombres p(n)-d(n)-2, et je suis certain que les résultats seront à peu près identiques. -
Quand je dis que je décompose et analyse les nombres premiers, je fais exactement ce que je dis. La suite des nombres premiers est l'entrée de l’algorithme de décomposition et je trouve aux nombres premiers décomposables leur forme en poids × niveau + saut. Après effectivement, la factorisation de $l(n)$ est centrale dans l'algorithme. Mais $l(n)=p(n)-d(n)=2p(n)-p(n+1)$ (A118534) est intimement lié aux nombres premiers (et à la suite en entrée dans le cas général).
Edit :
>tu pourrais par exemple analyser les nombres p(n)-d(n)-2, et je suis certain que les résultats seront à peu près identiques.
Je ne sais que faire de cette remarque. Comment $p(n)-d(n)-2$ vient s'insérer sans la décomposition ? De plus les diviseurs de $l(n)-2$ sont bien différents de ceux de $l(n)$. Bref cette remarque n'a pas beaucoup de sens. -
J'ai bien compris, mais si tu fais comme je te le suggères ( analyser p-d-2 par exemple) tu verras si tu as des résultats nettement différents ou à peu près équivalents. C'est seulement si tes résultats sont nettement différents que tu pourras dire que les p-d sont particuliers.
-
ah zut, j'ai fait un edit pendant que tu répondais.
Je le remets :
Je ne sais que faire de cette remarque. Comment $p(n)-d(n)-2$ vient s'insérer dans la décomposition ? De plus les diviseurs de $l(n)-2$ sont bien différents de ceux de $l(n)$. Bref cette remarque n'a pas beaucoup de sens. -
Pour préciser un peu les choses, $l(n)$ n'est pas choisi au hasard, il est imposé par la suite que l'on décompose. Et il est bien défini, je remets les définitions avec la fonction mod :
l(n) = plus grand l tel que p(n+1) = p(n) + p(n) mod l, 0 si un tel l n'existe pas ;
le poids k(n) = plus petit k tel que p(n+1) = p(n) + p(n) mod k 0 si un tel k n'existe pas ;
le niveau l(n) / k(n) si k(n) est différent de 0, 0 sinon. -
Ce que nogdim voulait dire (ce que j'ai compris), c'est :
prenons la suite des entiers premiers, on conjecture qu'elle a telle propriété : les premiers classés par niveau sont de moins en moins denses parmi les premiers.
Ça c’est ta conjecture.
Prenons une autre suite, exemple la suite $Q$ : $Q_n = P_n+2$, ou encore $Q_n =PartieEntière( P_n \times 1.15)$
Et Nogdim conjecture que ces suites ont la même propriété : plus on avance dans la suite, plus les nombres classés par niveau se raréfient.
.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
Dit comme ça, cela a plus de sens. Merci lourrran pour la reformulation.
Effectivement, je pense qu'il y a un ensemble de suites pour lesquelles cette propriété est vraie (les nombres classés par niveau se raréfient parmi les nombres de la suite). Grâce au TNP, on sait que c'est vrai pour les entiers naturels et je conjecture que c'est vrai pour les nombres premiers. Je pense que c'est vrai pour $Q_n = P_n+2$, pour la deuxième il faudrait que je me penche plus dessus.
Par contre il y a d'autres suites pour lesquelles cette propriété n'est trivialement pas vraie, par exemple les nombres k-gonaux pour lesquels tous les termes sont classés par niveau (ça doit pouvoir être prouvé facilement car les sauts ont une forme connue).
Exemple les nombres triangulaires qui ont $d(n)=n$ :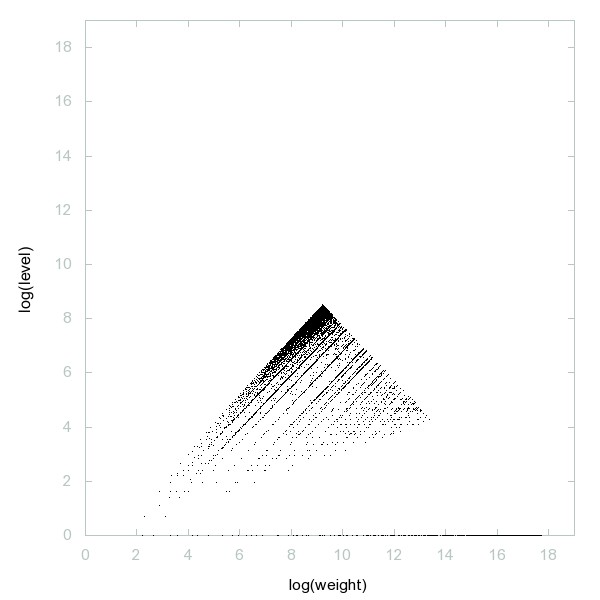
https://decompwlj.com/2Dgraph500terms/Triangular_numbers.html
Une autre suite prise un peu au hasard pour laquelle la propriété ne semble pas vraie (A000960 : Flavius Josephus's sieve: Start with the natural numbers; at the k-th sieving step, remove every (k+1)-st term of the sequence remaining after the (k-1)-st sieving step; iterate) :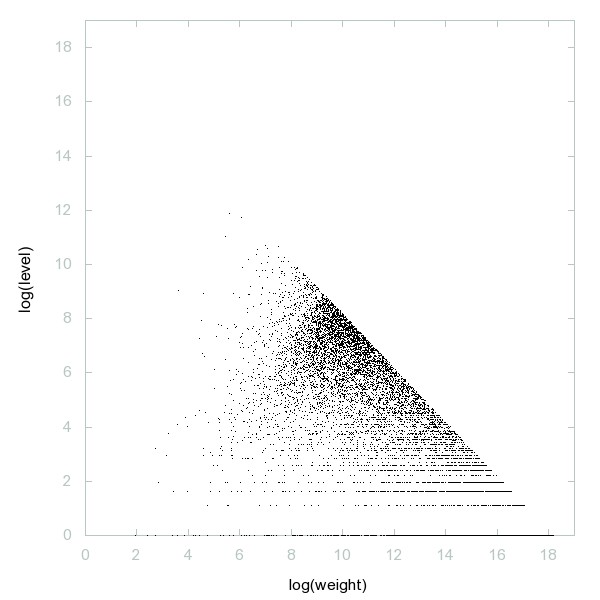
https://decompwlj.com/2Dgraph500terms/Flavius_Josephus_sieve.html
La véracité de cette propriété semble liée à la taille des sauts. De plus je pense que l'on pourrait classer les suites entre elles via cette propriété.
PS : nogdim, désolé si j'ai pu paraître un peu agressif, ce n'était pas mon intention. Ça fait plusieurs années que je n'ai pas eu un tel échange sur ma décomposition et c'est en grande partie grâce à toi. -
@ R.E. : pas de souci, je ne m'étais pas fait comprendre correctement, merci à Iourran.
OEIS contient énormément d'algorithmes. Je ne compte plus les fois où, après avoir travaillé sur un sujet qui me paraissait original, et pour lequel j'avais proposé une question, on m'a répondu que ce sujet était déjà décrit dans OEIS. Assez déprimant...
Pour intéresser ton algorithme, il faudrait que tu trouves une règle originale pour une suite donnée, que la question ait un intérêt pour une analyse poussée. J'ai donné mon avis sur la suite des nombres premiers et la suite des entiers, en disant que selon moi ça ne pouvait pas mener sur un résultat attractif. Mais bon, ça pourra peut être un jour servir, qui sait ? -
C'est une critique qui revient assez souvent : les principes de décomposition et de classification sont intéressants mais par forcément utiles. Il faudrait un gros résultat pour prouver définitivement que cela apporte quelque chose de voir les nombres de cette façon. Malheureusement je suis bien incapable de produire un tel résultat. J'aimerais vraiment que les mathématiciens du monde académique étudient ma décomposition, je suis sûr que ce ne serait pas du temps perdu.
Après je le redis mais je pense que c'est une extension du théorème fondamental de l'arithmétique et une manière originale de voir les nombres. -
(tentative de piratage de Shtam)
raoul.S, Homo Topi, Collag3n : j'aimerais bien avoir votre avis sur mon "travail" si tant est qu'un shtameur (je préfère crackpot, c'est moins blague privée) puisse faire un travail.
Parmi les autres pourfendeur de crackpot seul lourrran est intervenu mais sans vraiment donner un avis, je pense que les autres tels Fin de partie, gerard0 m'ont mis sur liste noire.
Alors c'est sûr, je n'ai pas démontré une grande conjecture, juste proposé un nouveau théorème fondamental de l’arithmétique. (il y a beaucoup d'informations sur ce fil) -
Les nombres premiers en 3D :
https://decompwlj.com/3Dgraph/Prime_numbers.html
Google dit qu'il y a 0 backlink vers cette page, lol. -
@R.E Je ne travaille ni dans le milieu universitaire ni dans l'enseignement donc mon avis n'a aucun weight (:P). Et de toute façon je n'ai pas les connaissances suffisantes en théorie des nombres pour pouvoir me prononcer sur l'intérêt de ta décomposition.
Ceci dit je pense que tu n'es pas un shtameur mais un amateur, car le vrai shtameur ne comprend pas ce qu'il écrit...
PS. si ça intéresse quelqu'un voici l'article de R.E https://arxiv.org/pdf/0711.0865.pdf. -
Et du coup, comme il comprend ce qu'il écrit, c'est beaucoup moins intéressant.Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin
-
lourrran : c'est beaucoup moins intéressant
Je dirais surtout que c'est beaucoup moins amusant pour vous. Après je comprends, il est plus aisé de critiquer ou d'attaquer une preuve foireuse d'une grande conjecture que mon travail. Vous demandez du sérieux aux shtameurs, amateurs, crackpots (appelez-les comme vous voulez) et quand on vous présente quelque chose d'à peu près sérieux, il n'y a plus personne. C'est la facilité et dans votre cas, je ferais sûrement de même. Mais de mon côté, c'est rageant et frustrant et je ressens une profonde injustice. Depuis 14 ans, je pense tous les jours à ma décomposition et je n'ai personne à qui en parler dans mon entourage ou sur internet, c'est même devenu un secret honteux. Je donnerais cher pour avoir un échange sérieux sur ma décomposition.
Bonne journée -
Pas la peine de me demander mon avis, j'ai trop la flemme de lire.
-
Bonjour RE.
Ce qui est surprenant, c'est qu'en 14 ans tu ne te sois jamais posé la question de l'utilité de ta conjecture. Si personne ne la reprend ni ne la critique, c'est qu'elle n'intéresse pas.
Tu as eu une idée, c'est bien. Tu l'exposes, elle n'intéresse personne. Soit tu peux en déduire des résultats utiles, tu les présentes, et ça va commencer à intéresser ; soit tu restes sur "j'ai eu une idée" et ça ne sert à rein de revenir en parler. Des tas de gens ont des idées, la plupart n'en font pas tout un plat.
Et tu te ridiculises en écrivant "je n'ai pas démontré une grande conjecture, juste proposé un nouveau théorème fondamental de l’arithmétique".
14 ans sur une petite idée qui n'aboutit à rien, on appelle ça de la monomanie. Désolé. -
Tu as défini le niveau d'un nombre premier par une certaine formule.
Pour information, cette définition de niveau d'un nombre premier, c'est une invention à toi, où c'est un outil classique ?
Je pose cette question, parce que cette définition me paraît extrêmement artificielle. (et donc sans intérêt, disons-le).
Tu dis ensuite que 'Plus on travaille sur des nombres grands', plus ce niveau devient 'globalement' grand.
Oui, bien évidemment. Où est la surprise ?Tu me dis, j'oublie. Tu m'enseignes, je me souviens. Tu m'impliques, j'apprends. Benjamin Franklin -
J'ai défini le niveau de beaucoup de nombres pas que des nombres premiers et oui la décomposition en poids × niveau + saut est une invention à moi :
(avec la fonction mod)
l(n) = plus grand l tel que p(n+1) = p(n) + p(n) mod l, 0 si un tel l n'existe pas ;
le poids k(n) = plus petit k tel que p(n+1) = p(n) + p(n) mod k 0 si un tel k n'existe pas ;
le niveau l(n) / k(n) si k(n) est différent de 0, 0 sinon.
Et non, je ne trouve pas ça artificiel.
>Tu dis ensuite que 'Plus on travaille sur des nombres grands', plus ce niveau devient 'globalement' grand.
Où ai-je dis ça ? Le niveau possible d'un nombre augmente avec sa taille mais il peut être aussi de niveau 1 même très grand.
Je n'ai pas bien compris, je pense. -
Ah zut, j'avais loupé la réponse de gerard0.
La décomposition en poids × niveau + saut des entiers naturels se résume au théorème fondamental de l'arithmétique et je l'applique sur 1000 suites. C'est donc bien une généralisation du ce théorème ou un nouveau théorème fondamental de l'arithmétique.
Effectivement si tout le monde s'en foutait, je pense que je serais passé à autre chose mais je suis persuadé (sans preuve) que des entités s'intéressent à ma décomposition et je pense que le monde académique à 8 ans de retard.
Alors oui, je suis monomaniaque, oui j'ai une santé mentale fragile, (j'ai quand même un travail à plein temps ou je trouve de la reconnaissance) mais je pense que cette invention vaut le coup.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres




