Lecture zen
Nous expliquons ici comment rédiger un article pour le site.
Guide pour les auteures et auteurs
Nous expliquons ici comment rédiger un article pour le site.
Introduction
Vous souhaitez écrire un cours, un article ou un exercice sur le site. Nous vous expliquons ici comment faire.
Voici tout d’abord les liens :
Votre texte sera rédigé en LaTeX. Vous pouvez utiliser des environnements ou des macros personnelles. Votre texte pourra contenir des images (via la commande
includegraphics), des figures pstricks, tikz ou picture.Il faut comprendre avant tout qu’un rendu complet et parfait du LaTeX dans un navigateur internet est difficile. En effet, LaTeX est un langage sophistiqué de part la variété des packages qu’il permet d’utiliser et il n’est possible que d’en restituer une version simplifiée.
Principe général d’édition des documents
Structure générale d’un document LaTeXsur le site
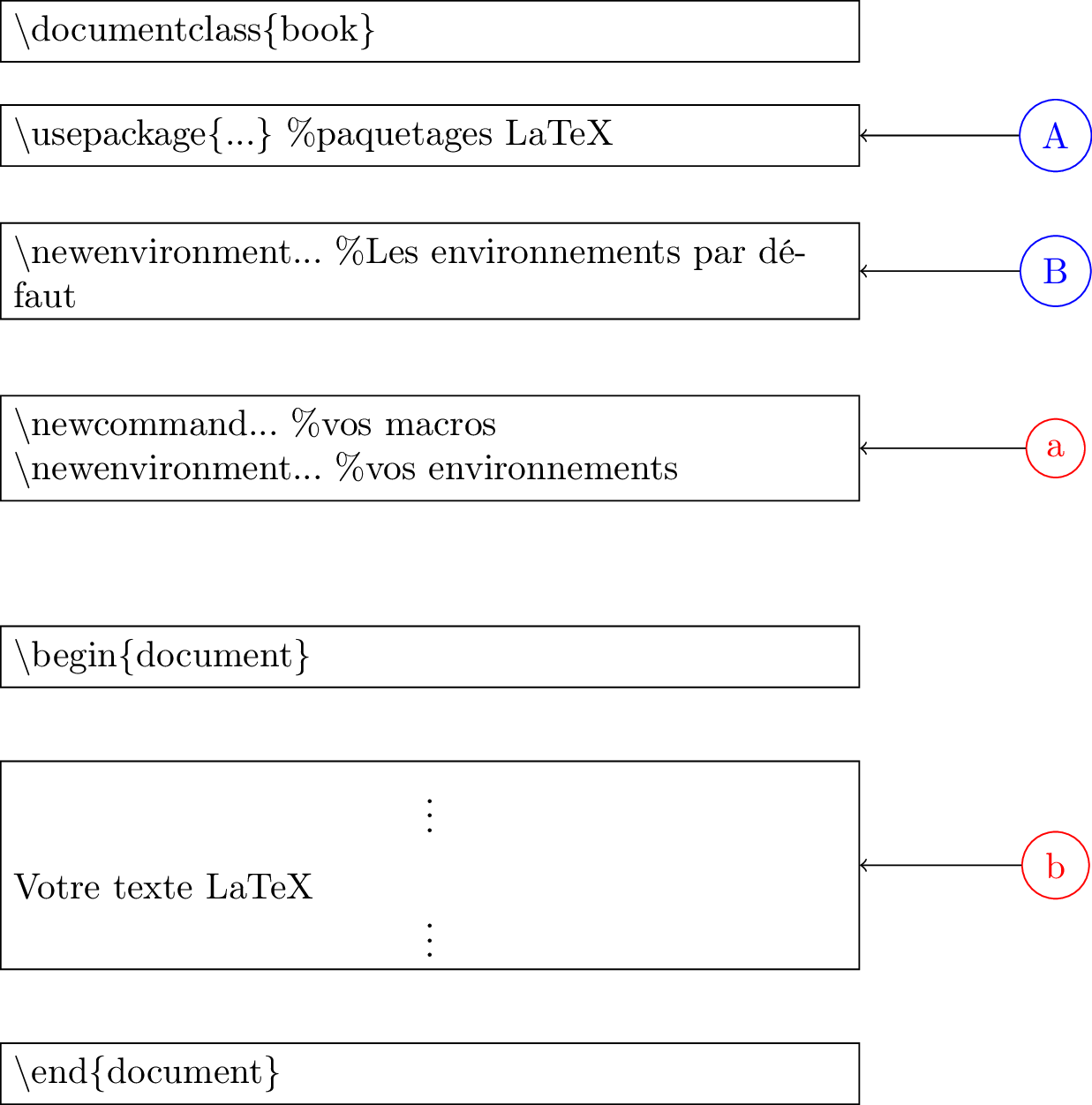
Voici la structure générale d’un document LaTeXtel qu’il sera compilé sue le site:
Les parties \((A)\) et \((B)\) sont fixes et contiennent les champs suivants :
Pour \((A)\) :%% Packages Additionnels \usepackage{float} \usepackage{amsmath} \usepackage{amsfonts} \usepackage{graphicx} \usepackage{textcomp} \usepackage{amssymb} \usepackage{bmpsize} \usepackage[utf8]{inputenc} \usepackage[T1]{fontenc} \usepackage[french]{babel} \usepackage[all]{xy} \usepackage{xcolor} \usepackage{color,colortbl} %\usepackage{caption} %\usepackage{subcaption} %\captionsetup{compatibility=false} \usepackage{wrapfig} \usepackage{multicol} \usepackage{mathtools} \usepackage{enumitem} \usepackage{framed} \usepackage[framed,amsmath,thref]{ntheorem} \usepackage{thmtools} \usepackage{etoolbox} \usepackage{fancybox} \usepackage{ifthen} \usepackage{animate} \usepackage{stmaryrd} \usepackage{mathrsfs} \usepackage{fancyvrb} \usepackage{pifont} \usepackage{multirow} \usepackage{array} \usepackage{longtable} \usepackage{booktabs} \usepackage{authblk} \usepackage{listings} \usepackage{extarrows} \usepackage{tikz} \usepackage{tkz-tab} \usepgflibrary{arrows} \usetikzlibrary{arrows,calc,shapes,chains,scopes,3d,decorations.markings,intersections,mindmap,petri,topaths} \usetikzlibrary{decorations.pathmorphing, backgrounds, positioning, fit, shapes.geometric,fit,quotes,angles} \usepackage{tikz-3dplot} \usepackage{auto-pst-pdf} \usepackage{pst-all} \usepackage{pst-3d} \usepackage{pst-text} \usepackage{pst-plot} \usepackage{pst-solides3d} \usepackage{pst-3dplot,pst-fractal} \usepackage{multido} \usepackage{fp} \usepackage[french]{varioref} \usepackage{hyperref} \usepackage{amscd} \usepackage{tabvar} \usepackage{verbatim,etoolbox} \lstset{ language=bash, %% PHP, C, Java, etc... bash is the standard extendedchars=true, inputencoding=latin1 }
Pour \((B)\) :\newenvironment{theoreme}[2][0]{#1 #2}{} \newenvironment{theorem}[2][0]{#1 #2}{} \newenvironment{proposition}[2][0]{#1 #2}{} \newenvironment{propriete}[2][0]{#1 #2}{} \newenvironment{lemma}[2][0]{#1 #2}{} \newenvironment{lemme}[2][0]{#1 #2}{} \newenvironment{definition}[2][0]{#1 #2}{} \newenvironment{defprop}[2][0]{#1 #2}{} \newenvironment{proof}[2][0]{#1 #2}{} \newenvironment{preuve}[2][0]{#1 #2}{} \newenvironment{demonstration}[2][0]{#1 #2}{} \newenvironment{exemple}[2][0]{#1 #2}{} \newenvironment{notation}[2][0]{#1 #2}{} \newenvironment{application}[2][0]{#1 #2}{} \newenvironment{remark}[2][0]{#1 #2}{} \newenvironment{remarque}[2][0]{#1 #2}{} \newenvironment{attention}[2][0]{#1 #2}{} \newenvironment{planpreuve}[2][0]{#1 #2}{} \newenvironment{exercice}[2][0]{#1 #2}{} \newenvironment{solution}[2][0]{#1 #2}{} \newenvironment{explication}[2][0]{#1 #2}{} \newenvironment{corollaire}[2][0]{#1 #2}{} \newenvironment{corollary}[2][0]{#1 #2}{} \newenvironment{programmeMP}[2][0]{#1 #2}{} \newenvironment{PlusLoin}{}{} \newenvironment{Chapeau}{}{} \newenvironment{ImageChapeau}{}{} \newenvironment{maple}[1]{#1}{} \newenvironment{python}[1]{#1}{} \newenvironment{algo}[2][0]{#1 #2}{} \newenvironment{indic}[2][0]{#1 #2}{} \newenvironment{indication}[2][0]{#1 #2}{} \newenvironment{listeronde}{\begin{enumerate}}{\end{enumerate}} \newenvironment{hypothese}{\begin{enumerate}}{\end{enumerate}} \renewenvironment{multicols}[1]{}{} \newenvironment{etapeplan}[2][0]{#1 #2}{}
La liste des paquetages sera amenée à évoluer, n’hésitez pas à proposer des paquetages supplémenentaires si besoin.
Ce que vous devez renseigner
Vous pouvez intervenir sur les champs \((a)\) et \((b)\).
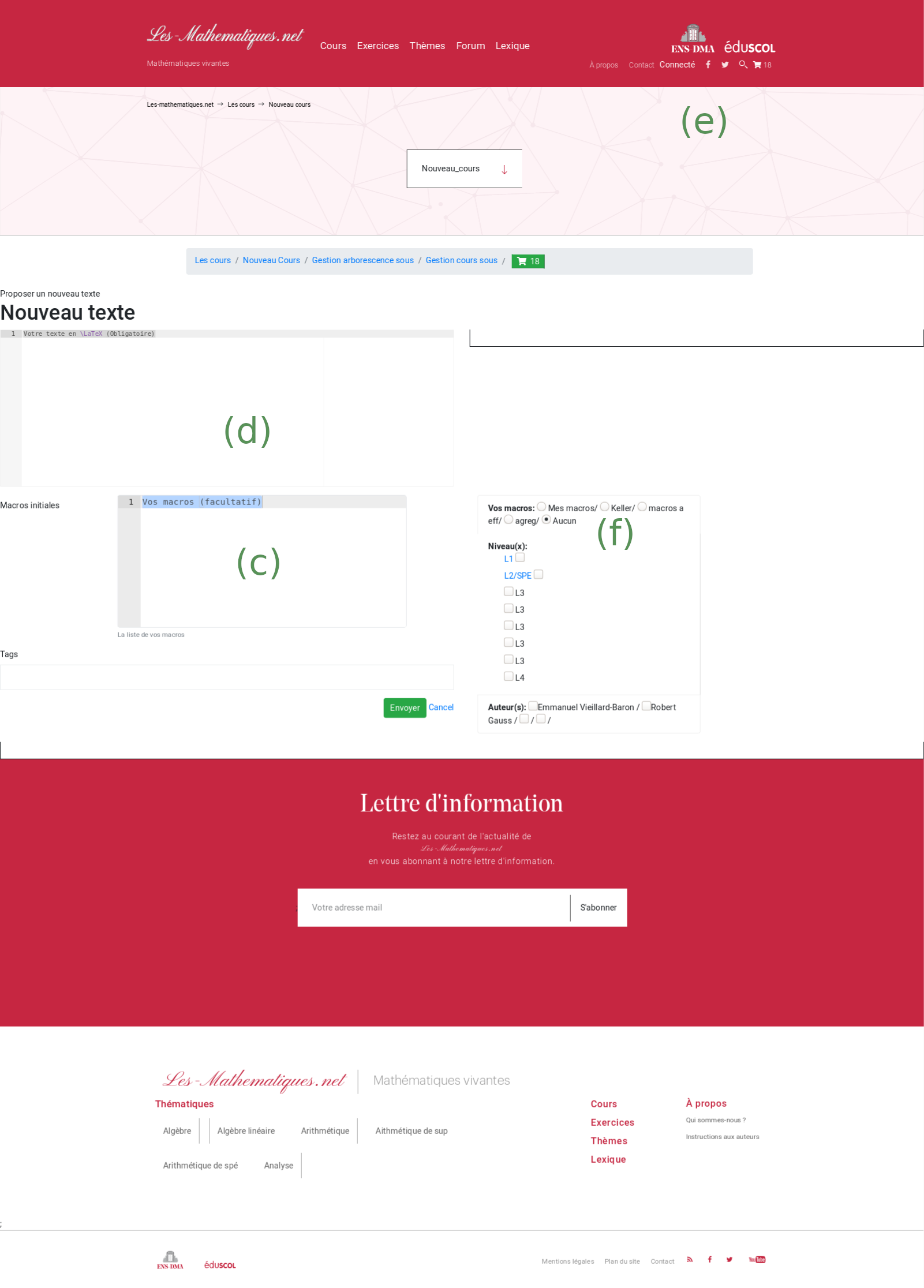
La partie \((a)\) correspond à votre jeu de macros et d’environnements. On peut suivre deux méthodes pour le renseigner:
soit vous ajoutez ces données directement dans l’interface de saisie du texte dans la zone \((c)\) du shéma ci-dessous.
soit vous pré-saisissez votre jeu de commandes dansConnecté>Mes MacrosLaTeX puis sélectionner ce jeu de macros au moment de la saisie du texte (c’est-à-dire les zones \((e)\) et \((f)\) du schéma ci-dessous).
Notons que ces deux méthodes peuvent être utiliser conjointement.
La partie \((b)\) de votre document LaTeX, c’est-à-dire tout votre texte se trouvant entre les balises\begin{document}et\end{document}est à saisir dans le champs de formulaire \((d)\) du schéma ci-dessous.
Macros et paquetages par défaut, fichier gabarit
La liste des paquetages \((A)\) que nous utilisons et celle des environnements par défaut \((B)\) a été précisée ci-dessus.
Afin de réaliser des tests sur votre machine, vous pouvez télécharger un gabarit LaTeXà cette adresse: Gabarit LaTeX.
Avant de saisir un texte sur le site, Nous vous conseillons de tester votre document en le compilant sur votre machine et en utilisant ce fichier gabarit.
Problèmes de compilation
Si vous ne parvenez pas à compiler votre texte, la lecture des messages d’erreur suffit en général pour localiser l’origine du problème.
Si ce n’est pas le cas, n’hésitez pas à utiliser le gabarit mentionné dans la sous-section précédente.
Si vous parvenez à compiler votre texte sur votre machine avec ce gabarit et que le problème persiste sur le site, n’hésitez pas à nous contacter.
Les trois grands modes de saisie
Saisie d’un cours ou d’un article
Tout se passe aux deux adresses suivantes: Voici tout d’abord les liens :
La sous-section précédente traitait du principe général d’édition sur le site. Nous nous intéressons maintenant à la structuration de votre texte c’est-à-dire la partie se trouvant entre les balises
\begin{document} et \end{document}.Afin d’obtenir le meilleur rendu possible, il est conseillé de respecter la structure suivante pour la partie \((d)\) de votre texte (mais ce n’est pas obligatoire) :
\chapter{Le titre} %Pour l'affichage du titre de l'article
\begin{ImageChapeau}{ }
\includegraphics[scale=1]{/.../image.png} %Pour l'image en haut de page
\end{ImageChapeau}
\begin{Chapeau}{ }
Le texte du chapeau %Pour le texte de presentation
\end{Chapeau}
\section{Titre premiere section}
texte...Voici un exemple de texte rédigé en utilisant cette structure et en respectant les environnements prédéfinis du site. Plus vous collerez à cette structure, mieux votre texte sera présenté:
\chapter{Espaces préhilbertiens}
\begin{ImageChapeau}{ }
\includegraphics[scale=1]{Schwarz.jpeg}
\end{ImageChapeau}
\begin{Chapeau}{ }
Dans tout ce chapitre, $E$ désigne un \Rev. Les sections \ref{section_def_et_regles_de_calcul}, \ref{section_orthogonalite},\ref{section_espaces_euclidiens} et \ref{section_projecteurs_et_symetries_orthogonaux} sont des rappels de première année.
On va généraliser dans ce chapitre la notion de produit scalaire étudiée dans
les chapitres de géométrie plane et dans l'espace aux espaces vectoriels. Cela
permettra d'étendre la notion de vecteurs orthogonaux et les notions afférentes
(norme, base orthonormale, théorème de Pythagore, projections et symétries
orthogonales...) à certains espaces vectoriels de fonctions ou de matrices par
exemple. Un des prolongements importants de ce chapitre sera celui consacré
aux séries de
Fourier en seconde année et qui formera un magnifique exemple d'illustration de
la puissance de l'algèbre mise au service de l'analyse.
Nous étudierons dans la seconde moitié de ce chapitre les endomorphismes d'un
espace euclidien qui préservent le produit scalaire, ou autrement dit les
isométries. Nous verrons que les isométries d'un espace euclidien $E$ donné
forment un groupe appelé groupe orthogonal et nous étudierons complètement ce
groupe dans le cas o\`{u} $E=\R^2$ et $E=\R^3$. Nous ferons le lien entre les
matrices et ces endomorphismes remarquables et nous introduirons
la notion de matrice orthogonale.
\end{Chapeau}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\section{Définitions et règles de calcul}\label{section_def_et_regles_de_calcul}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\subsection{Produit scalaire}
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\begin{definition}[3]{Produit scalaire}\index{Produit_scalaire@Produit scalaire}
Soit $E$ un $\R$-espace vectoriel. On appelle \emph{produit scalaire} sur
$E$,
une application~: $\phi: E\times E \rightarrow \R $ vérifiant~:
\begin{listeronde}{ }
\item $\phi$ est une \emph{forme bilinéaire} : $\forall (x,y,z)\in
E^3, \forall (\lambda,\mu)\in \R^{2}$
\begin{align*}
\phi(\lambda x +\mu y, z) &= \lambda \phi(x,z) + \mu \phi(y,z) ,\
\phi(x,\lambda y + \mu z ) & = \lambda \phi(x,y) + \mu \phi(y,z).
\end{align*}
\item $\phi$ est {\emph{symétrique}} :
$$
\forall (x,y)\in E^2, \SP \phi(x,y)= \phi(y,x). $$
\item $\phi$ est {\emph{définie}} :
$$
\forall x\in E, \SP (\phi(x,x)=0)\equivaut (x=0). $$
\item $\phi$ est {\emph{positive}} :
$$
\forall x \in E, \SP \phi(x,x)\geq 0. $$
\end{listeronde}
\end{definition}
...
\begin{theoreme}[1]{Théorème de Schmidt}
\index{Theoreme@Théorème!de Schmidt}
\index{Orthogonalite@Orthogonalité!Schmidt}
\index{Algorithme@Algorithme!de Schmidt}\label{Procede_orthonomalisation_Schmidt}
Soit $E$ un espace euclidien et $e=(e_1,\dots,e_n)$ une famille libre de
$E$. Alors il existe \fbox{\emph{une et une seule famille orthonormale}}
$\epsilon=(\epsilon_1,\dots,\epsilon_n)$ de $E$
vérifiant :
\begin{multicols}{2}
\begin{listeronde}{ }
\item $\forall i\in \interventier{1}{n}, \quad \vect(\epsilon_1,\dots,\epsilon_i) =
\vect(e_1,\dots,e_i)$ ;
\item $\forall i\in \interventier{1}{n}, \quad \scal{e_i}{\epsilon_i} > 0$.
\end{listeronde}
\end{multicols}
\end{theoreme}
\begin{figure}[htbp]
\centering
\begin{pspicture}(-1.5,-1.5)(2,2)
%vecteurs \eps_1,2,3
\psline[linecolor=blue,linewidth=2pt]{->}(0,0)(-0.5,-0.5)
\uput[0](-0.5,-0.5){$\color{blue} \vecteur{\eps_1}$}
\psline[linecolor=blue,linewidth=2pt]{->}(0,0)(1,0)
\uput[-90](1,0){$\color{blue} \vecteur{\eps_2}$}
%vecteurs e_1, e_2, e_3
\psline[linecolor=blue,linestyle=dashed]{->}(0,0)(-1,-1)
\uput[0](-1,-1){$\color{blue} \vecteur{e_1}$}
\psline[linecolor=blue,linestyle=dashed]{->}(0,0)(0.5,-0.5)
\uput[-90](0.5,-0.5){$\color{blue} \vecteur{e_2}$}
%vecteur e3
\psline[linecolor=red,linewidth=2pt]{->}(0,0)(2,1)
\uput[0](2,1){$\color{magenta} \vecteur{e_3}$}
\psline[linecolor=magenta,linestyle=dashed]{<-}(0,1.5)(2,1)
\uput[90](1.2,1.4){
$\color{magenta} \lambda \vecteur{\eps_1} + \mu \vecteur{\eps_2}$}
\psline[linecolor=red,linewidth=2pt]{->}(0,0)(0,1.5)
\uput[180](0,1.5){\color{red} $\vecteur{f_3}$}
\psline[linecolor=blue,linewidth=2pt]{->}(0,0)(0,1)
\uput[180](0,1){$\color{blue} \vecteur{\eps_3}$}
\end{pspicture}
\caption{Algorithme de Schmidt~: redressement de $e_3$}
\label{fig:redressement_schmidt}
\end{figure}
\begin{preuve}{ }
La preuve est constructive et par récurrence sur la taille $n$ de la famille libre $e$.
\begin{itemize}
\item[$\bullet$] \fbox{Initialisation}~: La famille $e=(e_1)$ est libre par hypothèse et donc $e_1$ est non nul. Le vecteur $\epsilon_1=\dfrac{e_1}{ \norme{e_1}}$ est alors le seul vecteur unitaire de $E$ vérifiant que $\Vect\p{\e_1}= \Vect\p{\epsilon_1}$ ainsi que
$\scal{e_1}{\epsilon_1}=\norme{e_1}>0$.
\item[$\bullet$] \fbox{Hérédité} Soit $k\in \intere{1}{n-1}$. Supposons construite la famille $(\epsilon_1,\hdots,\epsilon_k)$ répondant à l'énoncé.
Construisons un vecteur $\epsilon_{k+1}$
répondant au problème. Comme $\eps_{k+1}\in\Vect(e_1,\hdots,e_k,e_{k+1})=\Vect(\eps_1,\hdots,\eps_k,e_{k+1})$ (voir la figure
\ref{fig:redressement_schmidt}), on cherche $\eps_{k+1}$ sous la forme $\epsilon_{k+1}=\lambda\p{e_{k+1} -\alpha_1 \epsilon_1-\hdots-\alpha_k \epsilon_k } $ o\`{u}~:
pour tout $ i\in\intere{1}{k},\quad \alpha_i\in\R$ et o\`{u} $\lambda\in\R$.
La condition d'orthogonalité de la famille est équivalente à, pour tout $i\in\intere{1}{k}$~:
$$\scal{\eps_{i}}{\eps_{k+1}}=0=\lambda\p{\scal{\eps_i}{e_{k+1}} -\alpha_i\scal{\eps_i}{\eps_i}} $$, c'est-à-dire $\alpha_i=\scal{\eps_i}{e_{k+1}}$.
La constante $\lambda$ est strictement positive. En effet~:
$$\lambda\scal{e_{k+1}}{\eps_{k+1}}=\scal{\eps_{k+1}+\lambda\serie{i=1}{k} \alpha_i \eps_i}{\eps_{k+1}}=\norme{\eps_{k+1}}^2 $$ et est donc entièrement déterminée par le fait que $\eps_{k+1}$ est unitaire.
On obtient ainsi un unique vecteur $\eps_{k+1}$ satisfaisant l'énoncé. Il est donné par $$\eps_{k+1}=\dfrac{\tilde\eps_{k+1}}{\norme{\tilde\eps_{k+1}}} \text{ o\`{u} } \tilde\eps_{k+1}=e_{k+1}-\serie{i=1}{k}\scal{\eps_{i}}{e_{k+1}}\eps_i.$$
\end{itemize}
\end{preuve}
...et voici son rendu avec le jeu de macros approprié :
Saisie d’un exercice
Rendez vous à l’adresse suivante pour saisir un nouvel exercice
Vous pouvez saisir brutalement votre exercice sans vous préoccuper du chapeau ou du titre.
Il y a deux méthodes pour saisir un exercice avec solution:
soit vous rendre sur la page de l’exercice et poster votre solution à ce niveau
soit saisir en bloc l’exercice avec la solution en utilisant la méthode de ’saisie d’un fichier d’exercice ci-dessous’
Saisie d’un fichier d’exercice
Vous voulez saisir une liste d’exercices avec ou sans solution, voici comment procéder:
Rendez-vous sur la page de saisie d’un fichier d’exercices
Renseignez votre liste d’exercice formate de la façon suivante :
\begin{exercice}{ }
exercice 1
\begin{solution}{ }
Solution 1
\end{solution}
\end{exercice}
\begin{exercice}{ }
exercice 2
\begin{solution}{ }
Solution 2
\end{solution}
\end{exercice}
\begin{exercice}{ }
exercice 1
\begin{solution}{ }
Solution 1
\end{solution}
\end{exercice}
\begin{exercice}[X PC 2020]{3}
exercice 3
\begin{solution}{ }
Solution 3
\end{solution}
\end{exercice}
\begin{exercice}[Un bel exercice]{2}
exercice 3
\begin{solution}{ }
Solution 3
\end{solution}
\end{exercice}
On remarquera que :
Les exercices doivent être saisis au sein de l’environmentexercice
Cet environement est paramétrisable sous la forme\begin{exercice}[Un titre(chaine de caractères)]{une difficulté (entier de 1 à 4)} \end{exercice}
Si vous saisissez un concours dans la variable titre et une filière, ces données sont reconnues par le compilateur afin de taguer l’exercice de manière adéquate. Les filières reconnues sont les suivantes :
MP,PC,PSI,PT,TSI
Licence
Master
et les concours reconnus sont :
ENS
Polytechnique
Centrales
Mines-Ponts
CCP
Universitaire
Capes
Agrégation
Le titre
Le titre s’obtient avec la commande :
\chapter{Votre titre}Le chapeau
Le chapeau est le petit texte de présentation de votre texte, il est à renseigner ainsi:
\begin{Chapeau}{ }
...
\end{Chapeau}Attention à la majuscule à Chapeau!
L’image du chapeau
L’image du chapeau est à renseigner ainsi:
\begin{ImageChapeau}{ }
\includegraphics[scale=1]{Votre_image.ext}
\end{ImageChapeau}Cette image s’affichera automatiquement en haut de la page. Attention aux majuscules!
Les sections, les footnotes, les références
Ces commandes se renseignent comme d’habitude avec LaTeX.
Les environnements
Les environnements mathématiques par défaut
les environnements usuels
Les listes
Le code informatique
Les environements ’théorème’
Les images et les diagrammes
Tikz et Pstricks
Insertions d’images: includegraphics
L’inclusion d’une image se fait comme d’habitude avec la commande
\includepgraphics{Votre_image.png}Peut importe le lien vers l’image que vous mettez dans la commande, le compilateur du site s’occupera d’en extraire le nom de l’image. Attention, suite à la compilation du texte, le site vous demandera de verser l’image sur le serveur (formulaire d’upload qui apparaît en bas du formlaire de saisie du document).
Tableaux de variation
Vous pouvez utiliser l’excellent tutoriel qui se trouve sur Culturemath: Le tutoriel
Barre utilisateur
[ID: 2] [Date de publication: 24 novembre 2020 23:03] [Catégorie(s): Articles ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Emmanuel Vieillard-Baron ]Commentaires sur le cours
Documents à télécharger
L'article complet