Application des nombres complexes à la géométrie

  1. Les exercices
  2. Vue compacte

Exercices du dossier Application des nombres complexes à la géométrie

Exercice 71 *

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Déterminer et représenter les ensembles de nombres complexes :

  1. \(E_1=\left\{z\in\mathbb{C}~|~ \bar z=z\right\}\).

  2. \(E_2=\left\{z\in\mathbb{C}~|~ \left|z\right|\leqslant 4\right\}\).

  3. \(E_3=\left\{z\in\mathbb{C}~|~ \left|z-1\right|=\left|z+1\right|\right\}\).

  4. \(E_4=\left\{z\in\mathbb{C}~|~ \left|z-1+2i\right|=1\right\}\).

  5. \(E_5=\left\{z\in\mathbb{C}~|~ \mathop{\rm Im}z=-1\right\}\)

  6. \(E_6=\left\{z\in\mathbb{C}~|~ \arg\left(z\right)=\pi/4 ~\left[\pi\right]\right\}\)

  7. \(E_7=\left\{z\in\mathbb{C}~|~ \arg\left(z\right)=\pi/3~\left[2\pi\right]\right\}\).

  8. \(E_8=\left\{z\in\mathbb{C}~|~ \arg\left(z-1\right)=\pi/6 ~\left[\pi\right]\right\}\)

  9. \(E_9=\left\{z\in\mathbb{C}~|~ \arg\left(z-1+2i\right)=\pi/2~\left[2\pi\right]\right\}\)


[ID: 41] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 71
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

Dans toute la solution, on appelle \(M\) le point d’affixe \(z\).

  1. Un complexe est égale à son conjugué si et seulement si il est réel donc \(E_1=\mathbb{R}\).

  2. On applique le cours : \(E_2\) est le disque fermé de centre \(0\) et de rayon \(4\).

  3. Si \(A\) est le point d’affixe \(-1\) et \(B\) celui d’affixe \(-1\) alors \(\left|z-1\right|=\left|z+1\right|\) si et seulement si \(d\left(M,A\right)=d\left(M,B\right)\). Donc \(M\) est un point de la médiatrice du segment \(\left[A,B\right]\) , c’est-à-dire de l’axe imaginaire, donc \(E_2=i\mathbb{R}\).

  4. D’après le cours \(E_3\) est le cercle de centre le point d’affixe \(1-2i\) et de rayon \(1\).

  5. L’ensemble \(E_5\) est constitué de la droite passant par le point d’affixe \(-i\) et parallèle à l’axe réel.

  6. L’ensemble \(E_6\) est la bissectrice principale.

  7. L’ensemble \(E_7\) est la demi-droite d’extrémité l’origine et formant un angle de \(\pi/3\) avec l’axe des abscisses.

  8. L’ensemble \(E_8\) est l’image par la translation de vecteur \(\overrightarrow{i}\) de la droite passant par l’origine et le point d’affixe \(\left(\sqrt 3 + i\right)/2\) angle de \(\pi/3\) avec l’axe des abscisses.

  9. Enfin l’ensemble \(E_9\) est l’image par la translation de vecteur \(\overrightarrow{u}\left(1-2i\right)\) de la demi droite \([Oy)\).


Exercice 1034 *

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Soient \(A\left(1+i\right)\) et \(B\left(4+3i\right)\).

  1. Trouver l’affixe du point \(C\) pour que le triangle \(ABC\) soit équilatéral direct.

  2. Trouver l’affixe des points \(D\) et \(E\) pour que le quadrilatère \(ABDE\) soit un carré direct.


[ID: 43] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 1034
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

  1. Le triangle \(ABC\) est équilatéral direct si et seulement si \(C\) est déduit de \(B\) par une rotation de centre \(A\) et d’angle \(Pi/3\) donc on doit avoir \(Z_C=e^{i\pi/3}\left(z_B-z_A\right)+z_A\). Après calcul, on trouve que l’affixe de \(C\) est \(\boxed{z_C=5/2-\sqrt 3 +\left(2+3/2\sqrt 3\right)i}\). Réciproquement, on vérifie que ce point convient.

  2. Le quadrilatère \(ABDE\) est un carré direct si et seulement si on a en même temps :

    • le point \(D\) est l’image de \(A\) par une rotation d’angle \(-\pi/2\) et de centre \(B\).

    • le point \(E\) est l’image de \(B\) par une rotation d’angle \(\pi/2\) et de centre \(A\).

    On trouve alors \(z_D=-i\left(z_A-z_B\right)+z_B\) c’est-à-dire \(\boxed{z_D=2+6i}\) et \(z_E=i\left(z_B-z_A\right)+z_A\) c’est-à-dire \(\boxed{z_E=3-2i}\). On vérifie réciproquement que ces deux points conviennent.


Exercice 325 *

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Calculer la longueur d’un côté d’un polygone régulier à \(n\) sommets inscrit dans le cercle unité.


[ID: 45] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 325
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

On calcule pour cela : \[\lvert 1-e^{{\scriptstyle 2i\pi\over\scriptstyle n}} \rvert =\left|e^{{\scriptstyle i\pi\over\scriptstyle n}} \left(e^{-{\scriptstyle i\pi\over\scriptstyle n}} - e^{{\scriptstyle i\pi\over\scriptstyle n}}\right)\right|=\boxed{2\sin{\scriptstyle\pi\over\scriptstyle n}}\]


Exercice 1025 *

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron


[ID: 47] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 1025
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

Quitte à effectuer une translation, une rotation et une homothétie, on peut supposer que l’affixe de \(T\) est \(0\), celle de \(A\) est \(-1\) et celle de \(B\), \(1\). On note \(c,r,s\) les affixes respectives de \(C\), \(R\) et \(S\). Comme \(ARC\) est isocèle et rectangle en \(R\), \(C\) est déduit de \(A\) par une rotation de centre \(C\) et d’angle \(\pi/2\). Donc \(c-r=i\left(-1-r\right)\). De même, \(B\) est déduit de \(S\) par une rotation de centre \(S\) et d’angle \(\pi/2\), donc \(1-s=i\left(c-s\right)\). On déduit de ces deux relations que \[r=\dfrac{c+i}{1-i} \quad \textrm{ et} \quad s=\dfrac{-1+ic}{i-1} .\] Il est alors clair que \(is=r\) donc \(R\) est l’image de \(S\) par une rotation de centre \(T\) et d’angle \(\pi/2\). Autrement dit, \(RST\) est rectangle et isocèle en \(T\).


Exercice 49 **

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Trouver tous les nombres complexes tel que les points \(M\), \(N\), \(P\) d’affixes respectives \(z\), \(z^2\) et \(z^4\) sont alignés.


[ID: 49] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution


Construction à la règle et au compas du pentagone régulier *

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

      1. Résoudre dans \(\mathbb{C}\) l’équation \(z^5=1\quad \left(*\right)\).

      2. Posons \(\omega=\cos\left({\scriptstyle 2\pi\over\scriptstyle 5}\right)+i\sin\left({\scriptstyle 2\pi\over\scriptstyle 5}\right)\). Montrer que l’ensemble solution de l’équation \(\left(*\right)\) est : \(\left\{1,\omega,\omega^2,\omega^3,\omega^4\right\}\).

      3. Représenter \(\left\{1,\omega,\omega^2,\omega^3,\omega^4\right\}\) dans le plan complexe.

      4. Calculer : \(1+\omega+\omega^2+\omega^3+\omega^4\).

    2. On pose \(\alpha=\omega+\omega^4\) et \(\beta=\omega^2+\omega^3\).

      1. Déduire de que \(\alpha\) et \(\beta\) sont solutions de \(Z^2+Z-1=0 \quad \left(**\right)\).

      2. Exprimer alors \(\alpha\) en fonction de \(\cos\left({\scriptstyle 2\pi\over\scriptstyle 5}\right)\) et \(\beta\) en fonction de \(\cos\left({\scriptstyle 4\pi\over\scriptstyle 5}\right)\)

    3. Résoudre l’équation \(\left(**\right)\) et en déduire une valeur exacte de \(\cos\left({\scriptstyle 2\pi\over\scriptstyle 5}\right)\).

    1. On désigne par \(A_0\), \(A_1\), \(A_2\), \(A_3\) et \(A_4\) les points d’affixe respective \(1\), \(\omega\), \(\omega^2\), \(\omega^3\) et \(\omega^4\).

      1. Par quelle transformation simple passe-t-on de \(A_0\) à \(A_1\)? puis de \(A_1\) à \(A_2\)? Généraliser ce résultat.

      2. Quelle est l’abscisse du point \(H\) intersection de la droite \(\left(A_1A_4\right)\) avec l’axe des abscisses?

    2. Soit \(\mathscr C\) le cercle de centre \(\Omega\) d’affixe \(-{\scriptstyle 1\over\scriptstyle 2}\) et passant par le point \(B\) d’affixe \(i\). On désigne par \(M\) et \(N\) les points où \(\mathscr C\) rencontre l’axe des abscisses, \(M\) ayant une abscisse positive.

      1. Prouver que \(M\) a pour affixe \(\alpha\) et que \(N\) a pour abscisse \(\beta\).

      2. Prouver que \(H\) est le milieu de \(\left[OM\right]\).

      3. Déduire de ce qui précède la construction à la règle et au compas d’un pentagone dont on connaît le centre \(O\) et un sommet \(A_0\). Effectuer cette construction en se plaçant dans un repère orthonormal direct \(\left(O,\overrightarrow{\imath},\overrightarrow{\jmath}\right)\) avec \(\overrightarrow{\imath}=\overrightarrow{O A_0}\).


[ID: 51] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Construction à la règle et au compas du pentagone régulier
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

      1. Les solutions dans \(\mathbb{C}\) de l’équation \(z^5=1\) sont les \(5\) racines cinquièmes de l’unité: \(e^{{\scriptstyle 2ik\pi\over\scriptstyle 5}},\quad k\in\llbracket 0,4\rrbracket\).

      2. Il est clair que \(\omega=\cos\left({\scriptstyle 2\pi\over\scriptstyle 5}\right)+i\sin\left({\scriptstyle 2\pi\over\scriptstyle 5}\right)=e^{{\scriptstyle 2i\pi\over\scriptstyle 5}}\). Il est aussi clair que, pour tout \(k\in\llbracket 0,4\rrbracket\), \(e^{{\scriptstyle 2ik\pi\over\scriptstyle 5}}=\omega^k\).

      3. Voir page .

      4. On reconnaît une somme géométrique de raison \(\omega\) donc : \(1+\omega+\omega^2+\omega^3+\omega^4=\left(1-w^5\right)/\left(1-\omega\right)\) mais comme \(\omega^5=1\), il vient : \(1+\omega+\omega^2+\omega^3+\omega^4=0\).

    2. Posons \(\alpha=\omega+\omega^4\) et \(\beta=\omega^2+\omega^3\).

      1. On a : \(\omega=e^{{\scriptstyle 2i\pi\over\scriptstyle 5}}\) et \(\omega^4=e^{{\scriptstyle 8i\pi\over\scriptstyle 5}}=e^{-{\scriptstyle 2i\pi\over\scriptstyle 5}}\). Il est alors clair que \(\overline w=\omega^4\). De même, \(\omega^2=e^{{\scriptstyle 4i\pi\over\scriptstyle 5}}\) et \(\omega^3=e^{{\scriptstyle 6i\pi\over\scriptstyle 5}}=e^{{\scriptstyle-4i\pi\over\scriptstyle 5}}=\overline{\omega^2}\).

      2. On a \(\alpha^2+\alpha-1=\left(\omega+\omega^4\right)^2 + \left(\omega+\omega^4\right) -1=\omega^2+2\omega^5+\omega^8+\omega+\omega^4-1=\omega^2+2+\omega^3+\omega+ \omega^4-1=1+\omega+\omega^2+\omega^3+\omega^4=0\). Donc \(\alpha\) est solution de \(Z^2+Z-1=0\). On fait de même pour \(\beta\).

      3. On a \(\alpha=\omega+\omega^4=\omega+\overline \omega = 2\cos {\scriptstyle 2\pi\over\scriptstyle 5}\) et \(\beta =\omega^2+\omega^3 = \omega^2 + \overline{\omega^2}= 2\cos\left({\scriptstyle 4\pi\over\scriptstyle 5}\right)\)

    3. Les racines de \(Z^2+Z-1\) sont \(\left(-1-\sqrt 5\right)/2\) et \(\left(-1+\sqrt 5\right)/2\). Comme \({\scriptstyle 2\pi\over\scriptstyle 5}\in\left]0,\pi/2\right[\) et que \({\scriptstyle 4\pi\over\scriptstyle 5}\in\left]\pi/2,\pi\right[\), il vient : \(\cos {\scriptstyle 2\pi\over\scriptstyle 5} =\left(-1+\sqrt 5\right)/4\) et \(\cos {\scriptstyle 4\pi\over\scriptstyle 5} =\left(-1-\sqrt 5\right)/4\).

      1. On passe de \(A_0\) à \(A_1\), puis de \(A_1\) à \(A_2\), puis de \(A_i\) à \(A_{i+1}\) par une rotation de centre \(O\) et d’angle \(2\pi/5\).

      2. L’abscisse du point \(H\) intersection de la droite \(\left(A_1A_4\right)\) est l’abscisse de \(A_1\) qui vaut \(\cos {\scriptstyle 2\pi\over\scriptstyle 5} =\left(-1+\sqrt 5\right)/4\).

      1. Par application du théorème de Pythagore dans le triangle \(\Omega O J\), on obtient que le rayon du cercle est \(\sqrt 5/2\). Donc l’affixe de \(M\) est \(-1/2+\sqrt 5/2=\alpha\) et l’affixe de \(N\) est \(-1/2-\sqrt 5/2=\beta\)

      2. L’affixe du milieu de \(\left[OM\right]\) est \(\left(0+\alpha\right)/2=(-1+\sqrt 5)/4\) ce qui correspond à l’affixe de \(H\)..

      3. Pour construire un pentagone régulier à la règle et au compas, on commence par tracer le cercle unité \(\mathscr C_{0}\) de centre \(O\) et passant par \(A_0\). On place ensuite le point \(B\) d’affixe \(i\) et le point \(\Omega\) d’affixe \(-1/2\). On trace le \(\mathscr C\) et le milieu \(\Omega\) passant par \(B\) ce qui nous permet de construire les points \(M\) et \(N\). On lève les perpendiculaires à l’axe des abscisses passant par \(M\) et \(N\). Ces perpendiculaires intersectent le cercle unité en les points \(A_1\), \(A_2\), \(A_3\) et \(A_4\).


Propriété de l’angle au centre **

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Dans le plan muni d’un repère orthonormal direct \(\left(O,\overrightarrow{\imath},\overrightarrow{\jmath}\right)\), on considère un cercle \(\mathscr C\) de centre \(\Omega\), de rayon \(R>0\) et trois points \(A,B,M\in\mathscr C\). Prouver la propriété de l’angle au centre : \[\left(\widehat{\overrightarrow{\Omega A},\overrightarrow{\Omega B}}\right)=2\left(\widehat{\overrightarrow{MA},\overrightarrow{MB}}\right) \,\left[2\pi\right]\]


[ID: 53] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution


Exercice 815 **

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

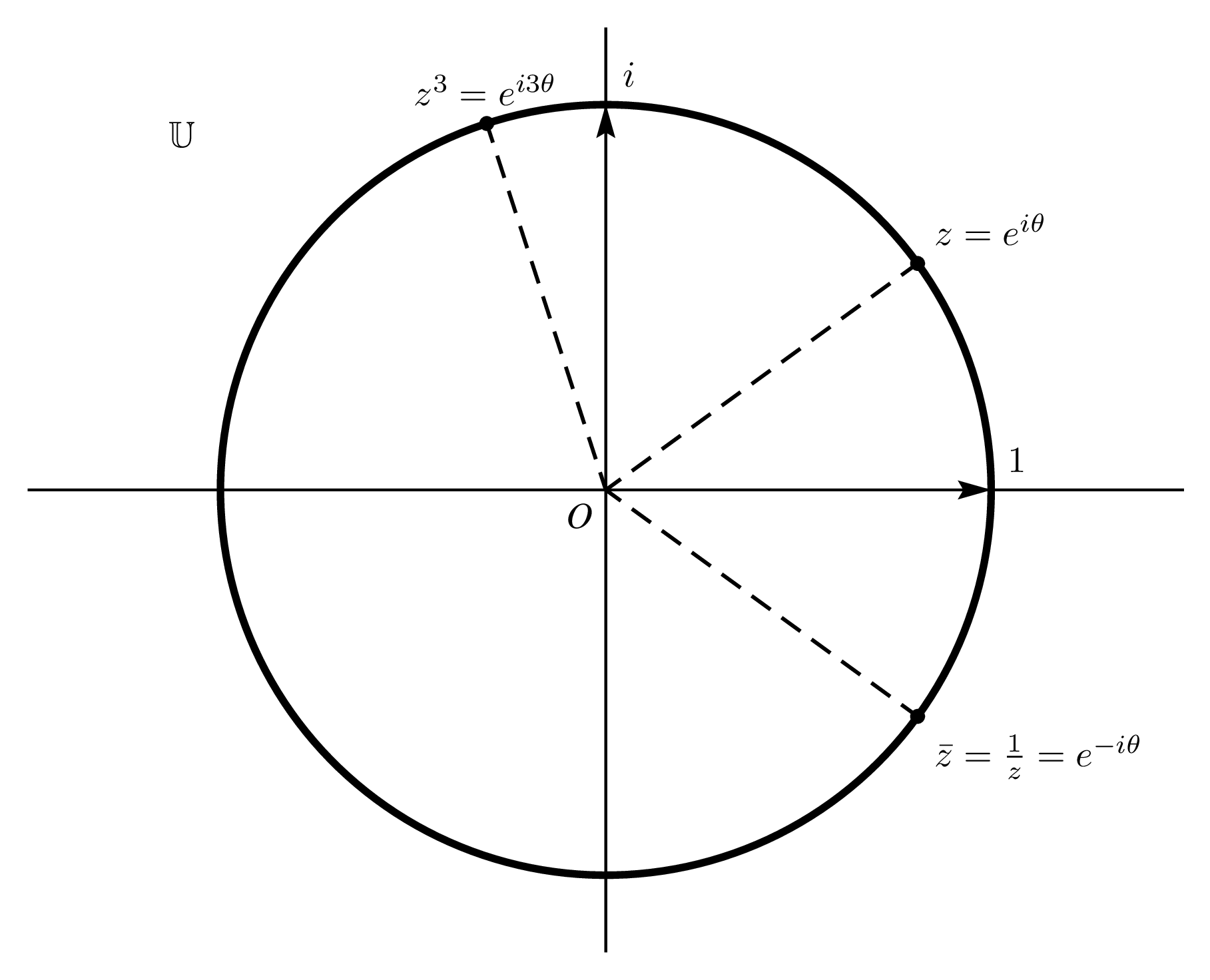
Soit \(z\in\mathbb U\setminus\left\{1\right\}\). Montrer que : \[\dfrac{z+1}{z-1}\in i\mathbb{R}.\] On pourra prouver cette propriété par trois méthodes différentes :

  1. Une méthode algébrique utilisant les propriétés du groupe \(\mathbb U\).

  2. Une méthode utilisant la factorisation par l’angle moitié.

  3. Une méthode géométrique.


[ID: 55] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 815
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

  • Comme \(z\in\mathbb U\setminus\left\{1\right\}\), on a : \(z^{-1}=\bar z\) et \[\dfrac{z+1}{z-1}=\dfrac{\left(z+1\right)\overline{\left(z-1\right)}}{\left|z-1\right|^2}= \dfrac{\bar z -z}{\left|z-1\right|^2}=-2i\dfrac{\mathop{\mathrm{Im}}(z)}{\left|z-1\right|^2}\in i\mathbb{R}.\]

  • Comme \(z\in\mathbb U\setminus\left\{1\right\}\), il existe \(\theta\in\left]0,2\pi\right[\) tel que : \(z=e^{i\theta}\). Par factorisation par l’angle moitié : \[{\scriptstyle z+1\over\scriptstyle z-1}= \dfrac{e^{i\theta}+1}{e^{i\theta}-1}=\dfrac{e^{i{\scriptstyle\theta\over\scriptstyle 2}}\left( e^{i{\scriptstyle\theta\over\scriptstyle 2}} + e^{-i{\scriptstyle\theta\over\scriptstyle 2} }\right)}{e^{i{\scriptstyle\theta\over\scriptstyle 2}}\left( e^{i{\scriptstyle\theta\over\scriptstyle 2}} - e^{-i{\scriptstyle\theta\over\scriptstyle 2} }\right)}=i\dfrac{\cos {\scriptstyle\theta\over\scriptstyle 2}}{\sin {\scriptstyle\theta\over\scriptstyle 2}}=i\mathop{\mathrm{cotan}}{\scriptstyle\theta\over\scriptstyle 2}\in i\mathbb{R}.\]

  • si \(A\) est le point du plan complexe d’affixe \(z\), \(B\) celui d’affixe \(1\) et \(C\) celui d’affixe \(-1\), \(ABC\) est un triangle inscrit dans le cercle unité et \(BC\) est un diamètre de ce cercle. Par application du théorème de la médiane, \(ABC\) est donc rectangle en \(A\) et \(\arg \left(\dfrac{z+1}{z-1}\right) \equiv {\scriptstyle\pi\over\scriptstyle 2} ~\left[\pi\right]\). On en déduit que \(\dfrac{z+1}{z-1}\) est un imaginaire pur.


Exercice 686 **

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Déterminer les points \(M\) du plan d’affixe \(z\) tels que :

  1. \(\dfrac{z+1}{z-1}\in\mathbb{R}\).

  2. \(\dfrac{z+1}{z-1}\in i\mathbb{R}\).

  3. \(\left|\dfrac{z+1}{z-1}\right|=1\).


[ID: 57] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 686
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

Soit \(z\in\mathbb{C}\setminus\left\{1\right\}\). Supposons que \(M\) est le point du plan complexe d’affixe \(z\), \(A\) est celui d’affixe \(1\) et \(B\) est celui d’affixe \(-1\). On a : \(MA=\left|z-1\right|\), \(MB=\left|z+1\right|\) et \(\left(\widehat{\overrightarrow{MB},\overrightarrow{MA}}\right) = \arg{\left({\scriptstyle z+1\over\scriptstyle z-1}\right)}\).

  1. Supposons que : \(\dfrac{z+1}{z-1}\in\mathbb{R}\). Alors soit ce quotient est nul, dans quel cas \(M=B\), soit \(\left(\widehat{\overrightarrow{MB},\overrightarrow{MA}}\right) \equiv 0 ~ \left[\pi\right]\) et donc les points \(A,B, M\) sont alignés. La réciproque est évidente. Par conséquent : \(\left\{z\in\mathbb{C}~|~ {\scriptstyle z+1\over\scriptstyle z-1}\in\mathbb{R}\right\} = \boxed{\mathbb{R}\setminus\left\{1\right\}}\).

  2. Supposons que : \({\scriptstyle z+1\over\scriptstyle z-1}\in i\mathbb{R}\). Alors : \(\left(\widehat{\overrightarrow{MB},\overrightarrow{MA}}\right) \equiv {\scriptstyle\pi\over\scriptstyle 2} ~ \left[\pi\right]\). Le triangle \(MBC\) est donc rectangle en \(A\) et d’après le théorème de la médiane, \(M\) est un point de cercle de diamètre \(\left[A,B\right]\), c’est-à-dire un point du cercle unité différent de \(A\). La réciproque est immédiate. Donc : \(\left\{z\in\mathbb{C}~|~{\scriptstyle z+1\over\scriptstyle z-1}\in i\mathbb{R} \right\}=\boxed{\mathbb U\setminus\left\{1\right\}}\).

  3. Supposons enfin que :\(\left|{\scriptstyle z+1\over\scriptstyle z-1}\right|=1\). Alors : \(\left|z-1\right|=\left|z+1\right|\) , ce qui s’écrit aussi : \(AM=BM\). Donc \(M\) est un point de la médiatrice du segment \(\left[A,B\right]\) qui est l’axe imaginaire. Par conséquent : \(z\in i\mathbb{R}\). La réciproque est triviale et \(\left\{z\in\mathbb{C}~|~\left|{\scriptstyle z+1\over\scriptstyle z-1}\right|=1\right\}=\boxed{i\mathbb{R}}\).


Une caractérisation des triangles équilatéraux **

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Soient \(A\), \(B\) et \(C\) trois points du plan complexe d’affixes respectives \(a\), \(b\) et \(c\). Montrer l’équivalence des assertions suivantes :

  1. \(ABC\) est un triangle équilatéral.

  2. \(j\) ou \(j^2\) est racine du polynôme \(P=aX^2+bX+c\).


[ID: 59] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution


Exercice 432 **

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Dans le plan muni d’un repère orthonormé direct \((O,\overrightarrow{\imath},\overrightarrow{\jmath})\), on considère un cercle de centre \(O\) sur lequel on place, dans le sens trigonométrique direct, 6 points distincts \(A,B,C,D,E\) et \(F\) de façon à ce que les triangles \(OAB\), \(OCD\) et \(OEF\) soient équilatéraux. On note \(M,N\) et \(P\) les milieux respectifs de \(\left[BC\right]\), \(\left[DE\right]\) et \(\left[FA\right]\). On veut montrer que \(MNP\) est équilatéral.

  1. Effectuer un dessin à la règle et au compas.

  2. On note \(z\), \(z'\) et \(z''\) les affixes respectives de \(A\),\(C\) et \(E\). Donner les affixes \(z_B\), \(z_D\) et \(z_F\) des points \(B\), \(D\) et \(F\) en fonction de \(z\), \(z'\) et \(z''\).

  3. Donner les affixes \(z_M\), \(z_N\) et \(z_P\) des points \(M\),\(N\) et \(P\) en fonction de \(z\), \(z'\) et \(z''\).

  4. Conclure (on pourra utiliser l’exercice ).


[ID: 61] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 432
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

  2. Le triangle \(OAB\) est équilatéral. Par conséquent, \(\boxed{z_B=e^{i{\scriptstyle\pi\over\scriptstyle 3}}z}\). De même, on montre que \(\boxed{z_D=e^{i{\scriptstyle\pi\over\scriptstyle 3}}z'}\) et \(\boxed{z_F=e^{i{\scriptstyle\pi\over\scriptstyle 3}}z''}\).

  3. Comme \(M\) est le milieu de \(\left[BC\right]\), \(z_M={\scriptstyle z_B+z_C\over\scriptstyle 2}=\boxed{{\scriptstyle e^{i{\scriptstyle\pi\over\scriptstyle 3}}z+z'\over\scriptstyle 2}}\). De même, on montre que : \(z_N=\boxed{{\scriptstyle e^{i{\scriptstyle\pi\over\scriptstyle 3}}z'+z''\over\scriptstyle 2}}\) et que \(z_P=\boxed{{\scriptstyle e^{i{\scriptstyle\pi\over\scriptstyle 3}}z''+z\over\scriptstyle 2}}\).

  4. On utilise le critère prouvé dans l’exercice . Pour montrer que \(MNP\) est équilatéral, il suffit de montrer que \(z_M+j z_N+j^2 z_P=0\). On a : \[\begin{aligned} a_M+jz_N+j^2 z_P&=&{\scriptstyle 1\over\scriptstyle 2}\left(e^{i{\scriptstyle\pi\over\scriptstyle 3}}z+z' +j\left(e^{i{\scriptstyle\pi\over\scriptstyle 3}}z'+z''\right)+j^2\left({\scriptstyle e^{i{\scriptstyle\pi\over\scriptstyle 3}}z''+z\over\scriptstyle 2}\right) \right)\\ &=&{\scriptstyle 1\over\scriptstyle 2} \left( \underbrace{\left(e^{i{\scriptstyle\pi\over\scriptstyle 3}}+j^2\right)}_{\alpha}z+\underbrace{\left(1+je^{i{\scriptstyle \pi\over\scriptstyle 3}}\right)}_{\beta}z`' +\underbrace{ \left( j+j^2e^{i{\scriptstyle\pi\over\scriptstyle 3}} \right) }_{\gamma} z''\right)\end{aligned}\] mais

    • \(j^2=-\left(1+j\right)=-e^{i{\scriptstyle\pi\over\scriptstyle 3}}\) donc \(\alpha=0\).

    • \(je^{i{\scriptstyle\pi\over\scriptstyle 3}}=j\left(1+j\right)=j+j^2=-1\) donc \(\beta=0\).

    • \(j^2 e^{i{\scriptstyle\pi\over\scriptstyle 3}}=j^2\left(1+j\right)=j^2+1=-j\) donc \(\gamma=0\).

    ce qui prouve le résultat.


Formule de Heron **

27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Les-mathematiques.net


Soit \(I\) le centre du cercle inscrit au triangle \(ABC\). Les longueurs des côtés sont \(a = y+z\), \(b = z+x\) et \(c = x+y\). On appelle \(s\) le demi-périmètre \(x+y+z\). Les angles en \(I\) vérifient \(\alpha+\beta+\gamma = \pi\).

  1. Démontrer que \(r+ix = ue^{i\alpha}\).

  2. Calculer \((r+ix)(r+iy)(r+iz)\).

  3. En prenant les parties imaginaires, démontrer que \(xyz = r^2(x+y+z)\).

  4. En déduire que \(r = \sqrt{\dfrac{(s-a)(s-b)(s-c)}{s}}\).

  5. Démontrer que l’aire du triangle \(ABC\) vaut
    \(\mathscr A = \dfrac{ra}{2} + \dfrac{rb}{2} + \dfrac{rc}{2} = \sqrt{s(s-a)(s-b)(s-c)}\) (Formule de Heron)



[ID: 63] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Formule de Heron
Par Alain Soyeur Emmanuel Vieillard-Baron le 27 novembre 2020 16:53

  1. Dans le triangle \(AIH\) rectangle en \(H\), \(r = u\cos\alpha\) et \(x= u\sin\alpha\), d’où \(r+ix = u(\cos\alpha+i\sin\alpha) = ue^{i\alpha}\).

  2. \((r+ix)(r+iy)(r+iz) = ue^{i\alpha}ve^{i\beta}we^{i\gamma} = uvwe^{i(\alpha+\beta+\gamma)} = uvwe^{i\pi} = -uvw\).

  3. En prenant les parties imaginaires, on a \(0 = r^2z + r^2y + r^2x - xyz\), d’où le résultat.

  4. On en déduit \(r^2s = xyz\). Or \(s = x + (y+z) = x+a\) d’où \(x = s-a\). Donc \(xyz = (s-a)(s-b)(s-c)\) et donc \(r^2 = \dfrac{(s-a)(s-b)(s-c)}{s}\), d’où le résultat.

  5. L’aire du triangle \(ABC\) égale l’aire de \(BIC\) + celle de \(CIA\) + celle de \(AIB\) à savoir \(\dfrac{ra}{2} + \dfrac{rb}{2} + \dfrac{rc}{2}\).

    Donc \(\mathscr A = \dfrac{ra}{2} + \dfrac{rb}{2} + \dfrac{rc}{2} = \dfrac r2 (a+b+c) = rs = s\sqrt{\dfrac{(s-a)(s-b)(s-c)}{s}} = \sqrt{s(s-a)(s-b)(s-c)}\).


Exercice 795 *

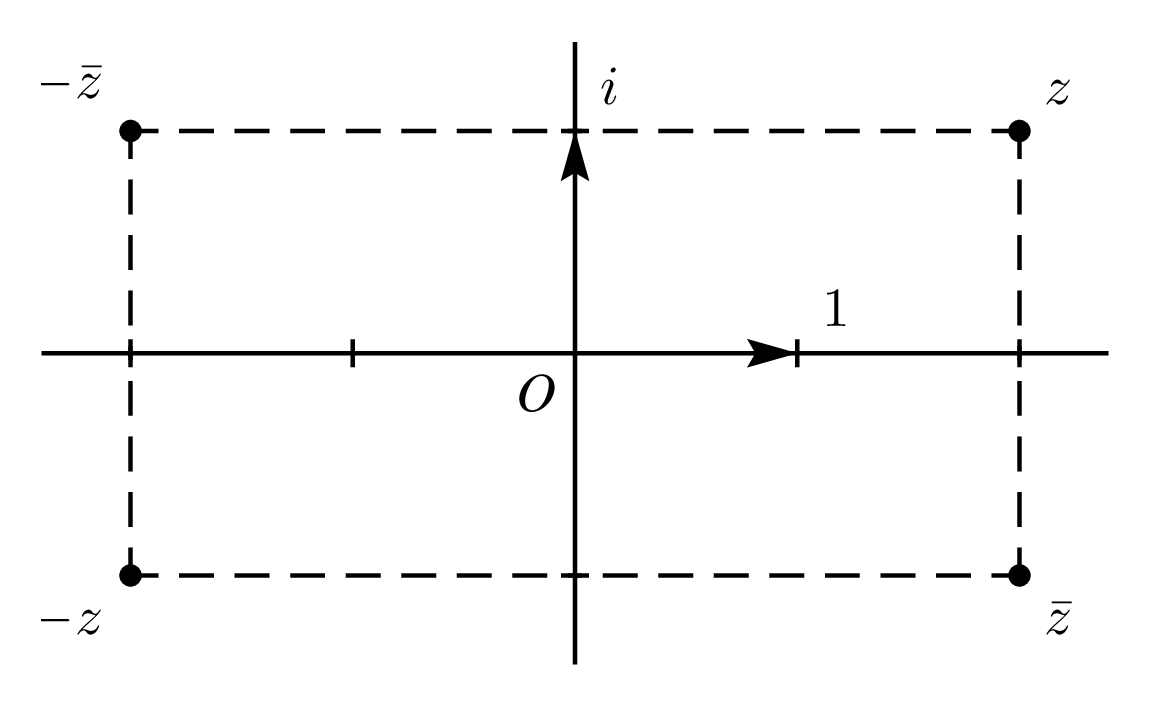
27 novembre 2020 16:53 — Par Alain Soyeur Emmanuel Vieillard-Baron

Sot \(z\) un nombre complexe non nul. Placer sur un dessin les points d’affixes respectives

  1. \(z\), \(-z\), \(\overline z\) et \(-\overline z\).

  2. \(z\), \(2z\), \(iz\), \(i\overline z\) et \(z+1+i\) et \(\sqrt{2}\left(1+i\right)z\).

  3. \(z\), \(z^{-1}\), \(\overline z\) et \(z^3\) si \(\left|z\right|=1\).


[ID: 39] [Date de publication: 27 novembre 2020 16:53] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 2 ] [Auteur(s): Alain Soyeur Emmanuel Vieillard-Baron ]
Solution

Exercice 795
Par Emmanuel Vieillard-Baron le 27 novembre 2020 17:23

Pour tout l’exercice, on appelle \(M\) le point d’affixe \(z\).

  1. On utilise que \(\bar z\) est déduit de \(z\) par la symétrie d’axe les abscisses et que \(-z\) est déduit de \(z\) par la symétrie de centre \(O\).
    image
    Les-mathematiques.net

  2. Multiplier \(z\) par un réel non nul \(k\) revient à appliquer au point \(M\) l’homothétie de centre \(O\) et de rapport \(k\). Multiplier \(z\) par \(i\) revient à appliquer à \(M\) la rotation de centre \(O\) et d’angle \(\pi/2\). Ajouter au complexe \(z\) un complexe \(z_0\) revient à appliquer à \(M\) une translation de vecteur d’affixe \(z_0\). Comme \(\sqrt{2}\left(1+i\right)=2e^{i\pi/4}\), multiplier \(z\) par \(\sqrt{2}\left(1+i\right)z\) revient à appliquer à \(z\) la similitude de centre \(O\), de rapport \(2\) et d’angle \(\pi/4\).
    image
    Les-mathematiques.net

  3. Si \(z\in\mathbb U\) alors d’après le cours, \(z^{-1}=\bar z\). Par ailleurs, \(z=e^{i\theta}\) où \(\theta\) est un argument de \(z\). Donc \(z^3=e^{3i\theta}\) et on peut alors placer le point d’affixe \(z^3\).
     
    image
    Les-mathematiques.net


Équations affines **

11 mars 2024 22:38 — Par Michel Quercia

  1. Montrer que toute droite du plan a pour équation complexe : \(az + \overline{az} = b\) avec \(a\in \mathbb{C}^*\), \(b\in \mathbb{R}\).

  2. Soient \(a,b,c\in \mathbb{C}\), \(a,b\) non tous deux nuls. Discuter la nature de \(E = \{ z \in \mathbb{C}\text{ tq }az + b\overline{z} = c \}\).


[ID: 3360] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Équations affines
Par Michel Quercia le 11 mars 2024 22:38

  1. si \(|a| \neq |b|\) : une solution unique, si \(|a| = |b|\) : une droite ou \(\emptyset\).


Transformation homographique **

11 mars 2024 22:38 — Par Michel Quercia

Soit \(f : \mathbb{C}\setminus \{ i\} \rightarrow \mathbb{C}\setminus \{ 1\} , z \mapsto \dfrac {z+i}{z-i}\)

  1. Montrer que \(f\) est bijective.

  2. Déterminer \(f(\mathbb{R})\), \(f(\mathbb U\setminus \{ i\} )\), \(f(i\mathbb{R}\setminus \{ i\} )\).


[ID: 3362] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Transformation homographique
Par Michel Quercia le 11 mars 2024 22:38

  1. \(\mathbb U\setminus \{ 1\}\), \(i\mathbb{R}\), \(\mathbb{R}\setminus \{ 1\}\).


Triangle équilatéral **

11 mars 2024 22:38 — Par Michel Quercia

Soient \(a,b,c\in \mathbb{C}\) distincts. Montrer que les propositions suivantes sont équivalentes :

  1. \(\{ a,b,c\}\) est un triangle équilatéral.

  2. \(j\) ou \(j^2\) est racine de \(az^2 + bz + c = 0\).

  3. \(a^2 + b^2 + c^2 = ab + ac + bc\).

  4. \(\dfrac 1{a-b} + \dfrac 1{b-c} + \dfrac 1{c-a} = 0\).


[ID: 3364] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Sommets d’un carré **

11 mars 2024 22:38 — Par Michel Quercia

Soient \(a,b,c,d \in \mathbb{C}\) tels que \(a+ib=c+id\) et \(a+c= b+d\).

Que pouvez-vous dire des points d’affixes \(a,b,c,d\) ?

En déduire qu’il existe \(z \in \mathbb{C}\) tel que \((z-a)^4 = (z-b)^4 = (z-c)^4 = (z-d)^4\).


[ID: 3365] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Sommets d’un carré
Par Michel Quercia le 11 mars 2024 22:38

Les diagonales se coupent en leurs milieux, ont même longueur, et sont perpendiculaires ; c’est un carré.


Configuration de points **

11 mars 2024 22:38 — Par Michel Quercia

Déterminer les nombres \(z\in \mathbb{C}\) tels que

  1. \(z,z^2 ,z^4\) sont alignés.

  2. \(1,z,z^2\) forment un triangle rectangle.

  3. \(z,\dfrac 1z,-i\) sont alignés.


[ID: 3367] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Configuration de points
Par Michel Quercia le 11 mars 2024 22:38

  1. \(z\in \mathbb{R}\) ou \(\mathop{\mathrm{Re}}z=-{1/2}\).

  2. \(z \in -1 + i\mathbb{R}\) ou \(z \in i\mathbb{R}\) ou \(|z+{1/2}| = {1/2}\).

  3. \(z\in i\mathbb{R}\) ou \(|z-i| = \sqrt 2\).


\(a+b+c=1\) **

11 mars 2024 22:38 — Par Michel Quercia

Trouver \(a,b,c\in \mathbb U\) tels que \(a+b+c = 1\) et \(abc = 1\).


[ID: 3369] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

\(a+b+c=1\)
Par Michel Quercia le 11 mars 2024 22:38

\((0,a,a+b,a+b+c = 1)\) forme un losange donc l’un des nombres vaut \(1\) et les deux autres sont opposés : \(\{ a,b,c\} = \{ 1,i,-i\}\).


\(u+v+w = 0\) **

11 mars 2024 22:38 — Par Michel Quercia

Soient \(u,v,w\) trois complexes unitaires tels que \(u+v+w = 0\). Montrer que \(u=jv=j^2 w\) ou \(u=jw=j^2 v\).


[ID: 3371] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

\(z+1/z = 2\) **

11 mars 2024 22:38 — Par Michel Quercia

Trouver les complexes \(z \in \mathbb{C}^*\) tels que \(\left|z + \dfrac 1z\right| = 2\).


[ID: 3372] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

\(z+1/z = 2\)
Par Michel Quercia le 11 mars 2024 22:38

Poser \(z=x+iy\). On trouve les cercles de centre \(\pm i\) et de rayon \(\sqrt 2\) (laborieux).


Symétrique par rapport à une droite **

11 mars 2024 22:38 — Par Michel Quercia

Les points \(A,B,M\) ayant pour affixes \(a,b,z\), calculer l’affixe du symétrique de \(M\) par rapport à la droite \((AB)\).


[ID: 3374] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Symétrique par rapport à une droite
Par Michel Quercia le 11 mars 2024 22:38

\(z' = \dfrac {(b-a)\overline z + a\overline b - \overline ab} {\overline b - \overline a}\).


Orthocentre **

11 mars 2024 22:38 — Par Michel Quercia

Soient \(a,b,c,d\in \mathbb{C}\) deux à deux distincts. Montrer que si deux des rapports \(\dfrac {d-a}{b-c}, \dfrac {d-b}{c-a}, \dfrac {d-c}{a-b}\) sont imaginaires purs, alors le troisième l’est aussi.


[ID: 3376] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Orthocentre
Par Michel Quercia le 11 mars 2024 22:38

\(d =\) orthocentre de \(abc\).


Similitudes dans un triangle **

11 mars 2024 22:38 — Par Michel Quercia

On donne un triangle \(ABC\), un réel positif \(k\) et un angle \(\theta\). On note \(S_M\) la similitude directe de centre \(M\), de rapport \(k\) et d’angle \(\theta\). Soit \(C_{1}\) déduit de \(C\) par \(S_A\), \(B_{1}\) déduit de \(B\) par \(S_C\), \(A_{1}\) déduit de \(A\) par \(S_B\). Montrer que les deux triangles \(ABC\) et \(A_{1}B_{1}C_{1}\) ont même centre de gravité.


[ID: 3378] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Centre du cercle circonscrit **

11 mars 2024 22:38 — Par Michel Quercia

Soient \(a,b,c\in \mathbb{C}\), affixes de points \(A,B,C\) non alignés. Calculer l’affixe du centre du cercle circonscrit à \(ABC\) en fonction de \(a,b,c\).


[ID: 3379] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Centre du cercle circonscrit
Par Michel Quercia le 11 mars 2024 22:38

\(\omega = \dfrac {a(c\overline c-b\overline b) + b(a\overline a-c\overline c) + c(b\overline b-a\overline a)} {a(\overline c-\overline b) + b(\overline a-\overline c) + c(\overline b-\overline a)}\).


Sphère de \(\mathbb{R}^3\) **

11 mars 2024 22:38 — Par Michel Quercia

Soient \(u,v \in \mathbb{C}\) tels que \(u+v\neq 0\). On pose \(x = \dfrac {1+uv}{u+v}\), \(y = i\dfrac {1-uv}{u+v}\), \(z = \dfrac {u-v}{u+v}\).

  1. CNS sur \(u\) et \(v\) pour que \(x,y,z\) soient réels ?

  2. On suppose cette condition réalisée. Montrer que le point \(M(x,y,z)\) dans l’espace appartient à la sphère de centre \(O\) et de rayon 1.

  3. A-t-on ainsi tous les points de cette sphère ?


[ID: 3381] [Date de publication: 11 mars 2024 22:38] [Catégorie(s): Application des nombres complexes à la géométrie ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Sphère de \(\mathbb{R}^3\)
Par Michel Quercia le 11 mars 2024 22:38

  1. \(z\in \mathbb{R}\Leftrightarrow \exists \alpha \in \mathbb{R}\) tq \(u=\alpha v\).

    \(x,y\in \mathbb{R}\Leftrightarrow \alpha =1/|v|^2 \Leftrightarrow u=1/{\overline v}\).

  2. il manque seulement les deux pôles.


Les-Mathematiques.net Mathématiques vivantes

Thématiques

;
Success message!