Fonctions exponentielles, logarithmes et puissances

  1. Les exercices
  2. Vue compacte

Exercices du dossier Fonctions exponentielles, logarithmes et puissances

Inégalité de convexité **

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

  1. Montrer que : \[\forall x>-1,\quad \ln\left(1+x\right)\leqslant x\]

  2. En déduire que : \[\forall n> 1,\quad \left(1+{\scriptstyle 1\over\scriptstyle n}\right)^n \leqslant e \leqslant\left(1-{\scriptstyle 1\over\scriptstyle n}\right)^{-n}\]


[ID: 298] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Inégalité de convexité
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

  1. Il suffit, pour montrer cette inégalité, d’étudier les variations de \(\theta: \left\{ \begin{array}{ccl} \left]-1,+\infty\right] & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \ln\left(1+x\right) - x \end{array} \right.\).

  2. Soit \(n >1\). Appliquant l’inégalité précédente avec \(x={\scriptstyle 1\over\scriptstyle n}\), on a : \(\ln\left(1+{\scriptstyle 1\over\scriptstyle n}\right)\leqslant{\scriptstyle 1\over\scriptstyle n}\) ce qui amène :
    \(n\ln\left(1+{\scriptstyle 1\over\scriptstyle n}\right)\leqslant 1\) et, la fonction exponentielle étant strictement croissante : \(e^{n\ln\left(1+{\scriptstyle 1\over\scriptstyle n}\right)}\leqslant e\). Par conséquent : \(\left(1+{\scriptstyle 1\over\scriptstyle n}\right)^n \leqslant e\). De même, comme \(n>1\), \(-{\scriptstyle 1\over\scriptstyle n} > -1\) et on peut appliquer la première question avec \(x=-{\scriptstyle 1\over\scriptstyle n}\), on obtient : \(\ln\left(1-{\scriptstyle 1\over\scriptstyle n}\right) \leqslant-{\scriptstyle 1\over\scriptstyle n}\). Multipliant les deux membres de cette inégalité par \(-n\), on a : \(-n \ln\left(1-{\scriptstyle 1\over\scriptstyle n}\right) \geqslant 1\) et donc, passant comme précédemment à l’exponentielle : \(e \leqslant\left(1-{\scriptstyle 1\over\scriptstyle n}\right)^{-n}\).


Exercice 190 *

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

Posons, pour \(x\in\mathbb{R}_+^*\)  : \[a=\exp \left(x^2\right) \quad \textrm{ et} \quad b=\dfrac{1}{x}\ln\left(x^{{\scriptstyle 1\over\scriptstyle x}}\right)\] Simplifier \(a^b\).


[ID: 300] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Exercice 190
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

Soit \(x\in\mathbb{R}_+^*\). Remarquons que \(b=\dfrac{1}{x^2}\ln\left(x\right)\) donc \[\begin{aligned} a^b &=& \left(e^{x^2}\right)^{{\scriptstyle 1\over\scriptstyle x^2}\ln\left(x\right)}\\ &=& e^{{\scriptstyle x^2\over\scriptstyle x^2}\ln\left(x\right)}\\ &=& \exp\left(\ln x\right)\\ &=& x\end{aligned}\]


Des équations **

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

Résoudre les équations suivantes après avoir déterminé leur domaine de validité :

  1. \(\ln\left(x-1\right)=\ln\left(3x-5\right)\)

  2. \(\ln\left(\sqrt{2x-3}\right)=\ln\left(6-x\right)-{\scriptstyle 1\over\scriptstyle 2}\ln x\)

  3. \(2\ln x=\ln\left(x+4\right)+\ln \left(2x\right)\)

  4. \(e^{4x}-3e^{2x}-4=0\).

  5. \(8^{6x}-3.8^{3x}-4=0\).

  6. \(x^{\sqrt x}=(\sqrt x)^x\)

  7. \(2^{x^3}=3^{x^2}\)

  8. \(\log_a x = \log_x a\) où \(a\in\mathbb{R}_+^*\setminus\left\{1\right\}\)

  9. \(\log_3 x - \log_2 x = 1\).

  10. \(2^x+2^{x+1}+...+2^{x+n}=3^x+3^{x+1}+...+3^{x+n}\) où \(n\in \mathbb{N}\)


[ID: 302] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Des équations
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

  1. domaine de validité :\(\left] {\scriptstyle 5\over\scriptstyle 3},+\infty\right[\). \[\begin{aligned} & &\ln\left(x-1\right)=\ln\left(3x-5\right)\\ &\Rightarrow & x-1 = 3x-5\\ &\Rightarrow &x=2\end{aligned}\] Réciproquement est solution de cette équation.

  2. domaine de validité :\(\left] {\scriptstyle 3\over\scriptstyle 2},6\right[\). \[\begin{aligned} & &\ln\left(\sqrt{2x-3}\right)=\ln\left(6-x\right)-{\scriptstyle 1\over\scriptstyle 2}\ln x\\ &\Rightarrow &\ln\left(\sqrt{2x-3}\right)=\ln\left( \dfrac{6-x}{\sqrt{x} }\right)\\ &\Rightarrow & \sqrt{2x-3} = \dfrac{6-x}{\sqrt{x} }\end{aligned}\] Mais : \[\begin{aligned} &&\sqrt{2x-3} = \dfrac{6-x}{\sqrt{x} }\\ &\Rightarrow & x\left(2x-3\right) = \left(6-x\right)^2 \\ &\Rightarrow & x(x+8)=0\\ &\Rightarrow & x=0 \quad \textrm{ ou} \quad x=-8\end{aligned}\] Aucun de ces nombres n’est admissible, il n’y a pas de solution.

  3. \[\begin{aligned} & &2\ln x=\ln\left(x+4\right)+\ln \left(2x\right)\\ &\Rightarrow & \ln\left( \dfrac{2x\left(x+4\right)}{x^2} \right) =0\\ &\Rightarrow & \dfrac{2x\left(x+4\right)}{x^2} = 1\\ &\Rightarrow & x^2+9x-36=0\\ &\Rightarrow & x=3 \quad \textrm{ ou} \quad x=-12\end{aligned}\] Mais \(-12\) ne vérifie pas l’équation. On vérifie par contre que \(3\) la vérifie. et l’unique solution de l’équation est .

  4. On a  : \[\begin{aligned} & &e^{4x}-3e^{2x}-4=0\\ &\Rightarrow &\begin{cases} X = e^{2x} \\ X^2-3X-4=0 \end{cases}\\ &\Rightarrow & \begin{cases} X = e^{2x} \\ X=4 \quad \textrm{ ou} \quad X=-1 \end{cases}\\ &\Rightarrow & e^{2x} = 4 \quad \textrm{ (On ne peut avoir $e^{2x}=-1$ !) }\\ &\Rightarrow & x=\ln 2\end{aligned}\] Réciproquement, on montre que est bien solution de l’équation.

  5. Cette équation est valide sur \(\mathbb{R}\). On a la série d’implications : \[\begin{aligned} & &8^{6x}-3.8^{3x}-4=0 \\ &\Rightarrow &\begin{cases} X^2-3X-4=0 \\ X=8^{3x} \end{cases}\\ &\Rightarrow &\begin{cases}X=-1 \quad \textrm{ ou} \quad X=4 \\ X=8^{3x}\end{cases}\\ &\Rightarrow & 8^{3x} = -1 (\textrm{ impossible} ) \quad \textrm{ ou} \quad 8^{3x} = 4\\ &\Rightarrow & x= {\scriptstyle 2\over\scriptstyle 9}\end{aligned}\] Réciproquement, on vérifie que \(\fbox{$ {\scriptstyle 2\over\scriptstyle 9}$}\) est bien solution de l’équation.

  6. \[\begin{aligned} & &x^{\sqrt x}=(\sqrt x)^x\\ &\Rightarrow &\sqrt{x}\ln x = x\ln \sqrt{x}\\ &\Rightarrow &\sqrt{x}\ln x - {\scriptstyle x\over\scriptstyle 2}\ln x = 0\\ &\Rightarrow & \sqrt{x}\left(1 - {\scriptstyle\sqrt{x}\over\scriptstyle 2} \right)\ln x = 0\\ &\Rightarrow & \sqrt{x} = 0 \quad \textrm{ ou} \quad 1 - {\scriptstyle\sqrt{x}\over\scriptstyle 2} = 0 \quad \textrm{ ou} \quad\ln x = 0\\ &\Rightarrow & x=0 \quad \textrm{ ou} \quad x = 4 \quad \textrm{ ou} \quad x=1\end{aligned}\] Réciproquement, seuls sont solutions de l’équation.

  7. \[\begin{aligned} & & 2^{x^3}=3^{x^2}\\ &\Rightarrow &x^3 \ln 2 = x^2 \ln 3\\ &\Rightarrow & x^2\left( x\ln 2 - \ln 3\right) = 0\\ &\Rightarrow & x=0 \quad \textrm{ ou} \quad x= \dfrac{\ln 3}{\ln 2}\end{aligned}\] Réciproquement, ces deux nombres sont solutions donc les solutions de l’équation sont : .

  8. \[\begin{aligned} & &\log_a x = \log_x a\\ &\Rightarrow & \dfrac{\ln x}{\ln a} = \dfrac{\ln a}{\ln x} \\ &\Rightarrow & \ln^2 x - \ln ^2 a = 0\\ &\Rightarrow & \left(\ln x - \ln a\right) \left(\ln x + \ln a\right) =0\\ &\Rightarrow & x=a \quad \textrm{ ou} \quad x= {\scriptstyle 1\over\scriptstyle a} \end{aligned}\] Réciproquement, les nombres sont bien solutions de l’équation.

  9. \[\begin{aligned} & &\log_3 x - \log_2 x = 1\\ &\Rightarrow & \dfrac{\ln x}{\ln 3} - \dfrac{\ln x}{\ln 2} = 1\\ &\Rightarrow & \dfrac{\ln 2 - \ln 3}{\ln 3 \ln 2} \ln x = 1\\ &\Rightarrow & x=\exp\left( \dfrac{\ln 3 \ln 2}{ \ln {\scriptstyle 2\over\scriptstyle 3}} \right)\end{aligned}\] Réciproquement est solution de l’équation.

  10. On reconnaît des sommes géométriques : \[\begin{aligned} & &2^x+2^{x+1}+...+2^{x+n}=3^x+3^{x+1}+...+3^{x+n} \\ &\Rightarrow &2^x\left(1 + 2 + \dots+ 2^n\right) = 3^x\left(1+3+\dots+3^n\right)\\ &\Rightarrow & \left({\scriptstyle 2\over\scriptstyle 3}\right)^x = \dfrac{\dfrac{1-3^{n+1}}{1-3} }{\dfrac{1-2^{n+1}}{1-2}}\\ &\Rightarrow & \left({\scriptstyle 2\over\scriptstyle 3}\right)^x = \dfrac{1}{2}\dfrac{3^{n+1} - 1}{2^{n+1} - 1}\\ &\Rightarrow & x= \dfrac{\ln\left( \dfrac{1}{2}\dfrac{3^{n+1} - 1}{2^{n+1} - 1}\right)}{\ln {\scriptstyle 2\over\scriptstyle 3}}\end{aligned}\] Réciproquement, on vérifie que  : est bien solution de l’équation.


Des inéquations **

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

Résoudre les inéquations suivantes après avoir donné leur domaine de validité :

  1. \(\ln\left(x^2-2x\right)>\ln\left(4x-5\right)\)

  2. \(e^{x^2}>\left(e^x\right)^4\times e\).

  3. \(a^{x^2} < (\sqrt{a})^{7x-3}\) où \(a\in\mathbb{R}_+^*\setminus \{1\}\).


[ID: 304] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Des inéquations
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

  1. On vérifie que l’inéquation n’est valide que si \(x>2\). \[\begin{aligned} & &\ln\left(x^2-2x\right)>\ln\left(4x-5\right)\\ &\Rightarrow & x^2-2x >4x-5 \quad \textrm{ car $\ln$ est croissante }\\ &\Rightarrow & x^2 - 6x+5>0\\ &\Rightarrow & x\in \left]-\infty,1\right[\cup \left]5,+\infty\right[\end{aligned}\] Compte tenu du domaine de validité de l’inéquation, \(\ln\left(x^2-2x\right)>\ln\left(4x-5\right)\) seulement si \(x>5\). Réciproquement, on montre que si alors l’inéquation est vérifiée.

  2. L’inéquation est valide sur \(\mathbb{R}\). \[\begin{aligned} & &e^{x^2}>\left(e^x\right)^4\times e\\ &\Longleftrightarrow&e^{x^2 - 1 } > e^{4x} \\ &\Longleftrightarrow& x^2 - 1 >4x \quad \textrm{ car $\exp$ est croissante}\\ &\Longleftrightarrow& x^2-4x-1>0 \\ &\Longleftrightarrow& x\in\left]-\infty,2-\sqrt{5}\right[ \cup \left]2+\sqrt{5},+\infty\right[\end{aligned}\] L’ensemble solution de l’inéquation est donc :

  3. L’inéquation est valide sur \(\mathbb{R}\). \[\begin{aligned} & &a^{x^2} < (\sqrt{a})^{7x-3}\\ &\Longleftrightarrow&x^2 \ln a < \dfrac{7x-3}{2} \ln a \quad \textrm{ car $\ln$ est croissante }\\ \end{aligned}\] Lorsque \(\ln a>0\) c’est-à-dire lorsque \(a>1\), \[\begin{aligned} & &a^{x^2} < (\sqrt{a})^{7x-3}\\ &\Longleftrightarrow& x^2 < \dfrac{7x-3}{2} \quad \textrm{ car $a\neq 1$ donc $\ln a\neq 0$}\\ &\Longleftrightarrow& 2x^2 -7x+3 <0\\ &\Longleftrightarrow& x\in\left]{\scriptstyle 1\over\scriptstyle 2},3\right[\end{aligned}\] L’inégalité est vraie si et seulement si .

    Lorsque \(\ln a<0\) c’est-à-dire lorsque \(0<a<1\), \[\begin{aligned} & &a^{x^2} > (\sqrt{a})^{7x-3}\\ &\Longleftrightarrow& x^2 > \dfrac{7x-3}{2} \\ &\Longleftrightarrow& 2x^2 -7x+3 >0\\ &\Longleftrightarrow& x\in\left]-\infty,{\scriptstyle 1\over\scriptstyle 2}\right[ \cup \left]3,+\infty\right[\end{aligned}\] L’inégalité est vraie si et seulement si .


Des limites **

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

Déterminer les limites suivantes:

  1. \(\displaystyle{\lim_{x\longrightarrow +\infty} x^{ {\scriptstyle 1\over\scriptstyle x}}}\)

  2. \(\displaystyle{\lim_{x\longrightarrow 0^+} x^{ \sqrt{x}}}\)

  3. \(\displaystyle{\lim_{x\longrightarrow 0^+} x^{ {\scriptstyle 1\over\scriptstyle x}}}\)

  4. \(\displaystyle{\lim_{x \rightarrow +\infty}{\scriptstyle e^x +2\over\scriptstyle e^x+1}}\)

  5. \(\displaystyle{\lim_{x \rightarrow +\infty}{\scriptstyle xe^x\over\scriptstyle 3^x}}\)

  6. \(\displaystyle{\lim_{x \rightarrow -\infty}{\scriptstyle xe^x\over\scriptstyle 3^x}}\)

  7. \(\displaystyle{\lim_{x \rightarrow -\infty}x^2e^{-x}-x}\)

  8. \(\displaystyle{\lim_{x \rightarrow 0^+}x^x}\)

  9. \(\displaystyle{\lim_{x \rightarrow +\infty}{\scriptstyle\left(x^x\right)^x\over\scriptstyle x^{x^x}}}\)

  10. \(\displaystyle{\lim_{x \rightarrow +\infty}{\scriptstyle a^{\left(b^x\right)}\over\scriptstyle b^{\left(a^x\right)}}}\) où \(1<a<b\).

  11. \(\displaystyle{\lim_{x \rightarrow 0}\sqrt{x}\ln\left({\scriptstyle x^2\over\scriptstyle 1+x}\right)}\)

  12. \(\displaystyle{\lim_{x \rightarrow +\infty}\left({\scriptstyle\ln x\over\scriptstyle x}\right)^{\scriptstyle 1\over\scriptstyle x}}\)

  13. \(\displaystyle{\lim_{x \rightarrow +\infty}\left(1+{\scriptstyle 1\over\scriptstyle x}\right)^x}\)


[ID: 306] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Des limites
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

  1. \(x^{ {\scriptstyle 1\over\scriptstyle x}} = e^{\dfrac{\ln x}{x}}\) mais \(\dfrac{\ln x}{x} \xrightarrow[x\rightarrow +\infty]{} 0\) donc \(x^{ {\scriptstyle 1\over\scriptstyle x}} \xrightarrow[x\rightarrow +\infty]{} e^0 = \boxed{1}\).

  2. \(x^{\sqrt{x}} = e^{\sqrt{x}\ln x}\) mais \(\sqrt{x}\ln x =x^{{\scriptstyle 1\over\scriptstyle 2}}\ln x \xrightarrow[x\rightarrow 0^+]{} 0\) donc \(x^{\sqrt{x}} \xrightarrow[x\rightarrow 0^+]{} e^0 = \boxed{1}\).

  3. \(x^{ {\scriptstyle 1\over\scriptstyle x}} = e^{\dfrac{\ln x}{x}}\) mais \(\dfrac{\ln x}{x} \xrightarrow[x\rightarrow 0^+]{} -\infty\) donc \(x^{ {\scriptstyle 1\over\scriptstyle x}} \xrightarrow[x\rightarrow 0^+]{} \boxed{0}\).

  4. \({\scriptstyle e^x +2\over\scriptstyle e^x+1} = {\scriptstyle 1+2e^{-x}\over\scriptstyle 1+e^{-x}} \xrightarrow[x\rightarrow +\infty]{} \boxed{1}\).

  5. \({\scriptstyle xe^x\over\scriptstyle 3^x} =x\left({\scriptstyle e\over\scriptstyle 3}\right)^x = xe^{x\ln{\scriptstyle e\over\scriptstyle 3}}\) donc \({\scriptstyle xe^x\over\scriptstyle 3^x} \xlongequal{X=x\ln{\scriptstyle e\over\scriptstyle 3}} \dfrac{X}{\ln{\scriptstyle e\over\scriptstyle 3}}{e^X } \xrightarrow[X\rightarrow -\infty]{} \boxed{0}\)

  6. De la même façon, toujours parce que \(e<3\) : \(\displaystyle{\lim_{x \rightarrow -\infty}{\scriptstyle xe^x\over\scriptstyle 3^x}} = \boxed{-\infty}\).

  7. \(x^2e^{-x}-x = x^2 e^{-x} \left(1 - \dfrac{e^{x}}{x}\right)\xrightarrow[x\rightarrow -\infty]{}\boxed{+\infty}\)

  8. \(x^x = e^{x\ln x}\) mais \(x\ln x \xrightarrow[x\rightarrow 0^+]{}\) donc \(x^x \xrightarrow[x\rightarrow 0^+]{} e^0 = \boxed{1}\).t

  9. \({\scriptstyle\left(x^x\right)^x\over\scriptstyle x^{x^x}} = \dfrac{e^{x\ln\left(x^x\right)}}{e^{x^x \ln x}} = e^{\left(x^2-x^x\right)\ln x } = e^{\left(x^{2-x} -1\right)x^x \ln x}\) mais \(x^{2-x}\xrightarrow[x\rightarrow +\infty]{} 0\) donc : \(x^{2-x} -1\xrightarrow[x\rightarrow +\infty]{} -1\). Comme \(x^x \ln x \xrightarrow[x\rightarrow +\infty]{} +\infty\), par opérations sur les limites, \(\left(x^{2-x} -1\right)x^x \ln x \xrightarrow[x\rightarrow +\infty]{} -\infty\) et donc : \({\scriptstyle\left(x^x\right)^x\over\scriptstyle x^{x^x}} \xrightarrow[x\rightarrow +\infty]{} \boxed{0}\).

  10. \({\scriptstyle a^{\left(b^x\right)}\over\scriptstyle b^{\left(a^x\right)}} = \dfrac{ e^{b^x \ln a }}{e^{a^x \ln b}}=e^{a^x \ln b - b^x \ln a} = e^{b^x\ln b \left( \left({\scriptstyle a\over\scriptstyle b}\right)^x - \dfrac{\ln a}{\ln b} \right)}\) mais \(b^x\ln b \xrightarrow[x\rightarrow +\infty]{} \infty\) , \(\left({\scriptstyle a\over\scriptstyle b}\right)^x \xrightarrow[x\rightarrow +\infty]{} 0\) et \(\dfrac{\ln a}{\ln b}>0\) donc \({\scriptstyle a^{\left(b^x\right)}\over\scriptstyle b^{\left(a^x\right)}}\xrightarrow[x\rightarrow +\infty]{}\boxed{+\infty}\).

  11. \(\sqrt{x}\ln\left({\scriptstyle x^2\over\scriptstyle 1+x}\right) = 2x^{{\scriptstyle 1\over\scriptstyle 2}}\ln x - x^{{\scriptstyle 1\over\scriptstyle 2}} \ln \left({1+x}\right) \xrightarrow[x\rightarrow 0]{} \boxed{0}\)

  12. \(\left({\scriptstyle\ln x\over\scriptstyle x}\right)^{\scriptstyle 1\over\scriptstyle x} = e^{\dfrac{\ln\left({\scriptstyle\ln x\over\scriptstyle x} \right)}{x}}=e^{{\scriptstyle 1\over\scriptstyle x} \left(\ln\ln x - \ln x\right)}\) mais \(\dfrac{\ln x}{x} \xrightarrow[x\rightarrow +\infty]{} 0\) et \(\dfrac{\ln\left(\ln x\right)}{x} \xrightarrow[x\rightarrow +\infty]{} 0\) donc \(\left({\scriptstyle\ln x\over\scriptstyle x}\right)^{\scriptstyle 1\over\scriptstyle x} \xrightarrow[x\rightarrow +\infty]{} e^0 =\boxed{1}\).

  13. \(\left(1+{\scriptstyle 1\over\scriptstyle x}\right)^x = e^{x\ln\left(1+{\scriptstyle 1\over\scriptstyle x}\right)} = e^{\dfrac{\ln\left(1+{\scriptstyle 1\over\scriptstyle x}\right)}{{\scriptstyle 1\over\scriptstyle x}}}\) mais \({e^{\dfrac{\ln\left(1+{\scriptstyle 1\over\scriptstyle x}\right)}{{\scriptstyle 1\over\scriptstyle x}}}} \xlongequal{X={\scriptstyle 1\over\scriptstyle x}} {e^{\dfrac{\ln\left(1+X\right)}{X}}} \xrightarrow[X\rightarrow 0]{} e^1=\boxed{e}\).


Exercice 391 **

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

Soit un entier \(n > 1\). On considère l’équation \[x^{x^n} = n\]

  1. Montrer qu’il existe une unique solution à cette équation.

  2. Déterminer cette unique solution.


[ID: 308] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Exercice 391
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

  1. Étudions à \(n\) fixé la fonction définie par \[f(x) = x^{x^n} - n = e^{x^n \ln x}\] Elle est définie sur \(]0, +\infty[\), dérivable sur cet intervalle et \(\forall x\in I\), \[f'(x) = x^{n-1}e^{x^n\ln x}\left[ n \ln x + 1\right]\] La dérivée s’annule en un seul point \(x_0 = e^{-1/n} < 1\). On en déduit en écrivant le tableau de variations de \(f\) que \(f\) présente un minimum en \(x_0\) avec \(f(x_0) = e^{-1/(en)} - n\). Par conséquent, puisque \(f(x) \xrightarrow[x\rightarrow 0^+ \rightarrow 1]{} - n < n\), et que \(f(x) \xrightarrow[x\rightarrow +\infty \rightarrow +]{}\infty\), la fonction ne s’annule qu’une fois en un point \(x_1 > x_0\).

  2. Puisque \(f(n^{1/n}) = 0\), en en déduit que la seule solution de l’équation vaut \(n^{1/n}\).


Exercice 127 **

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

Soit \(n\in \mathbb{N}^*\). Montrer que le nombre de chiffres nécessaires pour écrire \(n\) en base \(10\) est égale à la partie entière de \(1+\log n\).


[ID: 310] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Exercice 127
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

Supposons que l’écriture de \(n\) en base 10 compte \(m+1\) chiffres \(a_m,\dots,a_0\in\llbracket 0,9\rrbracket\) avec \(a_m\neq 0\) et \(m\in\mathbb{N}\). On a alors : \(n=\sum_{k=0}^m a_k 10^k\) et \[\begin{aligned} \log n& =& \log\left(\sum_{k=0}^m a_k 10^k\right) \\ &=& \dfrac{\ln{10^m \left(a_m + a_{m-1}10^{-1}+ \dots+ a_0 10^{-m}\right)}}{\ln 10}\\ &=& m+\dfrac{\ln \left(a_m + a_{m-1}10^{-1}+ \dots+ a_0 10^{-m}\right) }{\ln 10}\end{aligned}\]

Mais \(1\leqslant a_m + a_{m-1}10^{-1}+ \dots+ a_0 10^{-m} \leqslant 10\) et \[0\leqslant\dfrac{\ln \left(a_m + a_{m-1}10^{-1}+ \dots+ a_0 10^{-m}\right) }{\ln 10}<1.\] Donc \(\boxed{E\left(1+\log n\right)=m+1}\) et le résultat est prouvé.


Exercice 460 **

11 janvier 2021 15:25 — Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur

Étudier la fonction définie par \(f(x) = x\sqrt{\dfrac{x-1}{x+1}}\).


[ID: 312] [Date de publication: 11 janvier 2021 15:25] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur ]
Solution

Exercice 460
Par Emmanuel Vieillard-Baron Bernhard Keller Alain Soyeur le 11 janvier 2021 15:25

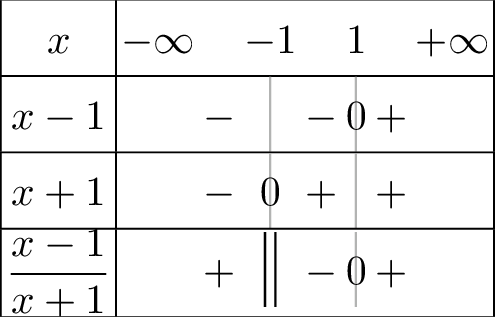
  1. Nous déduisons du tableau de signe

    Les-mathematiques.net

    que \(f\) est définie sur \(I=\left]-\infty,-1\right[\cup \left[1,+\infty\right[\).

  2. \(f\) est dérivable sur \(\left]-\infty,-1\right[\cup \left]1,+\infty\right[\) car la fonction racine carrée est dérivable sur \(\mathbb{R}_+^*\). Soit \(x\) un élément de cet ensemble. On trouve : \[f'\left(x\right)=\dfrac{x^2+x-1}{\sqrt{\dfrac{x-1}{x+1}}\left(x+1\right)^2}.\] \(f'\) est donc du signe de \(x^2+x-1\). Les racines de ce trinômes sont \(\alpha=\left(-1+\sqrt 5\right)/2\) et \(\beta=\left(-1-\sqrt 5\right)/2\). Seul \(\alpha\) est dans le domaine de définition de \(f\). Pour les limites, on remarque que : \[f\left(x\right)=x\sqrt{\dfrac{1-{\scriptstyle 1\over\scriptstyle x}}{1+{\scriptstyle 1\over\scriptstyle x}}}\] et donc \(\displaystyle{\lim_{x \rightarrow -\infty}f\left(x\right)}=-\infty\), \(\displaystyle{\lim_{x \rightarrow +\infty}f\left(x\right)}=+\infty\). Par limites usuelles, il est clair que \(\displaystyle{\lim_{x \rightarrow -1^-}f\left(x\right)}=-\infty\). On en déduit de la tableau de variation suivant :

    Les-mathematiques.net

  3. Le graphe de \(f\) admet une branche infinie quand \(x\rightarrow \pm\infty\) et quand \(x\rightarrow -1^-\).

    • \[\dfrac{f\left(x\right)}{x}=\sqrt{\dfrac{x-1}{x+1}}=\sqrt{\dfrac{1-{\scriptstyle 1\over\scriptstyle x}}{1+{\scriptstyle 1 \over\scriptstyle x}}} \xrightarrow[x\rightarrow \pm \infty]{} 1\] et par multiplication par les quantités conjuguées, \[f\left(x\right)-x = x\left(\sqrt{\dfrac{x-1}{x+1}} -1\right) =x\dfrac{\dfrac{x-1}{x+1}-1 }{ \sqrt{\dfrac{x-1}{x+1}} +1 }=\dfrac{\dfrac{-2x}{x+1} }{ \sqrt{\dfrac{x-1}{x+1}} +1 }=\dfrac{\dfrac{-2}{1+{\scriptstyle 1\over\scriptstyle x}} }{ \sqrt{\dfrac{1-{\scriptstyle 1\over\scriptstyle x}}{1+{\scriptstyle 1\over\scriptstyle x}}} +1 }\xrightarrow[x\rightarrow \pm \infty]{} -1\]

      La droite d’équation \(\boxed{y=x-1}\) est donc asymptote à la courbe au voisinage de \(+\infty\) et \(-\infty\).

    • On a une asymptote verticale au voisinage de \(-1\) d’équation \(x=-1\).

  4. On en déduit le graphe de \(f\) :

    Les-mathematiques.net


Calcul de limite **

12 mars 2024 09:54 — Par Michel Quercia

Montrer que : \(\forall x > 0\), \(x - {1/2}x^2 < \ln(1+x) < x\). En déduire \(\lim_{n\to \infty } \left(1+\dfrac 1{n^2 }\right)\left(1+\dfrac 2{n^2 }\right) \dots\left(1+\dfrac n{n^2 }\right)\).


[ID: 3459] [Date de publication: 12 mars 2024 09:54] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Dérivées de \(\exp(-1/x)\) **

12 mars 2024 09:54 — Par Michel Quercia

On pose \(f(x) = \exp(-1/x)\) si \(x > 0\) et \(f(0)=0\).

  1. Montrer que \(f\) est de classe \(\mathcal C ^\infty\) sur \(\mathbb{R}^{+*}\), et que \(f^{(n)}(x)\) est de la forme \(P_n(x)x^{-2n}\exp(-1/x)\) où \(P_n\) est une fonction polynomiale de degré inférieur ou égal à \(n-1\) (\(n \geq 1\)).

  2. Montrer que \(f\) est de classe \(\mathcal C ^\infty\) en \(0_{+}\).

  3. Montrer que le polynôme \(P_n\) possède \(n-1\) racines dans \(\mathbb{R}^{+*}\).


[ID: 3460] [Date de publication: 12 mars 2024 09:54] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

\((1+1/t)^t\) **

12 mars 2024 09:54 — Par Michel Quercia

  1. Montrer que : \(\forall t > 1\), \(\left(1+\dfrac 1t\right)^t < e < \left(1+\dfrac 1{t-1}\right)^t\).

  2. Montrer que : \(\forall x,y>0\), \(\left(1+\dfrac xy\right)^y < e^x < \left(1+\dfrac xy\right)^{x+y}\).


[ID: 3461] [Date de publication: 12 mars 2024 09:54] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

\((1+1/t)^t\)
Par Michel Quercia le 12 mars 2024 09:54

  1. Étudier les logs.

  2. Idem.


\(\ln(1+ax)/\ln(1+bx)\) **

12 mars 2024 09:54 — Par Michel Quercia

Soient \(0 < a < b\). Montrer que la fonction \(f : \mathbb{R}^{+*} \rightarrow \mathbb{R}, x \mapsto \dfrac {\ln(1+ax)}{\ln(1+bx)}\) est croissante.


[ID: 3463] [Date de publication: 12 mars 2024 09:54] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

\(\ln(1+ax)/\ln(1+bx)\)
Par Michel Quercia le 12 mars 2024 09:54

\(\dfrac{f'(x)}{f(x)} = \dfrac a{(1+ax)\ln(1+ax)} - \dfrac b{(1+bx)\ln(1+bx)}\). Pour \(x \geq 0\) fixé, la fonction \(t\mapsto \dfrac t{(1+tx)\ln(1+tx)}\) est décroissante.


Inégalité **

12 mars 2024 09:54 — Par Michel Quercia

Soient \(0 < a < b\). Montrer que : \(\forall x > 0\), \(ae^{-bx} - be^{-ax} > a-b\).


[ID: 3465] [Date de publication: 12 mars 2024 09:54] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Racine d’une somme d’exponentielles **

12 mars 2024 09:54 — Par Michel Quercia

Soient \(0 < a_{1} < a_{2} < \dots< a_p\) des réels fixés.

  1. Montrer que pour tout réel \(a > a_p\) il existe un unique réel \(x_a > 0\) solution de : \(a_{1}^x + \dots+ a_p^x = a^x\).

  2. Pour \(a < b\), comparer \(x_a\) et \(x_b\).

  3. Chercher \(\lim_{a\to +\infty } x_a\) puis \(\lim_{a\to +\infty } x_a\ln a\).


[ID: 3466] [Date de publication: 12 mars 2024 09:54] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Racine d’une somme d’exponentielles
Par Michel Quercia le 12 mars 2024 09:54

  1. Étude de \(x\mapsto \left(\dfrac{a_{1}}a\right)^x + \dots+ \left(\dfrac{a_p}a\right)^x\).

  2. \(x_a > x_b\).

  3. \(x_a\to l\). Si \(l > 0\), \(a^{x_a} \to +\infty\), mais \(a_{1}^{x_a} + \dots+ a_p^{x_a} \to a_{1}^l + \dots+ a_p^l\). Donc \(l = 0\), et \(x_a\ln a \to \ln p\).


Centrale MP 2000 ** Centrales MP

12 mars 2024 10:02 — Par Michel Quercia

Soit \(f:\mathbb{R}^{+*}\to \mathbb{R}^{+*}\) telle que : \(\forall x,y>0\), \(f(xf(y))=yf(x)\) et \(f(x)\xrightarrow[x\rightarrow 0_{+} ]{}+\infty\).

  1. Montrer que \(f\) est involutive.

  2. Montrer que \(f\) conserve le produit. Que peut-on dire de la monotonie de \(f\), de sa continuité ?

  3. Trouver \(f\).


[ID: 3514] [Date de publication: 12 mars 2024 10:02] [Catégorie(s): Fonctions exponentielles, logarithmes et puissances ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 1 ] [Auteur(s): Michel Quercia ]
Solution

Centrale MP 2000
Par Michel Quercia Emmanuel Vieillard-Baron le 12 mars 2024 10:02

  1. Pour \(x=1\) on a \(f\circ f(y) = yf(1)\) donc \(f\) est injective et pour \(y=1\) : \(f(xf(1))=f(x)\) d’où \(f(1)=1\).

  2. \(f(xy) = f(xf(f(y))) = f(y)f(x)\).

    Pour \(0<x<1\) on a \(f(x^n ) = f(x)^n \xrightarrow[n\rightarrow \infty ]{}+\infty\) donc \(f(x)>1\) ce qui entraîne par morphisme la décroissance de \(f\). Enfin \(f\) est monotone et \(f(]0,+\infty [) = {]0,+\infty [}\) donc \(f\) n’a pas de saut et est continue.

  3. En tant que morphisme continu, \(f\) est de la forme \(x\mapsto x^\alpha\) avec \(\alpha \in \mathbb{R}\) et l’involutivité et la décroissance donnent \(\alpha =-1\).


Les-Mathematiques.net Mathématiques vivantes

Thématiques

;
Success message!