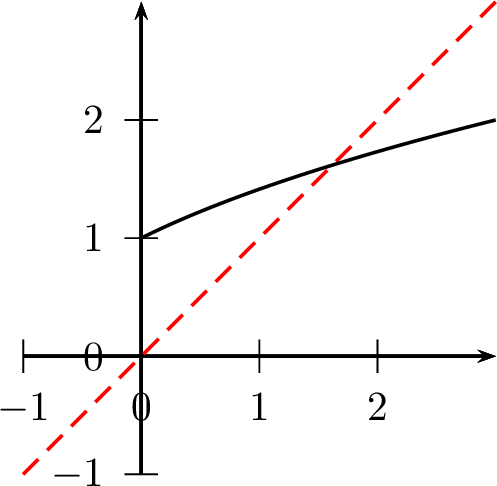Barre utilisateur

[ID: 534] [Date de publication: 12 janvier 2021 15:38] [Catégorie(s): Etude de suites données par une relation de récurrence ] [ Nombre commentaires: 1] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]

Solution(s)

Solution(s)

Exercice 343
Par Emmanuel Vieillard-Baron Alain Soyeur François Capaces le 12 janvier 2021 15:38

On vérifie par récurrence que \(\forall n\in \mathbb N\), \(u_n>0\) et donc que la suite \((u_n)\) est bien définie.

Introduisons la fonction \(f: \left\{ \begin{array}{ccl} \mathbb{R}_+ & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \sqrt{x+1} \end{array} \right.\). Cette fonction est croissante comme composée de fonctions croissantes. Étudions la position de son graphe par rapport à la bissectrice principale. Pour ce faire, considérons la fonction \(g(x)=f(x)-x\), et cherchons son signe. Pour tout \(x\in\mathbb{R}_+\): \[g(x)=\dfrac{ 1+x-x^2}{\sqrt{1+x}+x}=-\dfrac{x^2-x-1}{\sqrt{1+x}+x}\] Notons \(\alpha=\dfrac{1+\sqrt{5}}{2}\). La fonction \(g\) est positive sur \([0,\alpha]\), négative sur \([\alpha,+\infty[\). En particulier, la fonction \(f\) possède un unique point fixe \(\alpha \in [0,+\infty[\).

Les-mathematiques.net

Puisque pour tout \(n\in\mathbb{N}\), \(u_{n+1}-u_n = g(u_n)\), si \(u_n\leqslant\alpha\), \(u_{n+1}\geqslant u_n\) et si \(u_n\geqslant\alpha\), \(u_{n+1}\leqslant u_n\).

On vérifie en utilisant les variations de \(f\) que les intervalles \([0,\alpha]\) et \([\alpha,+\infty[\) sont stables. On étudie alors deux cas :

1. Si \(u_0 \in ]0,\alpha]\), alors pour tout \(n\in \mathbb N\), \(u_n\in[0,\alpha]\) et la suite \((u_n)\) est croissante et majorée par \(\alpha\). Elle converge alors vers l’unique point fixe de \(f\), \(\alpha\).

2. Si \(u_0\in[\alpha,+\infty[\), alors pour tout \(n\in \mathbb N\), \(u_n \in [\alpha,+\infty[\) et la suite \((u_n)\) est décroissante et minorée par \(\alpha\). Elle converge donc vers l’unique point fixe de \(f\), \(\alpha\).

On a donc montré que \(\forall u_0 > 0\), \(\boxed{ u_n\xrightarrow[n \rightarrow +\infty]{}\dfrac{1+\sqrt{5}}{2} }\).