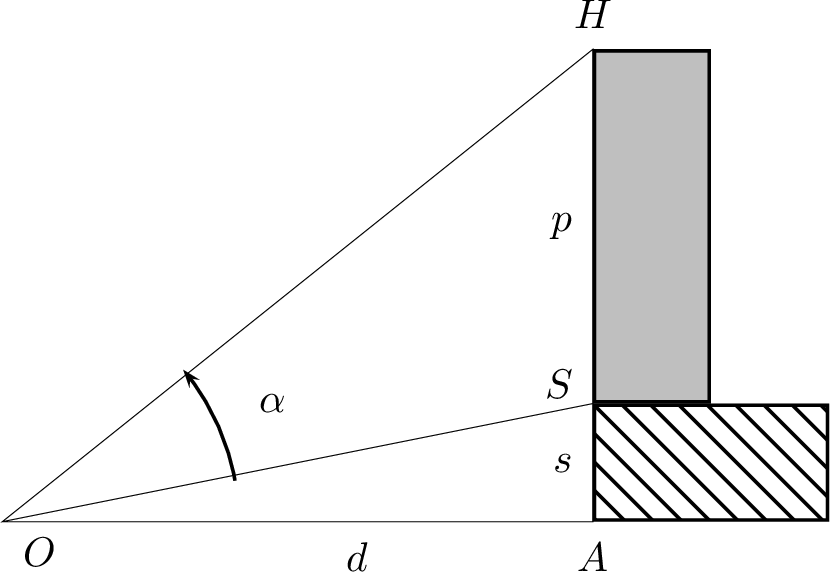Barre utilisateur

[ID: 348] [Date de publication: 11 janvier 2021 15:30] [Catégorie(s): Fonctions circulaires ] [ Nombre commentaires: 1] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): François Capaces Emmanuel Vieillard-Baron Alain Soyeur ]

Solution(s)

Solution(s)

Exercice 8
Par François Capaces Emmanuel Vieillard-Baron Alain Soyeur le 11 janvier 2021 15:30

Notons \(\theta\) l’angle \(\widehat{AOH}\) et \(\varphi\) l’angle \(\widehat{AOS}\). Alors \[\alpha = \theta - \varphi\] Or \(\tan \theta = \dfrac{p+s}{d}\) et \(\tan \varphi= \dfrac{s}{d}\) par conséquent, puisque \(\alpha, \theta, \varphi\in ]0, \dfrac{\pi}{2}[\), \[\alpha = \operatorname{arctan} \dfrac{p+s}{d} - \operatorname{arctan} \dfrac{s}{d}\] En posant \(A = p + s\) et \(B = s\), étudions la fonction \[f: \left\{ \begin{array}{ccl} ]0, +\infty[ & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \operatorname{arctan} \dfrac{A}{x} - \operatorname{arctan} \dfrac{B}{x} \end{array} \right.\] Elle est dérivable sur \(]0, +\infty[\) et \[\forall x\in I, \quad f'(x) = \dfrac{(B-A)(x^2 - AB)}{(x^2+B^2)(x^2+A^2)}\] et donc \(f'\) s’annule en \(x_0 = \sqrt{AB}\) (car \(A > B\), puisque \(s>0\)). On voit sur le tableau de variations de \(f\) que \(x_0\) correspond à un minimum de \(f\) et donc la distance \(d\) sous laquelle on voit la statue sous un angle minimal est : \[d_0 = \sqrt{(p+s)s}\] Cet angle vaut alors \[\alpha_0 = f(d_0) = 2\operatorname{arctan} \left( \sqrt{\dfrac{p+s}{s}}\right) - \dfrac{\pi}{2}\] (on a utilisé la formule \(\operatorname{arctan} x + \operatorname{arctan} \dfrac{1}{x} = \dfrac{\pi}{2}\) lorsque \(x>0\)).