Barre utilisateur

[ID: 330] [Date de publication: 11 janvier 2021 15:29] [Catégorie(s): Fonctions circulaires ] [ Nombre commentaires: 1] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): François Capaces Emmanuel Vieillard-Baron Alain Soyeur ]

Solution(s)

Solution(s)

Exercice 683
Par François Capaces Emmanuel Vieillard-Baron Alain Soyeur le 11 janvier 2021 15:29

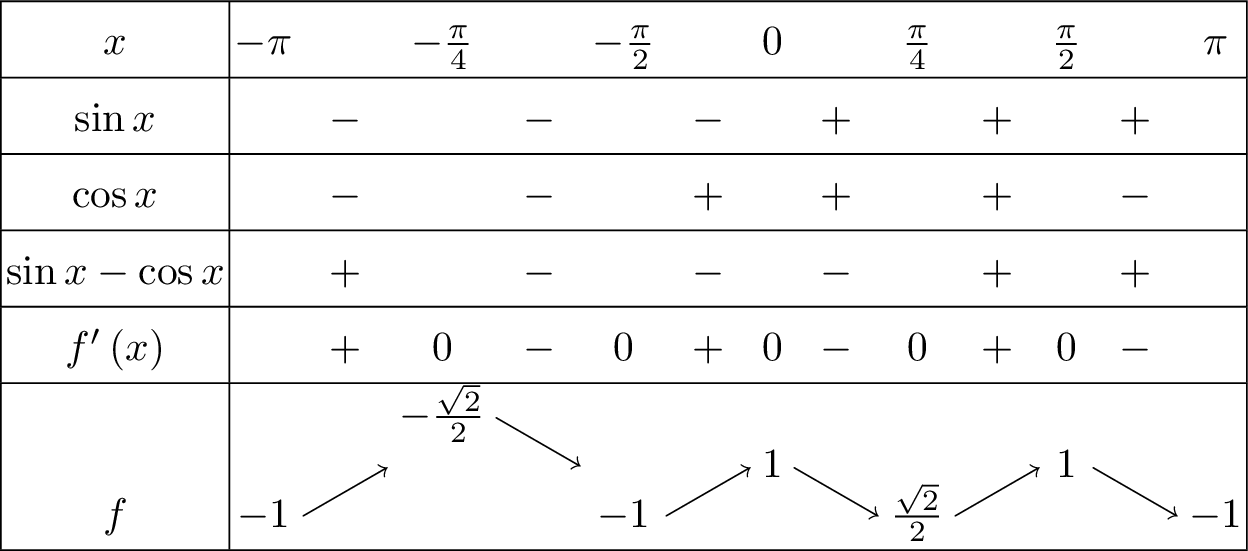
Étudions \(f:x \mapsto \cos^3 x + \sin^3 x\). \(f\) est définie sur \(\mathbb{R}\) mais est \(2\pi\)-périodiques. On peut donc restreindre le domaine d’étude à \(I=\left[-\pi,\pi\right]\). Si \(x\in I\), \(f'\left(x\right)=3\cos x \sin x\left(\sin x - \cos x\right)\). Résolvons l’inéquation  : \(\sin x - \cos x\geqslant 0\) pour \(x\in I\) afin de connaître le signe de \(f\) sur \(I\) : \[\begin{aligned} & & \sin x -\cos x \geqslant 0\\ &\Longleftrightarrow& \dfrac{\sqrt{2}}{2}\cos x- \dfrac{\sqrt{2}}{2}\sin x \leqslant 0\\ &\Longleftrightarrow& \cos\left(x+{\scriptstyle\pi\over\scriptstyle 4}\right) \leqslant 0\\ &\Longleftrightarrow& x\in\left[-\pi,-{\scriptstyle\pi\over\scriptstyle 4 } \right] \cup \left[{\scriptstyle\pi\over\scriptstyle 4},\pi\right]\end{aligned}\] On en déduit le tableau de variation suivant :

Les-mathematiques.net

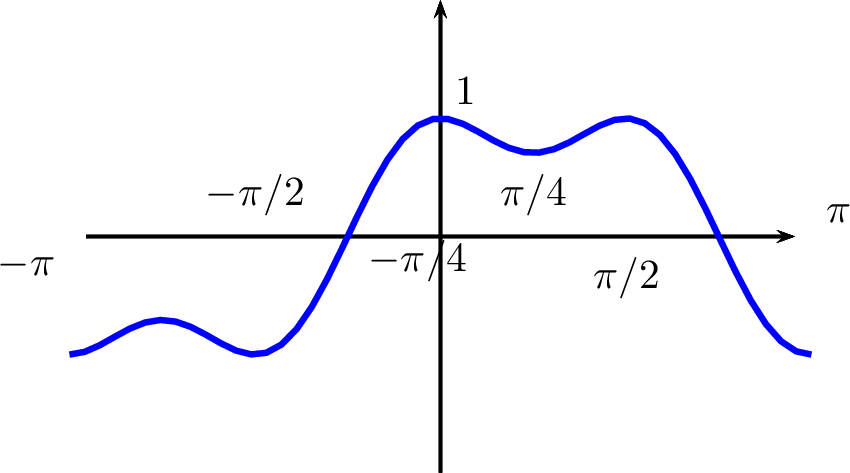
ainsi que le graphe :

Les-mathematiques.net