Lecture zen
**
Exercice 302
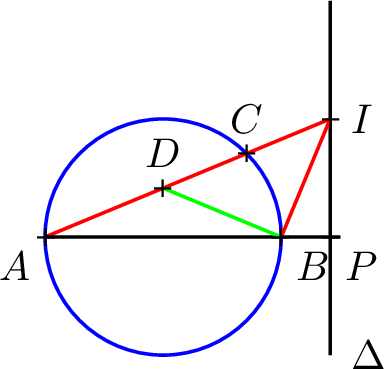
On considère un cercle de centre \(O\) et de rayon \(1\). On considère un diamètre \([AB]\) de ce cercle et un point \(C\) sur le cercle différent de \(A\) et de \(B\) et non situé sur la médiatrice de \([AB]\). On appelle \(D\) le point de la droite \((AC)\) qui se projette orthogonalement sur \((AB)\) en \(O\). La tangente au cercle au point \(C\) coupe la droite \((AB)\) en un point \(P\). Montrer que la droite \((AC)\), la perpendiculaire à \([AB]\) issue de \(P\) et la perpendiculaire à \((BD)\) issue de \(B\) sont concourantes.
Barre utilisateur
[ID: 204] [Date de publication: 4 janvier 2021 18:49] [Catégorie(s): Cercle ] [ Nombre commentaires: 1] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): François Capaces Emmanuel Vieillard-Baron Alain Soyeur ]Solution(s)
Solution(s)
Exercice 302
Par François Capaces Emmanuel Vieillard-Baron Alain Soyeur le 4 janvier 2021 18:49
Par François Capaces Emmanuel Vieillard-Baron Alain Soyeur le 4 janvier 2021 18:49
On considère un repère orthonormal direct centré en \(O\), d’axe \((Ox)\) parallèle à \([AB]\) tel que \(A \underset{}{\left|\begin{matrix} -1\\0 \end{matrix}\right.}\), \(B \underset{}{\left|\begin{matrix} 1\\0 \end{matrix}\right.}\). Il existe \(\theta\in\mathbb{R}\) tel que \(C \underset{}{\left|\begin{matrix} \cos\theta \\ \sin\theta \end{matrix}\right.}\). Comme \(C\) n’est pas situé sur la médiatrice de \([AB]\), \(\cos \theta\neq 0\). On calcule une équation cartésienne de la droite \((AC)\) dans ce repère et on trouve : \[\boxed{ (AC)~: \sin\theta x - (\cos\theta + 1)y + \sin\theta = 0 }\] Puis on calcule les coordonnées de \(\boxed{D \underset{}{\left|\begin{matrix} 0\\ \tan\theta/2 \end{matrix}\right.}}\). La tangente en \(C\) au cercle a pour équation cartésienne \[\boxed{ T_{\theta}:~ \cos \theta x + \sin\theta y = 1 }\] et on trouve les coordonnées du point \(P\) :\(\boxed{P \underset{}{\left|\begin{matrix} 1/\cos\theta \\ 0 \end{matrix}\right.}}\). On note \(I\) l’intersection de la perpendiculaire à \((BD)\) passant par \(B\) et de la perpendiculaire à \((AB)\) passant par \(P\) : \(I = B + \lambda \overrightarrow{n}\) où \(\overrightarrow{n} \underset{}{\left|\begin{matrix} \tan\theta/2 \\ 1 \end{matrix}\right.}\) est orthogonal au vecteur \(\overrightarrow{BD}\). En utilisant que \(x_I = 1/\cos\theta\), on trouve que \[\boxed{ I \underset{}{\left|\begin{matrix} 1/\cos\theta \\ \tan \theta \end{matrix}\right.} }\] Il ne reste plus qu’à vérifier que ce point appartient à la droite \((AC)\) : \[\dfrac{\sin\theta}{\cos\theta} - (\cos\theta + 1)\dfrac{\sin\theta}{ \cos\theta} + \sin \theta = 0\]
Documents à télécharger
L'exercice