Lecture zen
**
Exercice 338
On considère dans le plan un cercle de centre \(\Omega\) et de rayon \(R\). Soit \(M\) un point du plan. On appelle puissance de \(M\) par rapport au cercle \(C\), le réel \[\pi_C(M) = \lVert \overrightarrow{\Omega M} \rVert_{ }^2 - R^2\]
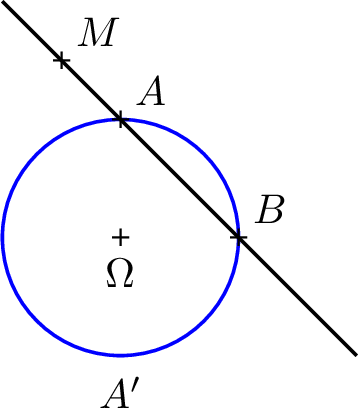
On considère une droite passant par \(M\) et qui coupe le cercle \(C\) en deux points \(A\) et \(B\). Montrer que \[\pi_C(M) = \overrightarrow{MA}.\overrightarrow{MB}\]
On considère deux cercles non-concentriques \(C\) et \(C'\) et l’on appelle axe radical l’ensemble des points \(M\) du plan vérifiant \(\pi_C(M) = \pi_C(M')\). Montrer que cet ensemble est une droite orthogonale à la droite joignant les centres des cercles.
Barre utilisateur
[ID: 200] [Date de publication: 4 janvier 2021 18:49] [Catégorie(s): Cercle ] [ Nombre commentaires: 1] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): François Capaces Emmanuel Vieillard-Baron Alain Soyeur ]Solution(s)
Solution(s)
Exercice 338
Par François Capaces Emmanuel Vieillard-Baron Alain Soyeur le 4 janvier 2021 18:49
Par François Capaces Emmanuel Vieillard-Baron Alain Soyeur le 4 janvier 2021 18:49
Introduisons le point \(A'\) symétrique de \(A\) par rapport à \(\Omega\). En utilisant que \([AA']\) est un diamètre, donc que
\(\overrightarrow{BA} . \overrightarrow{BA'} = 0\), calculons \[\begin{aligned} \overrightarrow{MA}.\overrightarrow{MB} &= \overrightarrow{MA}.(\overrightarrow{MA'} + \overrightarrow{A'B}) \\ &= \overrightarrow{MA} . \overrightarrow{MA'} \\ &= (\overrightarrow{M\Omega} + \overrightarrow{\Omega A}) . (\overrightarrow{M\Omega} + \overrightarrow{\Omega A'}) \\ &= \lVert M\Omega \rVert_{ }^2 + \overrightarrow{M\Omega} . (\overrightarrow{\Omega A} + \overrightarrow{\Omega A'}) + \overrightarrow{\Omega A}.\overrightarrow{\Omega A'} \\ &= \lVert M\Omega \rVert_{ }^2 - R^2 \\ &= \pi_{C}(M) \end{aligned}\]
On se place dans un repère orthonormé dans lequel : \[(C):~x^2+y^2=R^2 \quad(C')~:(x-d)^2 + y^2 = r^2\] où \(\Omega \underset{}{\left|\begin{matrix} 0\\0 \end{matrix}\right.}\) et \(\Omega' \underset{}{\left|\begin{matrix} d\\0 \end{matrix}\right.}\) sont les centres des cercles de rayon \(R\) et \(r\). On calcule \[\begin{aligned} \pi_C(M) = \pi_C(M') &\Longleftrightarrow x^2 + y^2 -R^2 = (x-d)^2 + y^2 - r^2 \\ &\Longleftrightarrow 2dx = R^2 + d^2 - r^2 \\ \end{aligned}\] On trouve l’équation d’une droite orthogonale à \((\Omega \Omega')\).
Documents à télécharger
L'exercice