Barre utilisateur

[ID: 2182] [Date de publication: 23 novembre 2021 14:18] [Catégorie(s): Courbes en coordonnées polaires ] [ Nombre commentaires: 1] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]

Solution(s)

Solution(s)

Trifolium
Par Emmanuel Vieillard-Baron Alain Soyeur François Capaces le 23 novembre 2021 14:18

1. Domaine de définition de \(\rho\) : \(\rho\) est définie sur \(\mathbb{R}\).

2. Restriction de l’intervalle d’étude : Soit \(\theta\in\mathbb{R}\).

   • \(\rho(\theta + 2\pi/3) = \rho(\theta)\), donc \(M(\theta + 2\pi/3)\) est l’image du point \(M(\theta)\) par la rotation de centre \(0\) et d’angle \(2\pi /3\). Il suffit de faire l’étude sur un intervalle de la forme \([\alpha, \alpha + 2\pi/3]\) ;

   • \(\rho(\theta + \pi/3) = - \rho(\theta)\), donc le point \(M(\theta + \pi/3)\) est l’image du point \(M(\theta)\) par la rotation d’angle \(-2\pi/3\). Il suffit de faire l’étude sur un intervalle de longueur \(\pi/3\) ;

   • \(\rho(-\theta) = \rho(\theta)\), donc le point \(M(-\theta)\) est le symétrique du point \(M(\theta)\) par rapport à l’axe \(Ox\).

   On fait donc l’étude sur \([0, \pi/6]\), et on complète la courbe par symétrie par rapport à \((0x)\), puis par rotations d’angle \(-2\pi/3\).

3. Variations : La fonction \(\rho\) est décroissante sur \([0, \pi/6]\) et s’annule en \(\pi/6\). Comme \(\rho'\) s’annule en \(0\), la courbe présente une tangente orthoradiale en \(\theta=0\).

4. Points stationnaires : Le passage au pôle est un point ordinaire car \(\rho\) change de signe donc il n’y a pas de point stationnaire.

5. Branches infinies : Il n’y a pas de branche infinie.

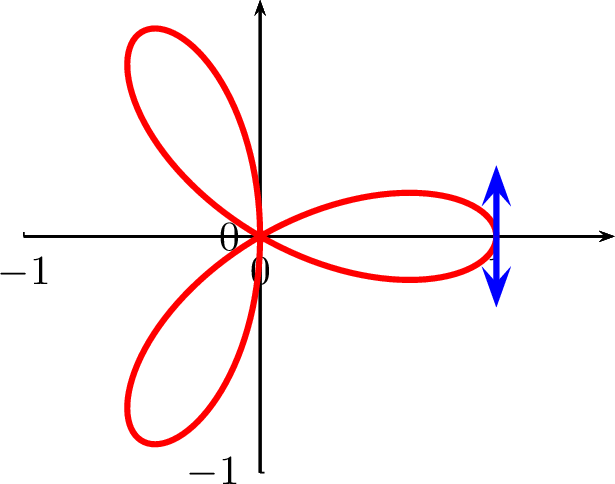
6. Représentation graphique :

   

   Les-mathematiques.net

   Il s’agit d’un trifolium.