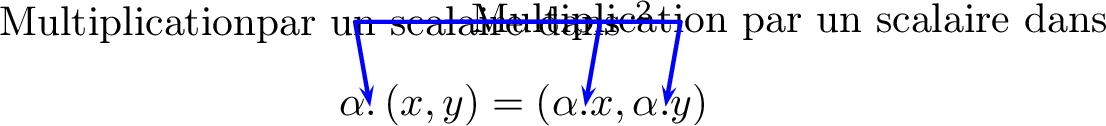La géométrie prédominait dans les mathématiques grecques et il fallut attendre Descartes au \(17^{\textrm{ e}}\) siècle pour faire le lien, grâce à la notion de repère, entre les notions géométriques :
de points du plan ou de l’espace,
de courbes
et celles algébriques
de couples ou de triplets de réels,
d’équations.
Cette approche s’avéra féconde à la fois pour les géomètres et les analystes. Elle offrit aux premiers toute la puissance de l’analyse pour traiter des problèmes de géométrie et, au second, les représentations de la géométrie pour visualiser et énoncer les phénomènes de l’analyse.
La généralisation des notions géométriques du plan \(\mathbb{R}^2\) et de l’espace \(\mathbb{R}^3\) à des espaces de dimension plus grande n’a pas été immédiate. Il manquait le formalisme pour pouvoir aborder ce problème. C’est le mathématicien allemand autodidacte Hermann Grassmann qui, au \(19^{\textrm{ e}}\) siècle, esquissa les notions d’espace vectoriel et de dimension. Son travail était d’un abord difficile et c’est grâce au mathématicien italien Giuseppe Peano que ces concepts se précisèrent et prirent leur forme définitive.
Les mathématiciens disposèrent alors d’outils permettant d’aborder des problèmes de géométrie en dimension quelconque. Cependant c’est l’analyse qui donnera aux espaces vectoriels toute leur importance.
À la fin du \(19^{\textrm{ e}}\) siècle et au début du \(20^{\textrm{ e}}\) siècle, les mathématiciens allemands étudient des espaces de fonctions et créent l’ analyse fonctionnelle. Les espaces étudiés ont des structures d’espace vectoriel. Le mathématicien polonais Stefan Banach écrira, dans sa thèse, que plutôt que d’étudier des problèmes particuliers et de démontrer isolément leurs propriétés, une meilleure stratégie est de prouver ces propriétés pour des ensembles généraux pour lesquels on a postulé des propriétés, puis de montrer que ces axiomes sont vérifiés par les problèmes particuliers.
Cette approche fonde en quelque sorte les mathématiques modernes. On introduit et étudie dans un premier temps des structures (groupe, anneau, corps, espace vectoriel, ...) puis on vérifie à quelle catégorie se rattache un exemple particulier donné. Il hérite alors de toutes les propriétés de la catégorie à laquelle il appartient.
Les premiers pas en algèbre linéaire sont en général difficiles et rebutants. La difficulté ne tient pas tellement, contrairement à ce qu’on pourrait penser, à la difficulté des raisonnements mathématiques ou à l’abstraction des notions utilisées. Elle réside plutôt dans le caractère nouveau de ces raisonnements et de ces notions. Un conseil, ne vous laissez pas impressionner, ne vous braquez pas. Le temps et le travail aidant, vous allez vite comprendre dans quel nouvel endroit vous avez mis les pieds et, passé la phase de découverte, vous allez vite vous sentir en sécurité. Les chapitres [geom_plan] et [geom_espace] de géométrie dans le plan et dans l’espace vont vous être d’un grand secours car ils vous aideront à vous forger des représentations et ils guideront votre intuition.
Espace vectoriel
Dans tout ce chapitre \(\mathbb{K}\) désigne le corps \(\mathbb{R}\) ou \(\mathbb{C}\).
Définitions
Nous allons donner les axiomes qui définissent un espace vectoriel.
(\(\mathbb{K}\)-espace vectoriel). Soit \(\left(\mathbb{K},+,\times\right)\) un corps. On appelle espace vectoriel sur le corps \(\mathbb{K}\) tout ensemble \(E\) muni d’une loi de composition interne \(+\) (addition) \[+: \left\{ \begin{array}{ccl} E\times E & \longrightarrow & E \\ \left(x,y\right) & \longmapsto & x+y \end{array} \right.\] et d’une loi de composition externe \(\cdot\) (multiplication par un scalaire) \[\cdot: \left\{ \begin{array}{ccl} \mathbb{K}\times E & \longrightarrow & E \newline \left(\lambda,x\right) & \longmapsto & \lambda\cdot x \end{array} \right.\] telles que
\(\left(E,+\right)\) est un groupe commutatif. On note \(0_E\) son élément neutre.
Pour tout \(\left(\alpha,\beta\right) \in \mathbb{K}^2\) et pour tout \(\left(x,y\right)\in
E^2\), on a
\(\alpha\cdot\left(x+y\right)=\alpha\cdot x + \alpha\cdot y\)
\(1_{\mathbb{K}}\cdot x = x\)
On dit alors que \(\left(E,+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel. Les éléments de \(\mathbb{K}\) sont appelés scalaires, ceux de \(E\), vecteurs. L’élément neutre de \(\left(E,+\right)\), \(0_E\) est appelé vecteur nul.
On vous avait prévenu, cela peut sembler abstrait... Cela ne l’est en fait pas tant que ça. Un espace vectoriel est un ensemble sur lequel on peut définir une addition et une multiplication par un scalaire et rien de plus, si ce n’est que cette addition et cette multiplication doivent vérifier les axiomes ci-dessus. Vous connaissez un certain nombre d’ensembles de ce type :
\(\mathbb{R}\) (\(\mathbb{K}=\mathbb{R}\)) et \(\mathbb{C}\) (\(\mathbb{K}=\mathbb{R}\) ou \(\mathbb{C}\)).
L’ensemble des vecteurs du plans (\(\mathbb{K}=\mathbb{R}\)).
L’ensemble des vecteurs de l’espace (\(\mathbb{K}=\mathbb{R}\)).
Les ensembles \(\mathbb{R}^2\) et \(\mathbb{R}^3\) (\(\mathbb{K}=\mathbb{R}\)).
L’ensemble des suites réelles \(\mathcal S\left(\mathbb{R}\right)\) (\(\mathbb{K}=\mathbb{R}\)) ou complexes \(\mathcal
S\left(\mathbb{C}\right)\) (\(\mathbb{K}=\mathbb{R}\) ou \(\mathbb{C}\)).
L’ensemble \(\mathcal F\left(I,\mathbb{R}\right)\) des fonctions de \(I\) dans \(\mathbb{R}\) (\(\mathbb{K}=\mathbb{R}\)) (ou dans \(\mathbb{C}\) (\(\mathbb{K}=\mathbb{R}\))) où \(I\) est un intervalle de \(\mathbb{R}\).
Les ensembles de polynômes \(\mathbb{R}\left[X\right]\) (\(\mathbb{K}=\mathbb{R}\)) et \(\mathbb{C}\left[X\right]\) (\(\mathbb{K}=\mathbb{R}\) ou \(\mathbb{C}\)).
L’ensemble \(\mathbb{K}_n\left[X\right]\) des polynômes de degré \(\leqslant n\) à coefficients dans \(\mathbb{K}\) où \(n\in\mathbb{N}\).
Nous allons formaliser cette remarque dans la prochaine section.
Prenons tout de suite de bonnes habitudes. Il est essentiel de bien distinguer les notions vectorielles des notions affines. Les espaces affines sont ceux que vous connaissez depuis le collège. Dans un espace affine :
Un vecteur est donné par deux points, un point de départ \(A\) et un point d’arrivée \(B\). On dit que deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{CD}\) sont égaux si \(ABDC\) est un parallélogramme.
Une droite est composée de points. Elle est donnée par un point par lequel elle passe et par un vecteur qui la dirige. On parle de droite affine (Voir la définition dans le chapitre [geom_plan]).
Un plan est lui aussi composé de points. Il est donné par un point par lequel il passe et par deux vecteurs qui l’engendrent. On parle de plan affine (Voir la définition dans le chapitre [geom_espace]).
Si on fixe une origine \(O\) dans notre espace affine, ses points peuvent être identifiés aux vecteurs d’origine \(O\). Ce sont ces vecteurs qui nous intéressent dans un espace vectoriel. La notion de point n’a pas de sens. Dans un espace vectoriel :
Tous les éléments sont des vecteurs. On peut se les représenter comme les vecteurs d’origine \(O\) d’un espace affine.
Une droite est engendrée par un vecteur u (non nul) et est formée de vecteurs. On peut se l’imaginer dans un espace affine comme une droite passant par \(O\) et dirigée par u.
Un plan est engendré par deux vecteurs u et v (non colinéaires) et est formé de vecteurs. On peut se l’imaginer dans un espace affine comme un plan passant par \(O\) et engendré par u et v.
Autant il est utile parfois de se représenter certaines notions d’algèbre linéaire dans le plan ou dans l’espace, autant parfois ceci est impossible...Cela n’est en général pas gênant...
Espaces produits
Soit \(\left(\mathbb{K},+,\cdot\right)\) un corps. Alors \(\left(\mathbb{K},+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel.
L’addition dans \(\mathbb{K}\) est une loi interne sur \(\mathbb{K}\) et la multiplication sur \(\mathbb{K}\) peut être vue comme une loi externe. On vérifie facilement que ces deux lois vérifient les axiomes définissant un \(\mathbb{K}\)-espace vectoriel.
On va munir l’ensemble des couples de réels \(\mathbb{R}^2\) d’une structure de \(\mathbb{R}\)-espace vectoriel. On définit une addition et une multiplication par un scalaire ainsi. Pour tous \(\left(x,y\right),\left(x',y'\right)\in\mathbb{R}^2\) et tout \(\alpha\in\mathbb{R}\), on pose : \[\left(x,y\right)+\left(x',y'\right)=\left(x+x',y+y'\right) \quad \textrm{ et} \quad\alpha.\left(x,y\right)=\left(\alpha x,\alpha y\right)\] On vérifie (c’est un peu long et laborieux mais c’est facile) que ces deux lois vérifient les axiomes définissant un \(\mathbb{R}\)-espace vectoriel. Attention, le vecteur nul de cet espace est donné par \(0_{\mathbb{R}^2}=\left(0,0\right)\).
Attention au sens des opérations \(+\) et \(.\) dans les définitions ci-dessus :
Les-mathematiques.net
Les-mathematiques.net
On généralise cette construction ainsi :
(Espace vectoriel \(\mathbb{K}^n\)). Sur l’ensemble des \(n\)-uplets de scalaires \(\mathbb{K} [n]\), on définit
une multiplication par un scalaire \(\cdot\)\[\cdot: \left\{ \begin{array}{ccl} \mathbb{K}\times\mathbb{K}^n & \longrightarrow & \mathbb{K}^n \newline \left(\alpha,\left(x_1,\ldots,x_n\right)\right) & \longmapsto & \left(\alpha x_1,\ldots,\alpha x_n\right) \end{array} \right.\]
Muni de ces lois, l’ensemble \(\left(\mathbb{K}^n,+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel. Son vecteur nul est le n-uplet \(\boxed{0_{\mathbb{K} [n]} = \left(0,\ldots,0\right)}\).
Vérifications faciles.
Un corollaire immédiat est alors le suivant :
(Espaces vectoriels \(\mathbb{R}^n\) et \(\mathbb{C}^n\)).
Le triplet \(\left(\mathbb{R}^n,+,\cdot\right)\) est un \(\mathbb{R}\)-espace vectoriel.
Le triplet \(\left(\mathbb{C}^n,+,\cdot\right)\) est un \(\mathbb{R}\)-espace vectoriel.
En particulier, \(\mathbb{R}\) et \(\mathbb{C}\) sont des \(\mathbb{R}\)-espaces vectoriels.
De manière plus générale, on a :
(Produit d’espaces vectoriels). Soient \(\left(E_1,+,\cdot\right)\) et \(\left(E_2,+,\cdot\right)\) deux \(\mathbb{K}\)-espaces vectoriels. On définit sur l’ensemble \(E_1\times E_2\)
une multiplication par un scalaire \(\cdot\)\[\cdot: \left\{ \begin{array}{ccl} \mathbb{K}\times \left(E_1\times E_2\right) & \longrightarrow & E_1\times
E_2 \newline \left(\alpha,\left(x_1,x_2\right) \right) & \longmapsto & \left(\alpha\cdot x_1,\alpha\cdot
x_2\right) \end{array} \right. .\]
Alors \(\left(E_1\times E_2,+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel. Son vecteur nul est \(\boxed{\left(0_{E_1},0_{E_2}\right)}\).
Vérifications faciles.
Espaces de suites et de fonctions
Comme précisé dans l’introduction, on peut munir certains espaces de fonctions de structure d’espace vectoriel. Il suffit pour cela que les fonctions soient à valeurs dans un espace vectoriel.
(Espace vectoriel de fonctions). Soit \(X\) un ensemble non vide et soit \(E\) un \(\mathbb{K}\)-espace vectoriel. On définit sur l’ensemble \(\mathcal F\left(X,E\right)\) des fonctions définies sur \(X\) à valeurs dans \(E\)
une multiplication par un scalaire \(\cdot\)\[\cdot: \left\{ \begin{array}{ccl} \mathbb{K}\times\mathcal F\left(X,E\right) & \longrightarrow & \mathcal F\left(X,E\right) \\ \left(\alpha,f\right) & \longmapsto & \alpha \cdot f \end{array} \right.\] donnée par \(\forall x\in X, \quad\left(\alpha\cdot f\right)\left(x\right)=\alpha
f\left(x\right)\)
Muni de ces lois, l’ensemble \(\left(\mathcal{F}\left(X,E\right),+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel. Son vecteur nul est la fonction identiquement nulle sur \(X\) à valeurs dans \(E\) : \(\boxed{0_{\mathcal{F}\left(X, E\right)} : \left\{ \begin{array}{ccl} X & \longrightarrow & E \newline x & \longmapsto & 0_E \end{array} \right. }\)
Les vérifications sont immédiates.
Attention au sens des opérations \(+\) et \(.\) dans les définitions ci-dessus :
Les-mathematiques.net
Les-mathematiques.net
En appliquant ce résultat avec \(X=\mathbb{N}\) et \(E=\mathbb{K}\), on obtient :
(Suites à coefficients dans \(\mathbb{K}\)). Notons \(\mathscr S\left(\mathbb{K}\right)\) l’ensemble des suites à coefficients dans \(\mathbb{K}\). Avec les lois \[+: \left\{ \begin{array}{ccl} \mathscr S\left(\mathbb{K}\right)\times\mathscr S\left(\mathbb{K}\right) & \longrightarrow & \mathscr
S\left(\mathbb{K}\right) \\ \left(\left(u_n\right),\left(v_n\right)\right) & \longmapsto & \left(u_n+v_n\right) \end{array} \right.\]\[\cdot: \left\{ \begin{array}{ccl} \mathbb{K}\times\mathscr S\left(\mathbb{K}\right) & \longrightarrow & \mathscr
S\left(\mathbb{K}\right) \newline \left(\lambda,\left(u_n\right)\right) & \longmapsto & \left(\lambda\cdot u_n\right) \end{array} \right.\]\(\left(\mathscr S\left(\mathbb{K}\right),+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel. Son vecteur nul est la suite constante nulle.
Règles de calcul dans un espace vectoriel
Les quatre axiomes donnés dans la définition [def_K_ev] ne traduisent à priori pas toutes les règles de calculs qu’on est habitué à utiliser quand on manipule des vecteurs. On va montrer que ces règles découlent bien de ces quatre axiomes.
(Règles de calcul dans un espace vectoriel). Soit \(\left(E,+,\cdot\right)\) un \(\mathbb{K}\)-espace vectoriel. Pour tous scalaires \(\alpha,\beta,\lambda
\in \mathbb{K}\) et pour tous vecteurs \(x,y\in E\), on a
Les démonstrations de ces règles vous sembleront sans doute un peu arides dans un premier temps. Il est important de bien les travailler jusqu’à être capable de les refaire seul.
\[\begin{aligned}
O_E+0_{K}x&=&0_{K}x \textrm{ car $\left(E,+\right)$ est un groupe}\\
&=&\left(0_K + 0_K\right)x \textrm{ car $\mathbb{K}$ est un corps}\\
&=&0_K x + 0_K x \textrm{ d'après l'axiome ~4~
}
\end{aligned}\] D’où \(0_{\mathbb{K}}\cdot x=0_E\) en soustrayant \(0_K x\) à droite des deux membres de cette égalité.
On a : \[\begin{aligned}
x+\left(-1\right)x &=& 1.x+\left(-1\right)x \textrm{ grâce à l'axiome ~4}\\
&=& \left(1+\left(-1\right)\right)x \textrm{ grâce à l'axiome ~1~}\\
&=& 0_K x \textrm{ car $\mathbb{K}$ est un corps}\\
&=& 0_E \textrm{ d'après le point précédent}
\end{aligned}\] donc \(\left(-1\right)x\) est l’opposé de \(x\). On peut alors écrire : \(-x=\left(-1\right)x\).
on a : \[\begin{aligned}
\left(-\lambda \right)x&=& \left(-1 . \lambda \right)x \textrm{ car $\mathbb{K}$ est un corps}\\
&=& \left(-1\right)\left(\lambda x\right) \textrm{ d'après l'axiome ~2~}\\
&=& -\lambda .x \textrm{ d'après le point précédent}\\
\end{aligned}\]
\[\begin{aligned}
\left(\alpha - \beta \right) x &=& \left(\alpha + \left(-\beta\right)\right) x \textrm{ car $\mathbb{K}$ est un
corps}\\
&=& \alpha x+\left(-\beta x\right) \textrm{ d'après l'axiome ~1~}\\
&=& \alpha x - \beta x \textrm{ d'après le point précédent}
\end{aligned}\]
\[\begin{aligned}
\lambda\left(x-y\right)&=&\lambda\left(x+\left(-y\right)\right) \textrm{ car $\left(E,+\right)$ est un groupe}\\
&=& \lambda x + \lambda \left(- y\right) \textrm{ d'après l'axiome ~3~ }\\
&=& \lambda x + \lambda \left(-1 y\right) \textrm{ d'après le second point}\\
&=& \lambda x + \left(\lambda.\left(-1\right)\right)y \textrm{ d'après l'axiome
~2~}\\
&=& \lambda x +\left(-\lambda \right)y \textrm{ car $\mathbb{K}$ est un corps}\\
&=& \lambda x - \lambda y \textrm{ d'après le point $3$}
\end{aligned}\]
\[\begin{aligned}
\lambda 0_E&=&\lambda\left(x-x\right) \textrm{ car $\left(E,+\right)$ est un groupe}\\
&=& \lambda x + \lambda\left(-x\right) \textrm{ d'après l'axiome ~1~}\\
&=& \lambda x -\lambda x \textrm{ d'après le point $3$}\newline
&=& 0_E \textrm{ car $\left(E,+\right)$ est un groupe}
\end{aligned}\]
Supposons que \(\lambda x = 0_E\). Si \(\lambda=0_K\) alors d’après le point \(1\), \(\lambda x=0_E\). Sinon, si \(\lambda\neq 0_K\) alors comme \(\mathbb{K}\) est un corps, \(\lambda^{-1}\) existe et \[x=1.x=\left(\lambda.\lambda^{-1}\right)x=\lambda^{-1}\left(\lambda
x\right)=\lambda^{-1}0_E=0_E\] et donc \(x=0_E\). La réciproque est évidente.
Sous-espace vectoriel
Définitions
(Combinaison linéaire).
Soient \(x_1,\dots,x_n\)\(n\) vecteurs d’un \(\mathbb{K}\)-espace vectoriel \(\left(E,+,.\right)\). On appelle combinaison linéaire de ces \(n\) vecteurs tout vecteur \(x\in E\) de la forme \[\displaystyle{x=\lambda_1\cdot x_1+ \dots+ \lambda_n \cdot x_n =
\sum_{k=0}^{n} \lambda_k \cdot x_k}\] où \(\left(\lambda_1,\dots,\lambda_n\right)\in\mathbb{K}^n\).
Si \(A\) est une partie de \(E\), on appelle combinaison linéaire d’éléments de \(A\) toute combinaison linéaire d’un nombre fini d’éléments de \(A\).
On montre par une récurrence facile qu’une combinaison linéaire de vecteurs de \(E\) est encore un vecteur de \(E\).
Soit \(f: \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \cos x + 2\sin x \end{array} \right.\). C’est une combinaison linéaire des deux fonctions \(\cos\) et \(\sin\) de \(\mathcal{F}\left(\mathbb{R} , \mathbb{R} \right)\) et c’est un encore un élément de \(\mathcal{F}\left(\mathbb{R} , \mathbb{R} \right)\).
Soient \(u=\left(1,2\right)\) et \(v=\left(-1,1\right)\) deux éléments de \(\mathbb{R}^2\). Alors la combinaison linéaire \(2u-3v=2\left(1,2\right)-3\left(-1,1\right)=\left(5,1\right)\) est encore un élément de \(\mathbb{R}^2\).
Soit \(\omega>0\). L’ensemble des solutions de l’équation différentielle : \(y''+\omega y=0\) est l’ensemble de toutes les combinaisons linéaires possibles des fonctions \(\varphi_1: \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \cos \left(\omega x\right) \end{array} \right.\) et \(\varphi_2: \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \newline x & \longmapsto & \sin \left(\omega x\right) \end{array} \right.\).
(Sous-espace vectoriel). Soient \(\left(E,+,.\right)\) un \(\mathbb{K}\)-espace vectoriel et \(F\subset E\), une partie de \(E\). On dit que \(F\) est un sous-espace vectoriel de \(E\) si et seulement si
La partie \(F\) est non vide : \(F\neq \varnothing\),
la partie \(F\) vérifie : \[\forall \left(x,y\right)\in E^2, \quad \forall \left(\alpha,\beta\right)\in \mathbb{K}^2,
\quad \alpha\cdot x + \beta \cdot y \in F\]
Si \(F\) est un sous-espace vectoriel de \(E\) alors \(0_E\in F\). En effet, comme \(F\) est non vide, il existe \(x\in F\). Comme \(F\) est un sous-espace vectoriel, alors \(x-x=1.x-1.x=0_E\in F\).
En partant de second axiome de la définition d’un sous-espace vectoriel et au moyen d’une récurrence, on montre sans peine que \(F\) est stable par combinaison linéaire, c’est-à-dire que toute combinaison linéaire de vecteurs de \(F\) est encore un vecteur de \(F\).
Dans tout espace vectoriel \(E\), il y a toujours deux sous-espaces vectoriels importants, \(F = \{0_E\}\) et \(F = E\).
Dans l’idée de faire le parallèle avec les groupes, on aurait pu définir la notion de sous-espace vectoriel de la façon suivante : \(F\) est un sous-espace vectoriel de \(E\) si et seulement si \(F\) est un sous-groupe de \(E\) stable pour la multiplication par tout scalaire.
(Pour montrer que \(F\) est un sous-espace vectoriel de \(E\)).
On montre que \(F\subset E\).
On montre que \(F \neq \varnothing\) (la plupart du temps on montre que \(0\in A\)).
Soit \(\left(\alpha,\beta\right)\in \mathbb{K}^2\) et soit \(\left(x,y\right)\in F^2\). Montrons que \(\alpha\cdot x + \beta \cdot y \in F\).
On étudiera avec attention les exemples suivants :
L’ensemble des nombres réels \(\mathbb{R}\) est un sous-espace vectoriel du \(\mathbb{R}\)-espace vectoriel \(\mathbb{C}\). De même, l’ensemble des nombres imaginaires purs \(i\mathbb{R}\) est un sous-espace vectoriel de \(\mathbb{C}\). En effet :
\(i\mathbb{R}\subset \mathbb{C}\).
\(i\mathbb{R}\) est non vide...
Si \(\alpha,\beta\in\mathbb{R}\) et si \(ix,iy\in i\mathbb{R}\) alors \(\alpha ix+ \beta
iy=i\underbrace{\left(\alpha x + \beta y\right)}_{\in\mathbb{R}} \in i\mathbb{R}\).
Soit \(u\) un vecteur non nul du plan (ou de l’espace). L’ensemble \(F\) de tous les vecteurs du plan colinéaires à \(\overrightarrow{u}\), \(F=\left\{\lambda \overrightarrow{u} ~|~ \lambda \in\mathbb{R}\right\}\) est un sous-espace vectoriel du plan (ou de l’espace). C’est la droite vectorielle dirigée par \(\overrightarrow{u}\) :
Il est clair que \(F\) est un sous-ensemble du plan (ou de l’espace).
\(F\) est non vide, il contient par exemple \(u\).
Si \(\alpha,\beta\in\mathbb{R}\) et si \(\lambda u,\lambda' u\in F\) alors \(\alpha
\left(\lambda u\right)+\beta \left(\lambda' u\right)=\left(\alpha \lambda+\beta \lambda'\right)u\in F\).
Soient \(u\) et \(v\) deux vecteurs non colinéaires de l’espace. L’ensemble \(F\) de toutes les combinaisons linéaires de \(u\) et \(v\), \(F=\left\{\alpha u + \beta v~|~ \alpha,\beta
\in\mathbb{R}\right\}\) est un sous-espace vectoriel de l’espace :
Il est clair que \(F\) est un sous-ensemble de l’espace.
\(F\) est non vide, il contient \(u\), \(v\),...
Si \(\alpha,\beta\in \mathbb{R}\) et si \(au+bv, a'u+b'v\in F\) alors \(\alpha
\left(au+bv\right)+\beta\left(a'u+b'v\right)=\left(a\alpha+a'\beta\right)u+\left(b\alpha+b'\beta\right)v\in F\).
Si ces deux vecteurs ne sont pas colinéaires, \(F\) est le plan vectoriel engendré par \(u\) et \(v\).
L’ensemble des triplets \(\left(x,y,z\right)\) de \(\mathbb{R}^3\) solutions de \(2x+y-z=0\) est un sous espace vectoriel de \(\mathbb{R}^3\) :
Il est clair que \(F\subset \mathbb{R}^3\).
\(F\) est non vide, le triplet \(\left(0,0,0\right)\) est solution de \(2x+y-z=0\).
Si \(\alpha,\beta\in\mathbb{R}\) et si \(u=\left(x,y,z\right),\left(x',y',z'\right)\in\mathbb{R}^3\) alors \(\alpha\left(x,y,z\right)+\beta\left(x',y',z'\right)\) est élément de \(F\). En effet \(u=\left(\alpha
x+ \beta x',\alpha
y+ \beta y',\alpha
z+ \beta z'\right)\) et \[2\left(\alpha
x+ \beta x'\right) + \left(\alpha
y+ \beta y'\right)-\left(\alpha
z+ \beta z'\right)=\alpha\underbrace{\left(2x+y-z\right)}_{=0 \textrm{ car }\left(x,y,z\right)\in
F}+\beta \underbrace{\left(2x'+y'-z'\right)}_{=0 \textrm{ car }\left(x',y',z'\right)\in F}=0.\] On remarque que \(F\) est un plan vectoriel.
L’ensemble \(F=\mathcal{C}^{0}\left(\mathbb{R}\right)\) des fonctions continues de \(\mathbb{R}\) dans \(\mathbb{R}\) est un sous-espace vectoriel de \(E=\mathscr F\left(\mathbb{R},\mathbb{R}\right)\). En effet :
Il est clair que \(F\subset E\).
Il existe des fonctions continues sur \(\mathbb{R}\) (\(\cos, \sin,\exp\),...) donc \(F\) est non vide.
Si \(\alpha,\beta\in\mathbb{R}\) et si \(f,g\in \mathcal{C}^{0}\left(\mathbb{R}\right)\) alors par le théorème d’opération sur les fonctions continues, \(\alpha f + \beta g\) est encore continue sur \(\mathbb{R}\). Donc \(F\) est stable par combinaison linéaire.
On montre de la même façon que pour tout \(n\in\mathbb{N}\), les ensembles \(\mathcal{C}^{n}\left(\mathbb{R}\right)\) sont des sous-espaces vectoriels de \(\mathscr F\left(\mathbb{R},\mathbb{R}\right)\).
Soit \(F\) l’ensemble des fonctions définies sur \(\left[-1,1\right]\) à valeurs dans \(\mathbb{C}\) qui s’annulent en \(0\). Montrons que \(F\) est un sous-espace vectoriel de \(\left(\mathcal F\left(\left[-1,1\right],\mathbb{C}\right),+,.\right)\).
Il est clair que \(F\subset \mathcal F\left(\left[-1,1\right],\mathbb{C}\right)\).
\(F\) est non vide. Par exemple, la fonction identiquement nulle sur \(\left[-1,1\right]\) est élément de \(F\).
Si \(\alpha,\beta\in\mathbb{C}\) et si \(f,g\in F\) alors \(\left(\alpha f+\beta
g\right)\left(0\right)=\alpha f\left(0\right)+\beta g\left(0\right)=0\) donc \(\alpha f+\beta g\in F\).
En reprenant le troisième item de l’exemple [exemple03/03/201011:46], l’ensemble \(F\) des solutions de \(y''+\omega y=0\) est un sous-espace vectoriel de l’espace vectoriel \(\mathcal{C}^{0}\left(\mathbb{R}\right)\). En effet :
Toute solution de cette équation est (deux fois) dérivable et donc continue. Donc \(F\subset E\).
\(F\) est non vide car l’équation différentielle admet des solutions, par exemple la fonction identiquement nulle sur \(\mathbb{R}\).
Soient \(\alpha,\beta\in\mathbb{R}\) et \(f,g\in F\). Alors \(\left(\alpha f+ \beta
g\right)''+\omega \left(\alpha f+ \beta
g\right)=\alpha\underbrace{\left(f''+\omega f\right)}_{=0 \textrm{ car } f\in F}+ \beta
\underbrace{\left(g''+\omega g\right)}_{=0 \textrm{ car } g\in F}=0\) donc \(\alpha f+ \beta
g\in F\).
L’ensemble \(F=\left\{P\in\mathbb{R}_3\left[X\right]~|~ P\left(1\right)=0\right\}\) est un sous-espace vectoriel de \(\mathbb{R}_3\left[X\right]\). Cela se prouve de la même façon que l’item 6. précédent.
(Pour montrer que \(F\) n’est pas un sous-espace vectoriel de \(E\)). On peut montrer au choix que
\(F\not\subset E\).
\(F =\varnothing\).
\(0_E\not \in F\).
\(F\) n’est pas stable par combinaison linéaire : il existe \(\left(\alpha,\beta\right)\in \mathbb{K}^2\) et \(\left(x,y\right)\in F^2\) tels que \(\alpha\cdot x + \beta \cdot y \not \in F\).
L’ensemble \(F=\left\{f\in \mathcal F\left(\mathbb{R},\mathbb{R}\right)~|~ f\left(0\right)=0\right\}\) n’est pas un sous-espace vectoriel de \(E=\mathcal{C}^{0}\left(\mathbb{R}\right)\) car il existe des fonctions définies sur \(\mathbb{R}\) qui s’annulent en \(0\) et qui ne sont pas continues sur \(\mathbb{R}\).
L’ensemble \(F=\left\{\left(x,y\right)\in R^2~|~ x^2+y^2=-1\right\}\) n’est pas un sous-espace vectoriel de \(\mathbb{R}^2\) car il est vide...
L’ensemble \(F=\left\{f\in \mathcal F\left(\mathbb{R},\mathbb{R}\right)~|~ f\left(0\right)=1\right\}\) n’est pas un sous-espace vectoriel de \(E=\mathcal F\left(\mathbb{R},\mathbb{R}\right)\) car le vecteur nul de \(E\) qui est la fonction identiquement nulle sur \(\mathbb{R}\) n’est pas élément de \(F\).
L’ensemble \(F=\left\{\left(x,y\right)\in\mathbb{R}^2~|~ x^2+y^2 \leqslant 1\right\}\) n’est pas un sous-espace vectoriel de \(\mathbb{R}^2\) car il n’est pas stable par combinaison linéaire : soient \(u=\left(1,0\right)\) et \(v=\left(0,1\right)\). On vérifie facilement que \(u,v\in F\). Par contre \(u+v=\left(1,1\right)\) et \(\left\|u+v\right\|^2=2> 1\) donc \(u+v\not\in F\).
Les-mathematiques.net
(Un sous-espace vectoriel est un espace vectoriel). Soient \(\left(E,+,.\right)\) un \(\mathbb{K}\)-espace vectoriel et \(F\subset E\), une partie non vide de \(E\). On a équivalence entre les deux propositions suivantes.
La partie \(F\) est un sous-espace vectoriel de \(\left(E,+,.\right)\).
Muni des lois de \(E\) restreintes à \(F\), \(\left(F,+,.\right)\) est un \(\mathbb{K}\)-espace vectoriel.
Soient \(\left(x,y\right)\in F^2\) et \(\left(\alpha,\beta\right)\in\mathbb{K}^2\).
On vérifie que \(+\) définit une loi interne sur \(E\), \(x+y=1.x+1.y\in F\) car \(F\) est stable par combinaison linéaire.
De même, \(.\) définit une loi externe sur \(F\). \(\alpha.x=\alpha.x+0.y\in F\) car \(F\) est stable par combinaison linéaire.
Les axiomes d’un espace vectoriel sont vérifiés dans \(F\) car ils sont vérifiés dans \(E\)
La réciproque est facile.
(Pour montrer que \(F\) est un \(\mathbb{K}\)-espace vectoriel...). ... il suffit de montrer que \(F\) est un sous-espace vectoriel d’un \(\mathbb{K}\)-espace vectoriel \(E\) dans lequel il est contenu.
Cette dernière proposition permet d’économiser beaucoup de travail quand on doit montrer qu’un triplet \(\left(F,+,.\right)\) est un \(\mathbb{K}\)-espace vectoriel. Plutôt que de vérifier tous les axiomes définissant un espace vectoriel, on cherche si \(F\) n’est pas une partie d’un espace vectoriel \(E\) (souvent bien connu) puis on vérifie que c’est un sous-espace vectoriel de \(E\).
Intersection de sous-espaces vectoriels
(Une intersection de sous-espaces vectoriels est encore un sous-espace vectoriel). Soient \(\left(E,+,.\right)\) un \(\mathbb{K}\)-espace vectoriel et \(\left(F_i\right)_{i\in I}\) une famille de sous-espaces vectoriels de \(E\) alors \(\displaystyle{\bigcap_{i\in I} F_i}\) est un sous-espace vectoriel de \(E\).
Soit \(i \in I\), puisque \(F_i\) est un sous-espace vectoriel de \(E\), \(0_E
\in F_i\) et donc \(0_E \in \bigcap_{i \in I} F_i\). Soient \((x,y) \in \displaystyle{\bigcap_{i\in I}
F_i}^2\) et \((\alpha,
\beta) \in \mathbb{K} [2]\). Montrons que \(\alpha . x + \beta . y \in \displaystyle{\bigcap_{i
\in
I} F_i}\). Soit \(i \in I\), comme \(F_i\) est un sous-espace vectoriel de \(E\) et que \(x, y
\in F_i\), \(\alpha.x + \beta.y \in F_i\) ce qui montre que \(\alpha.x + \beta. y \in
\displaystyle{\bigcap_{i\in I} F_i}\).
L’intersection de deux droites vectorielles de l’espace \(\mathbb{R}^3\) dirigées par des vecteurs non colinéaires est égale au singleton \(0_{\mathbb{R} [3]} = \left\{\left(0,0,0\right)\right\}\) qui est bien un sous-espace vectoriel de \(\mathbb{R}^3\).
L’intersection de deux plans vectoriels dans l’espace est une droite vectorielle si ces deux plans ne sont pas confondus.
Dans \(\mathscr S\left(R\right)\), en notant \[F=\left\{\left(u_n\right) \in
\mathscr S\left(\mathbb{R}\right) ~|~ \left(u_n\right) \textrm{ est convergente }\right\} \textrm{ et } G=
\left\{\left(u_n\right) \in \mathscr S\left(\mathbb{R}\right) ~|~ \left(u_n\right) \textrm{ géométrique
de raison $r$ }\right\}\] où \(r\in\mathbb{R}\). Alors \[F\cap
G=\begin{cases} F \textrm{ si } r\in\left]-1,1\right]\newline \left\{\left(0\right)\right\}
\textrm{ sinon } \end{cases}\] qui sont dans les deux cas des sous-espaces vectoriels de \(\mathscr S\left(\mathbb{R}\right)\).
(Sous-espace vectoriel engendré par une partie d’un espace vectoriel). Soit \(A\) une partie d’un \(\mathbb{K}\)-espace vectoriel \(\left(E,+,.\right)\). On appelle sous-espace vectoriel engendré par \(A\) le plus petit sous-espace vectoriel de \(E\) contenant \(A\). On le note \(Vect\left(A\right)\) et on a : \[\displaystyle{Vect\left(A\right) = \bigcap_{F\in \mathscr F_A} F}\] où \(\mathscr F_A\) désigne l’ensemble des sous-espaces vectoriels de \(E\) qui contiennent \(A\).
D’après la proposition [prop_inter_sev], \(\bigcap_{F\in \mathscr F_A} F\) est un sous-espace vectoriel de \(E\). Il contient de plus \(A\) et par construction, il est inclus dans tout sous-espace vectoriel de \(E\) contenant \(A\). On a donc \(Vect\left(A\right) = \bigcap_{F\in \mathscr F_A} F\).
\(A\) est un sous-espace vectoriel de \(E\) si et seulement si \(Vect\left(A\right)=A\).
\(Vect\left(\varnothing\right)= \{0\}\).
(Sous-espace vectoriel engendré par une partie finie). Soient \(n\in \mathbb{N}^*\) et \(A=\left\{x_1,\dots,x_n\right\}\) une partie finie à \(n\) éléments de \(E\). Le sous-espace vectoriel engendré par \(A\) est l’ensemble des combinaisons linéaires finies d’éléments de \(A\) : \[\boxed{Vect{\left(A\right)} =\left\{ \lambda_1\cdot x_1 + \dots+ \lambda_n\cdot
x_n ~|~ \left(\lambda_1,\dots,\lambda_n\right)\in K^n\right\}}\]
Soit \(\mathscr A\) l’ensemble de toutes les combinaisons linéaires finies d’éléments de \(A\). L’ensemble \(\mathscr A\) est non vide et stable par combinaison linéaire. C’est donc un sous-espace vectoriel de \(E\). Montrons que \(\mathscr A\) est le plus petit sous-espace vectoriel de \(E\) contenant \(A\). Pour ce faire, il suffit de montrer que si \(\mathscr B\) est un sous-espace vectoriel de \(E\) contenant \(A\) alors \(\mathscr A\subset \mathscr B\). Soit \(x\in \mathscr A\). Par définition de \(\mathscr A\), il existe \(\alpha_1,\dots,\alpha_n\in\mathbb{K}\) et \(x_1,\dots,x_n\in A\) tels que \(x=\alpha_1 x_1+ \dots\alpha_n.x_n\). Comme \(A\subset \mathscr B\), il vient que \(x_1,\dots,x_n\in \mathscr B\) et comme \(\mathscr
B\) est un sous-espace vectoriel de \(E\), il est stable par combinaison linéaire et donc \(x=\alpha_1 x_1+ \dots\alpha_n.x_n\in B\). Ce qui prouve que \(\mathscr
A\subset \mathscr B\) et termine la démonstration.
Si \(u\in E\setminus\left\{0\right\}\), la droite vectorielle engendrée par \(u\) est le sous-espace vectoriel engendré par \(u\): \(Vect{\left(u\right)}=\left\{\lambda\cdot u
~|~ \lambda \in \mathbb{K}\right\}\).
Si \(u,v\in E\setminus\left\{0\right\}\), le plan vectoriel engendré par \(u\) et \(v\) est le sous-espace vectoriel engendré par \(\left\{u,v\right\}\): \(Vect{\left(\left\{u,v\right\}\right)}=\left\{\alpha\cdot u + \beta \cdot v ~|~ \left(\alpha,\beta\right)
\in \mathbb{K}^2\right\}\).
(Pour montrer que \(F\) est un sous-espace vectoriel de \(E\)). Il suffit de décrire \(F\) sous forme d’un \(Vect\).
Les sous-ensembles de \(\mathbb{C}\) donnés par \(G=\mathbb{R}\) et \(F=i\mathbb{R}\) s’écrivent \(G=Vect\left(1\right)\) et \(G=Vect\left(i\right)\) donc ce sont des sous-espaces vectoriels de \(\mathbb{C}\).
Si \(u\) est un vecteur du plan (ou de l’espace) alors \(F=\left\{\lambda u ~|~ \lambda \in\mathbb{R}\right\}=Vect\left(u\right)\) donc \(F\) est un sous-espace vectoriel du plan (ou de l’espace).
Si \(u\) et \(v\) sont des vecteurs du plan (ou de l’espace) alors \(F=\left\{\alpha u+\beta v ~|~ \alpha,\beta \in\mathbb{R}\right\}=Vect\left(u,v\right)\) donc \(F\) est un sous-espace vectoriel du plan (ou de l’espace).
On a \(F=\left\{\left(x,y,z\right)\in\mathbb{R}^3 ~|~ 2x+y-z=0\right\}=\left\{\left(x,y,2x+y\right)~|~
x,y\in\mathbb{R}\right\}=\left\{x\left(1,0,2\right)+y\left(0,1,1\right)~|~ x,y\in\mathbb{R}\right\}=Vect\left(\left(1,0,2\right),\left(0,1,1\right)\right)\) donc \(F\) est un sous-espace vectoriel de \(\mathbb{R}^3\). C’est le plan vectoriel engendré par les vecteurs \(\left(1,0,2\right),\left(0,1,1\right)\).
Soit \(F\) l’ensemble des solutions de l’équation différentielle \(y''+\omega y=0\) avec \(\omega\in\mathbb{R}^+\). Alors après avoir résolu l’équation, on trouve que \(F=Vect\left(x\mapsto \cos \omega x,x\mapsto \sin\omega x\right)\). Ainsi \(F\) est donc un sous-espace vectoriel de \(\mathcal{C}^{0}\left(\mathbb{R}\right)\).
On a \(F=\left\{P\in\mathbb{R}_3\left[X\right]~|~ P\left(1\right)=0\right\}=\left\{\left(X-1\right)\left(aX^2+bX+c\right)~|~
a,b,c\in\mathbb{R}\right\}=\left\{aX^2\left(X-1\right)+bX\left(X-1\right)+c\left(X-1\right)~|~
a,b,c\in\mathbb{R}\right\}=Vect\left(X^2\left(X-1\right),X\left(X-1\right),\left(X-1\right)\right)\) donc \(F\) est un sous-espace vectoriel de \(\mathbb{R}_3\left[X\right]\).
La remarque suivante permet de fixer les choses dans l’espace :
Dans l’espace \(\mathbb{R}^3\), soit \(\mathscr F=\left\{ u, v, w\right\}\) où \(u\), \(v\) et \(w\in \mathbb{R}^3\). Alors : \[Vect\left(\mathscr F\right)= \begin{cases} \bullet \textrm{ La droite dirigée par $
u$ si les trois vecteurs sont colinéaires}\\\bullet \textrm{ Le plan engendré par
$ u$ et $ v$ si les trois vecteurs sont coplanaires mais tels}\\\textrm{ que
deux d'entre eux, $ u$ et $ v$ par exemple, ne sont pas colinéaires} \newline
\bullet \textrm{ L'espace $\mathbb{R}^3$ si les trois vecteurs ne sont pas
coplanaires
}\end{cases}\] Donc les sous-espaces vectoriels de \(\mathbb{R}^3\) sont :
L’ensemble réduit au vecteur nul \(\left\{0\right\}\)
Les droites passant pas \(0\).
Les plans passant par \(0\).
L’espace tout entier.
Giuseppe Peano, né le 27 août 1858 à Spinetta di Cuneo et mort le 20 avril 1932 à Turin.
Les-mathematiques.net
Giuseppe Peano a été un des premiers mathématiciens à comprendre la nécessité de l’axiomatisation des mathématiques. Celles-ci doivent reposer sur quelques règles simples desquelles on fait découler les théorèmes après avoir défini avec précision les objets utilisés. Grâce à cette démarche et à sa grande rigueur, il mit en évidence de nombreuses erreurs dans les traités mathématiques alors existants. Il comprit aussi l’importance de la théorie des ensembles et de la logique pour exprimer les mathématiques et généralisa au reste des mathématiques l’usage des symboles issus de ces théories . Il fut le premier à utiliser les symboles d’union et d’intersection.
Giuseppe Peano s’intéressa au début de sa carrière au calcul infinitésimal qu’il participe à formaliser et à rendre plus rigoureux. À partir de 1887, son travail se porte sur la construction formelle des mathématiques et il définit de manière axiomatique l’ensemble des entiers naturels. Ce système d’axiomes porte maintenant son nom. Grâce aux travaux de Grassmann, il axiomatise la notion d’espace vectoriel.
À partir de 1900, il s’attelle à deux grands chantiers. Le premier consiste en la construction d’un langage international qu’il baptisa Interlingua basé sur un latin simplifié et augmenté de vocabulaire anglais, allemand et français. Le second est l’écriture d’une encyclopédie mathématique Formulario Mathematico utilisant le formalisme qu’il a inventé et qui vise à contenir toutes les mathématiques alors connues. Notons que Peano, excellent enseignant au début de sa carrière finit sa vie piètre pédagogue, ses cours étant rendu complètement obscurs par ses notations.
Si \(F\) et \(G\) sont deux sous-espaces vectoriels de \(E\), ce n’est pas forcément le cas de \(F\cup G\) et jamais le cas de \(F\setminus G\), \(G\setminus F\) et \(E\setminus F\) car ils ne contiennent pas le vecteur nul. Par exemple :
Deux droites vectorielles \(\mathcal D_1\) et \(\mathcal D_2\) du plan \(\mathbb{R}^2\) sont des sous-espaces vectoriels de \(\mathbb{R}^2\) mais ce n’est pas le cas de leur réunion à moins que ces deux droites ne soient confondues. En effet, si ces deux droites ne sont pas confondues, la somme d’un vecteur non nul \(u_1\) de la première droite et d’un vecteur non nul \(u_2\) de la seconde n’est un vecteur d’aucune des deux droites et n’appartient donc pas à leur réunion.
La partie \(F=\left\{P\in\mathbb{R}\left[X\right]~|~ P(0)=0\right\}\) de \(E=\mathbb{R}\left[X\right]\) est un sous-espace vectoriel de \(E\) mais ce n’est pas le cas de \(E\setminus
F\). En effet, les polynômes de \(E\setminus
F\) sont ceux qui ne s’annulent pas en \(0\) donc \(E\setminus
F\) ne contient pas le polynôme nul.
Somme de sous-espaces vectoriels
Définitions
(Somme de deux sous-espaces vectoriels). Soient \(F\) et \(G\) deux sous-espaces vectoriels d’un \(\mathbb{K}\)-espace vectoriel \(\left(E,+,\cdot\right)\). On appelle somme de \(F\) et \(G\) et on note \(F+G\) le sous-espace vectoriel de \(E\) donné par \[F+G=\left\{x+y~|~ \left(x,y\right)\in F\times G\right\}\]
Le sous-ensemble \(F+G\) est bien un sous-espace vectoriel de \(E\). En effet, \(F+G\subset E\) car \(E\) est stable pour l’addition. De plus, \(F+G\) est non vide car \(F\) et \(G\) le sont. Enfin, si \(u=x+y\in F+G\) et \(u'=x'+y'\in F+G\) avec \(x,x'\in F\) et \(y,y'\in G\) alors, pour \(\alpha,\beta\in\mathbb{K}\), \[\alpha u+\beta u'=\underbrace{\alpha x+\beta x'}_{\in F}+ \underbrace{\alpha y+\beta y'}_{\in G} \in F+G\] car \(F\) et \(G\) sont des sous-espaces vectoriels.
(La somme de deux sous-espaces vectoriels est le plus petit sous-espace vectoriel contenant leur réunion). Soient \(F\) et \(G\) deux sous-espaces vectoriels d’un \(\mathbb{K}\)-espace vectoriel \(\left(E,+,\cdot\right)\). Alors \(F+G\) est le plus petit sous-espace vectoriel de \(E\) contenant \(F\cup G\).
On a prouvé dans la remarque précédente que \(F+G\) est un sous-espace vectoriel de \(E\). Il contient \(F\) et \(G\) car \(0_E\) est élément de \(F\) et \(G\) et donc \(F=F+0_E\subset F+G\) et \(G=0_E+G\subset F+G\). De plus, si on considère un sous-espace \(H\) de \(E\) qui contient \(F\cup G\) alors montrons que \(F+G\subset
H\). Soient \(x+y\in F+G\) avec \(x\in F\) et \(y\in G\). Comme \(F\cup G\subset H\), on a aussi \(x,y\in H\) et comme \(H\) est un sous-espace vectoriel, il s’ensuit que \(x+y\in H\). Donc \(F+G\subset H\) et \(F+G\) est le plus petit sous-espace vectoriel de \(E\) contenant \(F\) et \(G\).
Soient deux droites vectorielles \(\mathscr D_1\) et \(\mathscr D_2\) du plan euclidien \(\mathscr P\). On a : \(\mathscr D_1+\mathscr D_2=\mathscr P\) si \(\mathscr D_1\) et \(\mathscr D_2\) sont dirigées par des vecteurs non colinéaires et \(\mathscr D_1+\mathscr D_2=\mathscr D_1=\mathscr D_2\) sinon.
Soient \(\mathscr D\) une droite vectorielle de l’espace \(\mathscr V\) dirigée par un vecteur \(u\) et \(\mathscr P\) un plan vectoriel de l’espace. On a : \(\mathscr D + \mathscr P=\mathscr V\) si \(u \not\in\mathscr P\) et \(\mathscr D + \mathscr P=\mathscr P\) sinon (la droite est alors incluse dans le plan \(\mathscr P\)).
Dans \(\mathscr F\left(\mathbb{R},\mathbb{R}\right)\) soient \(F=Vect\left(\sin\right)\) et \(G=Vect\left(exp\right)\) alors : \[F+G=Vect\left(\sin,\exp\right)=\left\{x\mapsto \alpha \sin \left(x\right) + \beta \exp\left(x\right)
~|~ \alpha,\beta\in\mathbb{R}\right\}\]
La proposition suivante est bien pratique pour calculer des sommes :
(Calcul pratique d’une somme de \(Vect\)). Soient \(A\) et \(B\) deux parties d’un \(K\)-espace vectoriel \(E\) alors \[\boxed{Vect\left(A\right)+Vect\left(B\right)=Vect\left(A\cup B\right)}\]
Dans l’espace \(\mathbb{R}^{3}\), on considère les parties \(F=\{ (x,0,0) ~|~ x\in \mathbb{R} \}\) et \(G=\{ (x,x,0) ~|~ x\in \mathbb{R} \}\). Montrons que ce sont des sous-espaces vectoriels de \(\mathbb{R}^3\) et déterminons le sous-espace \(F+G\). On a \(F=Vect\left(1,0,0\right)\) et \(G=Vect\left(1,1,0\right)\) donc \(F\) et \(G\) sont des sous-espaces vectoriels de \(\mathbb{R}^3\). De plus \(F+G=Vect\left(\left(1,0,0\right),\left(1,1,0\right)\right)\) et on reconnait que \(F+G\) est le plan vectoriel de \(\mathbb{R}^3\) engendré par \(\left(1,0,0\right)\) et \(\left(1,1,0\right)\).
Somme directe
(Somme directe). On dit que deux sous-espaces vectoriels \(F\) et \(G\) de \(E\) sont en somme directe si \(F\cap G=\left\{0\right\}\). On note alors \(F\oplus G\) leur somme.
(Caractérisation de la somme directe). Soient \(F\) et \(G\) deux sous-espaces vectoriels du \(\mathbb{K}\)-espace vectoriel \(\left(E,+,\cdot\right)\). On a équivalence entre :
\(F\) et \(G\) sont en somme directe.
\(\forall x\in F+G,\quad \exists~ ! \left(x_1,x_2\right)\in F\times G:\quad
x=x_1+x_2\) (c’est-à-dire, vecteur de \(F+G\) se décompose de manière comme somme d’un vecteur de \(F\) et d’un vecteur de \(G\).)
Supposons que \(F\) et \(G\) soient en somme directe et soit \(x\in F+G\). Par définition, il existe \(x_1\in F\) et \(x_2\in G\) tels que \(x=x_1+x_2\). Supposons qu’il existe \(x_1'\in F\) et \(x_2'\in G\) tels qu’on ait encore \(x=x_1'+x_2'\). Comme \(x=x_1+x_2=x_1'+x_2'\), on a l’égalité : \(x_1-x_1'=x'_2-x_2\). Notons \(y\) ce vecteur. Comme \(F_1\) et \(F_2\) sont des sous-espaces vectoriels de \(E\), \(y=x_1-x_1'\in F_1\) et \(y=x_2'-x_2\in F_2\). Par conséquent \(y\in F_1\cap F_2\). Mais \(F_1\) et \(F_2\) étant en somme directe, on a \(F_1\cap F_2=\left\{0\right\}\) donc \(y=0\). Par conséquent, \(x_1=x_1'\) et \(x_2=x_2'\) et l’unicité est prouvée.
Prouvons maintenant la réciproque. Soit \(x\in F\cap
G\). Il existe alors deux couples de \(F\times G\) permettant de décomposer \(x\) en un vecteur de \(F\) et un vecteur de \(G\) : \(\left(x,0\right)\) et \(\left(0,x\right)\). Par hypothèse, elles sont égales : \(\left(x,0\right)=\left(0,x\right)\). Par conséquent \(x=0\) et les sous-espaces \(F\) et \(G\) sont en somme directe.
(Pour montrer que \(F\) et \(G\) sont en somme directe).
Soit \(x\in F\cap G\).
\(x\in F\) donc ...
\(x\in G\) donc ...
... alors \(x=0\).
Dans \(\mathbb{C}\), les sous-espace vectoriels \(F=\mathbb{R}\) et \(G=i\mathbb{R}\) sont en somme directe :
Soit \(x\in F\cap G\).
\(x\in F\) donc \(x\) est réel.
\(x\in G\) est imaginaire pur.
Le seul complexe à la fois réel et imaginaire pur est \(0\) donc \(x=0\).
Dans \(\mathbb{R}^3\), les droites vectorielles \(F=\begin{cases}
x+y-z&=0\\2x-y+z&=0 \end{cases}\) et \(G=\begin{cases} x+y-2z&=0\\-y+z&=0
\end{cases}\) sont en somme directe.
Montrons que \(F\) est bien un sous-espace vectoriel de \(\mathbb{R}^3\). On a : \[\begin{cases}
x+y-z&=0\\2x-y+z&=0 \end{cases} \Longleftrightarrow\begin{cases}
x+y-z&=0\newline-y+z&=0 \end{cases} \Longleftrightarrow x=0 \quad \textrm{ et} \quad y=z\] donc \[F=\left\{\left(x,y,z\right)\in\mathbb{R}^3~|~ x+y-z=0 \quad \textrm{ et} \quad 2x-y+z=0\right\}=\left\{\left(0,y,y\right)~|~
y\in\mathbb{R}\right\}=Vect\left(0,1,1\right) .\]
On montre de la même façon que \(G=Vect\left(1,1,1\right)\) et donc \(G\) est bien un sous-espace vectoriel de \(\mathbb{R}^3\).
Ces deux droites vectorielles ne sont pas engendrées par des vecteurs colinéaires. Elles ne se coupent donc qu’en \(0_{\mathbb{R}^3}\).
Dans \(E=\mathcal F\left(\mathbb{R},\mathbb{R}\right)\), on considère \(F=\left\{f\in E~|~ f\left(0\right)=0\right\}\) et \(G=Vect\left(x\mapsto 1\right)\). On a montré dans l’item 5. de l’exemple [ex03/03/201013:45] page [ex03/03/201013:45] que \(F\) est un sous-espace vectoriel de \(E\). Comme \(G\) est décrit par un \(Vect\), c’est un sous-espace vectoriel de \(E\). Remarquons que \(G\) est l’ensemble des applications constantes de \(\mathbb{R}\) dans \(\mathbb{R}\).
Soit \(f\in F\cap G\).
\(f\in F\) donc \(f\left(0\right)=0\).
\(f\in G\) donc il existe \(a\in\mathbb{R}\) tel que \(f:x\mapsto a\).
Mais \(a=f\left(0\right)=0\) donc \(f=0\).
Toujours dans \(E=\mathscr
F\left(\mathbb{R},\mathbb{R}\right)\), les sous-espaces vectoriels \(F=Vect\left(\cos\right)\) et \(G=Vect\left(\sin\right)\) sont en somme directe. Il est clair que \(F\) et \(G\) sont des sous-espaces vectoriels de \(E\). Montrons qu’ils sont en somme directe
Soit \(f\in F\cap G\).
\(f\in F\) donc il existe \(\alpha \in\mathbb{R}\) tel que \(f=\alpha \cos\).
\(f\in G\) donc il existe \(\beta \in\mathbb{R}\) tel que \(f=\beta \sin\).
et il vient que \(\forall x\in\mathbb{R},\quad \alpha \cos x=\beta \sin x\) ce qui n’est possible que si \(\alpha=\beta=0\). En effet, comme précisé, l’égalité précédente est vraie pour tout réel \(x\). En particulier, si \(x=0\), alors \(\alpha=0\) et si \(x=\pi/2\), on trouve que \(\beta=0\). Finalement, \(f=0\).
Sous-espaces supplémentaires
(Sous-espaces supplémentaires). On dit que deux sous-espaces vectoriels \(F\) et \(G\) de \(E\) sont supplémentaires si et seulement si ils vérifient :
\(E=F+G\)
\(F\cap G=\left\{0\right\}\)
Les-mathematiques.net
Décomposition d’un vecteur suivant deux sous-espaces supplémentaires
L’intérêt de disposer d’espaces supplémentaires est donné par le théorème suivant. Il dit que si on dispose de deux sous-espaces supplémentaires \(F\) et \(G\) dans un \(\mathbb{K}\)-espace vectoriel \(E\) alors tout vecteur de \(E\) peut être décomposé de manière unique en la somme d’un vecteur de \(F\) et d’un vecteur de \(G\).
(Caractérisation des sous-espaces supplémentaires). Soient \(F\) et \(G\) deux sous-espaces vectoriels d’un \(\mathbb{K}\)-espace vectoriel \(\left(E,+,\cdot\right)\). On a équivalence entre :
\(E=F\oplus G\) (c’est-à-dire \(F\) et \(G\) sont supplémentaires).
\(\forall x\in E,\quad \exists~ ! \left(x_1,x_2\right)\in F\times G:\quad x=x_1+x_2\) (c’est-à-dire, vecteur de \(E\) se décompose de manière comme somme d’un vecteur de \(F\) et d’un vecteur de \(G\).)
Supposons que \(F\) et \(G\) sont supplémentaires. Soit \(x\in E\). Comme \(E=F+G\), il existe \(x_1 \in F\) et \(x_2 \in G\) tels que \(x=x_1 + x_2\). En appliquant le théorème [caracterisation_somme_direct], comme \(F\) et \(G\) sont en somme directe, cette décomposition est unique.
Réciproquement, si pour tout \(x \in E\), il existe un unique couple \(\left(x_1,x_2\right)\in F\times G\) tel que \(x=x_1+x_2\) alors on a nécessairement \(E=F+G\). On peut de plus appliquer à nouveau le théorème [caracterisation_somme_direct] et affirmer que les deux sous-espaces \(F\) et \(G\) sont supplémentaires. On a ainsi montré que \(E=F\oplus G\).
La partie souvent difficile dans ce plan est souvent de montrer que \(E=F+G\). Dans ce chapitre, on utilisera une des deux techniques suivantes :
Si on sait écrire \(F\) et \(G\) sous forme d’un \(Vect\), \(F=Vect\left(A\right)\), \(G=Vect\left(B\right)\), on peut, grâce à la proposition [prop_calcul_pratique_vect], écrire \(F+G=Vect\left(A\right)+Vect\left(B\right)=Vect\left(A\cup B\right)\). Reste alors à montrer que \(Vect\left(A\cup B\right)=E\).
Si cette technique ne fonctionne pas, on utilise alors la définition : Soit \(x\in E\). Posons \(x_1= \dots\). Posons \(x_2=\dots\). On a bien :
\(x_1\in F\).
\(x_2\in G\).
\(x=x_1+x_2\).
La difficulté de cette méthode consiste en la détermination de \(x_1\) et \(x_2\). On procède souvent ainsi. Dans la pratique, il est souvent facile de déterminer un des deux vecteurs \(x_1\) ou \(x_2\), supposons que ce soit \(x_1\). On pose alors \(x_2=x-x_1\). Il suffit alors de vérifier que \(x_2\in G\).
On verra au chapitre [chap_dim_ev] que grâce à la formule de Grassmann (voir [dim_somme_sev] page [dim_somme_sev]) on arrivera à traiter très simplement cette question dans le cas où on travaille avec des espaces vectoriels de dimension finie.
Dans \(E=\mathbb{C}\), \(F=Vect\left(\left\{1\right\}\right)\) et \(G=Vect\left(\left\{i\right\}\right)\). On sait que \(F\) et \(G\) sont des sous-espaces vectoriels de \(E\).
Si \(x\in F\cap G\) alors \(x\) est à la fois réel et imaginaire pur donc \(x=0\) et \(F\cap G=\left\{0\right\}\).
\(F+G=Vect\left(1\right)+Vect\left(i\right)=Vect\left(1,i\right)=\mathbb{C}\) donc \(E=F+G\).
On a montré que \(E=F\oplus G\).
Dans l’espace \(E=\mathbb{R}^3\) la droite \(F\) donnée par le système \(\begin{cases}
x+y-z&=0\newline2x-y+z&=0 \end{cases}\) et le plan \(G\) d’équation \(z=0\) sont supplémentaires. Comme \(F=Vect\left(0,1,1\right)\) et \(G=Vect\left(\left(1,0,0\right),\left(0,1,0\right)\right)\), \(F\) et \(G\) sont bien des sous-espaces vectoriels de \(E\).
Si \(\left(x,y,z\right)\in F\cap G\) alors \(\left(x,y,z\right)\) vérifie le système \(\begin{cases}
x+y-z&=0\\2x-y+z&=0\newlinez&=0 \end{cases}\) et on trouve que \(x=y=z=0\) donc \(F\cap
G=\left\{0\right\}\).
\(F+G=Vect\left(-4,1,-3\right)+Vect\left(\left(1,0,0\right),\left(0,1,0\right)\right)=Vect\left(\left(-4,1,-3\right),\left(1,0,0\right)
, \left(0,1,0\right)\right)=E\) car on vérifie, en utilisant par exemple le produit mixte, que ces trois vecteurs ne sont pas coplanaires. Ils forment ainsi une base de \(\mathbb{R}^3\).
On a montré que \(E=F\oplus G\).
Dans \(E=\mathcal F\left(\mathbb{R},\mathbb{R}\right)\), on pose \(F= \left\{\textrm{ fonctions paires}\right\}\) et \(G=
\left\{\textrm{ fonctions impaires}\right\}\). On vérifie que \(F\) est un sous-espace vectoriel de \(E\). \(F\) est non vide, il contient par exemple la fonction identiquement nulle sur \(\mathbb{R}\). Si \(\alpha,\beta\in\mathbb{R}\) et si \(f,g\in F\) alors, en utilisant la parité de \(f\) et \(g\), pour tout \(x\in\mathbb{R}\) : \[\left(\alpha f+\beta g\right)\left(-x\right)=\alpha f\left(-x\right)+\beta g\left(-x\right)=\alpha f\left(x\right)+\beta
g\left(x\right) =\left(\alpha f+\beta g\right)\left(x\right)\] donc \(\alpha f+\beta g \in F\). On prouve de même que \(G\) est un sous-espace vectoriel de \(E\).
Soit \(f\in F\cap G\) alors \(\forall x\in\mathbb{R},f\left(-x\right)=f\left(x\right)=-f\left(x\right)\) et donc \(f=0\). Alors \(F\cap G=\left\{0\right\}\).
Soit \(f\in E\). On cherche deux fonctions \(f_1\) et \(f_2\) telles que \(f_1\) est paire, \(f_2\) impaire et \(f=f_1+f_2\). Effectuons un raisonnement par analyse et synthèse.
Supposons que deux telles fonctions existent. Pour tout \(x\in\mathbb{R}\), on sait que \(f(x)=f_1(x)+f_2(x)\) et que \(f(-x)=f_1(x)-f_2(x)\). On tire de ces deux égalités que \[f_1\left(x\right)=\dfrac{f\left(x\right)+f\left(-x\right)}{2} \quad \textrm{ et} \quad f_2\left(x\right)=\dfrac{f\left(x\right)-f\left(-x\right)}{2}.\]
Posons \(f_1\left(x\right)=\dfrac{f\left(x\right)+f\left(-x\right)}{2} \quad \textrm{ et} \quad
f_2\left(x\right)=\dfrac{f\left(x\right)-f\left(-x\right)}{2}.\) On vérifie facilement que \(f_1\) est paire, donc que \(f_1\in F\) et que \(f_2\) est impaire, donc que \(f_2\in G\). On vérifie aussi que \(f=f_1+f_2\).
Finalement, on a montré que \(E=F+G\).
On a donc \(\mathcal F\left(\mathbb{R},\mathbb{R}\right)=F\oplus G\). Que dire des fonctions \(\exp\), \(\mathop{\mathrm{ch}}\) et \(\mathop{\mathrm{sh}}\)?
Toujours dans \(E=\mathcal F\left(\mathbb{R},\mathbb{R}\right)\), on pose \(F= \left\{f\in E~|~
f\left(1\right)=0\right\}\) et \(G=\left\{x\mapsto ax~|~ a\in\mathbb{R}\right\}\). On vérifie facilement que \(F\) et \(G\) sont des sous-espaces vectoriels de \(E\). Pour \(G\), on peut remarque que \(G=Vect\left(\mathop{\mathrm{id}}\nolimits_\mathbb{R}\right)\).
Soit \(f\in F\cap G\). Comme \(f\in F\), \(f\left(1\right)=0\) et comme \(f\in G\) alors il existe \(a\in\mathbb{R}\) tel que \(f:x\mapsto ax\). Alors \(f\left(1\right)=a=0\) et donc \(f=0\). On a montré que \(F\cap G=\left\{0\right\}\).
Soit \(f\in E\). S’il existe \(f_1\in F\) et \(f_2\in G\) tels que \(f=f_1+f_2\) alors \(f\left(1\right)=f_2\left(1\right)\). On est alors invité à poser \(f_2:x\mapsto f\left(1\right)x\). Il est clair que \(f_2\in G\). Posons \(f_1=f-f_2\). Il est clair que \(f_1\left(1\right)=0\) donc \(f_1\in F\). On a bien de plus \(f=f_1+f_2\). Donc \(E=F+G\).
En conclusion \(E=F\oplus G\).
Applications linéaires
Dans toute la suite \(\left(E,+,\cdot\right)\) et \(\left(F,+,\cdot\right)\) sont deux \(\mathbb{K}\)-espaces vectoriels.
Définitions
(Application linéaire). Soient \(\left(E,+,\cdot\right)\) et \(\left(F,+,\cdot\right)\) deux \(\mathbb{K}\)-espaces vectoriels et \(f:E
\rightarrow F\). On dit que \(f\) est linéaire si et seulement si :
(On dit aussi que \(f\) est un morphisme d’espaces vectoriels).
(Caractérisation des applications linéaires).
Soit \(f:E \rightarrow F\). \(f\) est linéaire si et seulement si : \[\forall \left(x,y\right)\in E^2, \quad \forall \left(\alpha,\beta\right)\in\mathbb{K}^2, \quad
\boxed{ f\left(\alpha \cdot x + \beta \cdot y\right)=\alpha \cdot f\left(x\right)+\beta\cdot
f\left(y\right)}\]
Si \(f:E \rightarrow F\) est linéaire alors \(f\left(0_E\right)=0_F\). En effet \(f(0_E)=f(0_E+0_E)=f(0_E)+f(0_E)\) donc par soustraction du vecteurs \(f(0_E)\) des deux côtés de cette égalité, il vient \(f(0_E)=0_F\).
(Pour montrer que \(f:E \rightarrow F\) est linéaire).
Soient \(\alpha,\beta\in\mathbb{R}\) et \(x,y\in E\).
Montrons que \(f\left(\alpha \cdot x + \beta \cdot y\right)=\alpha \cdot
f\left(x\right)+\beta\cdot f\left(y\right)\)
(Pour montrer que \(f:E \rightarrow F\) n’est pas linéaire). on peut :
montrer que \(f\left(0_E\right)\neq 0_F\).
ou trouver \(\alpha,\beta\in \mathbb{K}\), \(x,y\in E\) tels que \(f\left(\alpha \cdot x
+ \beta \cdot y\right)\neq \alpha \cdot
f\left(x\right)+\beta\cdot f\left(y\right)\)
(Forme linéaire, endomorphisme, isomorphisme, automorphisme). Soit \(f:E\rightarrow F\) une application linéaire.
Si \(F=\mathbb{K}\), on dit que \(f\) est une forme linéaire. On note \(E^*\) l’ensemble des formes linéaires sur \(E\).
Si \(E=F\), on dit que \(f\) est un endomorphisme de \(E\).
Si \(f:E\rightarrow F\) est bijective, on dit que \(f\) est un isomorphisme de \(E\) sur \(F\).
Si \(f\) est à la fois un endomorphisme de \(E\) et un isomorphisme, on dit que \(f\) est un automorphisme de \(E\).
Les applications linéaires \(f:\mathbb{R}\rightarrow \mathbb{R}\) sont les applications \(x\mapsto \lambda \cdot x\) où \(\lambda \in \mathbb{R}\). Montrons qu’une telle application est linéaire. Soient \(\alpha,\beta\in\mathbb{R}\) et \(x,y\in \mathbb{R}\) alors \(f\left(\alpha x+\beta y\right)=\lambda\left(\alpha x+\beta y\right)=\alpha \lambda x + \beta
\lambda y=\alpha f\left(x\right)+\beta f\left(y\right)\). Donc \(f\) est linéaire. Montrons que les applications \(f\) de cette forme sont les seules qui soient linéaires sur \(\mathbb{R}\). Si \(f\) est linéaire sur \(\mathbb{R}\) alors on doit avoir, pour tout \(x\in\mathbb{R}\), \(f\left(x\right)=f\left(x.1\right)=xf\left(1\right)\) donc \(f\) est de la forme indiquée avec \(\lambda=f\left(1\right)\).
Dans un \(\mathbb{K}\)-espace vectoriel quelconque \(E\), les homothéties \(h: \left\{ \begin{array}{ccl} E & \longrightarrow & E \\ x & \longmapsto & \lambda \cdot x \end{array} \right.\) où \(\lambda \in
\mathbb{K}\) sont linéaires. La preuve est identique à celle donnée dans l’item précédent.
Les translations de vecteur non nul ne sont pas linéaires...En effet, dans un \(\mathbb{K}\)-espace vectoriel \(E\), pour \(u\in E\) tel que \(u\neq 0\), considérons la translation \(t_u: \left\{ \begin{array}{ccl} E & \longrightarrow & E \\ x & \longmapsto & x+u \end{array} \right.\). On a \(t_u\left(0_E\right)=0_E+u=u\neq 0_F\) donc \(t_u\) n’est pas linéaire.
La dérivation \(D: \left\{ \begin{array}{ccl} \mathcal{C}^{1}\left(\mathbb{R}\right) & \longrightarrow & \mathcal{C}^{0}\left(\mathbb{R}\right) \\ f & \longmapsto & D\left(f\right)=f' \end{array} \right.\) est linéaire. Si \(\alpha,\beta\in \mathbb{R}\) et \(f,g\in \mathcal{C}^{1}\left(\mathbb{R}\right)\) alors \(D\left(\alpha f +
\beta g\right)=\left(\alpha f +
\beta g\right)'=\alpha f' +
\beta g'=\alpha D\left(f\right)+\beta D\left(g\right)\).
L’application \(\varphi: \left\{ \begin{array}{ccl} \mathcal{C}^{0}([0,1],\mathbb{R} ) & \longrightarrow & \mathbb{R} \\ f & \longmapsto & \int_0^1 f(x)\mathrm{ \;d}x \end{array} \right.\) est une forme linéaire. En effet, si \(\alpha,\beta\in \mathbb{R}\) et \(f,g\in
\mathcal{C}^{0}\left([0,1],\mathbb{R} \right)\) alors \(\varphi\left(\alpha f +
\beta g\right)=\int_{0}^{1} \left(\alpha f +
\beta
g\right)\left(x\right)\,\textrm{d}x=\alpha\int_{0}^{1} f\left(x\right)\,\textrm{d}x+\beta\int_{0}^{1} g\left(x\right)\,\textrm{d}x=\alpha
\varphi\left(f\right)+\beta \varphi\left(g\right)\).
L’application \(\varphi: \left\{ \begin{array}{ccl} \mathbb{R}^3 & \longrightarrow & \mathbb{R}^2 \\ \left(x,y,z\right) & \longmapsto & \left(x-y+z,2x+z\right) \end{array} \right.\) est linéaire. Si \(\alpha\), \(\beta\in\mathbb{R}\) et si \(\left(x,y,z\right),\left(x',y',z'\right)\in\mathbb{R}^3\) alors \[\begin{aligned}
\varphi\left(\alpha\left(x,y,z\right)+\beta\left(x',y',z'\right)\right)&=&\varphi\left(\alpha
x+\beta x',\alpha
y+\beta y',\alpha z+\beta z'\right)\\ &=&\left( \alpha x+\beta x'-\left(\alpha
y+\beta y'\right)+ \alpha z+\beta z' ,2\left(\alpha x+\beta
x'\right)+\alpha z+\beta
z'\right)\\&=&\alpha\left(x-y+z,2x+z\right)+\beta\left(x'-y'+z',2x'+z'\right)\newline&=&\alpha\varphi\left(x,y,z\right)
+\beta\varphi\left(x',y',z'\right).\end{aligned}\]
Noyau, image d’une application linéaire
Rappels : Soient \(f:E\rightarrow F\) et \(E'\subset E\), \(F'\subset F\). Par définition :
L’image de \(E'\) par \(f\) est \(f\left(E'\right)=\left\{f\left(x\right) ~|~ x\in E'\right\}\)
L’image réciproque de \(F'\) par \(f\) est \(f^{-1}\left(F'\right)=\left\{x\in E~|~
f\left(x\right)\in F'\right\}\)
(Image directe et réciproque d’une application linéaire). Soit \(f:E\rightarrow G\) une application linéaire. Soient \(E'\) un sous-espace vectoriel de \(E\) et \(F'\) un sous-espace vectoriel de \(F\) alors :
\(f\left(E'\right)\) est un sous-espace vectoriel de \(F\).
\(f^{-1}\left(F'\right)\) est un sous-espace vectoriel de \(E\).
Comme \(0_E\in E'\) et que \(f\) est linéaire, \(0_F=f\left(0_E\right)\in f\left(E'\right)\) et \(f\left(E'\right)\) est non vide. Soient \(\alpha, \alpha' \in \mathbb{K}\) et \(y,y'\in f\left(E'\right)\). Il existe \(x,x'\in E\) tels que \(y = f\left(x\right)\) et \(y'=f\left(x'\right)\). Montrons que \(\alpha y
+ \alpha' y' \in f\left(E'\right)\). En utilisant la linéarité de \(f\) : \(\alpha y + \alpha'
y' = \alpha f\left(x\right)+ \alpha' f\left(x'\right) = f\left(\alpha x + \alpha' x`\right)\) et donc \(\alpha y + \alpha' y' \in f\left(E'\right)\). \(f\left(E'\right)\) est donc bien un sous-espace vectoriel de \(F\).
De même que précédemment, comme \(0_F\in F'\) et que \(f\) est linéaire, \(0_E
\in f^{-1}\left(F'\right)\). Soient \(\alpha, \alpha' \in \mathbb{K}\) et \(x,x' \in f^{-1}\left(F'\right)\). Il existe donc \(y,y'\in F'\) tels que \(y = f\left(x\right)\) et \(y'=f\left(x'\right)\). Donc, toujours par linéarité de \(f\), \(f\left(\alpha x + \alpha' x'\right) =\alpha y + \alpha'
y' \in F'\). Il vient alors que \(\alpha x + \alpha' x' \in f^{-1}\left(F'\right)\).
(Noyau, Image). Soit \(f:E\rightarrow F\) une application linéaire. On appelle :
Noyau de \(f\) et on note \(\operatorname{Ker}f\) le sous-ensemble de \(E\) : \(\operatorname{Ker}
f=\left\{x\in E ~|~ f\left(x\right)=0_F\right\}\)
Image de \(f\) et on note \(\mathop{\mathrm{Im}}f\) le sous-ensemble de \(F\) : \(\mathop{\mathrm{Im}}
f=\left\{f\left(x\right) ~|~ x\in E\right\}\).
(\({\rm Ker}\,f\) et \(\mathop{\mathrm{Im}}f\) sont des sous-espaces vectoriels). Soit \(f:E\rightarrow F\) une application linéaire. Alors \({\operatorname{Ker}f}\) et \({\mathop{\mathrm{Im}}f}\) sont des sous-espaces vectoriels de \(E\).
C’est un corollaire immédiat du théorème
Dans \(\mathbb{R}^3\), \(F=\left\{\left(x,y,z\right) \in\mathbb{R}^3 ~|~ x+y-z=0\right\}\) est un sous-espace vectoriel de \(\mathbb{R}^3\). En effet, posons \(f: \left\{ \begin{array}{ccl} \mathbb{R}^3 & \longrightarrow & \mathbb{R} \\ \left(x,y,z\right) & \longmapsto & x+y-z \end{array} \right.\). Alors, \(f\) est une forme linéaire et \(F=\operatorname{Ker}f\). On peut être ici plus précis : \(F\) est le plan vectoriel de vecteur normal \(\left(1,1,-1\right)\).
Soit \(D: \left\{ \begin{array}{ccl} \mathcal{C}^{1}\left(\mathbb{R}\right) & \longrightarrow & \mathcal{C}^{0}\left(\mathbb{R}\right) \newline f & \longmapsto & D\left(f\right)=f' \end{array} \right.\). On a :
\(\operatorname{Ker}D=\left\{f\in \mathcal{C}^{1}\left(\mathbb{R}\right) ~|~ D\left(f\right)=0\right\}\) qui est égal à l’ensemble des fonctions constantes sur \(\mathbb{R}\).
\(\mathop{\rm Im}D=\left\{D\left(f\right) ~|~ f \in
\mathcal{C}^{1}\left(\mathbb{R}\right)\right\}=\mathcal{C}^{0}\left(\mathbb{R}\right)\). Autrement dit, \(D\) est surjective. Démontrons le. Soit \(f\in \mathcal{C}^{0}\left(\mathbb{R}\right)\). Comme \(f\) est continue sur \(\mathbb{R}\) et que \(\mathbb{R}\) est un intervalle, \(f\) possède une primitive \(F:\mathbb{R}\rightarrow \mathbb{R}\). De plus \(F\) est dérivable et sa dérivée \(f\) est continue. Donc \(F\in
\mathcal{C}^{1}\left(\mathbb{R}\right)\). On a bien \(D\left(F\right)=f\) et \(D\) est bien surjective.
(Caractérisation des applications linéaires injectives). Soit \(f:E\rightarrow F\) une application linéaire. Alors : \[\boxed{\textrm{ $f$ est injective si et seulement si }\operatorname{Ker}f=\left\{0_E\right\}}\]
Supposons que \(f\) est injective. Rappelons que comme \(f\) est linéaire, \(f\left(0_E\right)=0_F\). Ainsi \(0_F\) admet donc comme antécédent \(0_E\). Mais \(f\) étant injective \(0_E\) est le seul antécédent de \(0_F\). Il est alors clair que \(\operatorname{Ker}f= \left\{0_E\right\}\).
Réciproquement, supposons que \(\operatorname{Ker}f= \left\{0_E\right\}\) et montrons que \(f\) est injective. Soient \(x_1,x_2\in E\) tels que \(f\left(x_1\right)=f\left(x_2\right)\). Par linéarité de \(f\), on peut écrire que \(f\left(x_1-x_2\right)=0_F\). Donc \(x_1-x_2 \in \operatorname{Ker}f=\left\{0_E\right\}\). Il s’ensuit que \(x_1-x_2=0_E\) et donc que \(x_1=x_2\). \(f\) est donc injective.
On reprend l’exemple précédent, \(D: \left\{ \begin{array}{ccl} \mathcal{C}^{1}\left(\mathbb{R}\right) & \longrightarrow & \mathcal{C}^{0}\left(\mathbb{R}\right) \\ f & \longmapsto & D\left(f\right)=f' \end{array} \right.\) n’est par injective car son noyau contient d’autres fonctions que la fonction nulle, comme par exemple \(f:x\rightarrow 1\).
Soit \(\theta: \left\{ \begin{array}{ccl} \mathbb{R}^2 & \longrightarrow & \mathbb{R}^2 \\ \left(x,y\right) & \longmapsto & \left(x+y,x-y\right) \end{array} \right.\). On vérifie facilement que \(\operatorname{Ker}f=\left\{\left(0,0\right)\right\}\) en résolvant le système \(\begin{cases}x+y=0\newlinex-y=0\end{cases}\) et donc \(f\) est injective.
[Caractérisation des applications linéaires surjectives] Soit \(f:E\rightarrow F\) une application linéaire. Par définition, \(f\) est surjective si et seulement si \(\mathop{\mathrm{Im}}f=F\).
Étude de \(\mathfrak{L}\left(E,F\right)\)
On note \(\mathfrak{L}\left(E,F\right)\) l’ensemble des applications linéaires de \(E\) dans \(F\).
(\(\left(\mathfrak{L}\left(E,F\right),+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel ). Le triplet \(\left(\mathfrak{L}\left(E,F\right),+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel. En particulier, si \(\left(f,g\right)\in \left(\mathfrak{L}\left(E,F\right)\right)^2\) et \(\left(\alpha,\beta\right)\in \mathbb{K}^2\) alors \(\alpha f + \beta g\) est linéaire.
Comme \(F\) est un \(\mathbb{K}\)-espace vectoriel, l’ensemble \(\mathcal F\left(E,F\right)\) des fonctions de \(E\) dans \(F\) a une structure de \(\mathbb{K}\)-espace vectoriel. Pour montrer que \(\mathfrak{L}\left(E,F\right)\) est un \(\mathbb{K}\)-espace vectoriel, il suffit alors de montrer que \(\mathfrak{L}\left(E,F\right)\) est un sous-espace vectoriel de \(\mathscr F\left(E,F\right)\). Il est clair que \(\mathfrak{L}\left(E,F\right)\) est non vide car il contient par exemple l’application identiquement nulle \(f:x\mapsto 0_F\). On vérifie de plus facilement que si \(f,g\in \mathfrak{L}\left(E,F\right)\) alors \(\alpha f + \beta
g\) est linéaire. Donc \(\mathfrak{L}\left(E,F\right)\) est bien un sous-espace vectoriel de \(\mathscr F\left(E,F\right)\).
Étude de \(\mathfrak{L}\left(E\right)\)
On note \(\mathfrak{L}\left(E\right)\) l’ensemble des endomorphismes du \(\mathbb{K}\)-espace vectoriel \(E\).
(\(\left(\mathfrak{L}\left(E\right),+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel.). Le triplet \(\left(\mathfrak{L}\left(E\right),+,\cdot\right)\) est un \(\mathbb{K}\)-espace vectoriel.
C’est une conséquence directe de la proposition précédente car \(\mathfrak{L}\left(E\right)=\mathfrak{L}\left(E,F\right)\)
(La composée de deux applications linéaires est une application linéaire). Soient \(\left(E,+,\cdot\right)\), \(\left(F,+,\cdot\right)\) et \(\left(G,+,\cdot\right)\) trois \(\mathbb{K}\)-espaces vectoriels. Si \(f\in \mathfrak{L}\left(E,F\right)\) et si \(g\in \mathfrak{L}\left(F,G\right)\) alors \(g\circ f \in
\mathfrak{L}\left(E,G\right)\)
La preuve, facile, est laissée en exercice.
(Identité de \(E\)). Soit \(\left(E,+,\cdot\right)\) un \(\mathbb{K}\)-espace vectoriel. On définit la fonction identité de \(E\) par \(Id_E: \left\{ \begin{array}{ccl} E & \longrightarrow & E \newline x & \longmapsto & x \end{array} \right.\).
(Homothétie de \(E\)). Soit \(\left(E,+,\cdot\right)\) un \(\mathbb{K}\)-espace vectoriel. On appelle homothétie vectorielle de rapport \(\lambda\in\mathbb{K}\) l’application \(h_\lambda=\lambda\cdot Id\), \(h_\lambda: \left\{ \begin{array}{ccl} E & \longrightarrow & E \newline x & \longmapsto & \lambda\cdot x \end{array} \right.\).
Ces deux applications sont linéaires et sont donc des endomorphismes de \(E\).
Toute homothétie vectorielle de rapport \(\lambda\neq 0\) est injective.
(\(\left(\mathfrak{L}\left(E\right),+,\circ\right)\) est un anneau unitaire). Le triplet \(\left(\mathfrak{L}\left(E\right),+,\circ\right)\) est un anneau unitaire (généralement non commutatif).
On vérifie facilement que \(\left(\mathfrak{L}\left(E\right),+,\circ\right)\) vérifie les axiomes d’un anneau unitaire.
Étude de \({\rm GL}(E)\)
On note \({\rm GL}(E)\) l’ensemble des automorphismes de \(E\).
(L’inverse d’une application linéaire bijective est linéaire). Soit \(f:E\rightarrow F\) un isomorphisme entre les espaces vectoriels \(E\) et \(F\) alors \(f^{-1}:F\rightarrow
E\) (qui existe car \(f\) est bijective) est aussi linéaire, c’est-à-dire \(f^{-1}\in\mathfrak{L}\left(F,E\right)\).
Soient \(x,x'\in E\) et \(y,y'\in F\) tels que \(y=f\left(x\right)\) et \(y'=f\left(x'\right)\). Soient \(\alpha,\alpha'\in\mathbb{K}\). On a : \[\begin{aligned}
f^{-1}\left(\alpha y + \alpha' y'\right)&=&f^{-1}\left( \alpha f\left(x\right)+\alpha' f\left(x'\right)\right)\\
&=& f^{-1}\left( f \left(\alpha x + \alpha' x'\right)
\right)\textrm{ car $f$ est linéaire}\\
&=& \alpha x + \alpha' x' \newline
&=& \alpha f^{-1}\left(y\right) + \alpha' f^{-1}\left(y'\right)\end{aligned}\] et \(f^{-1}\) est bien linéaire.
(\(\left({\rm GL}(E),\circ\right)\) est un groupe). Le couple \(\left({\rm GL}(E),\circ\right)\) est un groupe (en général non commutatif) d’élément neutre \(Id_E\). On l’appelle groupe linéaire de \(E\).
En utilisant la propriété précédente, on vérifie facilement que \(\mathrm{GL}_{ }(E)\) vérifie les axiomes d’un groupe.
Pour prouver qu’une application \(f:E\rightarrow E\) est bijective on utilise souvent la propriété suivante \(f\) est bijective si et seulement s’il existe \(g:E\rightarrow E\) telle que \(f\circ
g=g\circ f=Id_E\). Dans ce cas, \(g=f^{-1}\).
Soient un \(\mathbb{R}\)-espace vectoriel \(E\) et un endomorphisme \(u\in L(E)\) vérifiant : \(u^3 +u^2 +2\mathop{\mathrm{id}}\nolimits_E = 0\). Montrons que \(u\in {\rm GL}(E)\) et déterminons son inverse \(u^{-1}\). En utilisant la linéarité de \(u\), l’égalité se factorise en \(u\circ{\left[-{\scriptstyle 1\over\scriptstyle 2}\left(u^2+u\right)\right]}=\mathop{\mathrm{id}}\nolimits_E\) ou encore \({-{\scriptstyle 1\over\scriptstyle 2}\left(u^2+u\right)}\circ u=\mathop{\mathrm{id}}\nolimits_E\). Donc \(u\) est inversible et \(u^{-1}=-{\scriptstyle 1\over\scriptstyle 2}\left(u^2+u\right)\).
Équations linéaires
Définitions
On va expliquer dans cette section que l’ensemble des solutions d’un système linéaire ou d’une équation différentielle linéaire sont équipés d’une même structure.
(Équations linéaires). On appelle équation linéaire une équation de la forme \(u\left(x\right)=b\) où :
\(u\) est une application linéaire définie entre un \(\mathbb{K}\)-espace vectoriel E et un \(\mathbb{K}\)-espace vectoriel F : \(u\in\mathfrak{L}\left(E,F\right)\).
\(b\) est un vecteur de \(F\) appelé second membre de l’équation.
L’inconnue \(x\) est à valeurs dans \(E\).
Soient \(E=\mathbb{K}^n\), \(F=\mathbb{K}^m\), \(x=\left(x_1,\dots,x_n\right)\) et \(b=\left(b_1,\dots,b_m\right)\). Soit \[u: \left\{ \begin{array}{ccl} E & \longrightarrow & F \\ x=\left(x_1,\dots,x_n\right) & \longmapsto & \left(\begin{array}{c}
a_{11}x_1+\dots+a_{1n}x_n\\
a_{21}x_1+\dots+a_{2n}x_n\\
\vdots \\
a_{m1}x_1+\dots+a_{mn}x_n
\end{array}\right) \end{array} \right.\] Alors \(u\) est linéaire et l’équation \(u\left(x\right)=b\) est équivalente au système d’équations : \[\begin{cases}
a_{11}x_1+\dots+a_{1n}x_n=b_1\\
a_{21}x_1+\dots+a_{2n}x_n=b_2\\
\quad \quad~~\quad\vdots \quad \\
a_{m1}x_1+\dots+a_{mn}x_n=b_n
\end{cases}\]
Soient \(E=\mathcal{C}^{1}\left(\mathbb{R},\mathbb{R}\right)\), \(F=\mathcal{C}^{0}\left(\mathbb{R},\mathbb{R}\right)\), \(a,b\in
\mathcal{C}^{0}\left(\mathbb{R},\mathbb{R}\right)\) et \[\theta: \left\{ \begin{array}{ccl} E & \longrightarrow & F \\ \varphi & \longmapsto & a\varphi'+b\varphi \end{array} \right. .\] Soit \(c\in F\). L’équation linéaire \(\theta\left(\varphi\right)=c\) d’inconnue \(\varphi\in\mathcal{C}^{1}\left(\mathbb{R},\mathbb{C}\right)\) est une équation différentielle du premier degré.
Soient \(E=\mathcal{C}^{2}\left(\mathbb{R},\mathbb{C}\right)\), \(F=\mathcal{C}^{0}\left(\mathbb{R},\mathbb{C}\right)\), \(a,b,c\in
\mathbb{C}\) et \[\theta: \left\{ \begin{array}{ccl} E & \longrightarrow & F \newline \varphi & \longmapsto & a\varphi''+b\varphi'+c\varphi \end{array} \right.\] Soit \(d\in
F\). L’équation linéaire \(\theta\left(\varphi\right)=c\) d’inconnue \(\varphi\in\mathcal{C}^{2}\left(\mathbb{R},\mathbb{C}\right)\) est une équation différentielle du second degré à coefficients constants.
Structure de l’ensemble des solutions
Les-mathematiques.net
(Structure de l’ensemble des solutions d’une équation linéaire). Soient \(E\) et \(F\) deux \(\mathbb{K}\)-espaces vectoriels, \(u\in\mathfrak{L}\left(E,F\right)\) et \(b\in F\). On note \(\mathcal S\) l’ensemble des solutions de l’équation linéaire \(u\left(x\right)=b\) et \(\mathcal S_0\) l’ensemble des solutions de l’équation sans second membre :\(u\left(x\right)=0\). On a :
\(\mathcal S_0\) est un sous-espace vectoriel de \(E\) (et donc \(\mathcal S_0\) est non vide!).
Si \(S\neq \varnothing\) et si \(x_0\in S\) alors \(S=\left\{x_0+h ~|~
h\in S_0\right\}=x_0+S_0\)
L’ensemble \(\mathcal S_0\) est le noyau de \(u\), c’est donc un sous-espace vectoriel de \(E\) d’après le théorème [theo_ker_im_sev] page [theo_ker_im_sev]. Soit \(x_0\in S\), c’est-à-dire un élément \(x_0\) de \(E\) tel que \(u\left(x_0\right)=b\). Montrons que \(S=\left\{x_0+h
~|~ h\in S_0\right\}\). Pour ce faire, effectuons un raisonnement par double inclusion :
Soit \(x\in S\). Alors \(u\left(x-x_0\right)=u\left(x\right)-u\left(x_0\right)=b-b=0\). Donc \(x-x_0=h \in S_0\) et \(x=x_0+h\) avec \(h\in S_0\) et \(x\in x_0+S_0\).
Soit \(h\in S_0\). On a \(u\left(x_0 +
h\right)=u\left(x_0\right)+u\left(h\right)=b\) et donc \(x_0 + h \in S\).
\(E\) désigne là encore un \(\mathbb{K}\)-espace vectoriel.
Projecteurs
Les-mathematiques.net
Projection sur \(E_1\) parallèlement à \(E_2\)
(Projecteurs). Soient \(E_1\) et \(E_2\) deux sous-espaces vectoriels supplémentaires de \(E\) : \(E=E_1\oplus E_2\). Pour tout \(x\in E\), il existe donc un unique couple \(\left(x_1,x_2\right)\in E_1\times E_2\) tel que \(x=x_1+x_2\). Soit \[p: \left\{ \begin{array}{ccl} E & \longrightarrow & E \newline x=x_1+x_2 & \longmapsto & x_1 \end{array} \right.\] L’application \(p\) est bien définie et est appelée projecteur de \(E\) sur \(E_1\) parallèlement à \(E_2\).
(Propriétés des projecteurs). Soient \(E_1\) et \(E_2\) deux sous-espaces vectoriels supplémentaires de \(E\) : \(E=E_1\oplus E_2\) et soit \(p\) le projecteur de \(E\) sur \(E_1\) parallèlement à \(E_2\) alors :
\(p\) est linéaire : \(p\in\mathfrak{L}\left(E\right)\).
\(\operatorname{Ker}p=E_2\).
\(\mathop{\mathrm{Im}}p=E_1\).
\(p\left(x\right)=x \Longleftrightarrow x\in E_1\) (\(E_1\) est l’ensemble des vecteurs invariants par \(p\)).
Soient \(x=x_1+x_2\in E_1\oplus E_2=E\) et \(x'= x'_1+x'_2\in E_1\oplus
E_2=E\) ainsi que deux scalaires \(\alpha,\alpha'\in \mathbb{K}\). On a : \[\alpha x +
\alpha ' x'=\underbrace{\left(\alpha x_1 + \alpha ' x'_1 \right)}_{\in E_1} +
\underbrace{\left(\alpha x_2 + \alpha ' x'_2 \right)}_{\in E_2}\in E_1\oplus E_2.\] et : \[\begin{aligned}
p\left(\alpha x + \alpha ' x'\right) &=& \alpha x_1 + \alpha ' x'_1\\
&=& \alpha p\left(x\right) + \alpha'p\left(x'\right)\end{aligned}\] ce qui prouve que \(p\) est linéaire.
Soient \(x=x_1+x_2\in E_1\oplus E_2=E\). On a : \[p\left(x\right)=0 \Longleftrightarrow x_1=0 \Longleftrightarrow
x=x_2 \Longleftrightarrow x\in E_2.\] Par conséquent : \(\operatorname{Ker}p=E_2\).
Soient \(x=x_1+x_2\in E_1\oplus E_2=E\). On a : \[\begin{aligned}
x\in \mathop{\mathrm{Im}}p &\Longleftrightarrow& \exists x'=x'_1+x'_2\in E_1\oplus E_2:\quad
x=p\left(x'\right) \\
&\Longleftrightarrow& x=x'_1\in E_1 \newline
&\Longleftrightarrow& x\in E_1.\end{aligned}\] Donc \(\mathop{\mathrm{Im}}p=E_1\).
Soit \(x=x_1+x_2\in E_1\oplus E_2=E\). On a : \[p\left(x\right)=x\Longleftrightarrow x=x_1 \Longleftrightarrow
x\in E_1\]
(Caractérisation des projecteurs). Soit \(p\in\mathfrak{L}\left(E\right)\). Alors \(p\) est un projecteur si et seulement si \(\boxed{p\circ p=p}\) (c’est-à-dire si et seulement si \(p\) est idempotente).
Dans ce cas, \(p\) est le projecteur sur \(\operatorname{Ker}p\) parallèlement à \(\mathop{\mathrm{Im}}p\).
Si \(p\) est un projecteur et si \(x\in E\), alors en appliquant la proposition précédente, \(p\left(x\right)\in E_1\) et comme \(E_1\) est stable par \(p\), \(p\left(p\left(x\right)\right)=p\left(x\right)\). Donc \(p\circ p=p\).
Réciproquement, si \(p\) est un endomorphisme de \(E\) vérifiant \(p\circ p=p\) : posons \(E_1=\mathop{\mathrm{Im}}p\) et \(E_2=\operatorname{Ker}p\) et montrons que ces deux sous-espaces vectoriels de \(E\) sont supplémentaires dans \(E\).
Soit \(x\in E_1\cap E_2\). Alors, on a à la fois \(p\left(x\right)=0\) car \(x\in
E_2=\operatorname{Ker}p\) et \(x=p\left(x'\right)\) où \(x'\in E\) car \(x\in E_1=\mathop{\mathrm{Im}}p\). Par conséquent : \(0=p\left(x\right) = p\left(p\left(x'\right)\right)\). Mais comme \(p\circ p=p\), on a \(p\left(p\left(x'\right)\right)=p\left(x'\right)=x\) et donc \(x=0\), ce qui prouve que \(E_1\) et \(E_2\) sont en somme directe.
Soit \(x\in E\). On a : \[x= \underbrace{p\left(x\right)}_{=x_1} +
\underbrace{\left(x-p\left(x\right)\right)}_{=x_2}\] et \(x_1\in E_1\) (car \(x_1=p\left(x\right)\in\mathop{\mathrm{Im}}
p\)) et \(x_2\in E_2\) (car \(p(x_2)=p\left({x-p\left(x\right)}\right)=p(x)-p^2(x)=p(x)-p(x)=0\)). Par conséquent : \(E=E_1+E_2\)
Donc \(E=E_1\oplus E_2\). Si \(x=x_1+x_2\in E_1\oplus E_2=E\), comme \(x_1\in E_1\), \(p\left(x_1\right)=x_1\) et comme \(x_2\in E_2\), \(p\left(x_2\right)=0\). Par linéarité de \(p\), \(p\left(x\right)=p\left(x_1\right)+p\left(x_2\right)=x_1\). \(p\) est donc bien le projecteur de \(E\) sur \(E_1\) parallèlement à \(E_2\).
Si \(E=E_1 \oplus E_2\), si \(p\) est le projecteur de \(E\) sur \(E_1\) parallèlement à \(E_2\) et si \(q\in\mathfrak{L}\left(E\right)\) alors on a équivalence entre :
\(q\) est le projecteur de \(E\) sur \(E_2\) parallèlement à \(E_1\).
\(\boxed{p+q=\mathop{\mathrm{id}}\nolimits_E}\).
Supposons que \(q\) est le projecteur de \(E\) sur \(E_2\) parallèlement à \(E_1\). Si \(x=x_1+x_2\in E_1\oplus E_2\) alors \(p\left(x\right)=x_1\) et \(q\left(x\right)=x_2\). Donc \(x=p\left(x\right)+q\left(x\right)\) et on a bien \(p+q=\mathop{\mathrm{id}}\nolimits_E\).
Réciproquement, si \(p+q=\mathop{\mathrm{id}}\nolimits_E\) et si \(x=x_1+x_2\in E_1\oplus E_2\) alors \(q\left(x\right)=x-x_1=x_2\) donc \(q\) est le projecteur de \(E\) sur \(E_2\) parallèlement à \(E_1\).
Symétries
Les-mathematiques.net
Symétrie par rapport à \(E_1\) parallèlement à \(E_2\)
(Symétries). Soient \(E_1\) et \(E_2\) deux sous-espaces vectoriels supplémentaires de \(E\) : \(E=E_1\oplus E_2\). Pour tout \(x\in E\), il existe donc un unique couple \(\left(x_1,x_2\right)\in E_1\times E_2\) tel que \(x=x_1+x_2\). Soit \[s: \left\{ \begin{array}{ccl} E & \longrightarrow & E \newline x=x_1+x_2 & \longmapsto & x_1-x_2 \end{array} \right.\]\(s\) est bien définie et est appelée symétrie par rapport à \(E_1\) parallèlement à \(E_2\), ou plus simplement symétrie.
(Propriétés des symétries). Soient \(E_1\) et \(E_2\) deux sous-espaces vectoriels supplémentaires de \(E\) : \(E=E_1\oplus E_2\) et soit \(s\) la symétrie par rapport à \(E_1\) parallèlement à \(E_2\), alors :
L’application \(s\) est linéaire : \(s\in\mathfrak{L}\left(E\right)\).
Si \(p\) est le projecteur de \(E\) sur \(E_1\) parallèlement à \(E_2\) alors \(\boxed{s=2p-Id_E}\).
\(s\) est involutive, c’est-à-dire : \(s\circ s=Id_E\).
Soit \(p\) le projecteur de \(E\) sur \(E_1\) parallèlement à \(E_2\). Soit \(x=x_1+x_2\in E_1\oplus E_2=E\). On a : \(p\left(x\right)=x_1\) et \[\left(2p-Id_E\right)\left(x\right)=2p\left(x\right)-x=2x_1-\left(x_1+x_2\right)=x_1-x_2=s\left(x\right)\] ce qui démontre le second point. Comme \(p\) est linéaire et qu’une combinaison linéaire d’ applications linéaires est linéaire, \(s\) est linéaire et le premier point est aussi démontré. Enfin, en utilisant la linéarité et l’idempotence de \(p\) : \[\begin{aligned}
s\circ s &=& \left(2p-Id_E\right)\circ \left(2p-Id_E\right) \\
&=& 2p\circ\left(2p-Id_E\right) - \left(2p-Id_E\right) \\
&=& 4p^2-2p- 2p+Id_E\\
&=&4p-4p+Id_E\newline
&=&Id_E\end{aligned}\] et le troisième point est démontré.
(Caractérisation des symétries). Soit \(s\in\mathfrak{L}\left(E\right)\). Si \(s\) est involutive, c’est-à-dire si \(\boxed{s\circ s=Id_E}\), alors \(s\) est la symétrie par rapport à \(E_1=\operatorname{Ker}\left(s-Id_E\right)\) et parallèlement à \(E_2=\operatorname{Ker}{\left(s+Id_E\right)}\)).
Supposons que \(s\) est linéaire et involutive. Posons \(E_1=\operatorname{Ker}\left(s-Id_E\right)\) et \(E_2=\operatorname{Ker}{\left(s+Id_E\right)}\). Montrons que ces deux sous-espaces vectoriels de \(E\) sont supplémentaires dans \(E\).
Soit \(x\in E_1\cap E_2\). On a donc : \(s\left(x\right)-x=0\) et \(s\left(x\right)+x=0\). Soustrayant ces deux égalités, on obtient \(x=0\), donc \(E_1\) et \(E_2\) sont en somme directe
Soit \(x\in E\). On a : \[x= \underbrace{-\dfrac{1}{2}\left(s\left(x\right)-x\right)}_{\in E_1} + \underbrace{\dfrac{1}{2}\left(s\left(x\right)+x\right)}_{\in E_2}\] et donc \(E=E_1+E_2\).
On en déduit que \(E=E_1 \oplus E_2\). De plus, si \(x=x_1+x_2\in E_1\oplus E_2=E\) alors : comme \(x_1\in E_1\), on a : \(s\left(x_1\right)=x_1\) et comme \(x_2\in E_2\), on a aussi : \(s\left(x_2\right)=-x_2\). Par linéarité de \(s\), on en déduit que : \(s\left(x\right)=s\left(x_1\right)+s\left(x_2\right)=x_1-x_2\). L’application \(s\) est donc bien la symétrie par rapport à \(E_1\) et parallèlement à \(E_2\)
[Décomposition associée à un projecteur]
Les-mathematiques.net
[Décomposition associée à une symétrie]
Les-mathematiques.net
En résumé
Les différentes définitions de ce chapitre doivent être connues avec la plus grande précision.
Vous devez être capable de donner différents exemples d’espace vectoriels, de sous-espaces vectoriels, de sous-espaces supplémentaires. Il faudra passer du temps à reprendre les différents exemples de ce chapitre.
Les notions de projecteurs et symétries doivent être bien assimilées.
Ne vous découragez pas. Les premiers pas en algèbre linéaire sont souvent difficiles. Le temps et le travail aidant, ces nouvelles notions vont vite s’éclaircir.
Bibliographie
Barre utilisateur
[ID: 76] [Date de publication: 28 décembre 2021 17:31] [Catégorie(s): Le cours de SUP ] [
Nombre commentaires: 0] [nombre d'éditeurs:
1 ] [Editeur(s): Emmanuel Vieillard-Baron ]
[nombre d'auteurs:
3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]
Les-mathematiques.net
