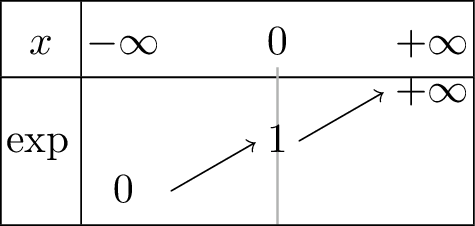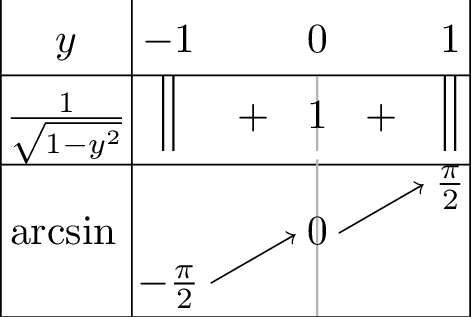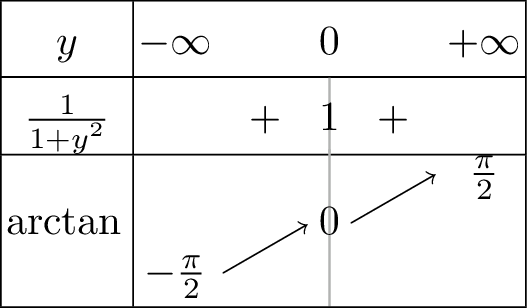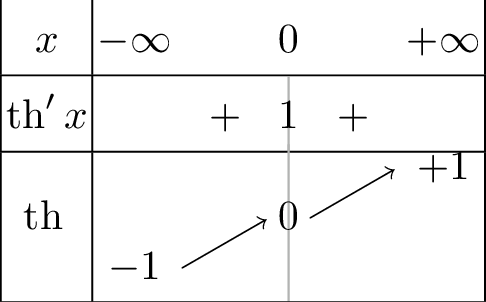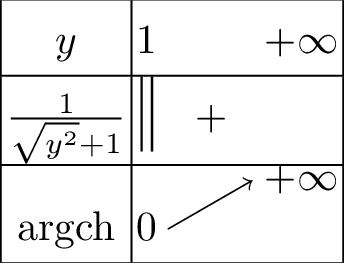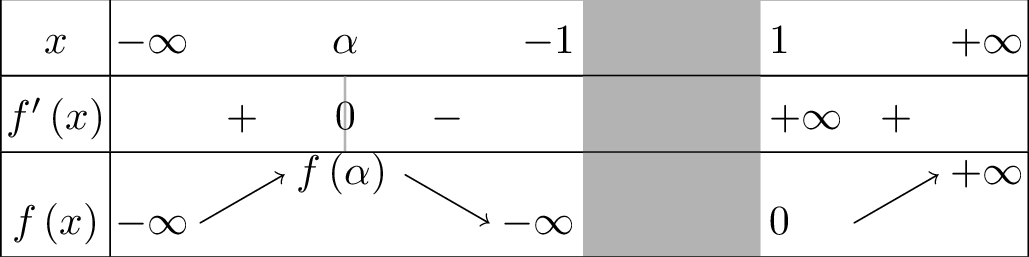Nous commençons ce chapitre par quelques généralités sur les fonctions. Nous introduisons en particulier les notions de monotonie, de parité et de périodicité. Puis nous effectuons quelques rappels d’analyse du lycée. Nous expliquons sans la formaliser la notion de limite puis celles de continuité et de dérivabilité. Nous terminons cette section par un paragraphe sur l’intégration. Nous ne proposons aucune preuve, il est trop tôt pour cela, elles viendront plus tard dans l’année. L’idée est d’introduire les outils de base en analyse afin de pouvoir en disposer dés le début d’année et de préparer ainsi les chapitres ultérieurs dans lesquels ces notions seront approfondies.
Fonctions usuelles
Nous continuons ce chapitre en introduisant les différentes fonctions usuelles en
Pour bien aborder ce chapitre
Our federal income tax law defines the tax \(y\) to be paid in terms of the income \(x\); it does so in a clumsy enough way by pasting several linear functions together, each valid in another interval or bracket of income. An archeologist who, five thousand years from now, shall unearth some of our income tax returns together with relics of engineering works and mathematical books, will probably date them a couple of centuries earlier, certainly before Galileo and Vieta. Weyl, Hermann ; The mathematical way of thinking
L’objet de ce chapitre est d’introduire les différentes fonctions utilisées de manière usuelles en
Nous utiliserons à plusieurs reprises dans ce chapitre des théorèmes qui ne seront énoncés et démontrés que beaucoup plus tard dans l’année. Parmi ces théorèmes, notons les trois suivants :
continue sur \(I\).
strictement monotone sur \(I\).
\(f\) est strictement monotone sur l’intervalle \(I\).
\(f\) est dérivable sur \(I\).
\(\forall x\in I, \quad f'\left(x\right)\neq 0\)
\(f\) est dérivable sur un intervalle \(I\).
On retrouvera le premier théorème et sa démonstration en [theo_bij_continue] page [theo_bij_continue] et le second en [derivee_non_nulle_implique_bij] page [derivee_non_nulle_implique_bij]. Le troisième sera établi en [carac_fcts_constantes_ou_monotones] page [carac_fcts_constantes_ou_monotones].
Multimédia: Traceur de courbe réciproque: on donne le graphe d’une fonction. On pointe sur un point du graphe et on obtient son symétrique par rapport à la bissectrice principale. On affiche le vecteur tangent en ce point au graphe initial et on obtient le vecteur tangent au graphe de la réciproque correspondant. En cliquant sur un bouton, on affiche le graphe entier de la réciproque.
Fonctions logarithmes, exponentielles et puissances
Logarithme népérien
Nous verrons au chapitre [chap_integration] dans le théorème [continue_implique_primitive] page [continue_implique_primitive] que toute fonction continue sur un intervalle \(I\) de \(\mathbb{R}\) possède une primitive sur cet intervalle (voir [continue_implique_primitive]). La fonction \(x \mapsto \dfrac{1}{x}\) définie sur \(\mathbb{R}_+^*\) admet donc une primitive sur \(\mathbb{R}_+^*\). On pourrait montrer, mais c’est difficile, que l’on ne peut exprimer cette primitive avec des fonctions usuelles (fonctions polynomiales, fractions rationnelles, fonctions trigonométriques). Il faut donc introduire une nouvelle fonction.
La fonction \(\ln\) est continue sur \(\mathbb{R}_+^*\).
La fonction \(\ln\) est dérivable sur \(\mathbb{R}_+^*\) et \(\boxed{\forall x\in\mathbb{R}_+^*, \quad \ln' x=\dfrac{1}{x}}\).
La fonction \(\ln\) est même \(\mathcal{C}^{\infty}\) sur \(\mathbb{R}_+^*\), ce qui signifie qu’elle est dérivable et que toutes ses dérivées sont dérivables.
La fonction \(\ln\) est concave sur \(\mathbb{R}_+^*\)
\(\boxed{\ln\left(xy\right)=\ln x+\ln y}\)
\(\boxed{\ln\left(\dfrac{1}{x}\right)=-\ln x}\)
\(\boxed{\ln\left(\dfrac{x}{y}\right)=\ln x-\ln y}\)
\(\boxed{\ln \left(x^n\right)=n\ln x}\)
La méthode pour prouver cette égalité est classique, il faut la retenir. Fixons \(y\in\mathbb{R}_+^*\) et notons \(\theta_y\) la fonction \[\theta_y: \left\{ \begin{array}{ccl} \mathbb{R}_+^* & \longrightarrow & \mathbb{R} \newline x & \longmapsto & \ln\left(xy\right)-\ln x - \ln y \end{array} \right. .\] Cette fonction est dérivable sur \(\mathbb{R}_+^*\) comme composée et différence de fonctions dérivables. De plus, \[\forall x\in \mathbb{R}_+^*,\quad \theta_y'\left(x\right)=\dfrac{y}{xy}-\dfrac{1}{x}=\dfrac{1}{x}-\dfrac{1}{x}=0.\] D’après le théorème [carac_fcts_constantes_fcts_usuelles], \(\theta_y\) est une fonction constante sur \(\mathbb{R}_+^*\). Elle est donc constante sur \(\mathbb{R}_+^*\) et il existe \(c\in\mathbb{R}\) tel que : \(\forall x\in \mathbb{R}_+^*, \quad \theta_y\left(x\right)= c\). Déterminons cette constante. \(c=\theta_y\left(1\right)=\ln y -\ln 1 - \ln y = 0\). Ce qui prouve que, pour tout \(x\) dans \(\mathbb{R}_+^*\), \(\theta_p\left(x\right)=\ln\left(xy\right)-\ln x + \ln y=0\).
Soit \(x\in\mathbb{R}_+^*\). Par application de la proposition précédente, on a les égalités \[0=\ln 1 = \ln\left(\dfrac{x}{x}\right)=\ln\left(x . \dfrac{1}{x}\right)=\ln x + \ln\dfrac{1}{x}.\] desquelles découlent le résultat.
Soient \(x,y\in\mathbb{R}_+^*\), par application des deux dernières égalités \[\ln \left(\dfrac{x}{y}\right) = \ln\left(x . \dfrac{1}{y}\right)=\ln x + \ln\dfrac{1}{y}=\ln x - \ln y.\]
Par récurrence.
La fonction \(ln\) est strictement croissante et \(\ln 1=0\), donc \(\ln 2>0\). D’après la dernière égalité de la proposition précédente, pour tout \(n\in\mathbb{N}\), on peut écrire \(\ln \left(2^n\right)=n\ln 2\). On en déduit que \(\ln \left(2^n\right)\xrightarrow[n\rightarrow +\infty]{}+\infty\). La fonction \(\ln\) n’est donc pas majorée. Comme elle est strictement croissante, on peut affirmer, par application du théorème de la limite monotone [theo_de_la_limite_monotone_pour_les_fonctions], que \(\ln x \xrightarrow[x\rightarrow +\infty]{} +\infty\).
Par application du théorème d’opérations sur les limites et par utilisation de la limite précédente, \[\ln x=-\ln\dfrac{1}{x}\xrightarrow[x\rightarrow 0^+]{}-\infty.\]
\(\ln x \textrm{ est négligeable devant }x \textrm{ quand }x \textrm{ tend vers } +\infty\) : \(\boxed{\dfrac{\ln x}{x}\xrightarrow[x\rightarrow +\infty]{} 0 }\).
\(\ln x \textrm{ est négligeable devant }\dfrac{1}{x} \textrm{ quand }x \textrm{ tend vers } 0\) : \(\boxed{x\ln x\xrightarrow[x\rightarrow 0^+]{} 0 }\).
Pour tout \(t\geqslant 1\), on a \(\dfrac{1}{t} \leqslant\dfrac{1}{\sqrt t}\). Fixons \(x\geqslant 1\). Il vient que \(\int_{1}^{x} {\scriptstyle\textrm{ d}t\over\scriptstyle t} \leqslant\int_{1}^{x} {\scriptstyle\textrm{ d}t\over\scriptstyle{\sqrt t}}\) ce qui s’écrit aussi \(\ln x \leqslant 2\left(\sqrt x-1\right) \leqslant 2\sqrt x\). Divisant cette inégalité par \(x\), on obtient \(0\leqslant\dfrac{\ln x}{x}\leqslant\dfrac{2}{\sqrt x}\) ce qui amène, par application du théorème des gendarmes [theo_des_gendarmes_pour_les_fcts], \(\dfrac{\ln x}{x}\xrightarrow[x\rightarrow +\infty]{} 0\).
Par ailleurs : \(X\ln X\xlongequal{x=1/X}-\dfrac{\ln x}{x}\xrightarrow[X\rightarrow +\infty]{}0\).
La fonction \(ln\) est dérivable en \(1\) et \(\ln ' 1=1\) \(\boxed{\dfrac{\ln\left(x\right)}{x-1} \xrightarrow[x\rightarrow 1]{} 1 }\).
Cette limite s’écrit aussi sous la forme \(\boxed{\dfrac{\ln\left(1+x\right)}{x} \xrightarrow[x\rightarrow 0]{} 1}\).
Le taux d’accroissement de \(\ln\) en \(1\) est donné par : \[\forall x\in \mathbb{R}_+^*\setminus \left\{1\right\},\quad \Delta\left(x\right)=\dfrac{\ln x - \ln 1}{x - 1}=\dfrac{\ln x }{x - 1}.\] Comme \(\ln\) est dérivable en \(x=1\) et que \(\ln' 1 = \dfrac{1}{1}=1\), on a bien \(\displaystyle{\lim_{x \rightarrow 0}\Delta\left(x\right)}=1.\)
La seconde égalité se prouve grâce à un changement de variable :\(\dfrac{\ln\left(x\right)}{x-1}\xlongequal{X=x-1} {\dfrac{\ln\left(1+X\right)}{X}}\xrightarrow[X\rightarrow 0]{}1\)
Exponentielle népérienne
\[\exp: \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R}_+^* \\ y & \longmapsto & \exp y \end{array} \right.\]
\[\begin{aligned} \forall x\in\mathbb{R}_+^*,\quad \boxed{\exp\left(\ln x\right)=x}\\ \forall y\in\mathbb{R}, \quad \boxed{\ln\left(\exp y\right)=y}\end{aligned}\]
La fonction \(\exp\)
est strictement croissante et strictement positive.
est continue \(\mathbb{R}\).
est dérivable sur \(\mathbb{R}\) et \(\forall x\in\mathbb{R}, \boxed{\exp'\left(x\right)=\exp\left(x\right)}\).
dérivable sur \(\mathbb{R}_+^*\).
de dérivée strictement positive sur \(\mathbb{R}_+^*\)
donc strictement croissante sur \(\mathbb{R}_+^*\)
Par application du
\(\boxed{\exp\left(x+y\right)=\exp\left(x\right)\exp\left(y\right)}\)
\(\boxed{\exp\left(-x\right)=\dfrac{1}{\exp x}}\)
\(\boxed{\exp\left(x-y\right)=\dfrac{\exp\left(x\right)}{\exp\left(y\right)}}\)
\(\boxed{\exp\left(nx\right)=\left(\exp \left(x\right)\right)^n}\)
\(\exp{x}\) est prépondérant devant \(x\) quand \(x\) tend vers \(+\infty\) : \(\boxed{\dfrac{\exp x}{x} \xrightarrow[x\rightarrow +\infty]{} +\infty}\).
\(\exp{x}\) est négligeable devant \(\dfrac{1}{x}\) quand \(x\) tend vers \(-\infty\) : \(\boxed{x\exp x \xrightarrow[x\rightarrow -\infty]{} 0}\).
\(\exp{x}\) est dérivable en \(x=0\) de dérivée égale à \(1\) : \(\boxed{\dfrac{\exp x-1}{x} \xrightarrow[x\rightarrow 0]{} 1}\).
Comme \({\scriptstyle\exp x\over\scriptstyle x}\xlongequal{{x=\ln X}} {\scriptstyle X\over\scriptstyle\ln X}={\scriptstyle 1\over\scriptstyle{\scriptstyle\ln X\over\scriptstyle X}}\), il vient \(\displaystyle{\lim_{x \rightarrow +\infty}{\scriptstyle\exp x\over\scriptstyle x}}=\displaystyle{\lim_{X \rightarrow 0^+}{\scriptstyle 1\over\scriptstyle{\scriptstyle\ln X\over\scriptstyle X}}}=+\infty\).
La seconde limite se démontre de la même façon.
Écrivons le taux d’accroissement \(\Delta\) de \(\exp\) en \(0\). Pour tout \(x\in \mathbb{R}^*\) \[\Delta\left(x\right)=\dfrac{\exp x - \exp 0}{x - 0}=\dfrac{\exp x - 1}{x}.\] Comme \(\exp\) est dérivable en \(0\) et que \(exp'\left(0\right)=\exp\left(0\right)=1\), \(\Delta\left(x\right)\xrightarrow[x\rightarrow 0]{} 1\) et la dernière limite est prouvée.
Logarithme de base quelconque
Si \(a=10\), on obtient le logarithme décimal qu’on note \(log\).
Si \(a=e\), \(\log_a =\ln\).
\(\log_a 1=0\) et \(\log_a a = 1\).
\(\log_a \left(xy\right)=\log_a x+\log_a y\)
\(\log_a \left(\dfrac{1}{x}\right)=-\log_a x\)
\(\log_a \left(\dfrac{x}{y}\right)=\log_a x-\log_a y\)
\(\log_a x^n=n\log_a x\)
Si \(a\in]1;+\infty[\), \(\log_a\) est strictement croissante et concave.
Si \(a\in]0;1[\), \(\log_a\) est strictement décroissante et convexe.
Si \(a\in]1;+\infty[\), alors \(\ln a>0\), \(\log_a'\) est donc strictement positive et \(\log_a''\) est strictement négative. Donc \(\log_a\) est strictement croissante et concave.
Si \(a\in]0;1[\), alors \(\ln a<0\), \(\log_a'\) est donc strictement négative et \(\log_a''\) est strictement positive. Donc \(\log_a\) est strictement décroissante et convexe.
Exponentielle de base \(a\)
est dérivable sur \(\mathbb{R}_+^*\).
possède une dérivée sur \(\mathbb{R}_+^*\) strictement positive si \(a\in]1;+\infty[\) et strictement négative si \(a\in]0;1[\)
et est donc strictement croissante sur \(\mathbb{R}_+^*\) si \(a\in]1;+\infty[\) et strictement décroissante sur \(\mathbb{R}_+^*\) si \(a\in]0;1[\).
\(\exp_a 0=1\) et \(\exp_a 1=a\)
\(\exp_a \left(x+y\right)=\exp_a \left(x\right)\exp_a \left(y\right)\)
\(\exp_a \left(x-y\right)=\dfrac{\exp_a \left(x\right)}{\exp_a \left(y\right)}\)
\(\exp_a \left(nx\right)=\left(\exp_a x\right)^n\)
\(\exp_a x \exp_b x = \exp_{ab} x\)
\(\dfrac{\exp_a x}{\exp_b x} = \exp_{{\scriptstyle a\over\scriptstyle b}} x\)
On retrouve la notation précédente \(\exp x = e^x\).
Remarquons aussi que \(1^x=\exp\left( x \ln 1\right) =1.\)
Avec ces notations, la propriété précédente devient :
\(a^0=1\) et \(a^1=a\)
\(a^{x+y}=a^{x} a^{y}\)
\(a^{x-y}=\dfrac{a^{x}}{a^{y}}\)
\(a^{nx}=\left(a^x\right)^n\)
\(\left(ab\right)^x=a^x b^x\)
\(\left(\dfrac{a}{b}\right)^x=\dfrac{a^x}{b^x}\)
Fonctions puissances
\(\varphi_0\) est la fonction constante égale à \(1\).
\(\varphi_1=Id\). algébriques
Pour tout \(a,b\in\mathbb{R}\), \(x,y\in\mathbb{R}_+^*\)
\(x^{a+b}=x^a x^b\)
\(x^{-a}=\dfrac{1}{x^a}\)
\(\left(xy\right)^a=x^a y^a\)
\(\left(x^a\right)^b=x^{ab}\)
\(x^0=1\)
\(1^a=1\)
\(\ln\left(x^a\right)=a\ln x\)
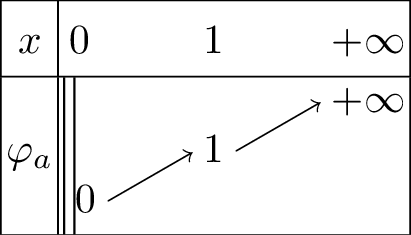
continue \(\mathbb{R}_+^*\).
dérivable sur \(\mathbb{R}_+^*\) et \(\forall x\in\mathbb{R}_+^*, \quad \varphi_a'\left(x\right)=a x^{a-1}\).
De plus,
si \(a>0\), \(\varphi_a\) est croissante, \(\varphi_a\left(x\right)\xrightarrow[x\rightarrow 0^+]{}0\) et \(\varphi_a\left(x\right)\xrightarrow[x\rightarrow +\infty]{}+\infty\).
Si \(a=0\), \(\varphi_a:x\rightarrow x^0=1\) est constante.
Si \(a<0\), \(\varphi_a\) est décroissante, \(\varphi_a\left(x\right)\xrightarrow[x\rightarrow 0^+]{}+\infty\) et \(\varphi_a\left(x\right)\xrightarrow[x\rightarrow +\infty]{}+\infty\).
Si \(a>1\) ou si \(a<0\), \(\varphi_a\) est convexe et si \(0<a<1\), \(\varphi_a\) est concave.
Si \(a>0\), \(a\ln x \xrightarrow[x\rightarrow +\infty]{} +\infty\) et par composition de limite : \(x^a=\exp\left(a \ln x\right)\xrightarrow[x\rightarrow +\infty]{} +\infty\).
Si \(a=0\), \(0=a\ln x \xrightarrow[x\rightarrow +\infty]{}0\) et : \(x^a=x^0=1\xrightarrow[x\rightarrow +\infty]{} 1\).
Si \(a<0\), \(a\ln x \xrightarrow[x\rightarrow +\infty]{} -\infty\) et par composition de limite : \(x^a=\exp\left(a \ln x\right)\xrightarrow[x\rightarrow +\infty]{} 0\).
Si \(a>0\), on peut prolonger \(\varphi_a\) par continuité en \(0\) en posant \(\varphi_a(0)=0\).
Si \(a>1\), \(\varphi_a\) est même dérivable en \(0\): \(\varphi_a'(0)=0\).
Si \(0<a<1\), \(\varphi'_a(x) \xrightarrow[x\rightarrow 0]{} +\infty\) et le graphe de \(\varphi_a\) possède une tangente verticale à l’origine.
Comparaison des fonctions logarithmes, puissances et exponentielles
Fonctions circulaires réciproques
Rappels succincts sur les fonctions trigonométriques
Effectuons un rappel sur les fonctions trigonométriques.
définie sur \(\mathbb{R}\).
à valeurs dans \(\left[-1,1\right]\).
impaire.
\(2\pi\)-périodique.
continue sur \(\mathbb{R}\).
dérivable sur \(\mathbb{R}\) et \[\boxed{\forall x\in\mathbb{R}, \quad \sin' x=\cos x}\]
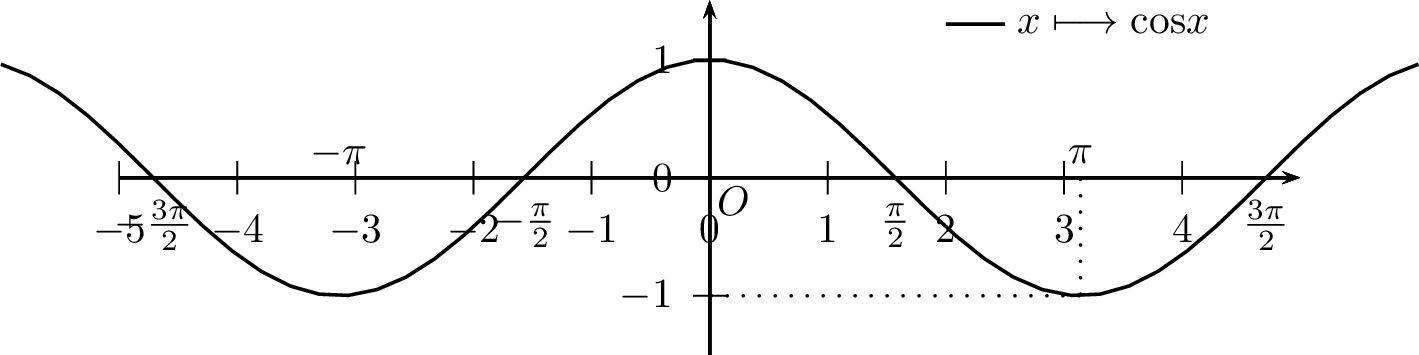
La fonction cosinus, notée \(\cos\) est :
définie sur \(\mathbb{R}\).
à valeurs dans \(\left[-1,1\right]\).
paire.
\(2\pi\)-périodique.
continue sur \(\mathbb{R}\).
dérivable sur \(\mathbb{R}\) et \[\boxed{\forall x\in\mathbb{R}, \quad \cos' x=-\sin x}\]
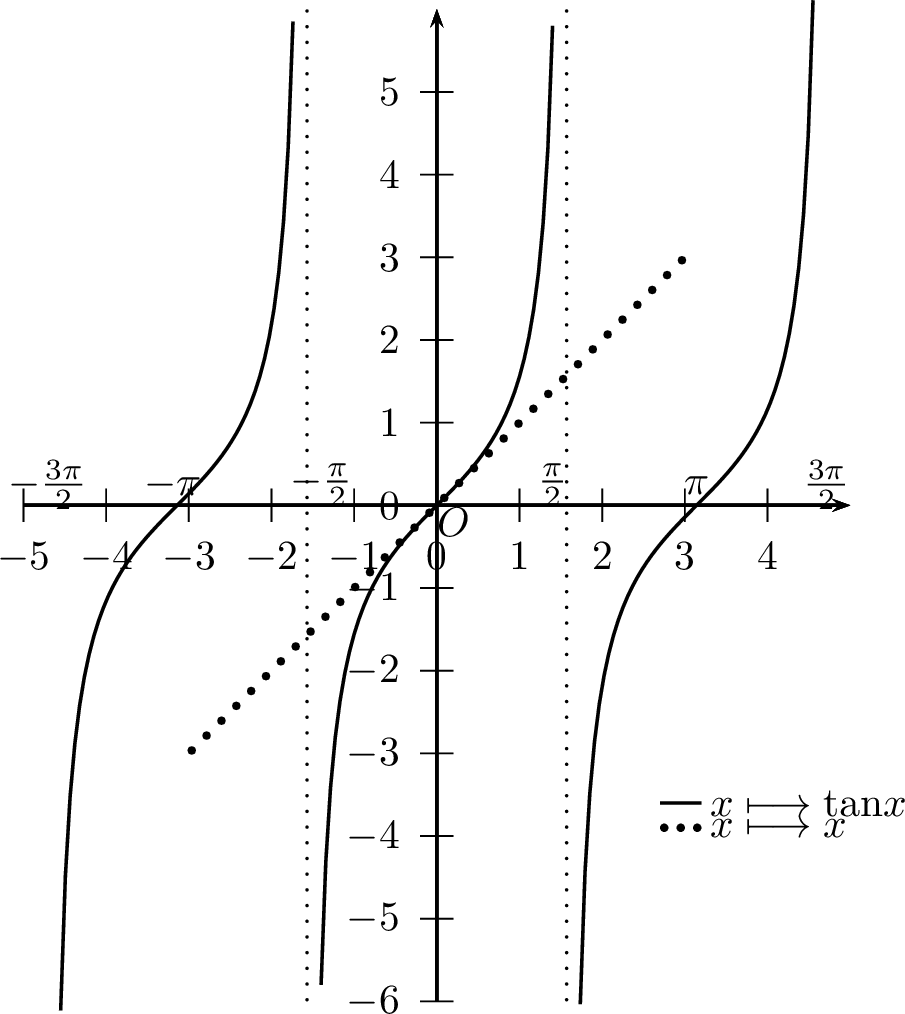
La fonction tangente, notée \(\tan\), et donnée par : \[\boxed{\forall x\in\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+ k\pi ~|~ k\in\mathbb{Z}\right\}, \quad \tan x = \dfrac{\sin x}{\cos x}}\] est :
définie sur \(\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+ k\pi ~|~ k\in\mathbb{Z}\right\}\).
à valeurs dans \(\mathbb{R}\).
impaire.
\(\pi\)-périodique.
continue \(\mathbb{R}\setminus\left\{\dfrac{\pi}{2} +k\pi ~|~ k\in\mathbb{Z}\right\}\).
dérivable sur \(\mathbb{R}\) et \[\boxed{\forall x\in\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+ k\pi ~|~ k\in\mathbb{Z}\right\}, \quad \tan' x=1+\tan^2 x=\dfrac{1}{\cos^2 x}}\]
declasse \(\mathcal{C}^{\infty}\) sur \(\mathbb{R}\setminus\left\{\dfrac{\pi}{2}+ k\pi ~|~ k\in\mathbb{Z}\right\}\).
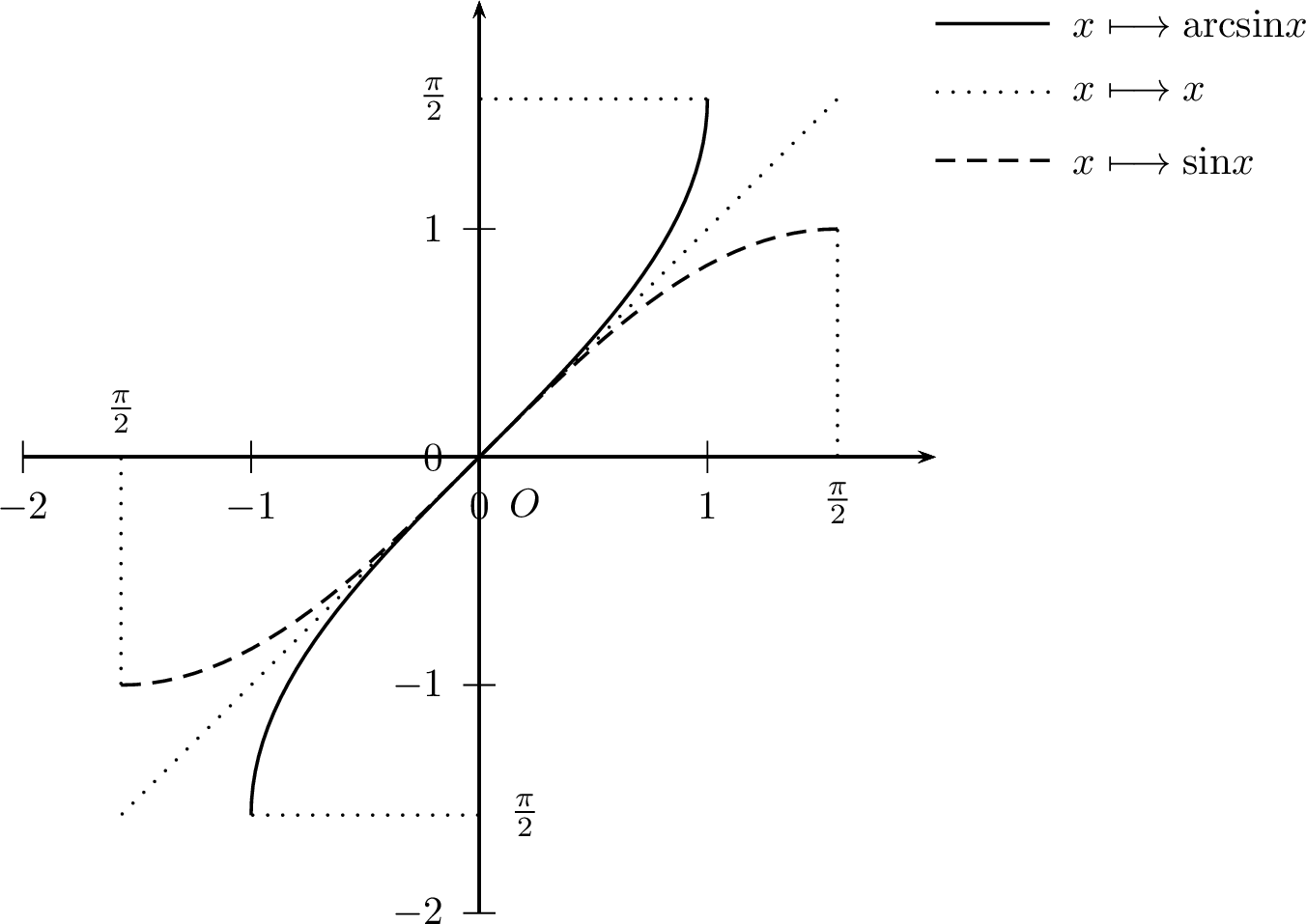
Fonction Arcsinus
est strictement croissante sur \(\left[-1,1\right]\).
est impaire.
est continue sur \(\left[-1,1\right]\).
est dérivable sur \(\left]-1,1\right[\) et \[\boxed{\forall y\in\left]-1,1\right[, \quad \operatorname{arcsin} ' y=\dfrac{1}{\sqrt{1-y^2}}}\]
réalise une bijection de \(\left[-1,1\right]\) dans \(\left[-\pi/2,\pi/2\right]\)
continue
strictement croissante.
Par application du
strictement monotone sur \(I\)
dérivable sur \(I\).
et vérifie \(\forall x\in I,\quad \sin'\left(x\right)=\cos x \neq 0\)
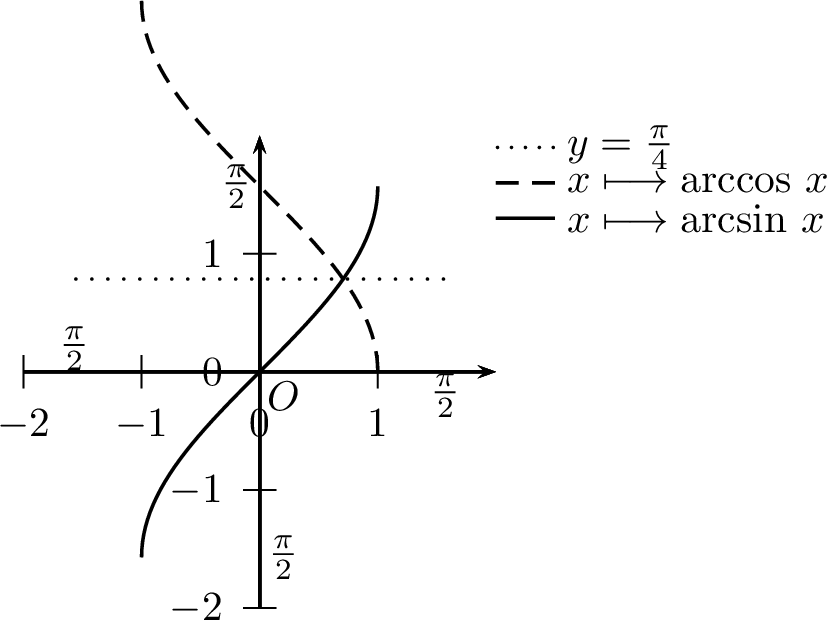
Fonction Arccosinus
\[\begin{aligned} \forall y\in\left[-1,1\right], & & \cos\left(\operatorname{arccos} y\right)=y\\ \forall x\in\left[0,\pi\right], & & \operatorname{arccos} \left(\cos x\right)=x \end{aligned}\]
De plus \(\operatorname{arccos}\) : \(\quad\)
est strictement décroissante sur \(\left[-1,1\right]\).
est continue sur \(\left[-1,1\right]\).
est dérivable sur \(\left]-1,1\right[\) et : \[\boxed{\forall y\in\left]-1,1\right[, \quad \operatorname{arccos} ' y=\dfrac{-1}{\sqrt{1-y^2}}}\]
est \(\mathcal{C}^{\infty}\) sur \(\left]-1,1\right[\).
réalise une bijection de \(\left[-1,1\right]\) dans \(\left[0,\pi\right]\)
continue.
strictement décroissante.
Par application du
strictement monotone sur \(I\)
dérivable sur \(I\).
et vérifie \(\forall x\in I,\quad \cos'\left(x\right)=-\sin x \neq 0\)
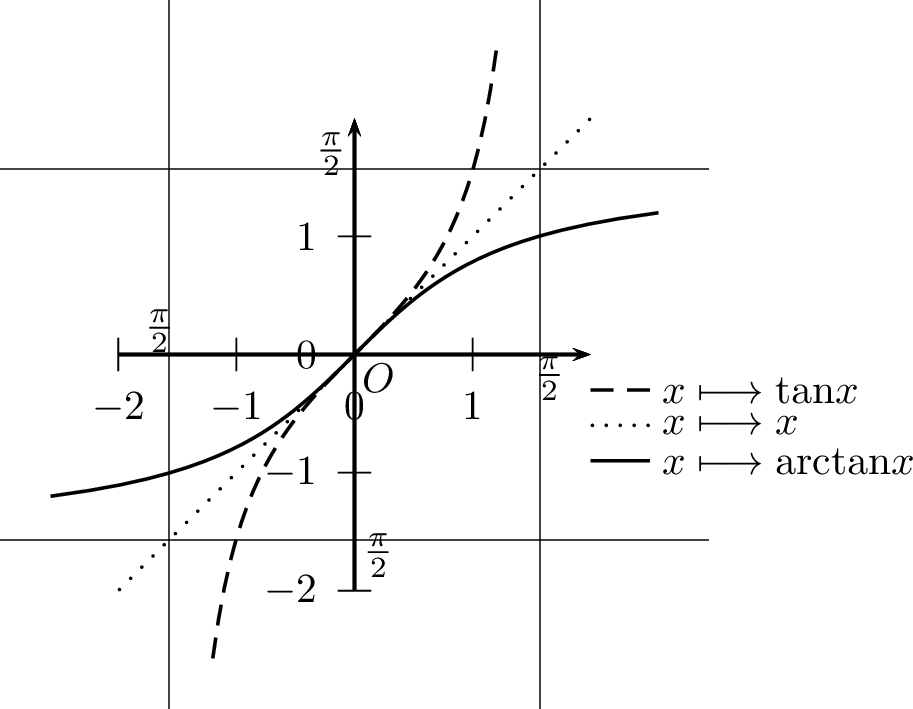
Fonction Arctangente
\[\begin{aligned} \forall y\in\mathbb{R}, & & \tan\left(\operatorname{arctan} y\right)=y\\ \forall x\in\left]-\dfrac{\pi}{2},\dfrac{\pi}{2}\right[, & & \operatorname{arctan} \left(\tan x\right)=x \end{aligned}\] La fonction \(\operatorname{arctan}\) \(\quad\)
est strictement croissante sur \(\mathbb{R}\).
est impaire.
est continue sur \(\mathbb{R}\).
est dérivable sur \(\mathbb{R}\) et : \[\boxed{\forall y\in\mathbb{R}, \quad \operatorname{arctan} ' y=\dfrac{1}{1+y^2}}\]
est \(\mathcal{C}^{\infty}\) sur \(\mathbb{R}\).
réalise une bijection de \(\mathbb{R}\) dans \(\left]-\pi/2,\pi/2\right[\).
strictement monotone sur \(I\)
dérivable sur \(I\).
et vérifie \(\forall x\in I,\quad \tan'\left(x\right)=\dfrac{1}{\cos^2 x} \neq 0\)
Fonctions hyperboliques
Définitions et premières propriétés
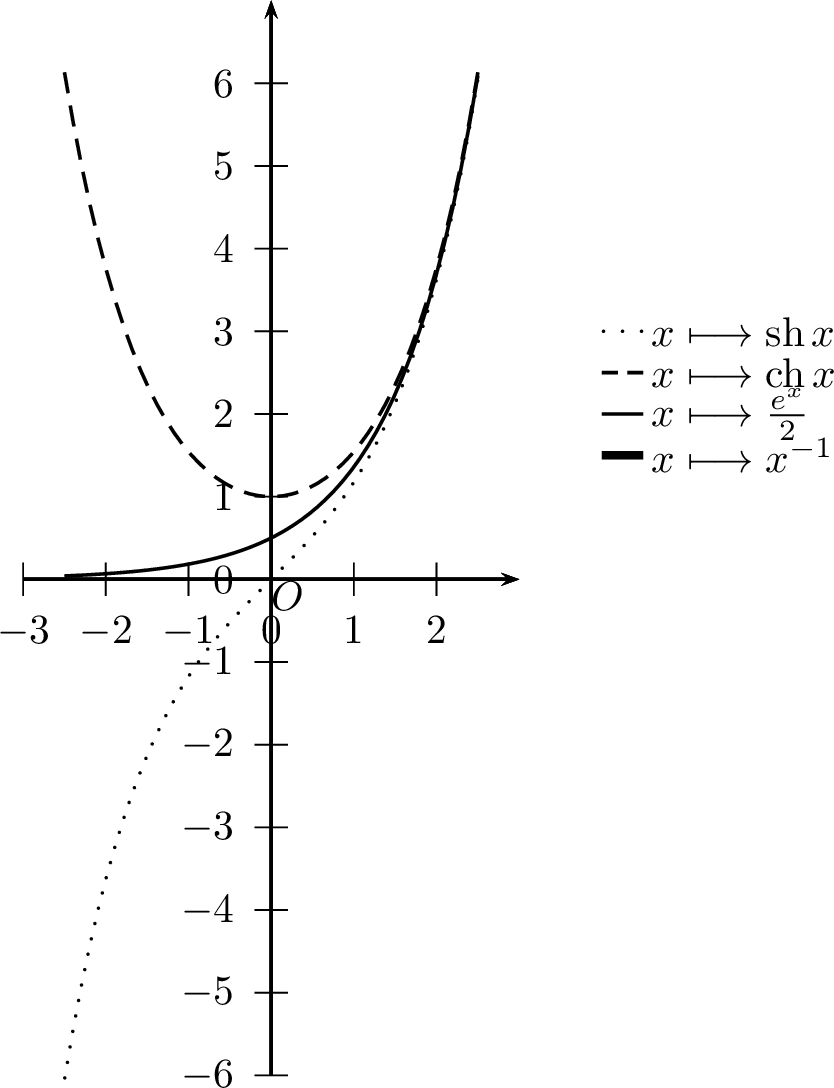
Sinus et Cosinus hyperboliques
\(\boxed{\mathop{\mathrm{ch}}x+\mathop{\mathrm{sh}}x=e^x}\)
\(\boxed{\mathop{\mathrm{ch}}x-\mathop{\mathrm{sh}}x=e^{-x}}\)
\(\boxed{\mathop{\mathrm{ch}}^2 x-\mathop{\mathrm{sh}}^2 x=1}\)
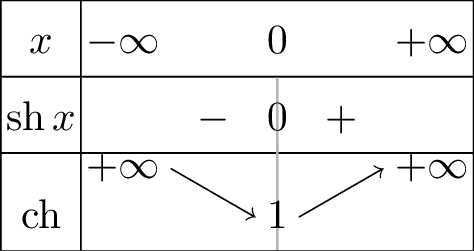
La fonction \(\mathop{\mathrm{sh}}\) est impaire, strictement croissante sur \(\mathbb{R}\), strictement négative sur \(\mathbb{R}_-^*\) et strictement positive sur \(\mathbb{R}_+^*\) et s’annule en \(0\).
La fonction \(\mathop{\mathrm{ch}}\) est paire, strictement positive sur \(\mathbb{R}\), strictement décroissante sur \(\mathbb{R}_-^*\) et strictement croissante sur \(\mathbb{R}_+^*\). De plus, \(\forall x\in \mathbb{R}, \quad \mathop{\mathrm{ch}}x \geqslant 1\).
Les fonctions \(\mathop{\mathrm{ch}}\) et \(\mathop{\mathrm{sh}}\) sont declasse \(\mathcal{C}^{\infty}\) sur \(\mathbb{R}\) comme combinaison linéaire de fonctions \(\mathcal{C}^{\infty}\) sur \(\mathbb{R}\). Appliquant les théorèmes de dérivation, on vérifie sans peine les formules annoncées pour leurs dérivées respectives.
\(\mathop{\mathrm{sh}}\) et \(\mathop{\mathrm{ch}}\) sont respectivement impaire et paire par construction.
\(\mathop{\mathrm{ch}}\) est une fonction strictement positive sur \(\mathbb{R}\) car la fonction exponentielle est strictement positive sur \(\mathbb{R}\). Par conséquent, \(\mathop{\mathrm{sh}}\) a une dérivée strictement positive sur \(\mathbb{R}\) et est strictement croissante sur \(\mathbb{R}\).
Par application des propriétés sur les limites d’après les limites de la fonction exponentielle à ses bornes, on vérifie sans peine les limites annoncées.
Évaluant \(\mathop{\mathrm{sh}}\) en \(0\), on vérifie immédiatement qu’elle s’annule en \(0\). Comme elle est strictement croissante et continue, on en déduit qu’elle est strictement négative sur \(\mathbb{R}_-^*\) et strictement positive sur \(\mathbb{R}_+^*\).
La fonction dérivée de \(\mathop{\mathrm{ch}}\) sur \(\mathbb{R}\) étant \(\mathop{\mathrm{sh}}\), on déduit de cette dernière propriété que \(\mathop{\mathrm{ch}}\) est strictement décroissante sur \(\mathbb{R}_-^*\) et strictement croissante sur \(\mathbb{R}_+^*\).
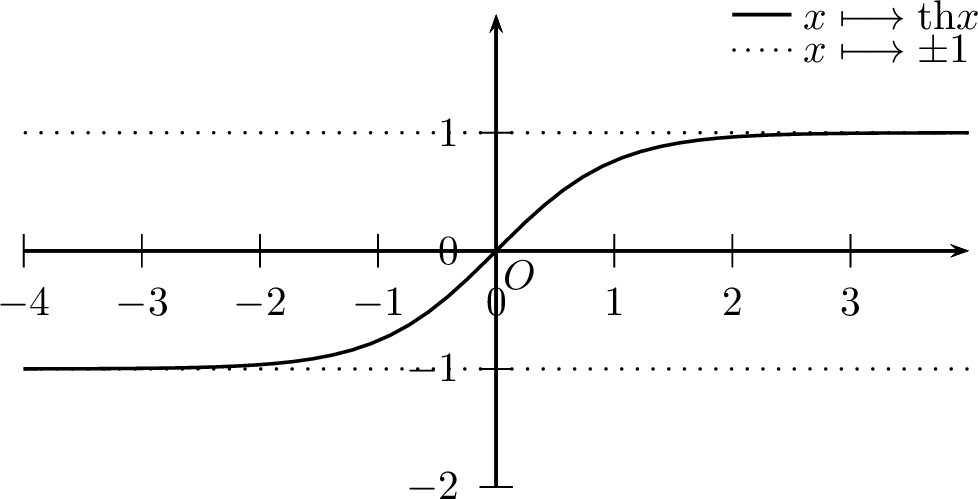
Tangente hyperbolique
Formulaire de trigonométrie hyperbolique
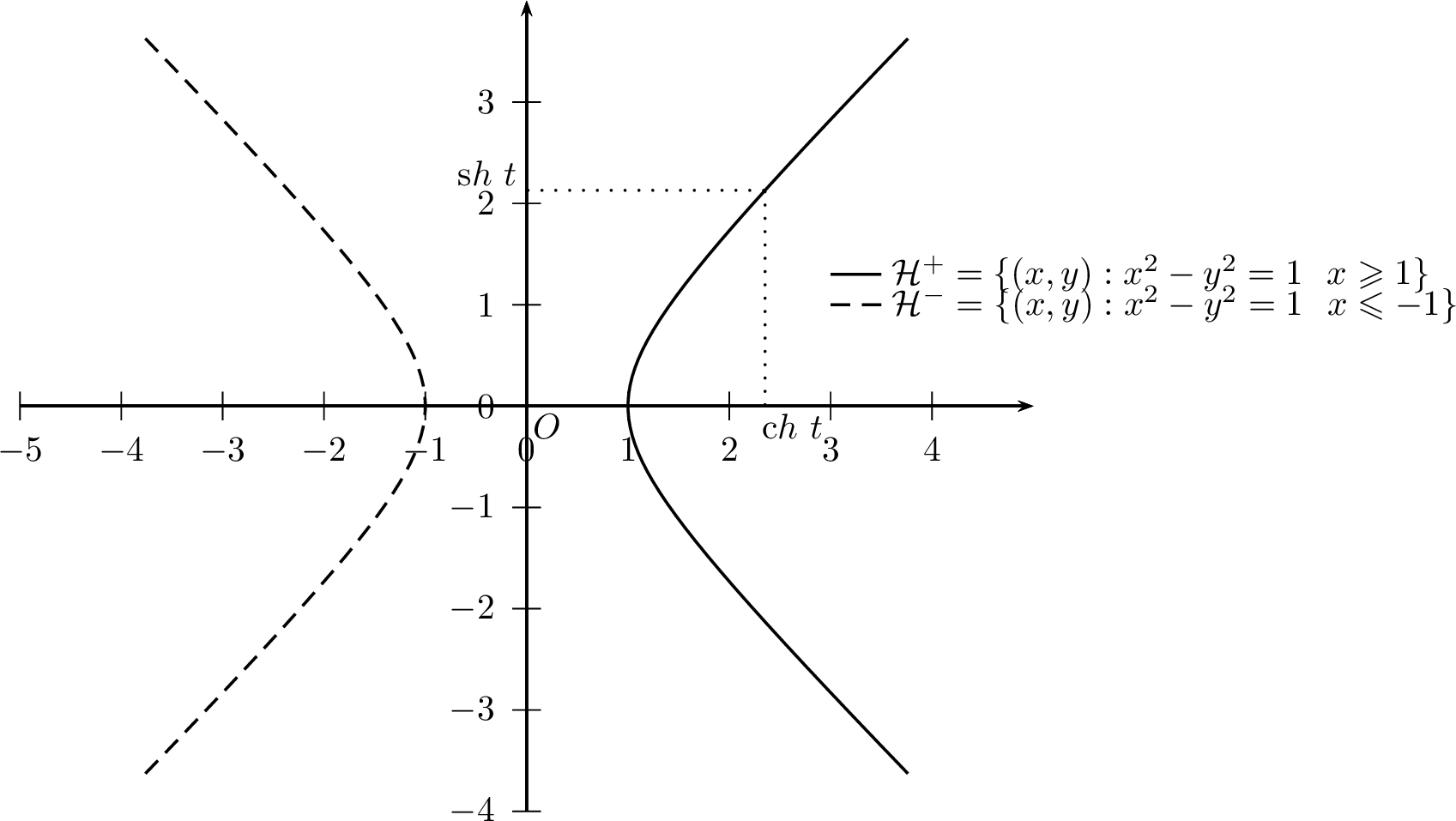
Tout comme les fonctions cosinus et sinus permettent de paramétrer le cercle unité, les fonctions \(\mathop{\mathrm{ch}}\) et \(\mathop{\mathrm{sh}}\) donnent une paramétrisation de l’hyperbole équilatère de sommets \(\left(1,0\right)\) et \(\left(-1,0\right)\). Le formulaire de trigonométrie hyperbolique ressemble fort au formulaire de trigonométrie classique. On le trouvera dans l’annexe [AnnexeE] paragraphe [Formulaire_Trigo_hyperbolique].
Donnons à titre d’exemples les formules d’addition.
Fonctions hyperboliques inverses
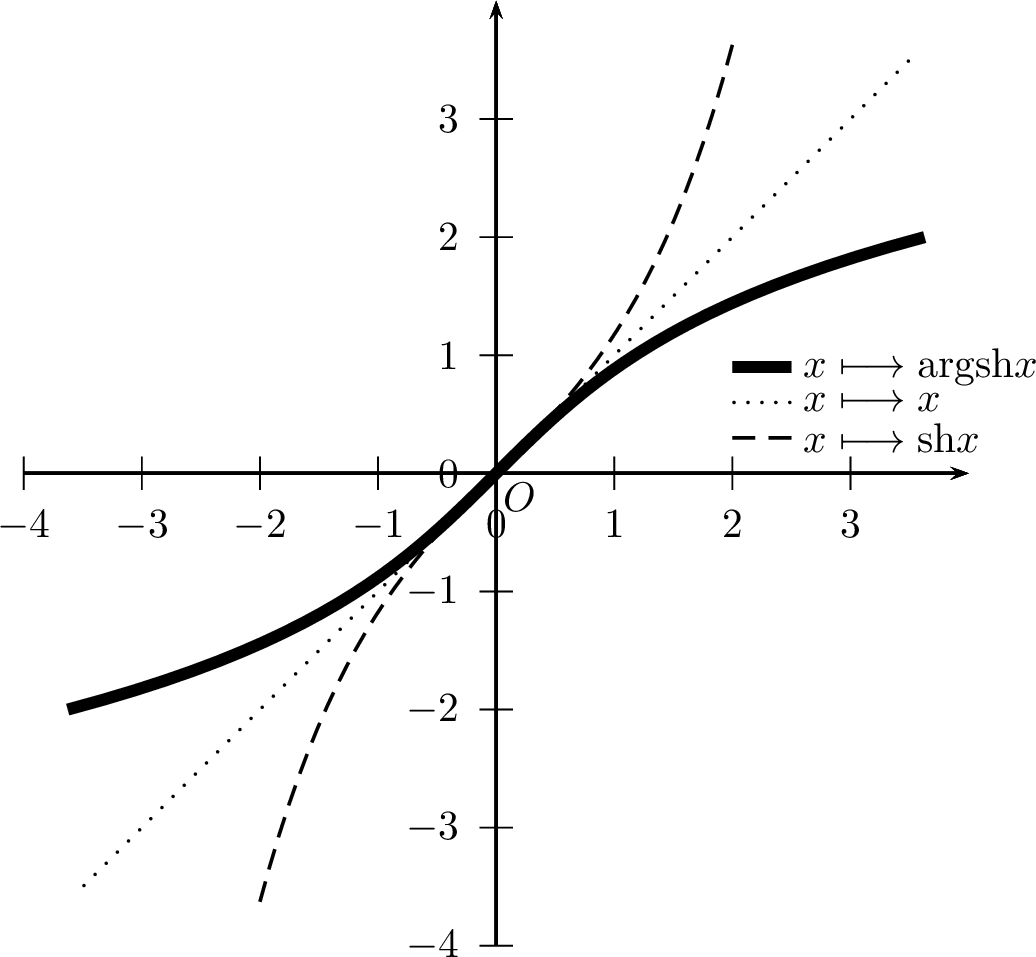
Fonction argument sinus hyperbolique \(\mathop{\mathrm{argsh}}\)
La
\[\begin{aligned} \forall y\in\mathbb{R}, & & \mathop{\mathrm{sh}}\left(\mathop{\mathrm{argsh}}y\right)=y\\ \forall x\in\mathbb{R}, & & \mathop{\mathrm{argsh}}\left(\mathop{\mathrm{sh}}x\right)=x\end{aligned}\] La fonction \(\mathop{\mathrm{argsh}}\)
est impaire.
est continue sur \(\mathbb{R}\).
est dérivable sur \(\mathbb{R}\) et \[\boxed{\forall y\in\mathbb{R}, \quad \mathop{\mathrm{argsh}}' y=\dfrac{1}{\sqrt{y^2+1}}}\]
est strictement croissante sur \(\mathbb{R}\).
réalise une bijection de \(\mathbb{R}\) dans \(\mathbb{R}\).
est strictement monotone
est dérivable
et vérifie : \(\forall x\in I,\quad \mathop{\mathrm{sh}}'\left(x\right)=\mathop{\mathrm{ch}}x \neq 0\)
Expression logarithmique :
On résout l’équation \(y = \dfrac{e^x - e^{-x}}{2}\) soit \(e^{2x} - 2ye^x - 1=0\). En posant \(T = e^x\), on résout \(T^2 - 2yT - 1 = 0\). On a deux racines \(T_1 = y + \sqrt{1+y^2}\) et \(T_2 = y - \sqrt{1+y^2}\) dont une seule est positive. D’où \(x = \ln T_1 = \ln \left( y + \sqrt{1+y^2} \right)\).
Donc \(\mathop{\mathrm{argsh}}y = \ln \left( y + \sqrt{1+y^2} \right)\). Vérification : Lorsqu’on dérive \(f(y) = \ln \left( y + \sqrt{1+y^2} \right)\) on obtient \(f'(y) = \dfrac {1+ {\scriptstyle 2y\over\scriptstyle 2\sqrt{1+y^2} }} {1 + \sqrt{1+y^2} } = \dfrac {{\scriptstyle\sqrt{1+y^2}\over\scriptstyle\sqrt{1+y^2}} +{\scriptstyle 2y\over\scriptstyle 2\sqrt{1+y^2}}} {1 + \sqrt{1+y^2}} = \dfrac{1} {\sqrt{1+y^2}}\). Comme \(f(0) = 0\), on a bien \(f(y) = \mathop{\mathrm{argsh}}y\) sur l’intervalle \(\mathbb{R}\).
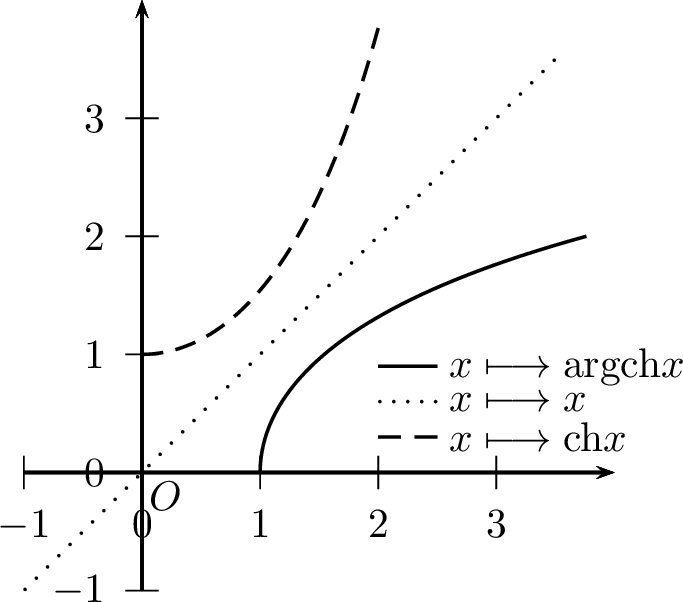
Fonction Argument cosinus hyperbolique \(\mathop{\mathrm{argch}}\)
La
est continue sur \(\left[1,+\infty\right[\).
est dérivable sur \(\left]1,+\infty\right[\) et : \[\boxed{\forall y\in\left]1,+\infty\right[, \quad \mathop{\mathrm{argch}}' y=\dfrac{1}{\sqrt{y^2-1}}}\]
est strictement croissante sur \(\left[1,+\infty\right[\).
réalise une bijection de \(\left]1,+\infty\right[\) dans \(\mathbb{R}\).
continue.
strictement croissante.
Par application du
strictement monotone sur \(I\)
dérivable sur \(I\).
et vérifie : \(\forall x\in I,\quad \mathop{\mathrm{ch}}'\left(x\right)=\mathop{\mathrm{sh}}x \neq 0\)
Expression logarithmique :
Soit \(x\geqslant0\). On résout l’équation \(y = \dfrac{e^x + e^{-x}}{2}\) pour \(y\geqslant1\), soit \(e^{2x} - 2ye^x + 1=0\). En posant \(T = e^x\), on résout \(T^2 - 2yT + 1 = 0\). On a deux racines \(T_1 = y + \sqrt{y^2-1}\) et \(T_2 = y - \sqrt{y^2-1}\) dont une seule est supérieure ou égale à \(1\) (leur produit égale \(1\)). D’où \(x = \ln T_1 = \ln \left( y + \sqrt{y^2-1} \right)\).
Donc \(\mathop{\mathrm{argch}}y = \ln \left( y + \sqrt{y^2-1} \right)\). Vérification : Lorsqu’on dérive pour \(y>1\), \(f(y) = \ln \left( y + \sqrt{y^2-1} \right)\) on obtient \(f'(y) = \dfrac{1+{\scriptstyle 2y\over\scriptstyle 2\sqrt{y^2-1}}}{1 + \sqrt{y^2-1}} = \dfrac{{\scriptstyle\sqrt{y^2-1}\over\scriptstyle\sqrt{y^2-1}}+{\scriptstyle 2y\over\scriptstyle 2\sqrt{y^2-1}}}{1 + \sqrt{y^2-1}} = \dfrac{1}{\sqrt{y^2-1}}\). Comme \(f(1) = 0\), on a bien \(f(y) = \mathop{\mathrm{argch}}y\) sur l’intervalle \(\mathbb{R}_+\).
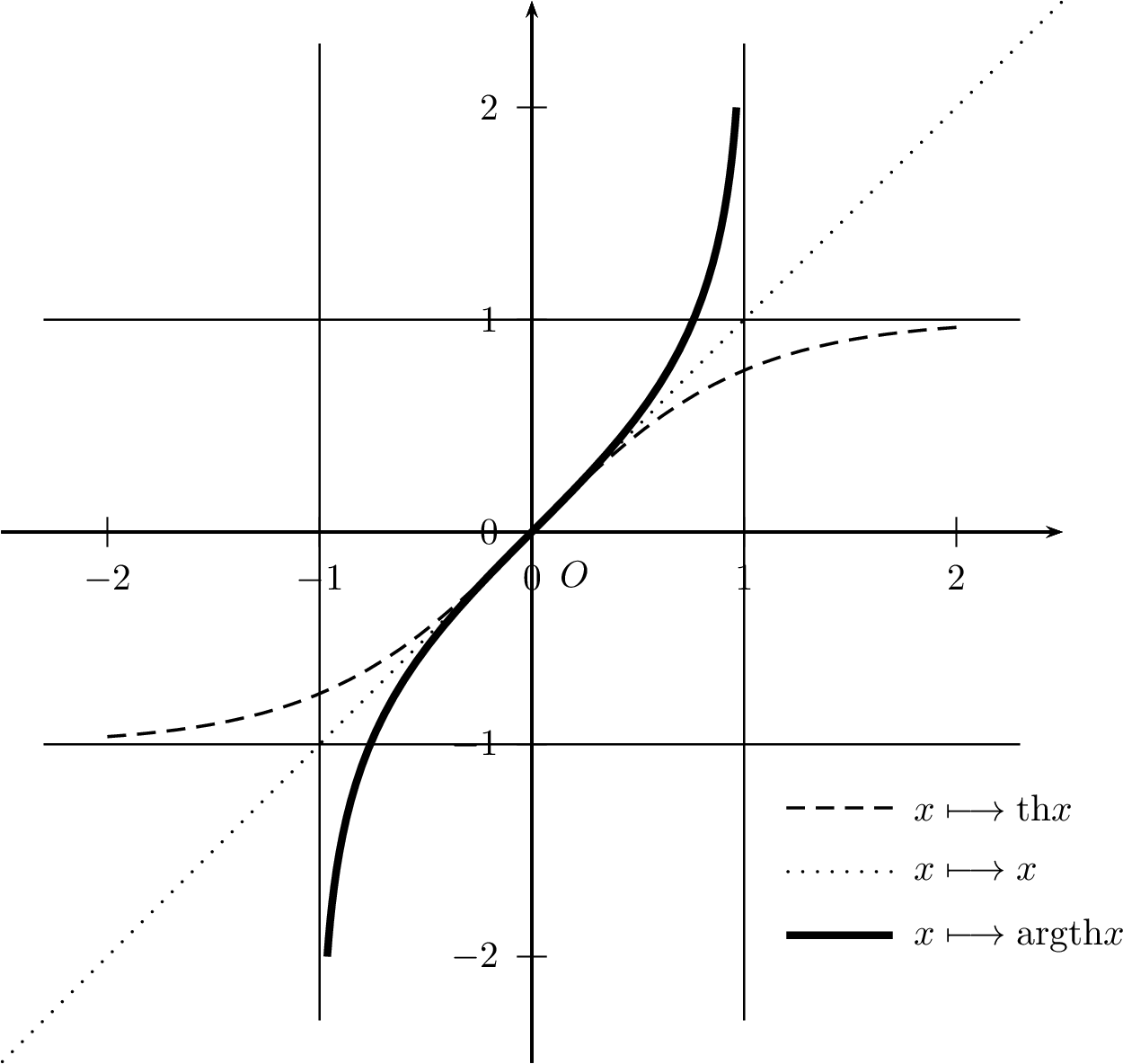
Fonction Argument tangente hyperbolique \(\mathop{\mathrm{argth}}\)
La fonction
\[\begin{aligned} \forall y\in\left]-1,1\right[, & & \operatorname{th} \left(\mathop{\mathrm{argth}}y\right)=y\\ \forall x\in\mathbb{R}, & & \mathop{\mathrm{argth}}\left(\operatorname{th} x\right)=x\end{aligned}\]
La fonction \(\mathop{\mathrm{argth}}\)
est impaire.
est strictement croissante sur \(\left]-1,1\right[\).
est continue sur \(\left]-1,1\right[\).
est dérivable sur \(\left]-1,1\right[\) et \[\boxed{\forall y\in\left]-1,1\right[, \quad \mathop{\mathrm{argth}}' y=\dfrac{1}{1-y^2}}\]
réalise une bijection de \(\left]-1,1\right[\) dans \(\mathbb{R}\).
est \(\mathcal{C}^{\infty}\) sur \(\left]-1,1\right[\).
est strictement monotone sur \(I\)
est dérivable sur \(I\).
et vérifie \(\forall x\in I,\quad \operatorname{th} '\left(x\right)=\dfrac{1}{\mathop{\mathrm{ch}}^2 x} \neq 0\)
Expression logarithmique :
On résout l’équation \(y = \dfrac{e^x - e^{-x}}{e^x + e^{-x}} = \dfrac{e^{2x}-1}{e^{2x}+1}\) pour \(\vert y\vert <1\), soit \(e^{2x}(1-y) = 1+y\), soit \(e^{2x} = \dfrac{1+y}{1-y}\) et \(x = \dfrac12\,\ln\left( \dfrac{1+y}{1-y}\right)\).
Donc \(\mathop{\mathrm{argth}}y = \dfrac12\,\ln\left( \dfrac{1+y}{1-y}\right)\). Vérification : Lorsqu’on dérive pour \(y>1\), \(f(y) = \dfrac12\,\ln\left( \dfrac{1+y}{1-y}\right)\) on obtient bien \(f'(y) = \dfrac{1}{1 -y^2}\). Comme \(f(0) = 0\), on a bien \(f(y) = \mathop{\mathrm{argth}}y\) sur l’intervalle \(]-1,1[\).
Deux exemples
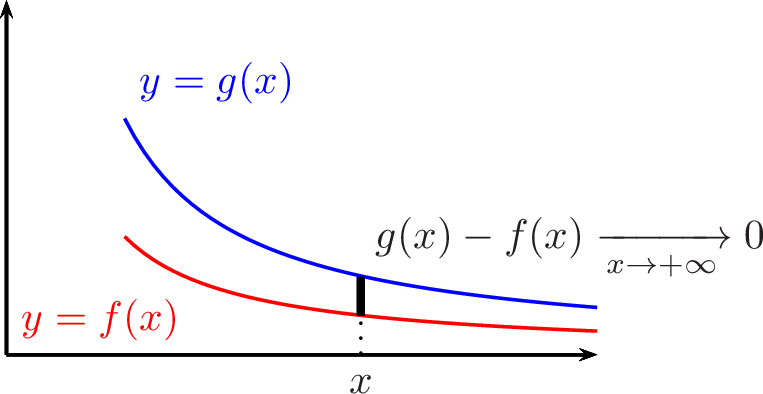
Si \(f(x) \xrightarrow[ x\rightarrow +\infty ]{ } l \in \mathbb{R}\), la droite horizontale \(y=l\) est asymptote. On lit sur le tableau de variations la position de la courbe par rapport à l’asymptote.
Si \(f(x) \xrightarrow[ x\rightarrow +\infty ]{ } \infty\), on calcul la limite de \(f(x)/x\) en \(+\infty\).
Si cette limite existe et est égal à un réel \(a\neq 0\), on calcule \(f(x)-ax\) et on cherche la limite de \(f(x)-ax\) en \(+\infty\). Si \(f(x)-ax \rightarrow b \in \mathbb{R}\), la droite \(y=ax+b\) est asymptote. On détermine la position de la courbe par rapport à l’asymptote en étudiant le signe de \(f(x)-[ax+b]\) au voisinage de \(+\infty\).
Si \(\dfrac{f(x)}{x}\rightarrow \infty\), on dit qu’on a une branche parabolique de direction \((0y)\). Si \(\dfrac{f(x)}{x}\rightarrow 0\), une branche parabolique de direction \((0x)\).
Si \(f(x)/x^2\) admet une limite finie \(a\) non nulle et que ce n’est pas le cas de \(f\left(x\right)/x\), on peut rechercher des parabolesasymptotes .
Trouver le domaine de définition.
Calculer la dérivée (factoriser) et étudier son signe.
Tableau de variations. On précise les valeurs exactes remarquables, les limites et les prolongements éventuels (on étudie alors la dérivabilité de la fonction prolongée).
Recherche d’éventuellesasymptotes .
Tracé approximatif de la courbe \(y=f(x)\) : on représente lesasymptotes éventuelles, les tangentes horizontales
Comme : \[f(x) = x^{x+1}=e^{\left(x+1\right)\ln x}.\] \(f\) est définie sur \(\mathbb{R}_+^*\).
Soit \(x\in\mathbb{R}_+^*\). On a : \(f'\left(x\right) = \dfrac{x\ln x +{x+1}}{x} x^{x+1}\) donc \(f\) est du signe de \(x\ln x +{x+1}\). Introduisons la fonction : \(g: \left\{ \begin{array}{ccl} \mathbb{R}_+^* & \longrightarrow & \mathbb{R} \\ x & \longmapsto & x\ln x +{x+1} \end{array} \right.\). Pour tout \(x\in\mathbb{R}_+^*\) : \(g'\left(x\right)=\ln x+2\). On en déduit les variations de \(g\) et le signe de \(f'\).
Remarquons que \(g\left(e^{-2}\right) >0\) et en utilisant les limites usuelles, on obtient : \(g\left(x\right)\xrightarrow[x\rightarrow 0^+]{}1\).
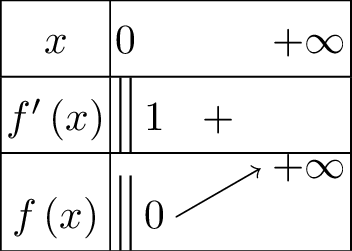
Le tableau de variation de \(f\) est donc :
les limites étant obtenues en utilisant les limites usuelles et par opération sur les limites.
Le graphe de \(f\) admet une branche infinie quand \(x\rightarrow +\infty\). Si \(x\in\mathbb{R}_+^*\) : \[\dfrac{x^{x+1}}{x} = x^x \xrightarrow[x\rightarrow +\infty]{}+\infty.\] Le graphe de \(f\) n’admet donc pas d’asymptote quand \(x\rightarrow +\infty\). On a affaire à une branche parabolique de direction \(Oy\).
On en déduit le graphe de \(f\) :
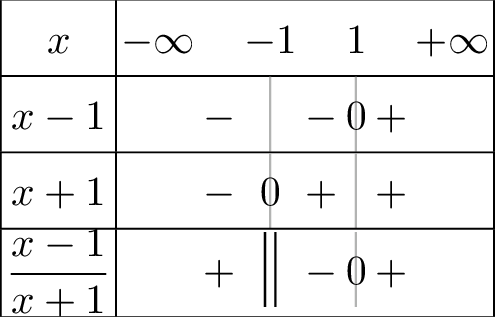
Nous déduisons du tableau de signe
que \(f\) est définie sur \(I=\left]-\infty,-1\right[\cup \left[1,+\infty\right[\).
\(f\) est dérivable sur \(\left]-\infty,-1\right[\cup \left]1,+\infty\right[\) car la fonction racine carrée est dérivable sur \(\mathbb{R}_+^*\). Soit \(x\) un élément de cet ensemble. On trouve : \[f'\left(x\right)=\dfrac{x^2+x-1}{\sqrt{\dfrac{x-1}{x+1}}\left(x+1\right)^2}.\] \(f'\) est donc du signe de \(x^2+x-1\). Les racines de ce trinômes sont \(\alpha=\left(-1+\sqrt 5\right)/2\) et \(\beta=\left(-1-\sqrt 5\right)/2\). Seul \(\alpha\) est dans le domaine de définition de \(f\). Pour les limites, on remarque que : \[f\left(x\right)=x\sqrt{\dfrac{1-{\scriptstyle 1\over\scriptstyle x}}{1+{\scriptstyle 1\over\scriptstyle x}}}\] et donc \(\displaystyle{\lim_{x \rightarrow -\infty}f\left(x\right)}=-\infty\), \(\displaystyle{\lim_{x \rightarrow +\infty}f\left(x\right)}=+\infty\). Par limites usuelles, il est clair que \(\displaystyle{\lim_{x \rightarrow -1^-}f\left(x\right)}=-\infty\). On en déduit de la tableau de variation suivant :
Le graphe de \(f\) admet une branche infinie quand \(x\rightarrow \pm\infty\) et quand \(x\rightarrow -1^-\).
\[\dfrac{f\left(x\right)}{x}=\sqrt{\dfrac{x-1}{x+1}}=\sqrt{\dfrac{1-{\scriptstyle 1\over\scriptstyle x}}{1+{\scriptstyle 1 \over\scriptstyle x}}} \xrightarrow[x\rightarrow \pm \infty]{} 1\] et par multiplication par les quantités conjuguées, \[f\left(x\right)-x = x\left(\sqrt{\dfrac{x-1}{x+1}} -1\right) =x\dfrac{\dfrac{x-1}{x+1}-1 }{ \sqrt{\dfrac{x-1}{x+1}} +1 }=\dfrac{\dfrac{-2x}{x+1} }{ \sqrt{\dfrac{x-1}{x+1}} +1 }=\dfrac{\dfrac{-2}{1+{\scriptstyle 1\over\scriptstyle x}} }{ \sqrt{\dfrac{1-{\scriptstyle 1\over\scriptstyle x}}{1+{\scriptstyle 1\over\scriptstyle x}}} +1 }\xrightarrow[x\rightarrow \pm \infty]{} -1\] La droite d’équation \(\boxed{y=x-1}\) est donc asymptote à la courbe au voisinage de \(+\infty\) et \(-\infty\).
On a une asymptote verticale au voisinage de \(-1\) d’équation \(x=-1\).
On en déduit le graphe de \(f\) :
Fonction exponentielle complexe
Soit \(I\) un intervalle de \(\mathbb{R}\). On s’intéresse ici à une fonction \(f\) définie sur \(I\) et à valeurs complexes \(f:I\in \mathbb{C}\). Pour tout \(t\in I\), une telle fonction s’écrit sous la forme : \(f\left(t\right)=x\left(t\right)+i y\left(t\right)\). avec \(x,y: I\rightarrow \mathbb{R}\). Les fonctions \(x\) et \(y\) sont respectivement la partie réelle et la partie imaginaire de \(f\).
Soit \(t_0\in I\). On dit que \(f\) est dérivable en \(t_0\) si et seulement si \(x\) et \(y\) le sont. Dans ce cas, on définit \(f'\left(t_0\right)\) par : \[f'\left(t_0\right)=x'\left(t_0\right)+iy'\left(t_0\right).\]
En résumé
Il est opportun de lire les paragraphes [AnnexeC_Inegalites] et [AnnexeC_derivees] de l’annexe [AnnexeC] qui contiennent des méthodes pour construire des inégalités et dans lesquels sont promulgués quelques conseils pour le calcul des dérivées. Au terme de ce chapitre, le formulaire sur les dérivées des fonctions usuelles [Formulaire_Derivees_usuelles] et celui sur les limites usuelles [Formulaire_Limites_usuelles] devront être parfaitement connus. Vous devrez par ailleurs être totalement familier avec ces nouvelles fonctions que vous serez amené à manipuler quotidiennement en sup et en spé.
Il conviendra de retenir parfaitement les graphes et l’expression des dérivées des fonctions introduites dans ce chapitre.
Bibliographie
Barre utilisateur
[ID: 33] [Date de publication: 15 mars 2021 16:48] [Catégorie(s): Le cours de SUP ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]Documents à télécharger
L'article complet