La vieille géométrie remonte selon les auteurs aux alentours de -3000, et les "Éléments" d’Euclide dateraient d’environ 300 avant JC. Le fameux théorème de Pythagore remonterait au 6ème siècle avant JC et aurait entraîné divers problèmes philosophiques liés à l’irrationalité (l’incommensurabilité). Il faudra par contre attendre le 19ème siècle pour que le polémique postulat des parallèles soit remis en cause. Précisément, ce postulat avait été remis en cause nombre de fois au sens où les gens avaient essayé de le démontrer à partir des autres axiomes, afin d’en faire un théorème plutôt qu’un axiome; les mathématiciens ne s’étaient pas trompé en sentant que ce postulat était plus complexe, moins naturel que les autres axiomes: on peut (comme pour l’axiome du choix en théorie des ensembles) dire des choses intéressantes en le supprimant et en choisissant un autre jeu d’axiomes à la place. De manière amusante, la théorie des ensembles permet de construire des modèles de chacune de ces géométries, montrant ainsi que toutes ont leur consistance (si ZF est consitant). Naissent alors des géométries non-euclidiennes:
plus de parallèles du tout: la géométrie elliptique (penser aux espaces projectifs, qui sont bien construits à partir de la théorie des ensembles et sont donc bien des modèles de géométrie elliptique, où il n’y a pas de parallèle)1;
plein de parallèles différentes (au sens: une droite est parallèle à une autre si elles ne se touchent jamais) à une droite donnée passant par un point donné: la géométrique dite hyperbolique (penser à la restriction d’un espace euclidien à une boule - là aussi, la construction d’espaces euclidiens étant possibles en théorie des ensembles, on voit bien ainsi apparaître un modèle de géométrie où on peut trouver plein de "parallèles" - c’est-à-dire ici des segments maximaux de la boule à une droite donnée passant par un point donné).
Ces géométries moins intuitives (et d’autres qu’on ne citera pas ici, par exemple les variétés de Calabi-Yau en théorie des cordes) auront leur heure de gloire avec l’avènement de la relativité en physique, qui va très au-delà de cet ouvrage.
Cette partie concerne tant la géométrie affine que la géométrie projective et la théorie des groupes ou des polygones et polyèdres réguliers. En fait la géométrie projective et la géométrie affine sont souvent liées; et certains théorèmes de géométrie affine seront prouvés par la géométrie projective (et réciproquement). La première section "étude de courbes" ([etc1]), toutefois, est résolument affine. Les deux sections suivantes feront un lien avec la géométrie projective: dualité ([etc2]), géométries du plan et du plan projectif ([etc3]). On aura ensuite des liens avec la théorie des groupes: groupes orthogonaux et polygones et polyèdres réguliers ([etc4]), la célèbre droite de Simson (liée aux polynômes symétriques) et le cercle des neuf points ([etc5],[etc6]).
Etude de courbes
(Position d’une courbe par rapport à sa direction).
Etant donné \(\gamma\) un arc suffisamment dérivable de \([0,a]\) dans \(\mathbb{R}^d\), on considère (si elles existent) ses premières dérivées non nulles \(d1=\frac{d^m\gamma}{dx^m}\) et \(d2=\frac{d^n\gamma}{dx^n}\) en \(t\in [0,a]\) telles que \(d1\) et \(d2\) ne soient pas colinéaires2.
On dit que:
\(\frac{d\gamma}{dt}\) est appelé vitesse de \(\gamma\) en \(t\). On dit que l’arc est une abscisse ou abscisse curviligne si la vitesse a une norme constante égale à \(1\).
la droite passant par \(\gamma(t)\) et de direction \(d1\) est appelé direction de \(\gamma\) en \(t\).
\(t\), ou \(\gamma(t)\) s’il n’existe pas \(u\neq t\) tel que \(\gamma(t)=\gamma(u)\), est un point d’inflexion si \(m\) et \(n\) sont impairs (la courbe change alors en \(t\) de côté par rapport à sa direction en \(t\)).
\(t\) (ou \(\gamma(t)\)…) est un point de rebroussement de première espèce si \(m\) est pair et \(n\) est impair (la courbe "rebrousse chemin" et change alors en \(t\) de côté par rapport à sa direction en \(t\)).
\(t\) (ou \(\gamma(t)\)…) est un point de rebroussement de seconde espèce si \(m\) et \(n\) sont pairs (la courbe "rebrousse chemin" et ne change alors pas en \(t\) de côté par rapport à sa direction en \(t\)).
On parle de cas général si \(m\) est impair et \(n\) est pair; la courbe ne change alors pas en \(t\) de côté par rapport à sa direction en \(t\).
(Trièdre de Frenet).
On appelle trièdre de Frenet en \(t\) (avec les notations ci-dessus) de l’arc au moins \(C^2\)\(\gamma\), lorsque \(\gamma\) est une abscisse curviligne et lorsque les quantités qui suivent sont bien définies, le trièdre \((i,j,k)\) défini par \(i=\gamma'(t)\), \(j=\frac{1}{{\parallel}\frac{di}{dt}{\parallel}}\frac{di}{dt}\), \(k\) le produit vectoriel de \(i\) et \(j\). \({\parallel}\frac{di}{dt}{\parallel}\) est appelé courbure en \(t\). Son inverse \(1/{\parallel}\frac{di}{dt}{\parallel}\) est appelé rayon de courbure en \(t\). La torsion est \({\parallel}\frac{dk}{dt}{\parallel}\).
La droite passant par \(t\) et de direction \(i\) est appelée tangente en \(t\) (ou \(\gamma(t)\) lorsque cela ne prête pas à confusion).
Rappelons que la longueur d’un arc est l’intégrale de la norme de sa vitesse. Si la torsion est toujours nulle, la courbe est entièrement contenue dans un plan.
Si un arc a une vitesse toujours non nulle, on peut le reparamétrer en une abscisse curviligne. Il suffit en effet d’étudier \(\gamma\circ\varphi^{-1}\), avec \(\varphi(s)=\int_{s_0}^s {\parallel}\gamma'(s){\parallel}\,ds\).
La dualité
\(\boxcircle\) Quelques rappels d’algèbre linéaire
On considère un espace vectoriel \(E\) de dimension finie. On note, classiquement, \(E^*\) son dual (i.e. l’espace vectoriel des formes linéaires continues sur \(E\), c’est-à-dire, puisque \(E\) est de dimension finie, l’espace vectoriel des formes linéaires sur \(E\)).
Etant donné \(F\) un sous-espace vectoriel de \(E\), on note \(F'\) l’ensemble des formes linéaires nulles sur tout \(F\). Il est clair que \(F'\) un sous-espace vectoriel de \(E^*\) (voir la partie sur l’algèbre linéaire). On a \(dim\ F+dim\ F'=dim\ E\), et \(dim\ E^*=dim\ E\).
Rappelons que \(F \subset G\) dans \(E\) équivaut à \(G' \subset F'\) dans \(E^*\).
\(\boxcircle\) Le lien avec la géométrie projective
Notons maintenant bien ce qu’il se passe, lorsque l’on identifie \(E\) à \(E^*\):
On suppose que \(E\) est de dimension \(n\), et on note \(\pi_E\) la surjection canonique de \(E\) dans \(P(E)\).
Primal
Dual
dans \(E\)
dans \(P(E)\)
dans \(E^*\)
dans \(P(E^*)\)
\(dim\ E=n\)
\(dim\ P(E)=n-1\)
\(dim\ E^*=n\)
\(dim\ P(E^*)=n-1\)
\(F\subset E\)
\(\pi_E(F)\)
\(F'\)
\(\pi_{E^*}(F')\)
\(dim\ F=f\)
\(dim\ \pi_E(F)=f-1\)
\(dim\ F'=n-f\)
\(dim\ \pi_{E^*}(F')=n-f-1\)
\(D=\)
\(\pi_E(D)=\)
hyperplan
hyperplan
droite
point
(vectoriel)
(projectif)
\(G=\)
\(\pi_E(G)=\)
\(G'=\)
point
hyperplan
hyperplan
droite
(vectoriel)
(projectif)
(\(\pi_E\) est la projection canonique de \(E\) sur son projectif)
On peut aller plus loin, en traduisant cette fois-ci les relations d’inclusion et d’intersection. On note par la suite par des lettres les éléments de \(P(E)\), et par les mêmes lettres munies d’un \('\) leurs images dans \(P(E^*)\).
dans \(P(E)\)
dans \(P(E^*)\)
\(A \subset B\)
\(B'\subset A'\)
\(A \in B\)
\(B' \in A'\)
On peut ensuite spécialiser à la dimension \(2\): les lettres majuscules désignent des droites, les lettres minuscules des points; la même lettre désigne un élément et son dual; on ne fait que passer de minuscule à majuscule, et réciproquement.
dans \(P(E)\) (\(dim(E)=2\))
dans \(P(E^*)\)
\(a\) (un point)
\(A\) une droite
\(a=B \cap C\)
\(A=(bc)\)
\(A,B,C\) concourantes
\(a,b,c\) alignés
Triangle de côtés
Triangle de sommets
\(A\), \(B\) et \(C\)
\(a\), \(b\) et \(c\)
Tout cela se passe en projectif. En effet, en projectif, il est vrai que deux droites se croisent toujours en un point (dual du fait que par deux points passent toujours une droite), ce qui ne serait pas vrai en géométrie euclidienne standard!
Apllication On verra une application fort sympathique avec le théorème de Desargues [desar] (version géométrie projective).
Géométrie dans le plan et dans le plan projectif
Théorème de Pappus en géométrie affine
(Théorème de Pappus).
Soient \(D\) et \(D'\) deux droites du plan, distinctes.
Soient \(A\), \(B\) et \(C\) trois points de \(D\), et \(A'\), \(B'\) et \(C'\) trois points de \(D'\).
Si \(AB'\) est parallèle à \(BA'\),
et si \(CB'\) est parallèle à \(BC'\),
alors \(AC'\) est parallèle à \(CA'\),
\(\bullet\)Supposons tout d’abord que \(D\) et \(D'\) ne soient pas parallèles. Alors on considère \(O\) leur point d’intersection.
\(\bullet\)On oriente les deux droites \(D\) et \(D'\), et on constate que \(\frac{\overline{OB}}{\overline{OA}}=\frac{\overline{OA'}}{\overline{OB'}}\) et que \(\frac{\overline{OC}}{\overline{OB}}=\frac{\overline{OB'}}{\overline{OC'}}\) (par la réciproque du théorème de Thalès).
\(\bullet\)On en déduit que \(\frac{\overline{OA}}{\overline{OC}}=\frac{\overline{OC'}}{\overline{OA'}}\), ce qui par Thalès nous donne bien le résultat souhaité.
Notez qu’il est possible de raisonner sur des homothéties pour se débarasser des cas particuliers OC=0, etc. Il suffit de remplacer <<\(\frac{\overline{OB}}{\overline{OA}}=\frac{\overline{OA'}}{\overline{OB'}}\)>> par << il existe une homothétie \(h\) centrée sur \(O\) telle que \(h(A)=B\) et \(h(B')=A'\)>>.
\(\bullet\)Le cas \(D\) et \(D'\) parallèles n’est pas plus difficile, on utilise des translations pour exprimer les parallélismes...
Théorème de Desargues
On verra le théorème de Desargues sous deux formes, en géométrie affine et en version projective, la version projective fournissant une jolie démonstration de la réciproque. La réciproque étant valable aussi dans l’affine, on a ainsi une application de la géométrie projective en géométrie affine!
\(\boxcircle\) En géométrie affine
(Théorème de Desargues).
On se donne \(ABC\) et \(A'B'C'\) deux triangles sans sommet commun et à côtés respectivement parallèles 3. Alors \(AA'\), \(BB'\) et \(CC'\) sont concourantes ou parallèles.
\(\bullet\)Premier cas: \(AA'\) et \(BB'\) ne sont pas parallèles.
Alors elles se coupent en un point, disons \(O\).
\[\frac{\overline{OA'}}{\overline{OA}}=\frac{\overline{OB'}}{\overline{OB}}\] On considère alors le point \(M\) de \(OC\) tel que \[\frac{\overline{OA'}}{\overline{OA}}=\frac{\overline{OM}}{\overline{OC}}\] Par la réciproque du théorème de Thalès, \(AC\) et \(A'M\) sont parallèles, et \(BC\) et \(B'M\) sont parallèles.
\(M\) est donc à la fois sur \(B'C'\) et sur \(A'C'\), et donc \(M=C'\). On en déduit le résultat demandé.
Notez que là aussi on peut raisonner via des homothéties.
\(\bullet\)Second cas: \(AA'\) et \(BB'\) sont parallèles.
Alors \(\overrightarrow{AA'}=\overrightarrow{BB'}\), et on construit \(M\) tel que \(\overrightarrow{CM}=\overrightarrow{AA'}\); on a alors magiquement \(\overrightarrow{CM}=\overrightarrow{BB'}\), et donc \(A'M\) est parallèle à \(AC\) et \(B'M\) est parallèle à \(BC\); donc \(M=C'\).
Il y a une réciproque au théorème de Desargues, que nous allons maintenant voir. Un point très sympathique est le besoin de passer par la géométrie projective.
\(\boxcircle\) En géométrie projective
(Théorème de Desargues).
On se donne \(ABC\) et \(A'B'C'\) deux triangles d’un plan projectif. On note \(a\), \(b\) et \(c\) les points d’intersection respectifs de \(BC\) et \(B'C'\), \(AC\) et \(A'C'\), \(AB\) et \(A'B'\). Alors \(a\), \(b\) et \(c\) sont alignés si et seulement si \(AA'\), \(BB'\) et \(CC'\) sont concourantes.
Notez bien qu’il s’agit d’une généralisation du théorème précédent! Deux droites parallèles en géométrie affine se croisent à l’infini dans leur complété projectif.
Supposons tout d’abord \(a\), \(b\) et \(c\) alignés. Ils déterminent donc une droite. On peut supposer que cette droite est la droite à l’infini, puisque, comme on l’a déjà dit, n’importe quelle droite (ou hyperplan dans le cas général) peut être considérée comme droite (ou, donc, hyperplan dans le cas général) à l’infini.
Pour cela on va utiliser la dualité. En fait, il n’y a tout simplement rien à faire, car l’énoncé dual du théorème de Desargues, dans le sens où on l’a montré, est précisément sa réciproque.
\(O_2(\mathbb{R})\), \(O_3(\mathbb{R})\), les polygones réguliers, les polyèdres réguliers
\(O_2(\mathbb{R})\) et \(O_3(\mathbb{R})\) sont des notations classiques pour \(O(\mathbb{R}^2)\) et \(O(\mathbb{R}^3)\) respectivement. \(O_k^+(\mathbb{R})\), dit aussi \(SO_k(\mathbb{R})\), désigne l’ensemble des transformations orthogonales de déterminant positif de \(\mathbb{R}^k\).
De manière plus générique, \(O(E)\) désigne l’ensemble des matrices orthogonales de l’espace euclidien \(E\); \(SO(E)\) désigne l’ensemble des matrices orthogonales de déterminant positif de l’espace euclidien \(E\). Ces notions dépendent donc du produit scalaire considéré; implicitement, dans \(O(\mathbb{R}^k)=O_k(\mathbb{R})\) (groupe orthogonal) ou \(SO(\mathbb{R}^k)=O_k^+(\mathbb{R})\) (groupe spécial orthogonal), on considère le produit scalaire usuel.
Dimension \(2\)
\(\boxcircle\) Définition de la notion d’angle
On suppose \(\mathbb{R}^2\) orienté (par exemple par l’orientation usuelle, qui fait de \(((1,0),(0,1))\) une base orthonormée directe.
(Angle).
L’angle orienté entre deux vecteurs unitaires \(u\) et \(v\) de \(\mathbb{R}^2\) (pris dans cet ordre) est par définition l’unique rotation de \(\mathbb{R}^2\) par laquelle l’image de \(u\) est \(v\).
L’angle orienté entre deux vecteurs non nuls quelconques \(u\) et \(v\) de \(\mathbb{R}^2\) (pris dans cet ordre) est par définition l’angle orienté entre \(\frac{1}{{\parallel}u {\parallel}} u\) et \(\frac{1}{{\parallel}v {\parallel}} v\).
On appelle angle nul l’angle entre \(u\) et \(u\) pour \(u\) vecteur non nul quelconque (la notion ne dépend pas de \(u\)).
On appelle angle plat l’angle entre \(u\) et \(-u\) pour \(u\) vecteur non nul quelconque.
On appelle angle orienté de deux demi-droites\(\mathbb{R}^+ u\) et \(\mathbb{R}^+ v\) l’angle orienté entre \(u\) et \(v\).
Pour tous ces angles, l’angle non orienté correspondant est la paire \(\{r,r^{-1}\}\) avec \(r\) l’angle orienté correspondant.
L’angle orienté de deux droites \(\mathbb{R}u\) et \(\mathbb{R}v\) est la paire des angles entre \(\mathbb{R}^+ u\) et \(\mathbb{R}^+ v\) et entre \(\mathbb{R}^+ u\) et \(\mathbb{R}^- v\).
L’angle non-orienté correspondant est l’ensemble à \(4\) éléments (au plus) constitué des angles orientés entre \(\mathbb{R}^+ u\) et \(\mathbb{R}^+ v\), entre \(\mathbb{R}^+ u\) et \(\mathbb{R}^- v\), et leurs inverses.
Etant donnée une base orthonormée directe de \(\mathbb{R}^2\) et un angle orienté \(r\) entre demi-droites ou entre vecteurs, on appelle mesure de cet angle l’unique \(\theta\in \mathbb{R}/2\pi\mathbb{Z}\) tel que la matrice de \(r\) dans cette base soit \[\left( \begin{array}{cc} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \newline \end{array} \right)\]
Notons que la valeur de \(\theta\) est indépendante du choix de la base orthonormée directe.
On appelle mesure principale d’un angle la mesure de cet angle comprise dans \(]-\pi,\pi]\). On notera \(\widehat{X,Y}\) l’angle orienté entre \(X\) et \(Y\), quelle que soit la nature de \(X\) et \(Y\).
Notons que ces définitions restent valables en remplaçant \(\mathbb{R}^2\) par tout plan euclidien orienté.
\(\boxcircle\) Sous-groupes finis de \(O_2(\mathbb{R})\)
Tout sous-groupe fini de \(O_2^+(\mathbb{R})\) s’identifie à un sous-groupe fini de \(({\mathbb U},\times)\)4.
Un tel sous-groupe est donc de la forme \(\{e^{\frac{2ik\pi}n} ; k \in [\![0,n-1]\!]\}\), et est isomorphe à \(\mathbb{Z}/n\mathbb{Z}\), avec \(n\) l’ordre du groupe. Il est ainsi monogène et cyclique.
Tout sous-groupe fini de \(O_2(\mathbb{R})\) s’identifie à \(\mathbb{Z}/n\mathbb{Z}\) ou à \(D_n\simeq \mathbb{Z}/n\mathbb{Z}\rtimes \mathbb{Z}/2\mathbb{Z}\), groupe diédral d’ordre \(2n\).
Soit \(G\) un sous-groupe fini de \(O_2^+(\mathbb{R})\). Il est engendré par un nombre fini de rotations (puisqu’il n’y a que des rotations dans \(O_2^+(\mathbb{R})\)). Donc il est engendré par des rotations d’ordre fini, d’angle \(e^{\frac{2\pi}n}\). En posant \(m\) le \(ppcm\) des \(n\) en question, on constate que \(G\) est engendré par la rotation d’angle \(e^{\frac{2\pi}n}\).
On aurait aussi pu noter que \(O_2^+(\mathbb{R})\) est isomorphe à \(({\mathbb U},\times)\) (on associe la rotation d’angle \(\theta\) au complexe \(e^{i\theta}\). Considérons maintenant \(G\) un sous-groupe fini de \(O_2(\mathbb{R})\) et montrons qu’il est de l’une des deux formes annoncées. S’il est inclus dans \(O_2^+(\mathbb{R})\) c’est terminé. En cas contraire, soit \(s\) appartenant à \(G\cap O_2^-(\mathbb{R})\). \(s\) est une symétrie. L’intersection \(H\) de \(G\) et de \(O_2^+(\mathbb{R})\) est un sous-groupe fini de \(O_2^+(\mathbb{R})\); il est donc engendré par la rotation \(r\) d’angle \(2\pi/n\) pour un certain \(n\). Le groupe \(G\) est alors engendré par \(r\) et \(s\); \(G=H\cup sH=\{Id,s\}\times H\) (au sens du produit ensembliste et non du produit direct). \(H\) est distingué, \(\{Id,s\} \cap H=\{ Id \}\): donc \(G=\mathbb{Z}/2\mathbb{Z}\rtimes \mathbb{Z}/n\mathbb{Z}=D_n\).
\(\boxcircle\) Polygones réguliers
(droite de Simson).
On appelle polygone régulier de \(\mathbb{R}^2\) l’orbite d’un vecteur non nul sous l’action d’un sous-groupe fini de \(O_2^+(\mathbb{R})\).
On consultera la partie [diedral] pour constater que le groupe diédral \(D_n\) est isomorphe au groupe des isométries d’un polygone régulier.
On pourra consulter le livre [GIO] pour la constructibilité des polygones réguliers; la caractérisation des \(n\) tels que "le polygone régulier à \(n\) côtés est constructible" est très surprenante, et fait intervenir les nombres de Fermat: un tel polygone est constructible si \(n\) s’exprime comme le produit d’une puissance de \(2\) par un produit de nombres premiers de Fermat distincts5. Par exemple, le plus petit polygone régulier non constructible est l’heptagone.
Dimension \(3\) : Sous-groupes finis de \(O_3^+(\mathbb{R})\)
(Sous-groupes finis de \(O_3^+(\mathbb{R})\)).
Les sous-groupes finis de \(O_3^+(\mathbb{R})\) sont de l’une des 5 formes suivantes:
\(\bullet\)Groupes constitués exclusivement de rotations, isomorphes à \(\mathbb{Z}/n\mathbb{Z}\)
\(\bullet\)Groupes isomorphes aux groupes diédraux (ordre pair) Toutes les isométries des groupes d’un de ces deux premiers types ont la particularité de laisser stable une même droite \(D\), i.e. ce sont des isométries agissant dans le plan \(D^\perp\).
\(\bullet\)Groupe des isométries positives laissant invariant un tétraèdre régulier (ordre 12)
\(\bullet\)Groupe des isométries positives du cube = groupe des isométries positives de l’octaèdre (ordre 24)
\(\bullet\)Groupe des isométries positives de l’icosaèdre (ordre 60)
Il existe des exemples pour chacun de ces cas.
La démonstration de ce théorème serait bien trop longue pour la marge de ce livre. On pourra se référer au livre [GIO].
\(\boxcircle\) Polyèdres réguliers
On n’étudiera pas ici l’existence des 5 polyèdres réguliers et les relations de dualité. Le lecteur intéressé pourra se référer à [COM]; la preuve qui y est donnée est donnée de manière intuitive, car le formalisme nécessaire pour manier de tels objets est difficile, et il est sans doute préférable de se limiter à des notions intuitives.
Les 5 polyèdres réguliers sont le tétraèdre (4 faces triangulaires), le cube (6 faces carrées), l’octaèdre (8 faces triangulaires), l’icosaèdre (20 faces triangulaires), le dodécaèdre (12 faces pentagonales).
La droite de Simson et quelques suites
La droite de Simson, selon la rumeur, ne devrait en fait rien à Simson mais plutôt à Wallace, mais tous les auteurs ne sont pas de cet avis. On parlera ensuite du cercle dit "cercle des neufs points". Une autre étude classique est la droite de Steiner, dont nous ne parlerons pas ici. La version que nous donnons de ce théorème est une synthèse d’une partie du beau livre de Hahn, "Complex numbers and geometry". On peut trouver dans la littérature l’enveloppe des droites de Simson (quand \(D\) bouge).
Les-mathematiques.net
Les-mathematiques.net
Soit \(A,B,C\) un triangle, \(D\) un point (figure [sims], gauche). Soient \(P\), \(Q\) et \(R\) les projections orthogonales de \(D\) sur \((BC)\), \((CA)\) et \((AB)\). Alors \(P\),\(Q\) et \(R\) sont colinéaires \(\iff\)\(D\) appartient au cercle circonscrit à ABC.
On considère le triangle ABC inscrit dans un cercle de centre \(0\) et de rayon \(1\) (sans perte de généralité). On note \(\alpha\), \(\beta\), \(\gamma\), \(\delta\), \({\lambda}\), \(\mu\) et \(\nu\) les affixes respectives de \(A\),\(B\),\(C\),\(D\),\(P\),\(Q\),\(R\).
Une équation de \((BC)\) est donnée par le calcul suivant: \[z\in (BC) \iff \frac{z-\beta}{\gamma-\beta} \in \mathbb{R}\]\[\frac{z-\beta}{\gamma-\beta}=\frac{\overline z - \overline \beta}{\overline \gamma- \overline \beta}\] c’est-à-dire6\(z+\gamma.\beta.\overline z = \beta+ \overline \gamma\)
Une équation de \((PD)\) est: \[z\in (PD)\iff \frac{z-\delta}{\gamma- \beta} \in i\mathbb{R}\]\[\iff \frac{z-\delta}{\gamma-\beta}=-\frac{\overline z - \overline \delta}{\overline \gamma- \overline \beta}\]
Donc l’intersection de ces deux droites doit vérifier: \[z-\gamma.\beta.\overline z=\delta-\gamma.\beta.\overline \delta\]
On en déduit que \({\lambda}=\frac12(\beta+\gamma+\delta-\beta.\gamma.\overline \delta)\). De même: \[\mu=\frac12(\alpha+\gamma+\delta-\alpha.\gamma.\overline \delta),\ \nu=\frac12(\alpha+\beta+\delta-\alpha.\beta.\overline \delta)\]\[\begin{aligned}
\mbox{$P,Q,R$ colinéaires}& \iff& \frac{{\lambda}- \nu}{\mu - \nu} \in \mathbb{R},\\
&\iff& [\gamma,\frac \delta{|\delta|^2},\beta,\alpha] \in \mathbb{R}\\
&\iff& \alpha, \beta, \gamma, \frac \delta{|\delta|^2}\mbox{ cocycliques ou alignés}\\
&\iff& |\delta|=1\end{aligned}\]
Il s’agit des trois polynômes symétriques élémentaires en \(\alpha\), \(\beta\), \(\gamma\). Notons que \(\overline \sigma_1=\overline \alpha+\overline \beta+\overline \gamma=\frac1\alpha +\frac1\beta+\frac1\gamma=\frac{\sigma_2}{\sigma_3}\).
\(z=\frac12 (\sigma_1 + \delta- \alpha - \frac{\sigma_3}{\delta.\alpha})\) et \(\overline z = \frac12 (\sigma_2/\sigma_3 + 1/\delta- 1/\alpha - \frac{\delta.\alpha}{\sigma_3})\)
En éliminant \(\alpha\): \[\delta.z - \sigma_3.\overline z = \frac12 (\delta\sigma_1 + \delta^2 - \sigma_2 - \sigma_3/\delta)\] Cette expression, étant symétrique en \(\alpha\), \(\beta\), \(\gamma\), est vérifiée aussi pour \(\mu\) et \(\nu\). C’est l’équation d’un sous-espace affine, qui est : \(\bullet\)non vide \(\bullet\)non réduit à un point car \(P,Q,R\) ne sont jamais confondus. \(\bullet\)non égal au plan car \(\sigma_3\) est non nul
(Droite de Simson).
Cette équation est donc l’équation d’une droite, appelée droite de Simson.
Soient \(L,M,N\) trois points sur le cercle circonscrit à \(ABC\). Alors les trois droites de Simson correspondantes sont concourantes si et seulement si \(\widehat{AL}+\widehat{BM}+\widehat{CN}\) est nul modulo \(2\pi\).
Soient \(l,m,n\) les affixes respectives de \(L,M,N\).
\[l.z-\sigma_3.\overline z = \frac12(l^2+\sigma_1.l-\sigma_3-\sigma_3/l)\]\[m.z-\sigma_3.\overline z = \frac12(m^2+\sigma_1.m-\sigma_3-\sigma_3/m)\]\[n.z-\sigma_3.\overline z = \frac12(n^2+\sigma_1.n-\sigma_3-\sigma_3/n)\]
Les deux premières se coupent en \(z=\frac12(l+m+\sigma_1+\sigma_3/(l.m))\).
Les deux dernières se coupent en \(z=\frac12(m+n+\sigma_1+\sigma_3/(m.n))\).
La condition nécessaire et suffisante est donc \(l-n+\sigma_3.(n-l)/(l.m.n)=0\), c’est-à-dire \(\sigma_3=m.l.n\) ou encore \(\alpha.\beta.\gamma=l.m.n\), d’où le résultat par passage aux arguments.
Le cercle des neuf points, et une suite par Coolidge
Cette partie est, elle aussi, fortement inspirée du livre de Hahn "Complex Numbers and Geometry".
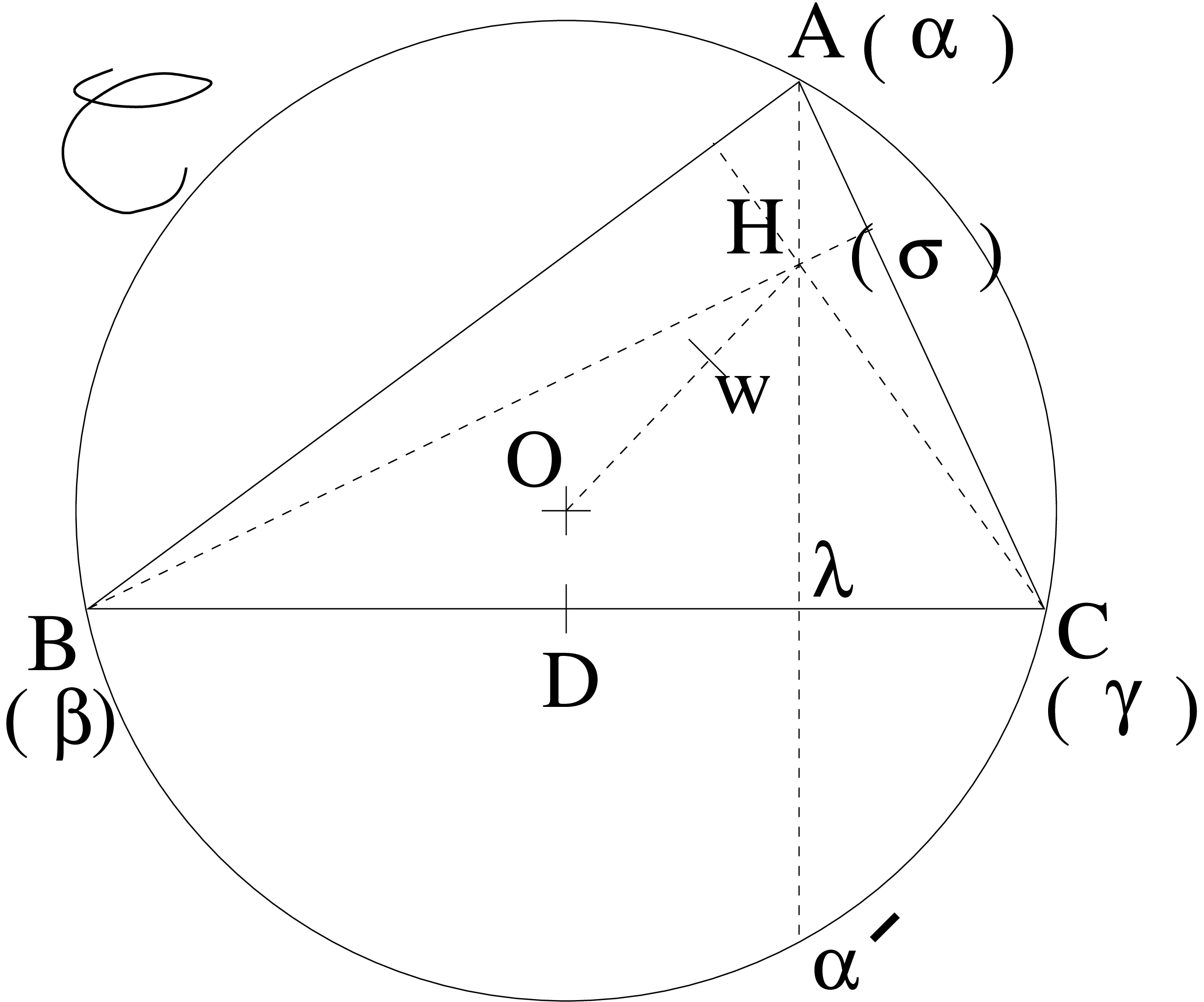
Soient \((ABC)\) un triangle, \(O\) le centre du cercle circonscrit, \(G\) le barycentre de \(A\), \(B\) et \(C\), et \(H\) l’intersection des hauteurs (figure [neuf], droite).
Alors: \(\bullet\)\((O,G,H)\) sont alignés. \(\bullet\)Les pieds des hauteurs, les milieux des côtés et les milieux des segments joignant l’orthocentre aux sommets \(A\), \(B\) et \(C\) sont tous sur un même cercle.
On choisit \(O\) pour origine du plan complexe.
On note \(\alpha,\beta,\gamma\) les affixes respectives de \(A,B,C\). On note \({\cal C}\) le cercle circonscrit, dont on suppose encore le rayon égal à 1, sans perte de généralité.
Soit \(H\) le point d’affixe \(\theta=\alpha+\beta+\gamma\). Comme \(\frac{\sigma-\alpha}2=\frac{\beta+\gamma}2\), on a \(\overrightarrow{AH}=2\overrightarrow{OD}\), où \(D\) est le milieu de \(BC\). En particulier, comme \(OA'\) est la médiatrice de \([BC]\), on a \((AH)\) et \((BC)\) orthogonales.
On peut raisonner de même pour obtenir \(BH \bot AC\) et \(CH \bot AB\); on retrouve ainsi le fait que les hauteurs sont concourantes en \(H\). Comme \(G\) a pour affixe \(\frac13 (\alpha+\beta+\gamma)\), les points \(O\), \(G\) et \(H\) sont alignés (et \(\overrightarrow{OH}=3\overrightarrow{OG}\)).
Soit \(W\) d’affixe \(\sigma/2\); \(W\) est le milieu de \([OH]\). \(WD=|\frac{\beta+\gamma}2 - \frac\sigma 2|=|\alpha|/2=\frac12\)
De même \(WE=WF=\frac12\) avec \(E\) et \(F\) les milieux respectifs de \([CA]\) et \([AB]\).
La distance de \(W\) au milieu de \(AH\) est elle aussi \(\frac12\), et de même pour les autres.
On note \({\Lambda}\) l’affixe du pied de la hauteur issue de \(A\).
Pour situer \({\Lambda}\) on va d’abord s’intéresser à \(\alpha '\), la seconde intersection de \(\alpha{\Lambda}\) avec \({\cal C}\). On va montrer que \(B\alpha '\sigma\) est isocèle. \(\overrightarrow{A\alpha '} \bot \overrightarrow{BC}\) donne \(\frac{\alpha ' - \alpha}{\gamma- \beta} \in i.\mathbb{R}\).
Lemme: On a \(\alpha'=-\frac{\beta\gamma}{\alpha}\).
begindivdemonstrationbegintext endtext Comme le quotient \(\frac{\beta\gamma}{\alpha \alpha'}\) est invariant par rotation, on peut supposer que \(\overrightarrow{A\alpha'}\) est vertical et \(\overrightarrow{BC}\) horizontal, de sorte que \(\alpha\alpha'=1\) et \(\beta\gamma=-1\), si bien que ce quotient vaut \(-1\) et \(\alpha'=-\frac{\beta\gamma}\alpha\) dans tous les cas.
On obtient donc par le lemme ci-dessus \(\alpha '=-\frac{\beta\gamma}\alpha\). On montre ensuite facilement que \(|B-\alpha'|=|B-\sigma|\), donc le triangle \(B\alpha '\sigma\) est isocèle. Le pied \(\lambda\) de la hauteur issue de \(A\) est en fait aussi le milieu de \([\alpha ' \sigma]\).
On en déduit alors que \(|{\Lambda}-\sigma/2|=1/2\). On ferait de même pour les pieds des autres hauteurs. Finalement \(\sigma/2\) est le centre d’un cercle de rayon \(1/2\) comportant les pieds des trois hauteurs, les milieux des trois côtés, et les milieux des segments joignants l’orthocentre aux sommets \(A\),\(B\) et \(C\) sont tous sur un même cercle.enddivdemonstration
Enfin, voici le résultat dû à Coolidge:
\(\bullet\)Soient \(z_1\),...,\(z_4\) sur le cercle unité. Le centre du cercle d’Euler de \(z_2,z_3,z_4\) est \(\tau_1=\frac12 (z_2+z_3+z_4)\); \(\tau_2\), \(\tau_3\), \(\tau_4\) sont définis de manière analogue. On définit en outre \(\tau=\frac14(z_1+z_2+z_3+z_4)\); alors pour tout \(i\), \(\tau_i\) est sur le cercle de centre \(\tau\) et de rayon \(\frac12\); ce cercle est appelé cercle d’Euler du quadrilatère \(z_1\),\(z_2\),\(z_3\),\(z_4\). \(\bullet\)On peut faire la même chose avec 5 points; on définit 5 cercles d’Euler de 5 quadrilatères, et un cercle d’Euler pour le pentagone. \(\bullet\)On peut procéder de même avec un polygone quelconque.
Pour plus de précisions, on pourra consulter le livre de Hahn cité ci-dessus.
1 Ceux qui n’ont pas étudié la géométrie projective peuvent penser aux paires de points antipodaux sur une sphère.
2 Précisément, on définit successivement \(d1\) comme la première dérivée non nulle et \(d_2\) comme la première dérivée non nulle et non colinéaire à \(d1\)
3 Ces deux triangles sont translatés l’un de l’autre ou homothétiques car directement semblables.
4 Groupe des nombres complexes de module \(1\), muni de la multiplication classique de \(\mathbb{C}\).
5 Un nombre premier de Fermat est un nombre premier de la forme \(2^{2^n}+1\). Les seuls nombres premiers de Fermat connus sont \(3\), \(5\), \(17\), \(257\), \(65537\).
6 En constatant que \(\frac{\alpha-\beta}{\overline \alpha-\overline \beta}=-\beta\gamma\) et \(\frac{\beta\overline \gamma-\overline \beta\gamma}{\overline \gamma-\beta}=\beta+\gamma\).
Bibliographie
[GIO] W. Giorgi, Thèmes mathématiques pour l’agrégation, Masson, 1998.
[COM] F. CombesAlgèbre et géométrie, Bréal, 1998.
Barre utilisateur
[ID: 53] [Date de publication: 26 avril 2021 21:45] [Catégorie(s): Le cours d'agrégation ] [
Nombre commentaires: 0] [nombre d'éditeurs:
1 ] [Editeur(s): Emmanuel Vieillard-Baron ]
[nombre d'auteurs:
5 ] [Auteur(s): Christophe Antonini Olivier Teytaud Pierre Borgnat Annie Chateau Edouard Lebeau ]
