Un chapitre consacré au calcul différentiel. On y introduit les notions de différentielle, de dérivées partielles. Le chapitre est ponctué par deux théorèmes fondamentaux: le théorème d’inversion locale et le théorème des fonctions implicites.
Calcul différentiel
Il est recommandé de bien maîtriser la partie [topo] avant d’étudier cette partie, et notamment les espaces de Banach. On pourra alors dans ce chapitre, après l’introduction, plonger dans le théorème des accroissements finis, d’inversion locale, des fonctions implicites, dans aussi les dérivées d’ordre supérieur, avant un peu de zoologie pour finir.
Introduction
Généralités
\(\bullet\)La dérivée de \(f\) est unique et \[Df(x)(h)=lim_{t \rightarrow 0} \frac{f(x+t.h)-f(x)}t\] \(\bullet\)La notion de dérivée ne dépend que des topologies et pas des normes (du moment qu’elles définissent la même topologie); si deux normes sont équivalentes, alors une fonction différentiable pour l’une est différentiable pour l’autre, et la différentielle est la même.
\(\bullet\)\(D({\lambda}f + \mu g)(x)={\lambda}Df(x) + \mu Dg(x)\)
\(\bullet\)Si \(E=K\) corps associé aux espaces vectoriels \(E\) et \(F\), alors la différentiabilité équivaut à l’existence de la limite pour \(t \rightarrow 0\) de \(\frac{f(x+t)-f(x)}t\). On note alors cette limite \(f'(x)\), et \(Df(x)(t)=t.f'(x)\).
\(\bullet\)L’application qui à une application différentiable en \(x_0\) associe sa différentielle en \(x_0\) est une application linéaire de l’espace vectoriel des applications de \(E\) dans \(F\) différentiables en \(x_0\) dans l’espace vectoriel des applications linéaires de \(E\) dans \(F\).
\(\bullet\)Si \(f\) est constante, alors \(f\) est \(C^1\) et sa dérivée est nulle partout.
\(\bullet\)Si \(\phi\) de \(E\) dans \(F\) est linéaire continue, alors \(\phi\) est \(C^1\) avec \(D\phi(x)=\phi\), pour tout \(x\).
Soit \(u_0\) un isomorphisme de \(E\) vers \(F\); alors \(u_0+v=u_0.(Id+u_0^{-1}.v)\). Si \(\parallel v \parallel < \parallel u_0^{-1} \parallel^{-1}\), on a \(\parallel u_0^{-1}.v \parallel < 1\), et donc la série \[\sum_{i=0}^{+\infty} (-u_0^{-1}.v)^i\] est convergente dans \({\cal L}(E)\) et sa somme donne un inverse à \((Id+u_0^{-1}.v)\).
Donc pour \(\parallel v \parallel < \parallel u_0^{-1} \parallel^{-1}\), l’inverse de \(u_0+v\) est \(\sum_{i=0}^{+\infty} (-u_0^{-1}.v)^i.u_0^{-1}\).
Applications à valeurs dans un produit d’espaces vectoriels normés
Applications de plusieurs variables et dérivées partielles
Pour la cohérence de la définition, il convient de vérifier que les fonctions partielles \(x_1\mapsto f(x_1,a_2)\) et \(x_2\mapsto f(a_1,x_2)\) sont différentiables.
On note \(p_i(x_1,...,x_n)=x_i\).
On peut noter que dans le cas \(m=1\), la jacobienne s’identifie au gradient.
On peut définir de même une matrice pour la dérivée seconde si l’application est à valeurs de \(\mathbb{R}^n\) dans \(\mathbb{R}\); cette matrice s’appelle la matrice hessienne, voir la section [blon3].
Le théorème des accroissements finis
On présente ici l’important théorème des accroissements finis. Son intérêt sera montré par des sections d’applications (interversion de limite et de dérivation, et existence de dérivées à partir d’existence de dérivées locales), mais aussi par un grand nombre de références (\(\Arrowvert\)), dont tout ce qui concerne les développements de Taylor.
Résultats principaux
Voyons trois corollaires:
Applications : interversion de limite et de dérivation
\(\bullet\)\(f\) est différentiable et \(Df=g\).
\(\bullet\)Pour tout \(C\) convexe et borné inclus dans \(U\) la convergence de \({f_n}_{|C}\) vers \(f_{|C}\) est uniforme.
On suppose \(U\) connexe ouvert de \(E\) et \(f_n\) de \(U\) dans \(F\) différentiable; \(E\) et \(F\) sont des espaces vectoriels normés , et \(F\) est complet (\(F\) est un Banach). On suppose qu’il existe \(x_0\) tel que \(f_n(x_0)\) converge, et que pour tout \(x\) il existe \(V_x\) voisinage de \(x\) tel que la suite des \({Df_n}_{|V_x}\) soit de Cauchy pour la distance \(d\) définie par \[d(f,g) = sup_{z \in V_x} {\parallel}f(z)-g(z){\parallel}\] (c’est-à-dire que la suite des \(Df_n\) converge normalement sur un certain voisinage de tout point)
On définit alors \(\alpha_{n,m}=sup_{z \in V_x} {\parallel}Df_n(z)-Df_m(z) {\parallel}\); par hypothèse, \(\alpha_{n,m}\) tend vers \(0\) quand \(n\) et \(m\) tendent vers l’infini. Si \(V_x\cap A \neq \emptyset\), alors soit \(x'\) dans \(V_x \cap A\). Par convexité de \(V_x\), en utilisant le corollaire [co827], on peut écrire pour tout \(y\) dans \(V_x\): \[{\parallel}[f_m(y)-f_n(y)] - [f_m(x')-f_n(x')] {\parallel}\leq \alpha_{n,m}.{\parallel}y - x' {\parallel}\] or \(f_n(x')\) est une suite de Cauchy (comme toute suite convergente dans un métrique), donc \(f_n(y)\) est une suite de Cauchy, et donc converge. Donc si \(V_x \cap A \neq \emptyset\), \(V_x \subset A\). Donc tout point de \(A\) possède un voisinage \(V_x\) contenu soit dans \(A\) soit dans \(A^c\), ce qui montre que \(A\) et \(A^c\) sont ouverts. \(A\) étant non vide et \(U\) étant connexe, \(A=U\). On a donc montré que la suite des \(f_n\) converge simplement.
Applications : dérivées partielles et dérivées
\(\bullet\)Il est suffisant de montrer que \[{\parallel}f(x_1,...,x_n)-f(a_1,...,a_n) - \sum_{i=1}^n \frac{\delta f}{\delta x_i}(a).(x_i-a){\parallel}= o({\parallel}x-a {\parallel})\] pour tout \((a_1,...,a_n)\) de \(U\).
\(\bullet\)Pour cela on décompose \(f(x_1,...,x_n)-f(a_1,...,a_n) - \sum_{i=1}^n \frac{\delta f}{\delta x_i}(a).(x_i-a)\) en \[\begin{aligned} & &f(x_1,...,x_n)-f(a_1,x_2,...,x_n)-\frac{\delta f}{\delta x_1}(a).(x_1-a_1)\\ &+&f(a_1,x_2,...,x_n)-f(a_1,a_2,x_3,...,x_n)-\frac{\delta f}{\delta x_2}(a).(x_2-a_2)\\ &+&...\\ &+&f(a_1,a_2,...,a_i,x_{i+1},...,x_n)-f(a_1,...,a_{i+1},x_{i+2},...,x_n)\\ & & -\frac{\delta f}{\delta x_{i+1}}(a).(x_{i+1}-a_{i+1})\\ &+&...\newline &+&f(a_1,a_2,...,a_{n-1},x_n)-f(a_1,...,a_n)-\frac{\delta f}{\delta x_n}(a).(x_n-a_n)\end{aligned}\] \(\bullet\)Il suffit ensuite de montrer que pour \(x_i\) tendant vers \(a_i\), \(f(a_1,a_2,...,a_{i-1},x_i,...,x_n)-f(a_1,...,a_i,x_{i+1},...,x_n)-\frac{\delta f}{\delta x_i}(a).(x_i-a_i)\) est un \(o(x_i-a_i)\). (ensuite il suffira de sommer)
Théorème d’inversion locale et fonctions implicites
On va voir ici d’importants théorème: le théorèmes d’inversion globale, d’inversion locale, de fonctions implicites. Ces théorèmes sont notamment fondamentaux pour
calculer des différentielles d’inverse, ce qui peut être très pratique pour mettre à jour des solutions de problèmes inverses (théorème d’inversion locale).
établir qu’un \(C^1\)-difféomorphisme de classe \(C^n\) est en fait un \(C^n\)-difféomorphisme (conséquence du théorème d’inversion globale).
établir que toute application d’un espace euclidien dans lui-même dont la différentielle existe, est continue et est un endormophisme orthogonal en chaque point, est une isométrie affine (ce qui permettra d’étudier des propriétés métriques d’un sous-ensemble d’un espace euclidien en se ramenant à son image ou son image inverse par une telle application).
Théorème d’inversion globale
Le théorème d’inversion globale est notamment important pour construire le théorème d’inversion locale, mais il a aussi des corollaires propres distincts comme on va le voir.
Soit \(X\) un espace métrique complet et \(h\) une contraction de \(X\) dans \(X\). Alors:
\(\bullet\)\(h\) admet un unique point fixe \(x_0\)
\(\bullet\)Si \(x_1\) et \(x_2\) sont deux points fixes de \(f\), on a alors :
\(d(x_1,x_2)=d(h(x_1),h(x_2))\leq Lip(h).d(x_1,x_2)\), donc \(x_1=x_2\)
Existence:
\(\bullet\)Considérons \(x\) quelconque dans \(X\), on va travailler sur la suite des \(h^n(x)\).
\(\bullet\)\(Dh(x_0)\) est un isomorphisme de \(E\) sur \(F\);
\(\bullet\)On dérive les deux expressions \[h^{-1}\circ h = Id_E\mbox{ et } h \circ h^{-1} = Id_E\] et on montre bien que \(Dh(x_0)\) est un isomorphisme.
\(\bullet\)Par définition de la dérivée, la quantité ci-dessous tend vers \(0\) pour \(y \to h(x_0)\): \[\frac{{\parallel}h^{-1}(y)-h^{-1}(h(x_0)) - D(h^{-1})(h(x_0))(y-h(x_0)) {\parallel}}{{\parallel}y - h(x_0) {\parallel}}\] Donc pour \(y\) dans un certain \(W\) cette quantité est plus petite que \(1\), et donc pour \(y \in W\) on a \[{\parallel}h^{-1}(y) - h^{-1}(h(x_0)) {\parallel}\leq K {\parallel}y - h(x_0) {\parallel}\] avec \(K=1+{\parallel}D(h^{-1})(h(x_0)){\parallel}\).
Il reste à prouver la réciproque, c’est-à-dire que les conditions sont suffisantes.
\(\bullet\)Par définition, on a \[h(x)-h(x_0)=Dh(x_0)(x-x_0)+{\parallel}x - x_0 {\parallel}\epsilon(x)\] avec \(\epsilon(x)\) tendant vers \(0\) pour \(x \to x_0\).
Soit \(A\) une application linéaire continue de \(E\) dans \(F\), avec \(E\) un espace de Banach et \(F\) un espace normé, telle que \(A^{-1}\) existe et est continue (\(A\) est un homéomorphisme linéaire). Soit \(\phi\) une application lipschitzienne de \(E\) dans \(F\) telle que \(Lip(\phi) < {\parallel}A^{-1} {\parallel}^{-1}\). Alors:
\(\bullet\)\(h=A+\phi\) est inversible.
\(\bullet\)\(h^{-1}\) est lipschitzienne, avec \(Lip(h^{-1}) \leq \frac{{\parallel}A^{-1} {\parallel}}{[1-{\parallel}A^{-1} {\parallel}. Lip(\phi)]}\)
\(\bullet\)Étant donné \(y\) dans \(F\), et on considère l’équation \[h(x)=y\] équivalente à \[x=A^{-1}.y-A^{-1}(\phi(x))\] L’application \(x \mapsto A^{-1}(\phi(x))\) est Lipschitzienne de rapport \(<1\), donc l’application \(x \mapsto A^{-1}(y)- A^{-1}(\phi(x))\) aussi. Donc par le théorème du point fixe de Banach, cette équation a une solution unique \(x\).
\(h\) est donc inversible.
\(\bullet\)Avec \(y=h(x)\) et \(y'=h(x')\), on peut écrire \[x=A^{-1}(y)-A^{-1}(\phi(x))\] \[x'=A^{-1}(y')-A^{-1}(\phi(x'))\] et en déduire \[{\parallel}x - x' {\parallel}\leq {\parallel}A^{-1} {\parallel}. {\parallel}y - y' {\parallel}+ {\parallel} A^{-1} {\parallel}.Lip(\phi).{\parallel}x - x' {\parallel}\] en utilisant l’hypothèse sur \(Lip(\phi)\), on a alors \[{\parallel}x-x' {\parallel}\leq \frac{{\parallel}A^{-1} {\parallel}}{1-{\parallel} A^{-1}{\parallel}.Lip(\phi)}{\parallel}y-y' {\parallel}\] D’où le résultat sur la constante de Lipschitz de \(h^{-1}\).
Théorème d’inversion locale
Le théorème d’inversion locale est important en soi (il permet de calculer des différentielles d’inverses) mais aussi en tant qu’outil pour construire le théorème des fonctions implicites.
Soit \(f\) une application \(C^1\) d’un ouvert \(U\) d’un espace de Banach \(E\) dans un espace de Banach \(F\); si \(f\) injective et si sa différentielle \(f'(x)\) est un isomorphisme en tout \(x\in U\), alors \(f\) est un \(C^1\)-difféomorphisme de \(U\) sur \(f(U)\), qui est alors un ouvert de \(F\).
Une extension est possible: modulo le résultat selon lequel l’application \(Inv\) qui à \(f\) dans \(Isom(E,F)\) associe \(f^{-1}\) est \(C^\infty\) (que l’on trouvera par exemple dans [CAR]), on montre que si \(f\) est un \(C^1\)-difféomorphisme de classe \(C^n\), alors \(f\) est un \(C^n\)-difféomorphisme.
Soit \(x\) un point de \(E\). Comme \(Df(x)\) est inversible, d’après le théorème d’inversion locale, il existe une boule \(B\) centrée en \(x\) telle que \(f\) induit un \(C^1\)-difféomorphisme de \(B\) sur \(f(B)\). Pour tout \(y\) dans \(f(B)\), la différentielle \(D(f^{-1})(y)=(Df(f^{-1}(y)))^{-1}\) est un endomorphisme orthogonal, si bien que la réciproque de \(f\) de \(f(B)\) vers \(B\) est également \(1\)-lipschitzienne. Par double inégalité, la restriction de \(f\) à \(B\) est une isométrie.
Théorème des fonctions implicites
\(\bullet\)On va chercher à utiliser le théorème d’inversion locale. Pour cela il faut construire une application différentiable \(C^1\), de différentielle bijective.
\(\bullet\)On définit l’application \(\mu\) de \(U\) dans \(E_1\times E_2\) dans \(E_1 \times G\), définie par \(\mu(y_1,y_2)=(y_1,f(y_1,y_2))\).
\(\bullet\)\(D\mu(a,b)(h,k)=(h,D_1f(a,b).h+D_2f(a,b).k)\)
\(\bullet\)\(D\mu(a,b)\) est bijective (facile), \(\mu\) est \(C^1\)
\(\bullet\)On applique le théorème d’inversion locale à \(\mu\) en \((a,b)\).
La figure [implic] illustre ce théorème.
Commentaire: Illustration du théorème des fonctions implicites dans le cas d’une fonction de \(\mathbb{R}^2\) dans \(\mathbb{R}\). La courbe est une courbe de niveau. A gauche la différentielle par rapport à \(y\) n’est pas un isomorphisme; on comprend intuitivement qu’on ne peut pas donner \(y\) en fonction de \(x\) sur un voisinage. A droite c’est un isomorphisme; donc on peut.
Dérivées d’ordre supérieur
Les dérivées d’ordre élevé permettent de nombreuses choses; par exemple, les algorithmes d’optimisation basés sur la hessienne ont des ordres de convergence largement supérieurs aux méthodes basées sur le seul gradient. De même, les schémas d’intégration numérique sont bien plus rapides théoriquement en ayant un ordre élevé (i.e. en utilisant une dérivée 3ème, 4ème). Il faut bien noter toutefois qu’une dérivée troisième, quatrième, cinquième, est bien instable et difficile à calculer. Ainsi, sur les machines de précision finie, on n’utilisera jamais, pour l’optimisation, une dérivée 3ème car elle est trop chère à calculer, et en intégration numérique (où la dérivée \(k\)-ième est utilisée pour démontrer les convergences mais n’est pas explicitement calculée) on s’arrête en général à \(4\) car le calcul devient instable ensuite. Ce problème de dérivée inutilisable ou trop chère est tel que de nombreuses méthodes d’optimisation se passent désormais de dérivées (méthodes évolutionnaires, méthodes de recuit simulé), et de même des méthodes de calcul d’intégrale, notamment quand la dimension augmente, se contentent de moyenner des valeurs ayant toutes exactement le même poids (i.e. \(\int f\) est approximé par \(\frac1n\sum_{i=1}^n f(x_i)\), typiquement avec des méthodes de Monte-Carlo ou Quasi-Monte-Carlo, au lieu de \(\sum_{i=1}^n w_i f(x_i)\) avec \(\sum w_i=1\) et \(w_i\) parfois négatif lorsqu’on utilise des schémas numériques d’intégration basés sur les développements de Taylor).
Généralités
On note alors \(f^{(1)}(a)\) l’application \(Df(a)(x)\), et par récurrence \(f^{(n)}(a)\) l’application \(Df^{(n-1)}(a)\).
Étant donné une application \(f\) d’un ouvert \(U\) d’un espace de Banach \(E\) dans un espace de Banach \(F\), on dit que \(f\) est \(n\) fois différentiable en \(x\) appartenant à \(U\) si et seulement si \(f\) est de classe \(C^{n-1}\) sur un voisinage de \(x\) et si la \(n\)-ième différentielle de \(f\) sur ce voisinage est différentiable en \(a\).
Notez l’ordre dans la définition: on a besoin de différentielle (\(n\) fois) sur un ouvert pour définir la différentielle en un point \(n+1\) fois.
Dérivées secondes
\(\bullet\)Il s’agit donc de montrer que \(f''(a)(h)(k)=f''(a)(k)(h)\).
\(\bullet\)On introduit la fonction \(\mu(h,k)=f(a+h+k)-f(a+h)-f(a+k)+f(a)\)
\(\bullet\)\(\mu(h,k)=\mu(k,h)\) clairement
\(\bullet\)On montre maintenant que \(\mu(h,k)\) approche \(f''(a)(h)(k)\) (on pourra plus loin en déduire le résultat souhaité, car \(f''(a)(h)(k)\) approchera alors \(f''(a)(k)(h)\))
\(\bullet\)\({\parallel}\mu(h,k)-f''(a)(h)(k) {\parallel}\leq {\parallel}\mu(h,k)-f'(a+k)(h)+f'(a)(h) {\parallel}+ {\parallel} f'(a+k)(h)-f'(a)(h)-(f''(a).k).h {\parallel}\)
\(\bullet\)Le second terme est petit par la définition de la différentielle \(f''(a)\), le premier est petit par définition de la différentielle de \(f'(a)\), et par utilisation des accroissements finis.
\(\bullet\)On arrive ainsi à montrer que \(\mu(h,k)-f''(a)(k)(h)\) est un \(o({\parallel}h {\parallel}^2 + {\parallel}k {\parallel}^2)\); par symétrie on a aussi le fait que \(\mu(h,k)-f''(a)(k)(h)\) est un \(o({\parallel}h {\parallel}^2 +{\parallel}k {\parallel}^2)\); on en déduit \({\parallel}f''(a)(k)(h)-f''(a)(h)(k) {\parallel}= o( {\parallel}h {\parallel}^2 + {\parallel}k {\parallel}^2)\).
\(\bullet\)\({\parallel}f''(a)({\lambda}.k)({\lambda}.h)-f''(a)({\lambda}.h)({\lambda}.k) {\parallel}\leq \epsilon. ({\parallel}{\lambda}.h {\parallel}^2+{\parallel}{\lambda}.k {\parallel}^2)\) pour tout \(\epsilon\), pour \({\lambda}\) suffisamment petit
\(\bullet\)\({\lambda}^2 {\parallel}f''(a)(k)(h)-f''(a)(h)(k) {\parallel}\leq \epsilon.{\lambda}^2 ({\parallel}h {\parallel}^2 + {\parallel}k {\parallel}^2)\) pour tout \(\epsilon\) et pour \({\lambda}\) assez petit
\(\bullet\)\({\parallel}f''(a)(k)(h)-f''(a)(h)(k) {\parallel}\leq \epsilon({\parallel}h {\parallel}^2 + {\parallel}k {\parallel}^2)\) pour tout \(\epsilon\) !
Généralisations à la dérivée \(n\)-ième
On pourra si nécessaire réviser le chapitre [algmultilin] (algèbre multilinéaire) avant de plonger ici. Dans les applications informatiques en optimisation non-linéaire, souvent on s’arrête à la dérivée première, la dérivée seconde (la hessienne) étant approchée à partir de valeurs successives de la dérivée première (le gradient). Mais même sans calcul explicite des dérivées \(n\)-ième, on utilise parfois implicitement ces dérivées, par exemple pour estimer les erreurs de schémas d’intégrations numériques (par exemple, dérivée 6-ième pour la méthode dite de Boole-Villarceau, 4-ième pour Newton-Cotes).
\(\bullet\)Il suffit de montrer que si l’on permute deux variables consécutives parmi les \(h_i\) on ne change pas la valeur \(f^{(n)}(x)(h_1,...,h_n)\).
\(\bullet\)\(f^{(n-1)}\) est symétrique, donc on peut permuter sans rien changer \(h_i\) et \(h_{i+1}\) pour \(i>1\)
Zoologie du calcul différentiel
On présentera ici la convexité (fondamentale pour l’optimisation numérique et pour beaucoup d’autres choses), une fonction pathologique continue partout et dérivable nulle part, une autre fonction pathologique dérivable dans toutes les directions mais non continue, avant de passer à l’étude de variétés et de surfaces régulières.
Fonctions convexes
Dans la suite de cette section, on suppose que \(U\) est un convexe d’un espace vectoriel et que \(f\) est une application de \(\Omega\) dans \(\mathbb{R}\), avec \(\Omega\) ouvert contenant \(U\). Les liens entre dérivabilité et convexité sont les suivants:
\(f\) \(C^2\) est convexe si et seulement si \[\forall (u,v) \in U^2,\ f''(u)(v-u,v-u) \geq 0\]
Intuition Ce résultat généralise le cas standard d’une dérivée seconde positive comme critère de convexité pour \(U=]a,b[\subset \mathbb{R}\). \(f''(u)\) est simplement de la forme \(t\mapsto at^2\), avec \(a\) la dérivée seconde.
Intuition L’hypothèse de convexité de \(U\) est nécessaire. Un exemple de fonction non convexe ayant sa différentielle seconde strictement positive est: \(f(x)=x^2\) si \(x\in [-1,1]\) et \(f(x)=(x-3)^2\) si \(x\in [2,4]\).
Fonction continue partout dérivable nulle part
Cet exemple, élaboré par M. Van der Waerden, est extrait du livre [VP] auquel on se réfèrera pour plus de précisions que la brève présentation qui est faite ici.
Soit \(T\) la fonction définie sur \(\mathbb{R}\) par \(T(x)=min(x-E(x),E(x)+1-x)\) (c’est-à-dire que \(T(x)\) est la distance de \(x\) à l’entier le plus proche de \(x\)).
\(\bullet\)Il convient tout d’abord de vérifier que \(f\) est bien définie et continue: pour cela, il suffit de voir que \(f\) est limite uniforme d’une suite de fonctions continues (voir proposition [limcon]).
\(\bullet\)La non-dérivabilité est plus dure à établir:
\(T\), et donc \(f\), est périodique, de période \(1\).
On se limite donc à montrer la non-dérivabilité sur \([0,1[\)
On note les développements décimaux en excluant les développements illimités ne comportant que des \(9\) à partir d’un certain rang1
Soit donc \(x\in [0,1[\), on montre la non-dérivabilité de \(f\) en \(x\).
Soit \(x_n\) la \(n\)-ième décimale de \(x\).
définissons \(h_m=-10^{-m}\) si \(x_m=4\) ou \(x_m=9\), \(h_m=10^{-m}\) sinon.
Calculons maintenant \[\Delta_m=\frac{f(x+h_m)-f(x)}{h_m}\] \[\Delta_m= \sum_{n=1}^\infty \pm 10^{m-n}(T(10^nx\pm 10^{n-m})-T(10^nx)).\]
Pour \(n\geq m\), \(T(10^nx\pm 10^{n-m})-T(10^nx)\) est nul, car \(10^nx\pm 10^{n-m}\) et \(10^{nx}\) ont la même partie fractionnaire.
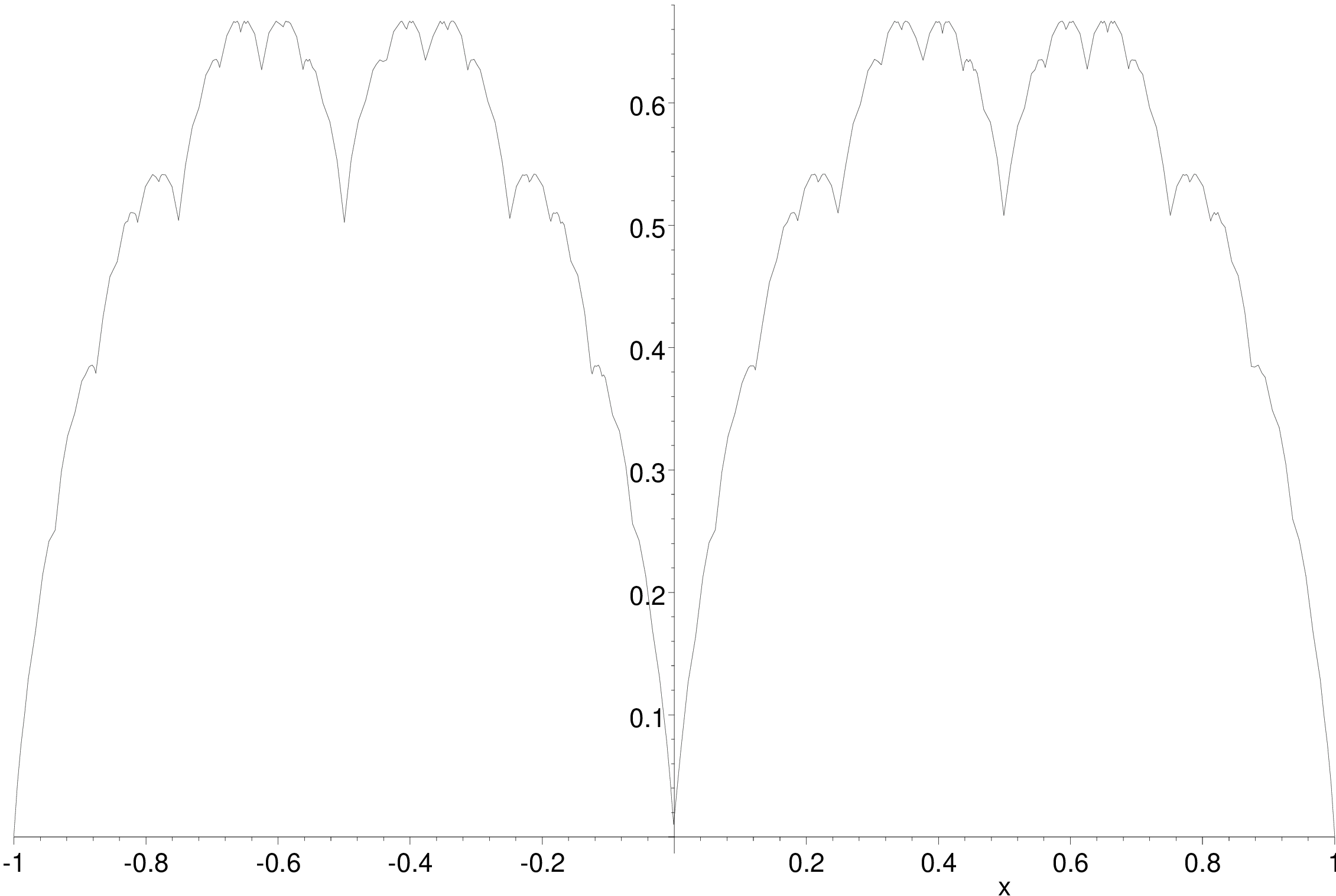
On en profite pour montrer ce dont est capable Maple. Le dessin se trouve en figure [conpasde].
| Exemple Maple |
|---|
\(>T := x\rightarrow \mathrm{min}(x - \mathrm{floor}(x), \,\mathrm{floor}(x) + 1 - x)\) \(T := x\rightarrow \mathrm{min}(x - \mathrm{floor}(x), \,\mathrm{floor}(x) + 1 - x)\) \(>g := x-> sum(T(2^n*x)/2^n,n=0..17);\) \(g := x\rightarrow {\displaystyle \sum _{n=0}^{17}} \,{\displaystyle \frac {\mathrm{T}(2^{n}\,x)}{2^{n}}}\) |
Tracé d’une courbe continue dérivable nulle part, établie par Van der Waerden.
Fonction dérivable dans toutes les directions mais non continue
Sous-variétés de \(\mathbb{R}^n\)
Soit \(M\) une partie de \(\mathbb{R}^n\), \(x\) un point de \(M\). Soit \(p\) un entier \(>0\) et \(k\) un entier \(>0\).
\(M\) est par définition une variété de dimension \(p\) et de classe \(C^k\) au voisinage de \(x\) si l’une des conditions équivalentes suivantes est vérifiée:
(i) Il existe \(V\) voisinage ouvert de \(x\) tel qu’il existe un \(C^k\) difféomorphisme de \(V\) sur \(W\subset \mathbb{R}^n\) tel que \(g(x)=0\) et \(g(M\cap V)=W\cap P\), avec \(P\) l’ensemble des \((y_1,...,y_n)\) tels que \(y_{p+1}=0\), \(y_{p+2}=0\), ... , \(y_n=0\).
(ii) Après une permutation pertinente des coordonnées \((x_1,...,x_n)\), il existe \(V\) voisinage ouvert de \(x\) et \(\phi\) application \(C^k\) de \(\mathbb{R}^p\) dans \(\mathbb{R}^{n-p}\) tel que pour tout \(y\) dans \(V\) \[y\in M \iff \phi(y_1,...,y_p)=(y_{p+1},...,y_n)\]
(iii) Il existe un voisinage \(V\) ouvert de \(x\), \(\Omega\) un voisinage ouvert de \(0\) dans \(\mathbb{R}^p\), \(f\) une application \(C^k\) de \(\Omega\) dans \(\mathbb{R}^n\), tels que \(f\) induise un homéomorphisme de \(\Omega\) sur \(M \cap V\), \(f(0)=x\) et \(f'(0)\) de rang \(p\) 2. Cette application est appelée représentation paramétrique locale de la variété.
(iv) Il existe un voisinage \(V\) ouvert de \(x\), \(\Omega\) un voisinage ouvert de \(0\) dans \(\mathbb{R}^p\), \(f\) une application \(C^k\) de \(\Omega\) dans \(\mathbb{R}^n\), tels que \(f\) induise un homéomorphisme de \(\Omega\) sur \(M \cap V\), \(f(0)=x\) et \(f'(y)\) de rang \(p\) pour tout \(y\) dans \(\Omega\) 3.
On notera pendant cette preuve \(x_{|I}\), avec \(I=\{i_1,...,i_m\}\) et \(i_1 < i_2 < \dots < i_m\) un sous-ensemble de \([1,n]\) et \(x\) un élément de \(\mathbb{R}^n\), \((x_{i_1},\dots,x_{i_m})\).
\(\bullet\)L’équivalence entre (iii) et (iv) est claire; bien sûr (iv) implique (iii), et réciproquement en supposant (iii) par continuité de la différentielle et continuité du déterminant d’une matrice extraite, on peut trouver un voisinage de \(0\) dans lequel la différentielle a le même rang. Il suffit alors de se restreindre à ce voisinage.
\(\bullet\)Voyons maintenant que (iii) implique (ii).
Supposons (iii). La matrice de la différentielle de \(f\) en \(0\) est de rang \(p\); modulo une bonne permutation des coordonnées, on peut donc supposer que la matrice extraite de la différentielle pour les indices en ligne et en colonne inférieurs ou égaux à \(p\) est inversible.
En se restreignant aux \(p\) première coordonnées, \(f\) est alors \(C^k\), de différentielle en \(0\) de rang plein. On peut donc appliquer le théorème d’inversion locale [invloc], et \(f\) ainsi restreint est donc un \(C^k\) difféomorphisme au voisinage de \(0\). En prenant \(\phi\) la composée de \(f\) et de l’inverse de la restriction de \(f\) aux \(p\)-premières coordonnées, on obtient une fonction satisfaisant (ii).
\(\bullet\)Voyons maintenant (ii) implique (iii).
Supposons (ii) vérifiée. Définissons alors \(f(y)=(y+x_{|[1,p]}, \phi(y+x_{|[1,p]})\)4. \(f\) convient.
\(\bullet\)Montrons maintenant que (iii) implique (i).
Supposons (iii) vérifiée.
Définissons alors \(g(y)=(y_{|[1,p]}-x_{|[1,p]},y_{|[p+1,n]}-\phi(y_{|[1,p]})\)... \(g\) convient pour (i).
\(\bullet\)Il ne reste plus qu’à vérifier que (i) implique (iii).
Supposons donc (i) vérifiée.
Alors soit \(f(y)=g^{-1}(y_{|[1,p]},0,\dots,0)\).
Surfaces régulières de \(\mathbb{R}^3\)
En général, on peut travailler dans \(\mathbb{R}^n\), mais pour la clarté du propos on se restreint ici aux surfaces de \(\mathbb{R}^3\).
On note les points suivants:
Le plan tangent ne dépend pas de la représentation paramétrique choisie.
Pour tout arc à valeurs dans la surface, le vecteur vitesse (la dérivée) est à valeurs dans la direction du plan tangent.
Toute solution d’une équation \(f(x,y,z)=0\) où \(f\) est \(C^k\) et de différentielle non nulle sur la ligne de niveau \(f^{-1}(0)\) est une surface régulière de \(\mathbb{R}^3\) (par le théorème des fonctions implicites [fonimp]).
La sphère de centre \(0\) et de rayon \(1\) n’admet pas de représentation paramétrique globale. Autrement dit, il n’existe pas d’homéomorphisme dont la différentielle est de rang \(2\) d’un ouvert de \(\mathbb{R}^2\) dans \(\mathbb{R}^3\), dont l’image soit exactement la sphère. Par contre, la sphère admet une représentation implicite \(x^2+y^2+z^2=1\).
On parle de surface régulière avec singularité lorsque la surface est une variété de classe \(C^k\) sauf en un nombre fini ou dénombrable de points, appelés singularités.
On peut toujours, étant donnée une surface régulière \(S\) de classe au moins \(C^1\) avec \(0\in S\) et tangente au plan \(z=0\) choisir une représentation paramétrique locale \(f\) en \(0\) telle que pour un certain \((x,y)\mapsto g(x,y)\) on ait \(f(x,y)=(x,y,g(x,y))\) (ceci s’étend évidemment en tout point \(\neq 0\) de \(S\) et pour tout plan tangent - on préfère translater et tourner la surface pour se ramener à ce cas plus « visuel »). Avec \(Q\) la forme quadratique qui a mêmes dérivées premières et secondes que \(g\), on a alors nécessairement \(Q(x,y)=rx^2+ty^2+2sxy\) pour certains \(r\), \(t\), \(s\) (notation de Monge). On dit que \(0\) est:
Un point elliptique si \(rt>s^2\), \(Q\) est alors soit définie positive soit définie négative. Localement, la surface est entièrement d’un même côté du plan \(z=0\), et seul le point \(0\) est intersection du plan et de la surface (attention: localement).
Un point hyperbolique si \(rt<s^2\). La surface passe, localement, des deux côtés du plan tangent.
Un point parabolique si \(rt=s^2\) et \((r,s,t)\neq (0,0,0)\).
Un point plat si \(r=s=t=0\).
La quantité \(rt-s^2\) est appelée courbure de Gauss ou courbure totale de la surface \(S\) en \(0\).
Cette définition équivaut à l’intégrale \[Aire(S)=\int_{\Omega} {\parallel}\frac{\partial f}{\partial x} \wedge \frac{\partial f}{\partial y}{\parallel}\mbox{ (norme du produit vectoriel)}\]
Avec l’une ou l’autre de ces définitions, on peut montrer (laissé en exercice au lecteur) que l’aire est invariante par changement de variable, i.e. en remplaçant \(f\) par \(f\circ\varphi\) et \(\Omega\) par \(\Omega'\), où \(\varphi\) : \(\Omega'\to\Omega\) est un \({\cal C}^1\)-difféomorphisme.
- 1 Au profit de l’équivalent obtenu en remplaçant \(...243999999999...\) par \(...2440000...\).
- 2 Il s’agit d’un élément de \({\cal L}(\mathbb{R}^p,\mathbb{R}^n)\).
- 3 Il s’agit d’un élément de \({\cal L}(\mathbb{R}^p,\mathbb{R}^n)\).
- 4 On « recolle » ainsi un élément de \(\mathbb{R}^p\) et un élément de \(\mathbb{R}^{n-p}\) pour obtenir un élément de \(\mathbb{R}^n\).
Bibliographie
- [CAR] H. Cartan, Calcul différentiel, Hermann, 1977.[CF3] A. Chambert-Loir, S. Fermigier, Exercices de mathématiques pour l’agrégation, Analyse 3, Masson, 1996.[LAN] S. Lang, Real analysis, Addison-Wesley Publishing company, 1969.[VP] J. Vauthier, J.J. Prat, Cours d’analyse mathématiques de l’intégration, Masson, 1994.
Barre utilisateur
[ID: 21] [Date de publication: 12 mars 2021 17:09] [Catégorie(s): Le cours d'agrégation ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 5 ] [Auteur(s): Christophe Antonini Olivier Teytaud Pierre Borgnat Annie Chateau Edouard Lebeau ]
Commentaires sur le cours
Documents à télécharger
L'article complet
Continuer à lire

Produit de convolution

Combinatoire et dénombrements

Dénombrements et probabilités

Quelques résultats supplémentaires de théorie des nombres

Géométrie affine et projective

Géométrie projective

Zoologie de la géométrie

Fonctions holomorphes

Statistique

Analyse fonctionnelle

Quelques résultats inclassables

Analyse numérique et mathématiques appliquées

Théorie des ensembles – autres systèmes axiomatiques – construction des ensembles usuels

Topologie

Espaces \({\cal L}^p\) et espaces \(L^p\)

Développements limités et comparaison de fonctions

Approximation de fonctions

Extrema

Formes différentielles

Théorie des groupes

Anneaux et corps

Corps

Algèbre linéaire

Algèbre multilinéaire

Espaces préhilbertiens et espaces de Hilbert

Algèbre linéaire en dimension finie

Intégration

Réduction des endomorphismes

Quelques synthèses et compléments d’analyse

Interversions

Séries entières et fonctions holomorphes

Polynômes

Fourier

Graphes

Ensembles ordonnés