Conseils

Quelques conseils fondamentaux pour la préparation des concours.

Conseils d’oral

Vous préparez des épreuves orales des concours. Eh, oui, dès cette année !

Il n’est pas trop tôt pour prendre des bonnes habitudes. Vous passez bien des colles dès cette année, non ?
Les << petites >> mines ne sont pas des écoles méprisables.
Les conseils qui vont suivre vont vous permettre de mieux vivre vos colles.

L’interrogateur est là pour vous évaluer. Comme à l’écrit vous devez le convaincre de vous donner la meilleure note possible. Vous devez communiquer avec lui. Il faut savoir que plus de la moitié de la communication est non verbale.

Il faut éviter :

de regarder ses chaussures en attendant que ça se passe. C’est à vous de commencer l’interrogation. Vous devez donner une idée (bonne ou mauvaise) à laquelle l’interrogateur pourra se raccrocher.
dans le même ordre d’idée, de griffonner des hiéroglyphes minuscules que vous effacerez nerveusement à la première question de l’interrogateur.
de bluffer. N’oubliez jamais que vous êtes un amateur en face d’un professionnel. Le bluff, fortement déconseillé à l’écrit, est mortel à l’oral et à tous les coups. Il vaut mieux dire << je ne sais pas >> y compris à une question de cours que d’essayer d’enfumer l’interrogateur.
de venir à l’oral sans avoir lu les rapports des années précédentes. Ceci vaut à l’écrit mais est particulièrement important à l’oral. Chaque phrase est pesée et vous devez deviner les situations qu’elle peut décrire. Si votre interrogateur a rédigé le rapport de l’année précédente, venir sans le lire équivaut à un sacrifice rituel.
d’avoir une notion floue des propriétés du cours. << Il faut aussi prendre conscience que des questions de cours peuvent être abordées lors de l’oral >> (rapport de concours).
d’utiliser des propriétés hors-programme. Un candidat qui citerait un théorème hors-programme et difficile puis qui se ferait coincer sur une question de cours élémentaire (déjà vu) serait discrédité.

Il faut au contraire :

S’efforcer de faire un dessin, si possible en rapport avec la question. L’interrogateur pourra s’en servir pour vous guider. Une colle = un dessin parait un slogan réaliste.
Donner la possibilité à l’interrogateur de vous aider. Par exemple prendre des particuliers. Donner une solution partielle, par exemple en renforçant les hypothèses, n’est pas méprisable.

Comme il est signalé plus haut, la communication est aussi non verbale. La communication passera moins bien si vous affichez une mine renfrognée. En caricaturant (à peine) il y a trois types de candidats :

les brillants qui quoi qu’ils fassent auront une note brillante.
ceux qui auront beau se débattre, feront une piètre prestation.
l’énorme majorité va se débrouiller tant bien que mal face aux questions posées. Ceux-là ne dominent pas leur sujet et l’interrogateur le voit bien. Pour eux sourire peut faire la différence entre être admis ou pas.

Heureux comme une rivière
qui peut suivre son cours
sans sortir de son lit. Graffiti anonyme en salle de classe. XX\(^e\) siècle.

Conseils d’étude

Attitude pendant le cours

Il est très important d’être parfaitement concentré pendant les heures de cours. Ne jamais vous dire que si vous ne comprenez pas quelque chose sur le moment, vous aurez le loisir de reprendre ce point chez vous. Un quart d’heure d’inattention vous prendra plus d’une heure à rattraper et vous n’aurez matériellement pas le temps de combler ces lacunes plus tard. Il est donc important de se présenter au cours en bonne condition; pour cela il est indispensable d’adopter un rythme de vie équilibré et en particulier de bien dormir pour arriver en cours parfaitement reposé.

En ce qui concerne la prise de notes, tout dépend de votre faculté à écrire rapidement. Votre professeur doit boucler un programme très chargé, et par moments il est obligé d’accélérer. Le plus important est de comprendre l’essentiel pendant le cours, quitte à ne pas tout écrire. Notez précisément les définitions et les énoncés des théorèmes, mais ne notez pas les phrases complètes pendant le cours, utilisez des abréviations. Il faut être en permanence attentif à ce que dit votre professeur et comprendre les idées qu’il exprime, quitte à ne pas tout noter.

Après chaque cours le soir, faites une synthèse de ce que vous avez vu pendant la journée en mettant en évidence les points importants. Vous devez vous présenter au cours suivant en ayant en tête les définitions du cours précédent. Le moindre retard dans votre travail peut avoir des répercussions importantes par la suite.

Bien comprendre les définitions et les hypothèses de théorèmes

Les définitions ainsi que les théorèmes du cours sont très importants, vous aurez à les utiliser pendant les devoirs et elles vous serviront à comprendre la suite du cours. Une erreur fréquente consiste à vouloir aller trop vite lors des révisions en ne se contentant que d’une connaissance superficielle. Il est normal de passer du temps à bien réfléchir aux définitions et aux hypothèses des théorèmes. En particulier, prenez l’habitude de chercher vos propres exemples, contre-exemples et de faire le maximum de schémas pour vous imprégner de ces connaissances fondamentales.

Prenons l’exemple du théorème des accroissements finis :

(Accroissements finis).

Soit \(f : [a, b] \mapsto \mathbb{R}\) une fonction vérifiant les hypothèses :

\(f\) est continue sur le segment \([a,b]\),
\(f\) est dérivable sur \(]a, b[\),

Alors il existe \(c \in ]a, b[\) tel que \(f(b) - f(a) = (b-a) f'(c)\).

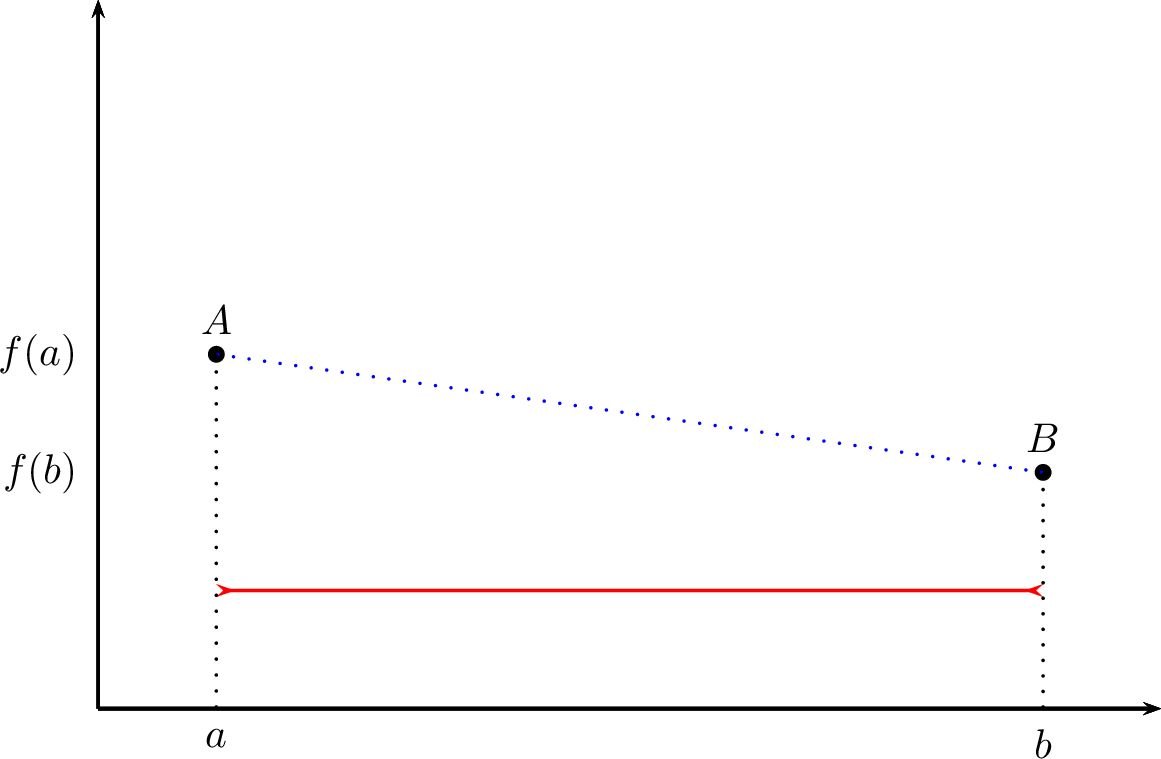
Pour comprendre ce théorème, essayons de visualiser le résultat. On peut écrire \(\dfrac{f(b)-f(a)}{b-a} = f'(c)\). Le quotient \(\dfrac{f(b)-f(a)}{b-a}\) représente la pente de la corde joignant les points \(A=(a,f(a))\) et \(B=(b,f(b))\). Le réel \(f'(c)\) représente la pente de la tangente à la courbe \(y=f(x)\) au point \(C=(c,f(c))\). Si l’on place une règle joignant les points \(A\) et \(B\) et qu’on déplace cette règle en maintenant sa pente, on va rencontrer au moins une tangente à la courbe. On voit sur notre dessin que le \(c\) du théorème n’est pas nécessairement unique.

Réfléchissons aux hypothèses du théorème. Pour parler de \(f'(c)\) où \(c \in ]a,b[\), il faut supposer que \(f\) est dérivable sur \(]a, b[\). Si l’on suppose uniquement que \(f\) est continue sur \(]a, b[\), le résultat peut être faux comme le montre le contre-exemple suivant :

La conclusion du théorème dit qu’il existe un réel \(c\) intérieur au segment \([a,b]\). Le fait que \(c\neq a\) et \(c\neq b\) est important dans les applications. On peut se demander si ce théorème reste valable lorsque la fonction est à valeurs complexes. La réponse est négative. Si l’on considère la fonction \(f : \left\{ \begin{array}{ccl} [0,2\pi] & \longrightarrow & \mathbb{C} \newline x & \longmapsto & e^{ix} \end{array} \right.\), on a bien \(f\) qui est continue sur \([0, 2\pi]\), \(f\) dérivable sur \(]0, 2\pi[\) mais \(f(1)-f(0) = 0\) et pour tout \(c \in ]0, 2\pi[\), \(f'(c) = ie^{ic} \neq 0\).

Faire une synthèse des points importants d’une démonstration

Prenez l’habitude de résumer les points importants d’une démonstration en quelques phrases et schémas. C’est ainsi que vous les retiendrez sur le long terme. Prenons l’exemple du théorème des accroissements finis. Si l’on observe le schéma précédent, on s’aperçoit que le point \(C\) rend extrémale la hauteur entre la courbe et la corde \([AB]\) ce qui nous conduit à introduire une bonne fonction auxiliaire.

L’équation de la corde s’écrit \(y = f(a) + (x-a) \dfrac{f(b)-f(a)}{b-a}\) d’où la fonction auxiliaire définie par \[\varphi(x) = f(x) - f(a) - (x-a)\dfrac{f(b)-f(a)}{b-a}\] On a \(f(b) = f(a) = 0\) et il suffit d’appliquer le théorème de Rolle (en vérifiant les hypothèses) à cette fonction auxiliaire.

Sur une fiche, vous pouvez résumer les idées de cette démonstration :

Introduire la fonction auxiliaire et faire le dessin ci-dessus.
Vérifier les hypothèses de Rolle pour cette fonction auxiliaire.
En déduire qu’elle admet un extremum.

Prenons un autre exemple typique, le théorème du rang :

Soit \(u : E \mapsto F\) une application linéaire entre deux espaces vectoriels avec \(E\) de dimension finie. On a la formule du rang : \[\dim E = \dim(\operatorname{Ker}u) + \mathop{\mathrm{rg}}(u)\]

On résume la démonstration avec les points suivants :

Vérifier que \(\mathop{\mathrm{Im}}u\) est isomorphe à tout supplémentaire \(V\) de \(\operatorname{Ker}u\).
Pour vérifier cet isomorphisme, considérer la restriction \(v\) de \(u\) à \(V\).
Vérifier que \(v\) est surjective en décomposant un antécédent d’un vecteur \(y \in \mathop{\mathrm{Im}}u\) sur \(\operatorname{Ker}u\) et \(V\) :

Les-mathematiques.net
Utiliser que \(\dim V = \dim \mathop{\mathrm{Im}}u\) et que \(\dim E = \dim \operatorname{Ker}u + \dim V\).

Conseils de rédaction

Vous préparez des épreuves écrites de concours. Contrairement au baccalauréat, les examinateurs n’ont pas de consignes d’indulgence pour vous attribuer artificiellement des points, mais leur but est de vous classer par rapport aux autres candidats. Si vous rendez une copie mal rédigée, illisible où il manque des arguments essentiels, ou au contraire, si vous utilisez trois pages pour un calcul qui ne nécessite que deux lignes, vous serez inévitablement pénalisé. Il est très important de s’entraîner pendant les deux années de préparation à rédiger de façon correcte vos devoirs pour prendre de bonnes habitudes et être bien préparé pour les concours. Voici quelques mauvaises habitudes à perdre :

Écrire directement sur votre copie la première idée qui vous passe par la tête (quelquefois au crayon de papier …)
Commencer une phrase ou une démonstration et s’arrêter en plein milieu ! Au lieu de montrer votre inconsistance au correcteur (n’espérez pas gagner quelques centièmes de points ainsi), mieux vaut ne rien écrire.
Effectuer un calcul directement sur votre copie en détaillant toutes les étapes de façon maladroite.
Sauter une question dont vous ne trouvez pas la solution immédiatement, quitte à y revenir ensuite en écrivant dans la marge, en mettant une astérisque demandant au correcteur de se reporter à la dernière page …
Utiliser des formules de type c’est évident , trivialement …
Citer vaguement un théorème : d’après un théorème sans vérifier ses hypothèses d’application.
Écrire de façon très compacte sans jamais passer à la ligne. Les quelques centimes d’euros que vous économisez en feuilles n’intéresseront certainement pas votre correcteur qui tient à sa vue !
Écrire trop gros en utilisant quelques dizaines de feuilles doubles pour un problème qui n’en nécessite que deux.

Il faut au contraire :

Utiliser impérativement un brouillon sur lequel vous pouvez chercher les idées de démonstrations, faire des calculs longs …C’est uniquement une fois que vous avez les idées claires sur la façon de procéder que vous rédigez au propre le calcul ou la démonstration.
Si vous vous apercevez que vous avez fait une erreur, n’utilisez pas l’effaceur ni le blanco (perte de temps et souvent illisible), mais barrez proprement ce que vous avez écrit et recommencez.
Une fois que vous avez trouvé une idée de preuve, prenez le temps de vous demander s’il n’y a pas moyen de la simplifier encore. Repérez les points importants qu’il faudra mettre en évidence au propre, ainsi que les détails que vous pourrez minimiser dans la rédaction définitive. Faites de même pour un calcul, ne recopiez pas toutes les étapes, mais uniquement les plus importantes.
Encadrez les résultats de calculs demandés.
Ne cherchez pas à grappiller des points, mais traitez les questions les unes après les autres en passant un minimum de temps à chaque question. Ce temps n’est jamais perdu car vous aurez mieux assimilé l’énoncé, repéré que le résultat peut servir par la suite et vous serez moins bloqué sur les questions suivantes.
Numérotez correctement les questions que vous traitez en laissant un espace blanc si vous n’avez pas trouvé le résultat. Vous pourrez compléter cet espace par la suite et le correcteur suivra votre copie selon l’ordre du problème.
Pour rédiger une démonstration ou un calcul, passez souvent à la ligne, centrez des formules …Le but est de mettre en évidence les points importants et de montrer à votre correcteur que vous les avez vus.
Tirez un trait horizontal pour séparer chaque question, vous facilitez ainsi la lecture de votre copie.
Si vous devez utiliser un résultat précédent du problème, citez précisément le numéro de la question où ce résultat a été démontré. De même, respectez scrupuleusement les notations de l’énoncé.
Si vous utilisez un théorème du cours, citez-le précisément (il a souvent un nom), et surtout vérifiez ses hypothèses précises avant de l’appliquer (vous montrez ainsi que vous connaissez votre cours).
Évitez trop de phrases longues et verbeuses, allez à l’essentiel. Au contraire, une copie avec uniquement des formules est illisible. Il faut savoir trouver le juste milieu. N’abusez pas des abréviations et essayez de rédiger des phrases simples mais correctes.
N’utilisez jamais les symboles \(\Rightarrow\), \(\Longleftrightarrow\) dans vos démonstrations, mais des mots comme donc , par conséquent …

Si on vous demande une démonstration, commencez par travailler au brouillon :

Bien analyser l’énoncé pour comprendre ce que vous devez montrer. Demandez-vous la nature de chaque objet manipulé (vecteur, application …).
Écrire le plan de démonstration au brouillon.
Chercher un brouillon l’idée de la démonstration. Pour cela,
- Essayez de voir un lien entre le résultat à démontrer et un point du cours ou une question précédente du problème.
- Faites éventuellement des schémas pour trouver l’idée.
- N’hésitez pas à chercher un exemple ou à traiter la question dans un cas plus simple, ou à faire des hypothèses supplémentaires.
Demandez-vous dans quel ordre vous devez introduire les objets nécessaires.

Une fois que vous pensez que vous avez bien compris l’idée, vous pouvez rédiger au propre :

Commencez par citer le résultat que vous allez démontrer.
Si vous voulez montrer une équivalence ou une égalité d’ensembles, procédez systématiquement par double implication ou double inclusion.
Rédigez la démonstration en respectant le plan.
Mettez en évidence les points importants (en soulignant, en passant à la ligne …).
Une fois votre preuve rédigée, relisez-la en vous assurant que chaque objet est bien introduit et que le plan a été respecté.
Si un schéma n’est pas suffisant à lui seul, il peut illustrer votre démonstration. N’hésitez pas à le reproduire sur votre copie.

Bibliographie

Barre utilisateur

[ID: 81] [Date de publication: 5 janvier 2022 23:16] [Catégorie(s): Le cours de SUP ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]