Lecture zen
Introduction au groupe orthogonal
Espaces préhilbertien
Introduction au groupe
orthogonal
Dans tout ce chapitre, \(E\) désigne un \(\mathbb{R}\)-espace vectoriel.
Pour bien aborder ce chapitre
On va généraliser dans ce chapitre la notion de produit scalaire étudiée dans les chapitres [geom_plan] et [geom_espace] aux espaces vectoriels. Cela permettra d’étendre la notion de vecteurs orthogonaux et les notions afférentes (norme, base orthonormale, théorème de Pythagore, projections et symétries orthogonales...) à certains espaces vectoriels de fonctions ou de matrices par exemple. Un des prolongements importants de ce chapitre sera celui consacré aux séries de Fourier en seconde année et qui formera un magnifique exemple d’illustration de la puissance de l’algèbre mise au service de l’analyse.
Nous étudierons dans la seconde moitié de ce chapitre les endomorphismes d’un espace euclidien qui préservent le produit scalaire, ou autrement dit les isométries. Nous verrons que les isométries d’un espace euclidien \(E\) donné forment un groupe appelé groupe orthogonal et nous étudierons complètement ce groupe dans le cas où \(E=\mathbb{R}^2\) et \(E=\mathbb{R}^3\). Nous ferons le lien entre les matrices et ces endomorphismes remarquables et nous introduirons la notion de matrice orthogonale.
Définitions et règles de calcul
Produit scalaire
(Produit scalaire). Soit \(E\) un \(\mathbb{R}\)-espace vectoriel. On appelle
produit scalaire sur \(E\),
une application : \(\varphi: E\times E
\rightarrow \mathbb{R}\) vérifiant :
\(\varphi\) est une forme bilinéaire : \(\forall (x,y,z)\in E^3, \forall (\lambda,\mu)\in \mathbb{R}^{2}\) \[\begin{aligned} \varphi(\lambda x +\mu y, z) &= \lambda \varphi(x,z) + \mu \varphi(y,z) ,\newline \varphi(x,\lambda y + \mu z ) & = \lambda \varphi(x,y) + \mu \varphi(y,z). \end{aligned}\]
\(\varphi\) est symétrique : \[\forall (x,y)\in E^2, \quad\varphi(x,y)= \varphi(y,x).\]
\(\varphi\) est définie : \[\forall x\in E, \quad(\varphi(x,x)=0)\Longleftrightarrow (x=0).\]
\(\varphi\) est positive : \[\forall x \in E, \quad\varphi(x,x)\geqslant 0.\]
On note \(\left( x \mid y \right) = \varphi(x, y)\)
le produit scalaire. En géométrie, on utilise également la notation
\(\overrightarrow{x} .
\overrightarrow{y}\).
(Espace préhilbertien, Espace
euclidien). Un \(\mathbb{R}\)-espace vectoriel \(E\) muni d’un produit scalaire est appelé
un espace préhilbertien réel. Si de plus \(E\) est de dimension finie, on dit que
\(E\) est un espace
euclidien.
Norme
Dans toute la suite, on considère un préhilbertien réel \(\left(E,\left( \cdot \mid \cdot \right)\right)\).
(Norme euclidienne associée à un produit
scalaire). On définit la norme euclidienne associée à un
produit scalaire \(\left( \cdot \mid \cdot
\right)\) par :
\[\forall x\in E, \quad \boxed{ \left\| x
\right\| = \sqrt{ \left( x \mid x \right) } }.\]
\(\left\|\cdot\right\|\) est bien définie car
\(\left( \cdot \mid \cdot \right)\) est
une forme bilinéaire positive et donc pour tout vecteur \(x\in E\), \(\left( x \mid x \right)\geqslant 0\).
(Règles de calcul).
Pour tous vecteurs \(x, y \in E\), et tout réel \(\lambda \in \mathbb{R}\) :
\[\left( \sum_{i=1}^n \lambda_i x_i \mid
\sum_{j=1}^m \mu_j y_j \right) = \sum_{i=1}^n
\sum_{j=1}^m \lambda_i \mu_j \left( x_i \mid y_j \right),\]
\[\Bigl\| \sum_{i=1}^n \lambda_i x_i
\Bigr\|^2 = \sum_{i=1}^n
\lambda_i^2 \lVert x_i \rVert_{ }^2 + 2\sum_{1\leqslant i < j
\leqslant n} \lambda_i
\lambda_j \left( x_i \mid x_j \right) .\]
\(\lVert \lambda . x \rVert_{ } = \lvert \lambda \rvert ~ \lVert x \rVert_{ }\) ;
\(\lVert x+y \rVert_{ }^2=\lVert x \rVert_{ }^2 + 2\left( x \mid y \right) + \lVert y \rVert_{ }^2\) ;
\(\lVert x-y \rVert_{ }^2 = \lVert x \rVert_{ }^2 - 2\left( x \mid y \right) + \lVert y \rVert_{ }^2\) ;
\(\lVert x+y \rVert_{ }^2 + \lVert x-y \rVert_{ }^2 = 2(\lVert x \rVert_{ }^2 + \lVert y \rVert_{ }^2)\)
(égalité du parallélogramme) ;
\(\left( x \mid y \right) = \dfrac{1}{4}\left(\lVert x+y \rVert_{ }^2 - \lVert x-y \rVert_{ }^2\right)\) (identité de polarisation).
Pour des vecteurs \(x_1,\dots,x_n, y_1,\dots,y_m \in E\) et des scalaires \(\lambda_1,\dots,\lambda_n,\mu_1,\dots,\mu_m \in \mathbb{R}\),
Soient \(x,
y \in E\) et \(\lambda \in
\mathbb{R}\). En utilisant le fait que \(\left( \cdot \mid \cdot \right)\) est une
forme bilinéaire symétrique :
Les deux dernières formules sont conséquence de la bilinéarité du
produit scalaire.
\(\left\|\lambda x\right\|=\sqrt{\left( \lambda x \mid \lambda x \right)}=\sqrt{\lambda^2 \left( x \mid x \right)}=\left|\lambda\right| \left\|x\right\|\).
\(\lVert x+y \rVert_{ }^2=\left( x+y \mid x+y \right)=\left( x \mid x \right)+2\left( x \mid y \right) +\left( y \mid y \right)=\lVert x \rVert_{ }^2 + 2\left( x \mid y \right) + \lVert y \rVert_{ }^2\).
\(\lVert x-y \rVert_{ }^2 =\left( x-y \mid x-y \right)=\left( x \mid x \right)-2\left( x \mid y \right) +\left( y \mid y \right)= \lVert x \rVert_{ }^2 - 2\left( x \mid y \right) + \lVert y \rVert_{ }^2\) ;
En additionnant les deux égalités précédentes, on obtient l’égalité du parallélogramme.
Enfin, par soustraction de ces deux mêmes égalités, on obtient l’identité de polarisation.
(Inégalité de Cauchy-Schwarz).
Pour tous vecteurs \(x,y\in E\), on a l’inégalité de
Cauchy-Schwarz \[\boxed{\left| \left( x
\mid y \right) \right| \leqslant\lVert x \rVert_{ }\lVert y \rVert_{ }
}\] et on a égalité si et seulement si les deux vecteurs sont
colinéaires : \(\left| \left( x \mid y \right)
\right| = \lVert x \rVert_{ }\lVert y \rVert_{ }
\Longleftrightarrow\exists \lambda \in \mathbb{R} :\quad
(y=\lambda x \quad \textrm{ ou} \quad x = \lambda y)\).
Soient \(x,y\in E\). Pour tout \(\lambda\in\mathbb{R}\) , considérons :
\[P\left(\lambda\right)=\left( x+\lambda y
\mid x+\lambda y \right).\] D’après les règles de calcul
précédentes, on obtient \[P\left(\lambda\right)=\left( y \mid y
\right)\lambda^2+2\left( x \mid y \right)\lambda+\left( x \mid x
\right)=\left\|y\right\|^2
\lambda^2 + 2\lambda\left( x \mid y \right)+ \left\|x\right\|^2\]
et \(P\) est un trinôme du second degré
en \(\lambda\). Par ailleurs \(\forall
\lambda\in\mathbb{R},\quad P\left(\lambda\right)\geqslant 0\).
Donc \(P\) admet au plus une racine
réel et son discriminant réduit est négatif ou nul, ce qui s’écrit :
\(\left(\left( x \mid y
\right)\right)^2-\left\|y\right\|^2 \left\|x\right\|^2\leqslant
0\), c’est-à-dire \(\left|
\left( x \mid y \right) \right| \leqslant\lVert x \rVert_{ }~\lVert y
\rVert_{ }\). Si \(x\) et \(y\) sont colinéaires, on vérifie facilement
que \(\left| \left( x \mid y \right) \right| =
\lVert x \rVert_{ }\lVert y \rVert_{ }\). Réciproquement, si
cette égalité est vraie, alors le discriminant de \(P\) est nul et donc \(P\) admet une racine double \(\lambda_0\in\mathbb{R}\). On a donc \(\left( x+\lambda_0 y \mid x+\lambda_0 y
\right)=0\) ce qui n’est possible que si \(x+\lambda_0 y=0\) c’est-à-dire que si \(x=\lambda_0 y\).
(Inégalité de
Minkowski). Pour tous vecteurs
\(x,y\in E\), on a l’inégalité de
Minkowski \[\boxed{\Bigl|\lVert x
\rVert_{ } - \lVert y \rVert_{ } \Bigr| \leqslant
\lVert x+y \rVert_{ } \leqslant\lVert x \rVert_{ } + \lVert y
\rVert_{ } }\] et on a égalité dans la majoration de droite si et
seulement si les deux vecteurs \(x\) et
\(y\) se trouvent sur une même
demi-droite issue de l’origine : \(\exists
\lambda \geqslant 0:\quad y=\lambda
x\).
Soient \(x,y \in E\).
On applique les régles de calcul avec le produit scalaire [regles_calcul_prod_scalaire] et l’inégalité de Cauchy-Schwarz [Cauchy-Schwarz] : \[\begin{aligned} \left\|x+y\right\|^2 &=& \left\|x\right\|^2 +2 \left( x \mid y \right)+\left\|y\right\|^2 \\ &\leqslant& \left\|x\right\|^2 +2 \left\|x\right\|\left\|y\right\|+\left\|y\right\|^2 \newline &\leqslant& \left(\left\|x\right\|+\left\|y\right\|\right)^2\end{aligned}\] On a donc : \(\left\|x+y\right\|\leqslant\left\|x\right\|+\left\|y\right\|\).
Si \(x\) et \(y\) se trouvent sur une même demi-droite issue de l’origine, on vérifie facilement que cette dernière inégalité est une égalité. Réciproquement, supposons que \(\left\|x+y\right\|= \left\|x\right\|+\left\|y\right\|\). Alors, en reprenant le calcul précédent, on obtient \(\left( x \mid y \right)=\left\|x\right\|\left\|y\right\|\) et on est dans le cas d’égalité de la la formule de Cauchy-Schwarz. Donc \(x\) et \(y\) sont colinéaires : \(\exists\alpha\in\mathbb{R},\quad y=\alpha x\). On injecte cette égalité dans celle de départ, on trouve \(\left(1+\alpha\right)x=\left\|x\right\|+\left\|\alpha x\right\|\), c’est-à-dire : \(\left(1+\alpha \right){x} = \left(1+\left|\alpha\right|\right)\left\|x\right\|\). Si le vecteur \(x\) est nul alors il en est de même de \(y\) et la propriété est prouvée. Si \(x\) est non nul alors \(\alpha=\left|\alpha\right|\) et \(\alpha\) est bien positif.
Par ailleurs : \[\left\|x\right\|=\left\|x-y+y\right\|\leqslant \left\|x-y\right\|+\left\|y\right\|\] et \[\left\|y\right\|=\left\|y-x+x\right\|\leqslant\left\|y-x\right\|+\left\|x\right\|\] et comme \(\left\|y-x\right\|=\left\|x-y\right\|\), on obtient : \(\left\|x-y\right\|\geqslant \left\|x\right\|-\left\|y\right\|\) et \(\left\|x-y\right\|\geqslant\left\|y\right\|-\left\|x\right\|\), ce qui s’écrit aussi : \(\left\|x-y\right\|\geqslant\Bigl|\left\|x\right\|-\left\|y\right\|\Bigr|\).
De manière plus générale :
(Norme).
On appelle norme sur \(E\) une
application : \(\left\|\cdot\right\|:E\rightarrow
\mathbb{R}\) vérifiant :
\(\forall x\in E,\quad \left\|x\right\|=0 \Rightarrow x=0\).
\(\forall x\in E,\quad \forall \lambda \in \mathbb{R},\quad \left\|\lambda x\right\|=\left|\lambda\right|\left\|x\right\|\).
\(\forall x,y\in E,\quad \left\|x+y\right\|\leqslant\left\|x\right\|+\left\|y\right\|\) (Inégalité triangulaire).
(Norme associée au produit scalaire).
La norme euclidienne \(\left\|\cdot\right\|\) associée à un
produit scalaire \(\left( \cdot \mid \cdot
\right)\) sur \(E\) est une
norme sur \(E\).
Les propriétés \(2\) et \(3\) ont déjà été prouvées dans les
théorèmes [regles_calcul_prod_scalaire] et
[Inegalite_de_minkowski]. Démontrons la première. Soit \(x\in E\) tel que \(\left\|x\right\|=0\) alors \(\left( x \mid x \right)=0\) mais comme
\(\left( \cdot \mid \cdot \right)\) est
une forme bilinéaire définie, \(x=0\).
Quelques exemples de produits
scalaires et leur norme associée (à retenir) :
Produit scalaire usuel sur \(\mathbb{R}^{n}\) : Si \(X=(x_1,\dots,x_n), Y=(y_1,\dots, y_n)\in \mathbb{R}^{n}\), \[\left( X \mid Y \right) = x_1 y_1+\dots x_n y_n = \sum_{i=1}^n x_i y_i ,\] \[\lVert X \rVert_{ } = \sqrt{ x_1^2+\dots + x_n^2} = \sqrt{ \sum_{i=1}^n x_i^2} .\]
Sur l’espace des fonctions continues sur \([a,b]\), \(E=\mathcal{C}([a,b],\mathbb{R} )\), \(f,g\in E\) : \[\left( f \mid g \right) = \int_a^b f(t)g(t) dt ,\] \[\lVert f \rVert_{ } = \sqrt{ \int_a^b \left(f(t)\right)^2 dt } .\]
Sur l’espace des fonctions \(f : \mathbb{R} \mapsto \mathbb{R}\) continues et \(2\pi\)-périodiques, \(E=\mathcal{C}_{2\pi}(\mathbb{R} )\), \(f,g\in E\) : \[\left( f \mid g \right) = \int_0^{2\pi} f(t)g(t) dt ,\] \[\lVert f \rVert_{ } = \sqrt{ \int_0^{2\pi} \left(f(t)\right)^2 dt } .\]
Sur l’espace des matrices carrées \(\mathfrak{M}_{n}(\mathbb{R})\), \(A,B\in \mathfrak{M}_{n}(\mathbb{R})\) \[= \mathop{\mathrm{Tr}}(A{B}^{\mathrm{T}}),\] \[\left\| A \right\| = \sqrt{ <A,A> }= \sqrt{\mathop{\mathrm{Tr}}(A{A}^{\mathrm{T}}) }.\] Voir l’exercice [exo_tr_produit_scalaire] page [exo_tr_produit_scalaire].
(Vecteur unitaire). Soit \(x\) un vecteur d’un \(\mathbb{R}\)-espace vectoriel \(E\) muni d’une norme \(\left\|\cdot\right\|\). On dit que \(x\) est unitaire si et seulement
si \(\left\|x\right\|=1\).
Orthogonalité
On considère dans ce paragraphe un espace préhilbertien réel \((E,\left( . \mid . \right))\).
(Vecteurs orthogonaux). Deux vecteurs
\(x\) et \(y\) de \(E\) sont dits orthogonaux lorsque
\(\left( x \mid y \right)=0\).
(Identité de
Pythagore). Soient \(x\) et \(y\) deux vecteurs de \(E\). Alors \[\left( x \mid y \right) = 0 \Longleftrightarrow
\lVert x+y \rVert_{ }^2 = \lVert x \rVert_{ }^2 +\lVert y \rVert_{
}^2.\]
D’après la formule
[regles_calcul_prod_scalaire] : \[\left\|x+y\right\|^2=\left\|x\right\|^2+2\left( x
\mid y \right)+\left\|y\right\|^2,\] et il vient immédiatement :
\[\begin{aligned}
\left( x \mid y \right) = 0
\Longleftrightarrow\lVert x+y \rVert_{ }^2 = \lVert x \rVert_{ }^2
+\lVert y \rVert_{ }^2.\end{aligned}\]
( Des vecteurs orthogonaux \(2\) à \(2\) forment un système libre).
Soit \(S=(x_1,\dots,x_n)\) une famille de vecteurs
non-nuls deux à deux orthogonaux : \[\forall
(i,j)\in [\kern-0.127em[ 1, n ]\kern-0.127em]^2,
\quad i\neq j \Rightarrow \left( x_i \mid x_j \right)=0 .\]
Alors la famille \(S\) est libre.
Soient \(\alpha_1,\dots,\alpha_n\in\mathbb{R}\) tels
que \(\alpha_1 x_1+\dots+\alpha_n
x_n=0\). Soit \(i\in\llbracket
1,n\rrbracket\). Du fait de la bilinéarité du produit scalaire et
que les vecteurs de cette famille sont deux à deux orthogonaux : \[0=\left( x_i \mid \sum_{j=1}^n \alpha_i x_i
\right) = \sum_{j=1}^n \alpha_i
\left( x_i \mid x_j \right) = \alpha_i\left( x_i \mid x_i
\right)\] Comme \(x_i\neq 0\),
\(\left( x_i \mid x_i \right)\neq 0\)
et il vient que \(\alpha_i=0\). Cette
égalité est vraie pour tout \(i\in\llbracket
1,n\rrbracket\). On montre ainsi que la famille \(S\) est libre.
(Sous-espaces orthogonaux). Soient
\(F\) et \(G\) deux sous-espaces vectoriels de \(E\). On dit qu’ils sont orthogonaux si et
seulement si \[\forall x\in F, \forall y\in
G, \quad\left( x \mid y \right)=0.\]
(Orthogonal d’une partie). Soit \(A \subset E\) une partie de \(E\). On définit l’orthogonal de \(A\) comme étant le sous-ensemble de \(E\) noté \(A^{\perp}\) et donné par : \[A^{\perp}=\{ x\in E ~|~ \forall a\in A, \left( x
\mid a \right)=0 \}\]
(Propriétés de
l’orthogonal). Soient
\(A,B\subset E\) deux parties de \(E\).
\(A^{\perp}\) est un sous-espace vectoriel de \(E\).
\(A\subset B \Rightarrow B^{\perp} \subset A^{\perp}.\)
\(A^{\perp} = \left(\mathop{\mathrm{Vect}}(A)\right)^{\perp}.\)
\(A\subset \left(A^{\perp}\right)^{\perp}.\)
Le vecteur nul est orthogonal à tous les vecteurs de \(A\) donc \(0\in A^{\perp}\). Soient \(\alpha,\beta \in\mathbb{R}\), \(x,y\in A^{\perp}\) et \(a\in A\). Alors \(\left( \alpha x + \beta y \mid a \right)=\alpha\left( x \mid a \right)+\beta \left( y \mid a \right)=0\) donc \(\alpha x + \beta y \in A^{\perp}\). \(A^{\perp}\) est donc bien un sous-espace vectoriel de \(E\).
Supposons que \(A\subset B\). Soit \(x\in B^{\perp}\). Montrons que \(x\in A^{\perp}\). Soit \(a\in A\). Comme \(A\subset B\), \(a\in B\) et \(\left( x \mid a \right)=0\). Donc \(x\in A^{\perp}\).
On a \(A\subset \mathop{\mathrm{Vect}}\left(A\right)\) donc d’après la propriété précédente : \(\left(\mathop{\mathrm{Vect}}(A)\right)^{\perp} \subset A^{\perp}\). Réciproquement, si \(x\in A^{\perp}\) et si \(y\in Vect\left(A\right)\) montrons que \(\left( x \mid y \right)=0\). Il existe \(n\in \mathbb{N}^*\), \(\alpha_1,\dots,\alpha_n \in \mathbb{R}\) et \(a_1,\dots,a_n\in A\) tels que : \(y=\sum_{i=1}^n \alpha_i a_i\) et \[\left( x \mid y \right)=\sum_{i=1}^n \alpha_i\left( x \mid a_i \right)=0\] car \(x\in A^{\perp}\). Voilà qui termine la démonstration du troisième point.
Enfin, si \(a\in A\) et si \(x\in A^{\perp}\) alors \(\left( a \mid x \right)=0\) et donc \(a\in \left(A^{\perp}\right)^{\perp}\) ce qui prouve la dernière inclusion.
Espaces euclidiens
On considère dans toute la suite de ce chapitre un espace euclidien \(E\) muni d’un produit scalaire noté \(\left( . \mid . \right)\) et \(\lVert . \rVert_{ }\) la norme euclidienne associée. On note \(n\) la dimension de \(E\).
Bases orthogonales, orthonormales
(Bases orthogonales, orthonormales).
Soit \(e=(e_1,\dots,e_n)\) une base de
\(E\). On dit que \(e\) est une base
orthogonale si et seulement si ses vecteurs sont deux à deux orthogonaux, c’est-à-dire si et seulement si : \[\forall (i,j)\in [\kern-0.127em[ 1, n ]\kern-0.127em]^2,\quad i\neq j \Rightarrow \left( e_i \mid e_j \right)=0.\]
orthonormale si et seulement si ses vecteurs sont deux à deux orthogonaux et unitaires, c’est-à-dire si et seulement si : \[\forall(i,j)\in [\kern-0.127em[ 1, n ]\kern-0.127em]^2, \quad \left( e_i \mid e_j \right)=\delta_{ij}.\]
Si on se donne un système \(\left(e_1,\dots,e_n\right)\) de vecteurs
deux à deux orthogonaux d’un espace vectoriel euclidien de dimension
\(n\) alors d’après la proposition
[deux_a_deux_orthogonaux_implique_libre], ce système est libre.
Comme il est libre de rang maximal c’est une base (orthogonale) de \(E\).
La base canonique de \(\mathbb{R}^{n}\) est orthonormale pour le
produit scalaire usuel.
( Calculs dans une base
orthonormale). Soit
\(e=(e_1,\dots,e_n)\) une base
orthonormale de \(E\).
Les coordonnées d’un vecteur dans une base orthonormale sont données par les produits scalaires : \[\boxed{x = \sum_{i=1}^n \left( x \mid e_i \right) e_i}.\]
Si \(x=x_1e_1+\dots+x_ne_n\) et \(y=y_1e_1+\dots+y_ne_n\), alors \[\boxed{\left( x \mid y \right) = \sum_{i=1}^n x_i y_i = x_1y_1+\dots +x_ny_n} .\]
Si \(x=x_1e_1+\dots+x_ne_n\), \[\boxed{\lVert x \rVert_{ }^2 = \sum_{i=1}^n x_i^2 = x_1^2+\dots+x_n^2} .\]
Ces formules se prouvent facilement
en utilisant les règles de calcul avec le produit scalaire
[regles_calcul_prod_scalaire] et le fait que : \(\forall(i,j)\in [\kern-0.127em[ 1, n
]\kern-0.127em]^2, \quad \left( e_i \mid e_j
\right)=\delta_{ij}.\)
Procédé d’orthonormalisation de Schmidt
Erhard Schmidt, né le 13 janvier 1876 à Dorpat (Estonie), mort le 06 décembre 1959 à Berlin)
Mathématicien allemand. Il fait ses études, comme c’est souvent le cas à l’époque en Allemagne, dans différentes universités allemandes et les termine à Berlin. Il soutient sa thèse en 1905 sous la direction de David Hilbert. Elle porte sur les équations intégrales. Après avoir enseigné successivement dans les universités de Bonn, Zurich, Erlangen et Breslau, il est nommé en 1917 comme professeur à l’Université de Berlin où il occupe le poste laissé vacant par Schwarz. Dans les années 1930, il subit la montée du nazisme et alors que ses collègues juifs (Schur, von Mises) doivent quitter l’Université, il est sommé de prendre des résolutions contre les juifs. Il s’acquitte de cette tâche avec si peu de zèle que les nazis diront de lui à l’époque qu’il ne comprend pas le problème juifet qu’il ne sera pas critiqué par la suite. Erhard Schmidt est un des fondateurs de l’analyse fonctionnelle. Il a beaucoup contribué à la théorie des espaces de Hilbert que vous découvrirez en spé et a simplifié et généralisé un certain nombre de résultats d’Hilbert. C’est dans un article de 1907 sur les équations intégrales qu’il expose le procédé d’orthonormalisation. Notons que ce procédé avait été découvert au préalable par Laplace mais c’est Schmidt qui su en donner le premier un exposé clair.
(Théorème de Schmidt).
Soit \(E\) un espace euclidien de dimension \(n\) et \(e=(e_1,\dots,e_n)\) une base quelconque de
\(E\). Alors il existe une \(\varepsilon=(\varepsilon_1,\dots,\varepsilon_n)\)
de \(E\) vérifiant :
\(\forall i\in [\kern-0.127em[ 1, n ]\kern-0.127em], \quad \varepsilon_i \in \mathop{\mathrm{Vect}}(e_1,\dots,e_i)\) ;
\(\forall i\in [\kern-0.127em[ 1, n ]\kern-0.127em], \quad \left( e_i \mid \varepsilon_i \right) > 0\).
On va mettre en place un algorithme
permettant de construire la base \(\varepsilon\).
: Comme \(e\) est une base, \(e_1\) est non nul et le vecteur \(\varepsilon_1=\dfrac{e_1}{ \left\|e_1\right\|}\) est unitaire et vérifie \(Vect\left({\rm e}_1\right)= Vect\left(\varepsilon_1\right)\) ainsi que \(\left( e_1 \mid \varepsilon_1 \right)=\left\|e_1\right\|>0\).
Soit \(k\in \llbracket 1,n-1\rrbracket\). Supposons les vecteurs \(\varepsilon_1,\dots,\varepsilon_k\) construits tels que :
La famille \(\left(\varepsilon_1,\dots,\varepsilon_k\right)\) est orthonormale;
\(\forall i\in [\kern-0.127em[ 1, k ]\kern-0.127em], \quad \varepsilon_i \in \mathop{\mathrm{Vect}}(e_1,\dots,e_i)\) ;
\(\forall i\in [\kern-0.127em[ 1, k ]\kern-0.127em], \quad \left( e_i \mid \varepsilon_i \right) > 0\).
Construisons un vecteur \(\varepsilon_{k+1}\) répondant au problème. Les conditions qu’il doit remplir (voir la figure [fig:redressement_schmidt]) nous invitent à le chercher sous la forme \(\varepsilon_{k+1}=\alpha_1 \varepsilon_1+\dots+\alpha_k \varepsilon_k+ e_{k+1}\) où : \(\forall i\in\llbracket 1,k\rrbracket,\quad \alpha_i\in\mathbb{R}\). Pour tout \(i\in\llbracket 1,k\rrbracket\), on a la série d’équivalences : \[\begin{aligned} \varepsilon_{i} \perp \varepsilon_{k+1}&\Longleftrightarrow& \left( \varepsilon_{i} \mid \varepsilon_{k+1} \right)=0 \\ &\Longleftrightarrow& \sum_{j=1}^{k} \alpha_j\left( \varepsilon_i \mid \varepsilon_j \right)+\left( \varepsilon_i \mid {\rm e}_{k+1} \right)=0\\ &\Longleftrightarrow& \alpha_i \left\|\varepsilon_i\right\|^2+\left( \varepsilon_i \mid {\rm e}_{k+1} \right)=0\newline &\Longleftrightarrow& \alpha_i = -\left( \varepsilon_i \mid {\rm e}_{k+1} \right)\end{aligned}\] car \(\left\|\varepsilon_i\right\|=1\). On considère alors le vecteur \(\widetilde\varepsilon_{k+1}\) donné par \[\widetilde \varepsilon_{k+1} = e_{k+1}-\sum_{i=1}^n \left( \varepsilon_i \mid {\rm e}_{k+1} \right) \varepsilon_i.\] et soit \(\varepsilon_{k+1}=\dfrac{\widetilde\varepsilon_{k+1}}{\left\|\widetilde \varepsilon_{k+1}\right\|}\) Par construction, les vecteurs du système \(\left(\varepsilon_1,\dots, \varepsilon_{k+1}\right)\) sont deux à deux orthogonaux et unitaires. Cette famille est donc orthonormale. De plus, pour tout \(i\in\llbracket 1,k\rrbracket,\quad Vect\left(\varepsilon_1,\dots,\varepsilon_i\right)=Vect\left(e_1,\dots,e_i\right)\) et il est clair que \(Vect\left(\varepsilon_1,\dots,\varepsilon_{k+1}\right)=Vect\left(e_1,\dots,e_{k+1}\right)\). Enfin, quitte à considérer \(-\varepsilon_{k+1}\) plutôt que \(\varepsilon_{k+1}\), on peut supposer que \(\left( e_{k+1} \mid \varepsilon_{k+1} \right)>0\).
En appliquant cet algorithme jusqu’au rang \(n\), on construit la famille \(\varepsilon\) proposée.
L’algorithme de construction de la
base orthonormale est aussi important que l’énoncé du théorème.
La matrice de passage de \(e\) vers \(\varepsilon\) est triangulaire supérieure.
(Pour orthonormaliser une famille de
vecteurs ). On souhaite appliquer l’algorithme de Schmidt à la base
\(\left(e_1,\dots,e_n\right)\) de \(E\). Pour ce faire :
On pose \(\varepsilon_1=\dfrac{e_1}{\left\|e_1\right\|}\).
On suppose \(\varepsilon_1,\dots,\varepsilon_k\) construits. On calcule le vecteur : \(\boxed{\widetilde\varepsilon_{k+1} = e_{k+1}-\sum_{i=1}^n \left( \varepsilon_i \mid {\rm e}_{k+1} \right) \varepsilon_i}\) et on pose : \(\boxed{\varepsilon_{k+1}=\dfrac{\widetilde\varepsilon_{k+1}}{\left\|\widetilde \varepsilon_{k+1}\right\|}}\).
Si \(\left( e_{k+1} \mid \varepsilon_{k+1} \right)<0\) alors on remplace \(\varepsilon_{k+1}\) par \(-\varepsilon_{k+1}\).
La troisième étape du procédé d’orthonormalisation est facultative. Si on ne l’effectue pas, la base construite est encore orthonormale.
On peut aussi ne pas normaliser le vecteur \(\widetilde\varepsilon_i\) dans la deuxième étape de l’algorithme. Dans ce cas la base construire n’est pas orthonormale mais orthogonale et la formule donnant \(\varepsilon_{k+1}\) en fonction de \(e_{k+1}\), \(\varepsilon_1\),...,\(\varepsilon_k\) est légérement changée (exercice!).
La matrice de passage de \(e\) vers \(\varepsilon\) est triangulaire supérieure.
Soit l’espace \(E=\mathbb{R}^{3}\) muni du produit scalaire
usuel. Soient les vecteurs \(e_1=(2,0,0)\), \(e_2=(1,1,1)\) et \(e_3=(0,1,2)\). Construisons une base
orthonormale à partir de \(e=(e_1,e_2,e_3)\). D’après l’algorithme
d’orthonormalisation de Schmidt :
La famille \(\left(\varepsilon_1,\varepsilon_2,\varepsilon_3\right)\)
est une base orthonormale de \(E\).
On pose \(\boxed{\varepsilon_1=\left(1,0,0\right)}\).
On a \(\widetilde\varepsilon_2=e_2-\left( \varepsilon_1 \mid e_2 \right) \varepsilon_1=\left(0,1,1\right)\) donc \(\boxed{\varepsilon_2=\dfrac{\sqrt 2}{2}\left(1,0,0\right)}\).
De même \(\widetilde\varepsilon_3=e_3-\left( \varepsilon_1 \mid e_3 \right) \varepsilon_1 -\left( \varepsilon_2 \mid e_3 \right) \varepsilon_2 =\left(0,-\dfrac{1}{2},\dfrac{1}{2}\right)\) donc \(\boxed{\varepsilon_3=\dfrac{\sqrt 2}{2}\left(0,-1,1\right)}\).
> with(linalg):
Warning, the protected names norm and trace have been redefined and
unprotected
> e1 := vector([1,0,0]);
e1 := [1, 0, 0]
> e2 := vector([1,1,1]);
e2 := [1, 1, 1]
> e3 := vector([0,1,2]);
e3 := [0, 1, 2]
> GramSchmidt([e1,e2,e3],normalized);
[ [ 1 (1/2) 1 (1/2)] [ 1 (1/2) 1 (1/2)]]
[[1, 0, 0], [0, - 2 , - 2 ], [0, - - 2 , - 2 ]]
[ [ 2 2 ] [ 2 2 ]]
Conséquences
(Théorème de la base orthonormale
incomplète). Toute famille orthonormale \(\left(\varepsilon_1,\dots,\varepsilon_p\right)\)
d’un espace euclidien \(E \neq
\{0_E\}\) de dimension \(n\)
(\(p\leqslant n\)) peut être complétée
par des vecteurs \(\varepsilon_{p+1},\dots,\varepsilon_n\) de
\(E\) en sorte que la famille \(\left(\varepsilon_1,\dots,\varepsilon_n\right)\)
soit une base orthonormale de \(E\).
En appliquant le théorème de la base
incomplète, on peut compléter la famille orthonormale (et donc libre)
\(\left(\varepsilon_1,\dots,\varepsilon_p\right)\)
par des vecteurs \(e_{k+1},\dots,e_n\)
en une base \(e=\left(\varepsilon_1,\dots,\varepsilon_k,e_{k+1},\dots,e_n\right)\)
de \(E\). On applique le procédé
d’orthonormalisation de Schmidt à cette base , on peut construire des
vecteurs \(\varepsilon_{k+1},\dots,\varepsilon_n\) de
\(E\) tels que la famille \(\left(\varepsilon_1,\dots,\varepsilon_n\right)\)
soit orthonormale et tel que \(Vect\left(\varepsilon_1,\dots,\varepsilon_n\right)=Vect\left(\varepsilon_1,\dots,\varepsilon_k,e_{
k+1},\dots,e_n\right)=E\). Cette famille est donc libre et
génératrice et forme une base orthonormale de \(E\).
(Existence d’une base orthonormale).
Tout espace euclidien \(E \neq
\{0_E\}\) possède une base orthonormale.
Soit \(e\) une base de \(E\). En appliquant le procédé
d’orthonormalisation de Schmidt à cette famille, on construit une
famille orthonormale \(\varepsilon\)
telle que \(Vect\left(\varepsilon\right)=Vect\left(e\right)=E\).
Cette famille est donc libre et génératrice. Elle forme une base
orthonormale de \(E\).
( Propriétés de l’orthogonal en dimension
finie). Soit \(F\) un sous-espace
vectoriel de dimension \(p\) de \(E\). Alors
\(\boxed{E= F\oplus F^{\perp}}\);
\(\dim F^{\perp}= n-p\);
\({(F^{\perp})}^{\perp}=F\).
Montrons que \(F\) et \(F^\perp\) sont supplémentaires dans \(E\).
On a : \(F\cap F^{\perp}=\left\{0\right\}\). En effet, si un vecteur \(x\) est à la fois dans \(F\) et dans l’orthognal de \(F\), il vérifie \(\left( x \mid x \right)=0\) et donc \(x=0\).
Montrons maitenant que \(E=F+F^\perp\). Comme \(F\) est de dimension \(p\), par application du théorème précédent, on peut trouver une base orthonormale \(\left(e_1,\dots,e_p\right)\) de \(F\). Soit \(x\in E\) et soit \(x'=\sum_{k=1}^p \left( x \mid e_k \right)e_k\). On vérifie facilement que \(x'\in F\) et que \(x-x' \in F^\perp\). Donc \(x=x+\left(x-x'\right)\in F+F^\perp\) et on a bien \(E=F+F^\perp\).
Un sous-espace vectoriel \(F\) d’un espace \(E\) de dimension finie possède, en général,
une infinité de supplémentaires. Si \(E\) est un espace euclidien, \(F\) n’admet qu’un et un seul supplémentaire
orthogonal : \(F^\perp\). Pour cette
raison, on dira que \(F^\perp\) est
supplémentaire orthogonal de \(F\) dans
\(E\).
(Théorème de Riesz). Soit \(E\) un espace euclidien et soit \(f\in E^{\star}\) une forme linéaire. Alors
il existe un unique vecteur \(z_f\in
E\) tel que \[\forall x\in E, \quad
f(x)=\left( z_f \mid x \right)\]
Pour tout \(z\in E\), posons : \[\varphi_z: \left\{ \begin{array}{ccl} E
& \longrightarrow & \mathbb{R} \\ x & \longmapsto &
\left( z \mid x \right) \end{array} \right. .\] Pour tout
\(z\in E\), \(\varphi_z\) est une forme linéaire. En
effet, fixons \(z\in E\). Pour tout
\(\alpha,\beta\in\mathbb{R}\) et pour
tout \(x,y\in E\) : \(\varphi_z\left(\alpha x+\beta y\right)=
\left( z \mid \alpha x+\beta y \right)=\alpha\left( z \mid x
\right)+\beta\left( z \mid y \right)=\alpha
\varphi_z\left(x\right)+\beta\varphi_z\left(y\right).\)
L’application \(\Phi\) donnée par \[\Phi: \left\{ \begin{array}{ccl} E &
\longrightarrow & E^* \newline z & \longmapsto &
\varphi_z \end{array} \right.\] est alors bien définie.
Montrons que c’est un isomorphisme d’espaces vectoriels.
si \(\alpha,\beta\in\mathbb{R}\) et \(x,y\in E\) alors \(\Phi\left(\alpha x+\beta y\right)=\varphi_{\alpha x+\beta y}=\left( \alpha x+\beta y \mid \cdot \right)=\alpha \left( x \mid \cdot \right) + \beta \left( y \mid \cdot \right)=\alpha \varphi_x + \beta \varphi_y=\alpha\Phi\left(x\right)+\beta \Phi\left(y\right)\).
soit \(x\in E\) tel que \(\Phi\left(x\right)=0\). Alors : \(\forall y\in E,\quad \left( x \mid y \right)=0\), et en particulier \(\left( x \mid x \right)=0\) ce qui n’est possible, par définition du produit scalaire que si \(x=0\).
comme \(\dim E=\dim E^*\) (voir l’exercice [exo_dual_dun_kev] page [exo_dual_dun_kev]), d’après le théorème de caractérisation des isomorphismes [caracterisation_des_isomorphismes], sachant que \(\Phi\) est injective, il vient que \(\Phi\) est aussi surjective.
Dans \(\mathbb{R}^{n}\) muni du produit scalaire
usuel, si l’on considère un hyperplan \(H\) d’équation : \[\alpha_1 x_1 + \cdots + \alpha_n x_n = 0\]
Alors cet hyperplan est orthogonal au vecteur \(n = (\alpha_1,\dots,
\alpha_n)\) : \(H =
\{n\}^{\perp}\).
Projecteurs et symétries orthogonaux
Projecteurs orthogonaux
(Projecteur orthogonal). Soit \(p\in L(E)\) un projecteur (c’est-à-dire une
endomorphisme \(p\) de \(E\) vérifiant \(p\circ p= p\)). On dit que \(p\) est un projecteur orthogonal
si et seulement si \(\operatorname{Ker}p\) et \(\mathop{\mathrm{Im}}p\) sont deux
sous-espaces orthogonaux de \(E\) :
\[\forall x\in \operatorname{Ker}p,~\forall
y\in \mathop{\mathrm{Im}}p, \quad\left( x \mid y \right)=0\]
Soit \(p\) un projecteur orthogonal et soit \(x\in E\). Alors \(\left( p\left(x\right) \mid x-p\left(x\right)
\right)=0\). En effet \(x-p\left(x\right) \in {\rm Ker}\,p = \mathop{\rm
Im}f^\perp\)
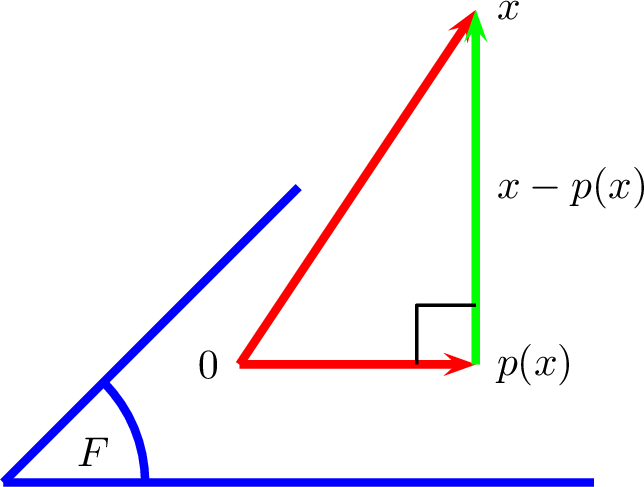
(Calcul du projeté orthogonal). Soit
\(F\) un sous-espace vectoriel de \(E\) et soit \(x
\in E\). On suppose que
alors le projeté orthogonal \(p(x)\)
du vecteur \(x\) sur le sous-espace
\(F\) vaut : \[\boxed{p(x) = \sum_{i=1}^p \left( x \mid
\varepsilon_i \right).\varepsilon_i}.\]
\((\varepsilon_1,\dots, \varepsilon_p)\) est une base orthonormale de \(F\)
D’après le théorème
[Calculs_dans_base_orthonormale] appliqué à \(p\left(x\right)\in
F\) et à la base orthonormale \(\varepsilon\) de \(F\) donnée : \[\begin{aligned}
p\left(x\right)&=& \sum_{i=1}^p \left( p\left(x\right) \mid
\varepsilon_i \right) \varepsilon_i \\
&=& \sum_{i=1}^p \left( x \mid \varepsilon_i \right)
\varepsilon_i -\sum_{i=1}^p
\left( x-p\left(x\right) \mid \varepsilon_i \right)
\varepsilon_i \newline
&=& \sum_{i=1}^p \left( x \mid \varepsilon_i \right)
\varepsilon_i\end{aligned}\] car \(x-p\left(x\right)\in {\rm Ker}\,p =
F^\perp\) et donc : \[\forall i
\in\llbracket 1,p\rrbracket,\quad \left( x-p\left(x\right) \mid
\varepsilon_i \right)=0.\]
(Le projeté \(p(x)\) réalise la meilleure approximation
de \(x\) par des vecteurs de \(F\)). Soit \(F\) un sous-espace vectoriel
de \(E\). Pour tout \(x\in E\), on pose : \[d(x,F)= \inf_{f\in F} \lVert x-f \rVert_{ }
.\] Alors :
\(d(x,F)\) est bien défini ;
\(d(x,F)=\lVert x-p(x) \rVert_{ }\) où \(p(x)\) est la projection orthogonale de \(x\) sur \(F\) ;
Si \(f\in F\), \(\lVert x-f \rVert_{ } \geqslant\lVert x-p(x) \rVert_{ }\) avec égalité si et seulement si \(f=p(x)\).
Soit \(x\in F\). Notons \(\mathscr F=\left\{\left\|x-f\right\|~|~ f \in F\right\}\). \(\mathscr F\) est une partie non vide de \(\mathbb{R}\) minorée par \(0\). Elle possède donc une borne inférieure et \(d(x,F)\) est bien défini.
D’après le théorème de Pythagore [theoreme_de_Pythagore], pour tout \(f\in F\) : \[\lVert x - f \rVert_{ }^2 = \lVert x - p(x) \rVert_{ }^2 + \lVert p(x) - f \rVert_{ }^2 \geqslant\lVert x - p(x) \rVert_{ }^2.\] Donc \(\left\|x-p\left(x\right)\right\|\) est un minorant de \(\mathscr F\). Mais comme \(p\left(x\right)\in F\), \(\left\|x-p\left(x\right)\right\|\in \mathscr F\) et est donc la borne inférieure de \(\mathscr F\). Il vient alors : \(d(x,F)=\lVert x-p(x) \rVert_{ }\).
On a de plus montré que si \(f\in F\), alors \(\lVert x-f \rVert_{ } \geqslant \lVert x-p(x) \rVert_{ }\) et on a égalité si et seulement si \(f=p(x)\).
Symétries orthogonales, réflexions
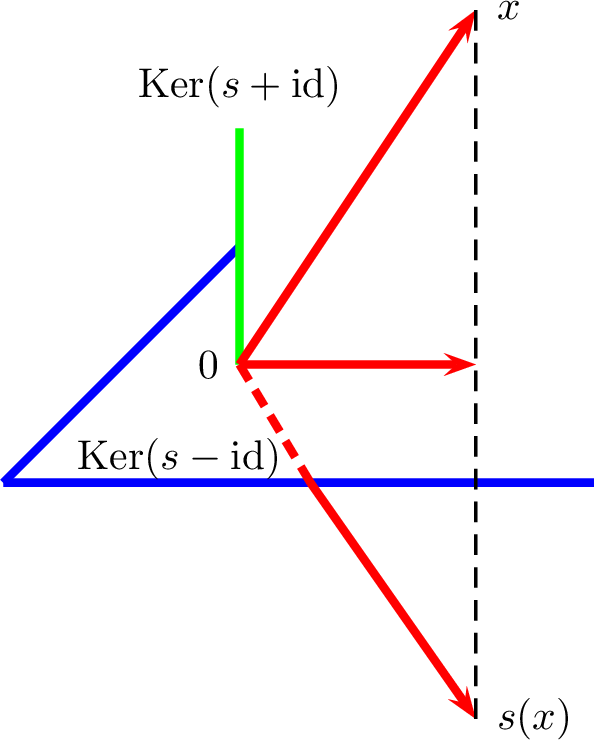
(Symétrie orthogonale, réflexion).
Soit \(s\in L(E)\) une symétrie
vectorielle (c’est-à-dire un endomorphisme de \(E\) tel que \(s\circ s =
\mathop{\mathrm{id}}\nolimits\)).
On dit que \(s\) est une symétrie orthogonale si et seulement si les deux sous-espaces vectoriels \(\operatorname{Ker}(s-\mathop{\mathrm{id}}\nolimits)\) et \(\operatorname{Ker}(s+\mathop{\mathrm{id}}\nolimits)\) sont orthogonaux.
On dit de plus que \(s\) est une réflexion si l’ensemble des vecteurs invariants de \(s\), \(\operatorname{Ker}(s-\mathop{\mathrm{id}}\nolimits)\) est un hyperplan de \(E\).
Endomorphismes orthogonaux, matrices orthogonales
Endomorphismes orthogonaux
On considère dans toute la suite un espace euclidien \(E\) muni d’un produit scalaire noté \(\left( . \mid . \right)\) et \(\lVert . \rVert_{ }\) la norme euclidienne associée. On note \(n\) la dimension de \(E\).
(Endomorphismes orthogonaux). Soit
\(u\in L(E)\). On dit que \(u\) est un endomorphisme
orthogonal (ou une isométrie) si \[\forall x\in E, \quad\lVert u(x) \rVert_{ } =
\lVert x \rVert_{ }.\] On note \(\mathrm{O}_{ }(E)\) l’ensemble des
endomorphismes orthogonaux de \(E\).
( Un endomorphisme orthogonal conserve le
produit scalaire). On
a l’équivalence : \[u \in \mathrm{O}_{ }(E)
\Longleftrightarrow
\forall (x,y)\in E^2, \quad\left( u(x) \mid u(y) \right) = \left( x
\mid y \right) .\]
Supposons que \(u\) est un endomorphisme orthogonal de \(E\). D’après l’identité de polarisation [regles_calcul_prod_scalaire], pour tout \(\left(x,y\right)\in E^2\) : \[\begin{aligned} \left( u\left(x\right) \mid u\left(y\right) \right) &=& \dfrac{1}{4}\left(\lVert u\left(x+y\right) \rVert_{ }^2 - \lVert u\left(x-y\right) \rVert_{ }^2\right)\\ &=& \dfrac{1}{4}\left(\lVert x+y \rVert_{ }^2 - \lVert x-y \rVert_{ }^2\right)\newline &=& \left( x \mid y \right).\end{aligned}\]
Supposons que \(u\) préserve le produit scalaire alors pour tout \(x\in E\) : \[\begin{aligned} \lVert u(x) \rVert_{ } =\sqrt{\left( u\left(x\right) \mid u\left(x\right) \right)}=\sqrt{\left( x \mid x \right)}=\left\|x\right\|\end{aligned}\] et donc \(u\in \mathrm{O}_{ }(E)\).
(Les endomorphismes orthogonaux sont des
automorphismes). Soit \(u\in \mathrm{O}_{
}(E)\) un endomorphisme orthogonal de \(E\) alors \(u\) est un automorphisme de \(E\) et \(u^{-1}\in \mathrm{O}_{ }(E)\) .
Soit \(x\in
{\rm Ker}\,u\) alors \[\left\|x\right\|=\left\|u\left(x\right)\right\|=0\]
et d’après les propriétés de la norme [axiomes_norme], on peut
affirmer que \(x=0\). Donc \({\rm Ker}\,u=\left\{0\right\}\) et \(u\) est injectif. D’après la
caractérisation des automorphismes d’un \(\mathbb{K}\)-espace vectoriel de dimension
finie (corollaire [carac_autom15:26:38] page
[carac_autom15:26:38]), \(u\)
est un automorphisme de \(E\). Enfin,
considérons \(x\in E\) et notons \(y=u\left(x\right)\). \(u\) étant un endomorphisme orthogonal de
\(E\), on a \(\left\|x\right\|=\left\|y\right\|\). Donc,
comme \(u^{-1}\left(y\right)=x\), il
vient que \(\left\|u^{-1}\left(y\right)\right\|=\left\|x\right\|=\left\|y\right\|\)
et \(u^{-1}\) est bien lui aussi un
endomorphisme orthonal de \(E\).
(Groupe orthogonal). \((\mathrm{O}_{ }(E), \circ)\) est un
sous-groupe du groupe linéaire \((GL_{
}\left(E\right),\circ)\). On l’appelle le groupe
orthogonal de \(E\).
\(\mathrm{O}_{ }(E)\) est un sous-ensemble
non vide de \({\rm GL}(E)\) car il
contient \(\mathop{\mathrm{id}}\nolimits_E\). D’après
le théorème [Caracterisation_des_sous_groupes], il suffit de
prouver que pour tout \(u,v\in \mathrm{O}_{
}(E)\), \(u\circ v^{-1}\in
\mathrm{O}_{ }(E)\). Mais d’après la proposition précédente,
\(v^{-1}\) est aussi une isométrie de
\(E\) et pour tout \(x\in E\), on a : \[\left\|u\circ
v^{-1}\left(x\right)\right\|=\left\|u\left(v^{-1}\left(x\right)\right)\right\|=\left\|v^{-1}\left(x\right)\right\|=\left\|x\right\|\]
ce qui prouve que \(u\circ v^{-1}\in
\mathrm{O}_{ }(E)\). Le couple \((\mathrm{O}_{ }(E), \circ)\) est donc un
sous-groupe de \((GL_{
}\left(E\right),\circ)\).
(Une caractérisation pratique des
automorphismes
orthogonaux).
Soit \(u\in\mathfrak{L}\left(E\right)\)
et soit \(e=\left(e_1,\dots,e_n\right)\) une base
orthonormale de \(E\). On a équivalence
entre :
\(u\in\mathrm{O}_{ }(E)\),
\(\left(u\left(e_1\right),\dots,u\left(e_n\right)\right)\) est encore une base orthonormale de \(E\).
Si \(u\in \mathrm{O}_{ }(E)\), d’après la proposition [endo_ortho_conservent_prod_scal], pour tout \(i,j\in\llbracket 1,n\rrbracket\) : \[\left( u\left(e_i\right) \mid u\left(e_j\right) \right) =\left( e_i \mid e_j \right)=\begin{cases} 0 \textrm{ si } i\neq j \\ 1 \textrm{ si } i=j\end{cases}\] ce qui prouve que la famille \(\left(u\left(e_1\right),\dots,u\left(e_n\right)\right)\) est une base orthonormale de \(E\).
Si l’image par \(u\) de la base orthonormale \(e=\left(e_1,\dots,e_n\right)\) est encore orthonomale alors pour \(x=\sum_{i=1}^n x_i e_i\in E\) et par bilinéarité du produit scalaire : \[\begin{aligned} \left\|u\left(x\right)\right\|^2&=&\left( u\left(x\right) \mid u\left(x\right) \right)\\ &=&\sum_{i,j\in\llbracket 1,n\rrbracket}{ x_i x_j \left( u\left(e_i\right) \mid u\left(e_j\right) \right)}\\ &=& \sum_{i\in\llbracket 1,n\rrbracket}{ x_i^2 \left( u\left(e_i\right) \mid u\left(e_i\right) \right)}\\ &=& \sum_{i\in\llbracket 1,n\rrbracket}{ x_i^2}\newline &=&{\left\|x\right\|}^2.\end{aligned}\] Donc \(u\in\mathrm{O}_{ }(E)\).
Matrices orthogonales
(Matrices orthogonales). On dit qu’une
matrice \(A\in
\mathfrak{M}_{n}(\mathbb{\mathbb{R} })\) est orthogonale
si et seulement si : \[{A}^{\mathrm{T}}A=I_n
.\] On note \(\mathrm{O}_{n}(\mathbb{R}
)\) l’ensemble des matrices orthogonales.
Une matrice orthogonale est
inversible et \[A^{-1}={A}^{\mathrm{T}}.\] Ce qui montre
qu’elle vérifie également \[A{A}^{\mathrm{T}}=I_n.\]
( Caractérisation pratique des matrices
orthogonales).
Soit \(A=(a_{ij}) \in
\mathfrak{M}_{n}(\mathbb{\mathbb{R} })\). Alors \(A\) est une matrice orthogonale si et
seulement si ses vecteurs colonnes \((C_1,\dots,C_n)\) forment une base
orthonormale pour le produit scalaire usuel de \(\mathbb{R}^{n}\), c’est-à-dire : \[\forall (p,q)\in [\kern-0.127em[ 1, n
]\kern-0.127em]^2, \quad p\neq q \Rightarrow \sum_{i=1}^n
a_{ip}a_{iq}=0 \quad \textrm{ et} \quad
\forall j \in [\kern-0.127em[ 1, n ]\kern-0.127em], \quad\sum_{i=1}^n
a_{ij}^2=1.\]
Ces formules sont une conséquence
directe de la définition du produit matriciel et de l’égalité : \(A{A}^{\mathrm{T}}=I_n\)
(La matrice d’une isométrie dans une base
orthonormale est
orthogonale). On
considère une base orthonormale \(e=\left(e_1,\dots,e_n\right)\) d’un espace
euclidien \(E\), et un endomorphisme
\(u \in L(E)\). Notons \(A = \mathop{\mathrm{Mat}}_{e}(u)\). On a
équivalence entre :
\(u\) est un automorphisme orthogonal.
\(A\) est une matrice orthogonale.
Notons \(A=\left(a_{ij}\right)_{\left(i,j\right)\in\llbracket
1,n\rrbracket^2}\). Par bilinéarité du produit scalaire, il
vient, pour tout \(i,j\in\llbracket
1,n\rrbracket\) : \[\begin{aligned}
\left( u\left(e_i\right) \mid u\left(e_j\right)
\right)&=&\sum_{k=1}^n\sum_{k'=1}^n a_{ki}a_{k'j}
\left( e_k \mid e_k' \right)\end{aligned}\] et donc, comme
\(e\) est orthonormale : \[\begin{aligned}
\left( u\left(e_i\right) \mid u\left(e_j\right)
\right)&=&\sum_{k=1}^n a_{ki}a_{kj}
\quad \left(\star\right).\end{aligned}\]
Supposons que \(u\in L(E)\) est une isométrie de \(E\). Alors, comme les isométries conservent le produit scalaire, l’égalité \(\left(\star\right)\) devient, pour tout \(i,j\in\llbracket 1,n\rrbracket\) : \[\begin{aligned} \delta_{i,j}=\left( {e_i} \mid {e_j} \right)=\sum_{k=1}^n a_{ki}a_{kj} \end{aligned}\] et donc, d’après [caracterisation_pratique_matrice_orthogonale], \(A\) est orthogonale.
Réciproquement, si \(A\) est orthogonale alors en utilisant à nouveau \(\left(\star\right)\) et la proposition [caracterisation_pratique_matrice_orthogonale], on trouve, pour tout \(i,j\in\llbracket 1,n\rrbracket\) : \[\begin{aligned} \left( u\left(e_i\right) \mid u\left(e_j\right) \right)&=& \left( e_i \mid e_j \right) \end{aligned}\] et donc la famille \(\left(u\left(e_1\right),\dots,u\left(e_n\right)\right)\) est une base orthonormale de \(E\). On applique alors la proposition [Caracterisation_pratique_autom_ortho] et \(u\) est un automorphisme orthogonal.
Le résultat précédent est faux si
la base \(\varepsilon\) n’est pas
orthonormale.
(Caractérisation des matrices de passage
entre bases orthonormales).
Soit \(e\) une base orthonormale de \(E\) et \(f\) une base de \(E\). Soit \(P=P_{e\rightarrow f}\) la matrice de
passage entre ces deux bases. On a équivalence entre :
\(f\) est une base orthonormale.
P est une matrice orthogonale.
Supposons que \(f\) est orthonormale. Soit \(u\) l’endomorphisme de \(E\) donné par : \[\forall i\in\llbracket 1,n\rrbracket,\quad u\left(e_i\right)=f_i .\] D’après la proposition [Caracterisation_pratique_autom_ortho], \(u\) est un automorphisme orthogonal de \(E\). Mais \(P_{e\rightarrow f}=\textrm{ Mat}_{e}\left(f\right)=\textrm{ Mat}_{e}\left(u\right)\) et donc, d’après la dernière proposition, \(P=P_{e\rightarrow f}\) est orthogonale.
De la même façon, si \(P\) est orthogonale, alors il en est de même de \(u\) et comme l’image d’une base orthonormale par un élément de \(\mathrm{O}_{ }(E)\) est orthonormale, \(f\) est orthonormale.
Etude du groupe orthogonal
Soit \(A\in\mathop{\mathrm{Mat}}_n\left(\mathbb{R}\right)\)
une matrice orthogonale. Comme \(A.{A}^{\mathrm{T}}=I_n\) et que \(\mathop{\rm det}\left(A\right)=\mathop{\rm
det}\left({A}^{\mathrm{T}}\right)\), il vient que : \(\mathop{\rm det}\left(A\right)=\pm 1\).
(Groupe spécial orthogonal \({O}_{n}^{+}(\mathbb{R} )\)). Soit une
matrice orthogonale \(A \in
\mathrm{O}_{n}(\mathbb{R} )\). Alors \(\mathop{\rm det}(A) = \pm 1\). On définit
les sous-ensembles de \(\mathrm{O}_{n}(\mathbb{R} )\) suivants :
\[{O}_{n}^{+}(\mathbb{R} )= \{A \in
\mathrm{O}_{n}(\mathbb{R} ) \mid \mathop{\rm det}A = +1 \} \quad
\mathrm{O}_{n}^{-}(\mathbb{R} ) = \{A \in \mathrm{O}_{n}(\mathbb{R} )
\mid \mathop{\rm det}A = -1 \}\] Les matrices de \({O}_{n}^{+}(\mathbb{R} )\) sont appelées
spéciales orthogonales. L’ensemble \({O}_{n}^{+}(\mathbb{R} )\) est un
sous-groupe du groupe orthogonal \((\mathrm{O}_{n}(\mathbb{R} ), \times)\).
On a déjà que \(I_n\in {O}_{n}^{+}(\mathbb{R} )\). Soient
\(A,B\in {O}_{n}^{+}(\mathbb{R} )\)
alors \(A.B^{-1}\) est encore élement
de \(\mathrm{O}_{n}(\mathbb{R} )\) car
ce dernier est un groupe. De plus, avec les propriétés du déterminant
\(\mathop{\rm
det}\left(A.B^{-1}\right)=1\) donc \(A.B^{-1}\in
{O}_{n}^{+}(\mathbb{R} )\) et \({O}_{n}^{+}(\mathbb{R} )\) est bien un
sous-groupe de \(\mathrm{O}_{n}(\mathbb{R}
)\).
(Critère pour reconnaître les matrices de
\({O}_{n}^{+}(\mathbb{R} )\)).
Soit une matrice orthogonale \(A \in
\mathrm{O}_{n}(\mathbb{R} )\). Soit un coefficient \(a_{ij} \neq 0\) de la matrice \(A\) et \(A_{ij}\) le cofacteur associé.
Si \(A \in {O}_{n}^{+}(\mathbb{R} )\), alors \(a_{ij} = A_{ij}\) ;
si \(A \in \mathrm{O}_{n}^{-}(\mathbb{R} )\), alors \(a_{ij} = - A_{ij}\).
Soit \(A=\left(a_{ij}\right)\in\mathrm{O}_{n}(\mathbb{R}
)\). L’inverse de la matrice \(A\) est \({A}^{\mathrm{T}}\). Cet inverse est aussi
donné par \({\left(\mathop{\rm
Com}{A}\right)}^{\mathrm{T}}/\mathop{\rm det}{A}\) où \(\mathop{\rm Com}{A}\) est la comatrice de
\(A\) (voir section
[Inversion_de_matrice_comatrice] page
[Inversion_de_matrice_comatrice]). Alors par identification des
coefficients dans ces deux matrices, pour tout \(\left(i,j\right)\in\llbracket
1,n\rrbracket^2\), on a : \(a_{ij}=A_{ij}/\mathop{\rm det}A\). Si \(A \in
{O}_{n}^{+}(\mathbb{R} )\), alors \(\mathop{\rm det}A=1\) et \(a_{ij} = A_{ij}\). Si \(A \in
\mathrm{O}_{n}^{-}(\mathbb{R} )\), alors \(\mathop{\rm det}A=-1\) et \(a_{ij} = - A_{ij}\).
En pratique, pour vérifier qu’une
matrice \(A \in \mathrm{O}_{n}(\mathbb{R}
)\) est spéciale orthogonale, on calcule le déterminant \(\Delta_{11}=m_{11}\) et on compare son
signe avec celui du coefficient \(a_{11}\).
(Isométries directes et indirectes).
Soit une isométrie \(u \in \mathrm{O}_{
}(E)\) d’un espace euclidien orienté \(E\). Alors \(\mathop{\rm det}(u) = \pm 1\). On dit que
\(u\) est une isométrie
directe de \(E\) lorsque \(\mathop{\rm det}(u) =
+1\), et une isométrie indirecte lorsque \(\mathop{\rm det}(u) = -1\). On note \(\mathrm{O}_{ }^{+}(E)\) l’ensemble des
isométries directes, et \(\mathrm{O}_{
}^{-}(E)\) l’ensemble des isométries indirectes de \(E\). L’ensemble \(\mathrm{O}_{ }^{+}(E)\) est un sous-groupe
du groupe orthogonal \((\mathrm{O}_{ }(E),
\circ)\).
Si \(\varepsilon\) est une base orthonormale de
\(E\), et si \(U\) est la matrice de l’isométrie \(u\) dans la base \(\varepsilon\), alors \[\underset{(i)}{\bigl( u \textrm{ isométrie
directe } \bigr)} \Longleftrightarrow \underset{(ii)}{\bigl( U \in
{O}_{n}^{+}(\mathbb{R} ) \bigr)}.\]
Dans un espace vectoriel euclidien
orienté, une isométrie directe transforme une base orthonormée directe
en une base orthonormée directe. (et une isométrie directe transforme
une base orthonormée directe en une base orthonormée indirecte.)
Dans un espace vectoriel euclidien
orienté, tout endomorphisme qui transforme une base orthonormée directe
en une base orthonormée directe est une isométrie directe.
Etude du groupe orthogonal en dimension \(2\).
On considère dans tout ce paragraphe un espace euclidien orienté \(E\) de dimension \(2\).
(Etude de \({O}_{2}^{+}(\mathbb{R} )\)).
Les matrices de \({O}_{2}^{+}(\mathbb{R} )\) sont de la forme \[R_{\theta}=\boxed{\begin{pmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix}}\] où \(\theta\in\mathbb{R}\).
\[\boxed{R_{\theta}\times R_{\theta'}=R_{\theta + \theta'}} .\]
\[\boxed{R_{\theta}^{-1}=R_{-\theta}} .\]
L’application \[\varphi: \left\{ \begin{array}{ccl} (\mathbb{R} ,+) & \longrightarrow & ({O}_{2}^{+}(\mathbb{R} ),\times) \newline \theta & \longmapsto & R_{\theta} \end{array} \right.\] est un morphisme de groupes de noyau \(2\pi\mathbb{Z}\).
Soit \(A=\begin{pmatrix} a&b\\c&d \end{pmatrix} \in\mathfrak{M}_{2}\left(\mathbb{R}\right)\). On a les équivalences : \[\begin{aligned} & &A\in{O}_{2}^{+}(\mathbb{R} ) \\ &\Longleftrightarrow& A{A}^{\mathrm{T}}=1 \quad \textrm{ et} \quad\mathop{\rm det}A=1 \\ &\Longleftrightarrow& \begin{cases}a^2+b^2&=1\\c^2+d^2&=1\\ac+bd&=0\\ad-bc&=1\end{cases} \end{aligned}\] Des deux premières équations, on tire l’existence de \(\theta\) et \(\theta'\in\mathbb{R}\) tels que : \(a=\cos \theta\), \(b=\sin \theta\), \(c=\cos \theta'\) et \(d=\sin \theta'\). La quatrième équation devient alors \(\cos \theta \sin \theta'- \sin\theta \cos \theta'=1\) c’est-à-dire \(\sin \left(\theta'-\theta\right)=1\) et la troisième devient \(\cos \theta\cos \theta'+\sin\theta \sin\theta'=0\) c’est-à-dire \(\cos\left(\theta'-\theta\right)=0\). Il vient alors \(\theta'=\theta+\dfrac{\pi}{2} ~\left[2\pi\right]\) et on obtient : \[A\in{O}_{2}^{+}(\mathbb{R} ) \Longleftrightarrow A= \begin{pmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{pmatrix} \textrm{ où } \theta\in\mathbb{R}\]
Cette formule est une conséquence directe du premier point et des formules d’addition pour le cosinus et le sinus.
D’après la formule précédente, on a : \(R_{\theta}R_{-\theta}=R_{\theta-\theta}=R_0=I_2\) donc \(R_{\theta}^{-1}=R_{-\theta}\).
Soient \(\theta,\theta'\in\mathbb{R}\). On a : \[\varphi\left(\theta+\theta'\right)=R_{\theta+\theta'}=R_{\theta}\times R_{\theta'}=\varphi\left(\theta\right)\varphi\left(\theta'\right)\] donc \(\varphi\) est bien un morphisme de groupe. On a par ailleurs les équivalences : \[\begin{aligned} \varphi\left(R_\theta\right)=I_2 \Longleftrightarrow\begin{cases}\cos \theta&=1\newline \sin\theta&=0 \end{cases} \Longleftrightarrow\theta=0~\left[2\pi\right]\end{aligned}\] donc \(\operatorname{Ker}\varphi=2\pi\mathbb{Z}\).
(Rotations vectorielles). Soit \(E\) un espace euclidien de dimension \(2\) orienté et \(u\in \mathrm{O}_{ }^{+}(E)\) une isométrie
directe. Alors il existe un unique \(\theta\in[0,2\pi[\) tel que pour toute
base orthonormale directe \(\varepsilon\) de \(E\), \[Mat_{\varepsilon}(u)=\begin{pmatrix} \cos\theta
& -\sin\theta \newline
\sin\theta & \cos\theta \end{pmatrix} .\] On dit que
\(u\) est la rotation vectorielle
d’angle \(\theta\) et on note \(u = r_{\theta}\).
C’est une conséquence directe du
théorème précédent et du théorème
[la_matrice_dune_isom_est_orthogonale].
(Angle de deux vecteurs). Soit \(E\) un espace euclidien orienté de
dimension \(2\) et \((U,V)\in
E^2\) deux vecteurs non-nuls. On définit \[u=\dfrac{U}{\lVert U \rVert_{ }}, \quad
v=\dfrac{V}{\lVert V \rVert_{ }}.\] Alors il existe une unique
rotation \(r\in {O}_{2}^{+}(\mathbb{R}
)\) telle que \(v=r(u)\). Si
\(\theta\) est l’angle de la rotation
\(\theta \in [0,2\pi[\), on note \[\widehat{(U,V)}=\theta\] l’angle orienté
des vecteurs \((U,V)\). On a alors :
\[\boxed{\mathop{\mathrm{Det}}(U,V)=\lVert U
\rVert_{ }\lVert V \rVert_{ }\sin\theta } \quad \textrm{ et} \quad
\boxed{\left( U \mid V \right)=\lVert U \rVert_{ }\lVert V \rVert_{
}\cos\theta}.\]
On applique le procédé d’ortonormalisation de Schmidt [Procede_orthonomalisation_Schmidt] et on complète les vecteurs \(u\) et \(v\) en deux bases \(e=\left(u,u'\right)\) et \(e'=\left(v,v'\right)\) orthonormales directes du plan. D’après la proposition [matrice_de_passage_entre_bases_orthonormales], la matrice de passage \(A\) de \(e\) à \(e'\) est orthogonale. Comme les bases sont directes, on a de plus \(\mathop{\rm det}A=1\). En résumé : \(A\in {O}_{2}^{+}(\mathbb{R} )\). Considérons alors l’endomorphisme \(\varphi\) de \(E\) tel que \(\mathop{\mathrm{Mat}}_{e' \leftarrow e}\left(u\right)=A\). D’après la propriété précédente, \(\varphi\) est une rotation du plan. On a de plus \(\varphi\left(u\right)=v\).
Si \(\varphi\) et \(\varphi'\) sont deux rotations du plan envoyant \(u\) sur \(v\), alors, avec les notations précédentes, \(\varphi\left(u\right)=\varphi'\left(u\right)\) et comme les rotations conservent le produit scalaire et l’orientation, \(\varphi\left(u'\right)=\varphi'\left(u'\right)\). Comme les endomorphismes \(\varphi\) et \(\varphi'\) sont égaux sur les vecteurs d’une base de \(E\), ils sont égaux sur \(E\) : \(\varphi=\varphi'\).
On utilise ces formules pour
déterminer l’angle entre deux vecteurs. Par exemple dans \(\mathbb{R}^{2}\) euclidien orienté usuel,
quel est l’angle entre les vecteurs \(U=(1,1)\) et \(V=(0,1)\) ?
(Etude de \(O_2^{-}(\mathbb{R} )\) ). Considérons
la matrice \(P=\begin{pmatrix}
1&0\\0&-1\end{pmatrix} \in \mathrm{O}_{2}^{-}(\mathbb{R}
)\). L’application \[\Delta :
\left\{ \begin{array}{ccl} {O}_{2}^{+}(\mathbb{R} ) &
\longrightarrow & \mathrm{O}_{2}^{-}(\mathbb{R} ) \\ A &
\longmapsto & AP \end{array} \right.\] est une bijection.
Toute matrice de \(\mathrm{O}_{2}^{-}(\mathbb{R} )\) est de la
forme \[B=\begin{pmatrix} \cos\theta &
\sin\theta \newline \sin\theta &
-\cos\theta \end{pmatrix} .\]
Laissée en exercice au lecteur.
(Isométries indirectes et réflexion).
Une isométrie
indirecte d’un espace euclidien orienté de dimension \(2\) est une symétrie orthogonale par
rapport à une droite, c’est-à-dire une réflexion.
La matrice d’une isométrie indirecte
\(u\) dans une base orthonormale \(e=\left(e_1,e_2\right)\) étant de la forme
\(A=\begin{pmatrix} \cos\alpha &
\sin\alpha \\
\sin\alpha &
-\cos\alpha \end{pmatrix}\) et cette matrice vérifiant \(A^2=A\), on en déduit que \(u\) est une symétrie par rapport à \({\rm
Ker}\,\left(u-\mathop{\mathrm{id}}\nolimits\right)\)
parallèlement à \({\rm Ker}\,
\left(u+\mathop{\mathrm{id}}\nolimits\right)\). Déterminons \({\rm
Ker}\,\left(u-\mathop{\mathrm{id}}\nolimits\right)\). On a, dans
la base \(e\) : \[\begin{aligned}
& &U=xe_1+ye_2\in {\rm
Ker}\,\left(u-\mathop{\mathrm{id}}\nolimits\right)\\
&\Longleftrightarrow& \begin{cases} \left(\cos \alpha -1
\right)x+\sin\alpha ~y =0 \\ \sin \alpha ~x
-\left(\cos \alpha +1\right)y=0 \end{cases}\\
&\Longleftrightarrow& \begin{cases} \sin\dfrac{\alpha}{2}\left(
\sin\dfrac{\alpha }{2} ~x-\cos
\dfrac{\alpha}{2} ~y \right) =0\\ \cos\dfrac{\alpha}{2}\left(
\sin\dfrac{\alpha }{2}
~x-\cos \dfrac{\alpha}{2} ~y \right) =0 \end{cases} \\
&\Longleftrightarrow& \sin\dfrac{\alpha }{2} ~x-\cos
\dfrac{\alpha}{2} ~y =0
\end{aligned}\] car on ne peut avoir en même temps \(\sin\dfrac{\alpha }{2}=0\) et \(\cos\dfrac{\alpha }{2}=0\). On en déduit
que \({\rm
Ker}\,\left(u-\mathop{\mathrm{id}}\nolimits\right)\) est la
droite vectorielle d’équation polaire \(\theta=\dfrac{\alpha}{2}\). On montrerait
de même que \(U=xe_1+ye_2\in {\rm
Ker}\,\left(u-\mathop{\mathrm{id}}\nolimits\right)\) si et
seulement si \(\sin\dfrac{\alpha }{2} ~x+\cos
\dfrac{\alpha}{2} ~y =0\). Les deux droites vectorielles \({\rm
Ker}\,\left(u-\mathop{\mathrm{id}}\nolimits\right)\) et \({\rm
Ker}\,\left(u-\mathop{\mathrm{id}}\nolimits\right)\) sont bien
orthogonales et \(u\) est une réflexion
du plan.
(Décomposition des rotations). Soit
\(E\) un espace euclidien orienté de
dimension \(2\).
Toute rotation de \(E\) s’écrit comme composée de deux réflexions.
Réciproquement, tout produit de réflexion est une rotation.
Soit \(r\) une rotation et \(s\) une réflexion de \(E\). Posons \(t=s^{-1}\circ r\). \(t\) est une isométrie de \(E\) et \(\mathop{\rm det}t = \mathop{\rm det}\left(s^{-1}\right)\mathop{\rm det}u=-1\), donc \(t\) est indirecte. En vertu de la proposition [isometrie_indirecte_egale_reflexion], \(t\) est une réflexion et \(r=s\circ t\) est bien la composée de deux réflexions.
Réciproquement, si \(s\) et \(t\) sont deux réflexions de \(E\) alors \(s \circ t\) est une isométrie directe de \(E\), c’est-à-dire une rotation.
Les réflexions engendrent le groupe
orthogonal \(O(E_2)\). Toute isométrie
de \(E_2\) s’écrit comme un produit de
\(1\) ou \(2\) réflexions.
Etude du groupe orthogonal en dimension 3
On considère dans tout ce paragraphe un espace euclidien orienté \(E\) de dimension \(3\).
Produit mixte, produit vectoriel
(Déterminant dans une base orthonormale
directe). Soit \(u,v,w\) trois
vecteurs. Le déterminant de ces trois vecteurs exprimé dans une base
orthonormale directe ne dépend pas de la base orthonormale directe
choisie.
On utilise la formule de changement
de base : \[\mathop{\rm
det}_{e'}\left(x_1,\dots,x_n\right)=\mathop{\rm
det}_{e'}\left(e_1,\dots,e_n\right)\times
\mathop{\rm det}_e\left(x_1,\dots,x_n\right).\] La matrice de
passage \(P_{e' \gets e}\) de \(e\) vers \(e'\) est donc aussi la matrice dans la
base \(e\) de l’endomorphisme qui
transforme \(e\) en \(e'\), donc qui transforme une base
orthonormée directe en une base orthonormée directe. C’est donc une
matrice de \(O^+(E)\). Elle a donc un
déterminant égal à \(1\). Donc \(\mathop{\rm
det}_{e'}\left(x_1,\dots,x_n\right)= \mathop{\rm
det}_e\left(x_1,\dots,x_n\right)\). Ce qu’il fallait vérifier.
La propriété précédente permet d’énoncer la
(Produit mixte). Soient \(u,v,w\) trois vecteurs. On appelle produit
mixte de \((u,v,w)\) le déterminant de
\((u,v,w)\) exprimé dans une base
orthonormée directe. On le note \([u,v,w]\).
Les propriétés du determinant permettent d’énoncer :
(Propriétés du produit mixte). Soit
\((u,v,w)\in E^3\).
\([u,v,w]\neq0\) si et seulement si \((u,v,w)\) est une base de \(E\).
\([u,v,w] = -[v,u,w]\).
\(w \mapsto [u,v,w]\) est une forme linéaire.
D’après le théorème de Riesz, il existe un unique vecteur \(x\in E\) tel que \(\forall w\in E,\, [u,v,w] = \left( x \mid w \right)\). D’où la définition :
(Produit vectoriel). Soit \(u\) et \(v\) deux vecteurs. On appelle produit
vectoriel de \(u\) et \(v\) l’unique vecteur noté \(u\wedge v\) vérifiant \(\forall w\in E,\,[u,v,w] =
\left( u\wedge v \mid w \right)\).
Les propriétés du produit mixte permettent d’établir
(Propriétés du produit vectoriel).
Soit \((u,v,w)\in E^3\).
\(u\wedge v = - v\wedge u\) et \(u\wedge u = 0\).
\((u+v)\wedge w = u\wedge w + v\wedge w\).
\(u\wedge v=0\) si et seulement si \((u,v)\) est liée.
ainsi que
(Expression du produit vectoriel dans une
base orthonormale directe). Soit \((i,j,k)\) une base orthonormale
directe de \(E\). on a
\(\bullet\) \(i\wedge j = k\), \(j\wedge k = i\), \(k\wedge i = j\),
et si \(u(x_1,y_1,z_1)\) et \(v(x_2,y_2,z_2)\), alors \(u\wedge v(L,M,N)\) avec
\[L = \begin{vmatrix} y_1 & y_2 \\ z_1 & z_2 \end{vmatrix}, \qquad M = \begin{vmatrix} z_1 & z_2 \\ x_1 & x_2 \end{vmatrix}, \qquad N = \begin{vmatrix} x_1 & x_2 \newline y_1 & y_2 \end{vmatrix}.\]
\(\bullet\) \(i\wedge j = k\), \(j\wedge k = i\), \(k\wedge i = j\),
et si \(u(x_1,y_1,z_1)\) et \(v(x_2,y_2,z_2)\), alors \(u\wedge v(L,M,N)\) avec
\[L = \begin{vmatrix} y_1 & y_2 \\ z_1 & z_2 \end{vmatrix}, \qquad M = \begin{vmatrix} z_1 & z_2 \\ x_1 & x_2 \end{vmatrix}, \qquad N = \begin{vmatrix} x_1 & x_2 \newline y_1 & y_2 \end{vmatrix}.\]
Sous-espaces stables
Soit \(u\) une isométrie de \(E\). Il existe un vecteur non nul \(\varepsilon\in E\) tel que soit \(u\left(\varepsilon\right)=\varepsilon\),
soit \(u\left(\varepsilon\right)=-\varepsilon\).
Intéressons nous au polynôme \(P\left(X\right)=\mathop{\rm det}\left(u-X
\mathop{\mathrm{id}}\nolimits\right)=0\) et montrons que \(1\) ou \(-1\) est une de ses racines. \(P\) est un polynôme à coefficients réels de
degré \(3\) et le coefficient de son
terme dominant est \(-1\). Il vérifie
donc \(\displaystyle{\lim_{X \rightarrow
-\infty}P}=+\infty\) et \(\displaystyle{\lim_{X \rightarrow
+\infty}P}=-\infty\). \(P\) est
de plus continue sur \(\mathbb{R}\).
D’après le théorème des valeurs intermédiaires, \(P\) admet une racine réelle \(\alpha\in\mathbb{R}\). On a alors \(\mathop{\rm det}\left(u-\alpha
\mathop{\mathrm{id}}\nolimits\right)=0\) et \(\operatorname{Ker}\left(u-\alpha
\mathop{\mathrm{id}}\nolimits\right)\) n’est pas réduit au
vecteur nul. Il existe donc un vecteur non nul \(\varepsilon\in E\) tel que \(u\left( \varepsilon\right)= \alpha
\varepsilon\). Mais \(u\) étant
une isométrie, il vient : \(\left\|u\left(\varepsilon\right)\right\|=\left|\alpha\right|\left\|\varepsilon\right\|=\left\|\varepsilon\right\|\)
et donc \(\alpha=\pm
1\). On a ainsi prouvé l’existence d’un vecteur \(\varepsilon\in E\) tel que \(u\left(\varepsilon\right)=\varepsilon\) ou
\(u\left(\varepsilon\right)=-\varepsilon\).
Soit \(u\) une isométrie de \(E\) et soit \(\varepsilon\in E\) un vecteur non nul tel
que \(u\left(\varepsilon\right)=\pm
\varepsilon\). Considérons \(D=Vect\left(\varepsilon\right)\) et soit
\(H\) un supplémentaire orthogonale à
\(D\). Alors :
\(H\) est un plan vectoriel.
\(u\left(H\right)\subset H\).
La restriction du produit scalaire de \(E\) à \(H\) est un produit scalaire sur \(H\) et pour ce produit scalaire, \(u_{|H}\) est une isométrie de \(H\).
Comme \(\dim E=3\), que \(\dim D=1\) et que \(H\) et \(D\) sont supplémentaires dans \(E\), il est clair que \(\dim H=2\).
\(u\) étant une isométrie, elle préserve le produit scalaire et si \(x\in H\) alors \[\left( u\left(x\right) \mid \varepsilon \right)=\pm \left( u\left(x\right) \mid u\left(\varepsilon\right) \right)=\pm\left( x \mid \varepsilon \right)=0\] car \(H\) et \(D\) sont des sous-espaces orthogonaux et \(u\left(H\right)\subset H\).
Il est clair que la restriction du produit scalaire de \(E\) à \(H\) est un produit scalaire sur \(H\). Notons \(\left( \cdot \mid \cdot \right)_{|H}\) ce produit scalaire sur \(H\). Pour tout \(x,y\in H\), on a : \[\left( u_{|H}\left(x\right) \mid u_{|H}\left(y\right) \right)_{|H}=\left( u\left(x\right) \mid u\left(y\right) \right)=\left( x \mid y \right)= \left( x \mid y \right)_{|H}\] et \(u\) est bien une isométrie de \(H\).
Avec les notations des deux
lemmes précédents, considérons \(\varepsilon_3=\dfrac{\varepsilon}{\left\|\varepsilon\right\|}\).
On fixe ainsi une orientation de \(D\)
et on a encore \(u\left(\varepsilon_3\right)=\pm
\varepsilon_3\). Le vecteur \(\varepsilon_3\) induit une orientation du
plan \(H\). Considérons \(\left(\varepsilon_1,\varepsilon_2\right)\)
une base orthonormale directe de \(H\).
La famille \(\left(\varepsilon_1,\varepsilon_2,\varepsilon_3\right)\)
est une base orthonormale directe de l’espace \(E\). Comme \(u_{|H}\) est une isométrie de \(H\), d’après le travail effectué dans le
paragraphe [Etude_gr_orthog_dim_2], on a deux possibilités pour
\(u_{|H}\) :
soit c’une réflexion de \(H\) par rapport à la droite vectorielle \(D_1={\rm Ker}\,\left(u_{|H}-\mathop{\mathrm{id}}\nolimits_H\right)\subset H\) dont un suplémentaire orhogonal dans \(H\) est donné par \(D_2= {\rm Ker}\,\left(u_{|H}+\mathop{\mathrm{id}}\nolimits_H\right)\subset H\). On peut prendre dans ce cas pour \(\varepsilon_1\) un vecteur unitaire qui engendre \(D_1\) et pour \(\varepsilon_2\) un vecteur unitaire qui engendre \(D_2\) en sorte que \(\left(\varepsilon_1,\varepsilon_2\right)\) soit directe.
soit c’est une rotation de \(H\) d’angle \(\theta\in\mathbb{R}\)
On notera \(A\) la matrice de \(u\) dans la base \(\left(\varepsilon_1,\varepsilon_2,\varepsilon_3\right)\) et \(E(1) = \operatorname{Ker}(u - \mathop{\mathrm{id}}\nolimits)\) le sous-espace vectoriel de \(E\) des vecteurs invariants par \(u\).
\(A\) est de la forme \[A=\begin{pmatrix} \cos \theta&-\sin \theta&0 \\\sin\theta &\cos \theta&0\\0&0&1 \end{pmatrix}\] où \(\theta\in \mathbb{R}\) est l’angle de la rotation \(u_{|H}\) du plan orienté \(H\). On dit que \(u\) est une rotation d’angle \(\theta\) et d’axe orienté \(D\). Si \(\theta\neq 0 \left[\pi\right]\), on a : \(E\left(1\right)=D\) et sinon \(u=\mathop{\mathrm{id}}\nolimits\) et \(E\left(1\right)=E\).
Avec les vecteurs \(\varepsilon_2\) et \(\varepsilon_3\) précédemment construits, on a \[A=\begin{pmatrix}1&0&0\\ 0&-1&0\\0&0&1\end{pmatrix}.\] \(u\) est alors une réflexion par rapport au plan \(Vect\left(\varepsilon_1,\varepsilon_3\right)\). De plus \(E\left(1\right)= Vect\left(\varepsilon_1,\varepsilon_3\right)\).
\[A=\begin{pmatrix}\cos \theta&-\sin \theta&0 \\\sin\theta &\cos \theta&0\\0&0&-1 \end{pmatrix}=\begin{pmatrix}1&0&0\\0&1&0\\0&0&-1\end{pmatrix}\begin{pmatrix} \cos \theta&-\sin \theta&0 \\ \sin\theta &\cos \theta&0\\0&0&1 \end{pmatrix}\] et \(u\) est la composée de la reflexion par rapport au plan \(Vect\left(\varepsilon_1,\varepsilon_2\right)\) et d’une rotation. Dans ce cas \(E\left(1\right)=\left\{0\right\}\)
Comme dans le second cas, quitte à bien choisir les vecteurs \(\varepsilon_1\) et \(\varepsilon_2\), la matrice \(A\) est de la forme : \[A=\begin{pmatrix}1&0&0\\0&-1&0\newline0&0&-1 \end{pmatrix}.\] \(u\) est alors une symétrie orthogonale par rapport à la droite \(\mathop{\mathrm{Vect}}\left(\varepsilon_1\right)\). Remarquons que \(u\) est aussi une rotation d’axe \(\mathop{\mathrm{Vect}}\left(\varepsilon_1\right)\) et d’angle \(\pi\). Comme dans le premier cas, \(E\left(1\right)=D\).
Au regard des \(4\) formes précédentes pour la matrice
\(A\), \(u\) est une isométrie directe dans les cas
\(1\) et \(4\) et indirecte dans les cas \(2\) et \(3\).
Isométries directes
(Isométries directes en dimension \(3\) : rotations
vectorielles).
Soit une isométrie directe \(u\in \mathrm{O}_{
}^{+}(E_3)\). On note \(E(1) =
\operatorname{Ker}(u - \mathop{\mathrm{id}}\nolimits)\) le
sous-espace vectoriel formé des vecteurs invariants par \(u\). On a montré que :
Si \(u \neq \mathop{\mathrm{id}}\nolimits_E\), \(E(1)\) est une droite vectorielle \(D = \mathop{\mathrm{Vect}}(\varepsilon_3)\) où \(\varepsilon_3\) est un vecteur de norme \(1\) ;
Pour toute base orthonormée directe \(\varepsilon= (\varepsilon_1, \varepsilon_2, \varepsilon_3)\) (le troisième vecteur \(\varepsilon_3\) dirigeant l’axe et fixé), la matrice de \(u\) dans la base \(\varepsilon\) s’écrit : \[\boxed{Mat_e(u) = \begin{pmatrix} \cos\theta & -\sin\theta&0 \\ \sin\theta & \cos\theta & 0 \newline 0 & 0 & 1 \end{pmatrix}} .\] On dit que \(u\) est la rotation d’axe \(\mathop{\mathrm{Vect}}(e_3)\) et d’angle \(\theta\).
L’angle de la rotation dépend du
choix du vecteur \(d\). Si l’on choisit
\(d' = -d\) pour diriger l’axe,
l’angle \(\theta\) est transformé en
son opposé.
Ne pas confondre l’angle \(\theta\) de la rotation avec l’angle entre
les vecteurs \(x\) et \(r(x)\) !
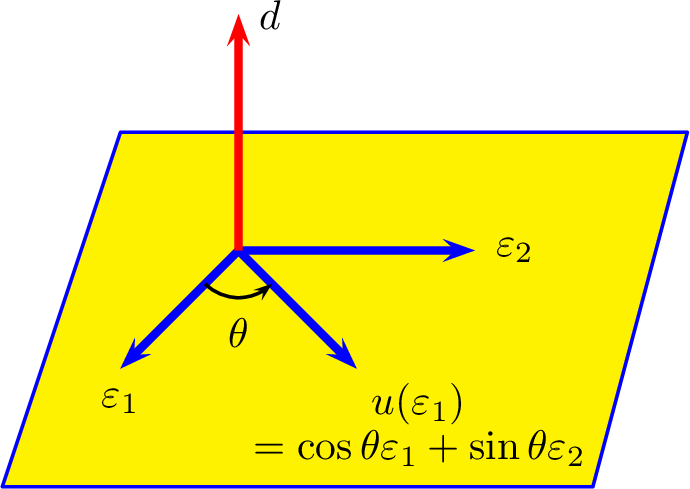
(Détermination de l’angle d’une
rotation). Soient \(E\) un espace
euclidien orienté de dimension \(3\),
\(r\) une rotation et \(\varepsilon\) un vecteur unitaire qui
dirige l’axe de cette rotation. Ce vecteur \(\varepsilon\) définit une orientation du
plan \(H=\mathop{\mathrm{Vect}}{d}^{\perp}\) et
donc de l’angle \(\theta\) de \(r\). Soit \(x \in
H\) : \[\boxed{r(x)=\cos\theta . x +
\sin\theta . \varepsilon\wedge x }.\]
Si \(x=0\) le résultat est évident. Supposons
que \(x\neq 0\). On peut, sans perdre
en généralité, supposer de plus que \(x\) est unitaire. Posons \(y=\varepsilon\wedge x\). \(y\) est un vecteur orthogonal à \(\varepsilon\) et est donc élément de \(H\). La famille \(\left(x,y,\varepsilon\right)\) forme une
base orthonormale directe de \(E\) et
la matrice de \(r\) dans cette base est
\[\begin{pmatrix} \cos\theta &
-\sin\theta&0 \\
\sin\theta & \cos\theta & 0 \newline
0 & 0 & 1 \end{pmatrix}.\] L’image de \(x\) par \(r\) est donc le vecteur : \[r\left(x\right)=\cos \theta . x + \sin \theta .
y= \cos\theta . x + \sin\theta .
\varepsilon\wedge x.\]
Cette proposition donne un moyen
pratique de déterminer les éléments caractéristiques d’une rotation :
(Pour déterminer les éléments
caractéristiques d’une rotation).
Déterminer l’axe \(D\) de la rotation : c’est l’ensemble des vecteurs invariants.
Chercher un vecteur \(d \in D\) unitaire. Il définit une orientation du plan \(P = \mathop{\mathrm{Vect}}(d)^{\perp}\).
Déterminer un vecteur \(\varepsilon_1 \in P\), c’est-à-dire vérifiant \(\left( d \mid \varepsilon_1 \right) = 0\).
Poser \(\varepsilon_2 = d \wedge \varepsilon_1\). Alors \((\varepsilon_1, \varepsilon_2, d)\) est une base orthonormale directe de l’espace.
Calculer \(r(\varepsilon_1)\) et le décomposer sur \(\varepsilon_1\) et \(\varepsilon_2\) : \[r(\varepsilon_1) = \cos\theta \varepsilon_1 + \sin \theta \varepsilon_2\] On en tire \(\cos \theta\) et \(\sin \theta\) et donc l’angle de la rotation.
On peut également utiliser les
remarques suivantes pour étudier une rotation \(u\) donnée par sa matrice \(A\) dans une base quelconque :
(Pour étudier une rotation \(u\) donnée par sa matrice \(A\)).
On vérifie que \(A\in {O}_{3}^{+}(\mathbb{R} )\) en montrant que la matrice \(A\) est orthogonale et que \(\mathop{\rm det}(A)=+1\) (il suffit de comparer \(a_{11}\) et \(\Delta_{11}\)).
On sait que dans toute base orthogonale directe de la forme \(\varepsilon= (\varepsilon_1, \varepsilon_2, d)\), \[Mat_{\varepsilon}(u)=U= \begin{pmatrix} \cos\theta & -\sin\theta&0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}\] Alors les matrices \(A\) et \(U\) sont semblables et par conséquent, \(\mathop{\mathrm{Tr}}(A)=\mathop{\mathrm{Tr}}(U)\) d’où l’on tire \[\boxed{ 2\cos\theta +1 = \mathop{\mathrm{Tr}}(A) }\]
On détermine l’axe de la rotation en cherchant les vecteurs invariants : \(\mathop{\mathrm{Vect}}(d)\) où \(d\) est un vecteur unitaire. Cela revient à résoudre un système homogène \(3 \times 3\).
On détermine un vecteur \(\varepsilon_1\) unitaire orthogonal à \(d\) et on calcule \[\mathop{\mathrm{Det}}\bigl(\varepsilon_1, u(\varepsilon_1), d\bigr)\] Comme ce produit mixte est indépendant de la base orthonormale directe choisie pour le calculer, en introduisant (sans le calculer) \(\varepsilon_2\) tel que \(\varepsilon=(\varepsilon_1,\varepsilon_2,d)\) soit une base orthonormale directe, \[\mathop{\mathrm{Det}}\bigl(\varepsilon_1,u(\varepsilon_1),d\bigr)= \begin{vmatrix} 1 & \cos\theta & 0 \\ 0 & \sin\theta & 0 \newline 0 & 0 & 1 \end{vmatrix} = \sin\theta\]
On obtient donc : \[\boxed{ \cos\theta = \dfrac{\mathop{\mathrm{Tr}}(A)-1}{2} } , \quad \boxed{ \sin\theta = \mathop{\mathrm{Det}}\bigl(\varepsilon_1,u(\varepsilon_1),d\bigr) }\] et l’on en tire l’angle \(\theta\) de la rotation.
Dans l’espace \(\mathbb{R}^{3}\) orienté euclidien usuel,
on considère l’endomorphisme de matrice \[A=\dfrac{1}{2 \sqrt{2}}\begin{pmatrix}
1+\sqrt{2} & -\sqrt{2} & \sqrt{2}-1 \\
\sqrt{2} & 2 & -\sqrt{2} \\
\sqrt{2}-1 & \sqrt{2} & 1+\sqrt{2} \end{pmatrix}\]
dans la base canonique. On va reconnaître cet endomorphisme et préciser
ses éléments caractéristiques. On flaire une isométrie : On calcule la
norme du premier vecteur colonne
\(\dfrac{1}{(2\sqrt2)^2} (1 + 2\sqrt2 + 2 + 2 + 2 - 2\sqrt2 + 1) = 1\). Itou pour le deuxième \({\scriptstyle 1\over\scriptstyle(2\sqrt 2)^2} (2 + 4 + 2) = 1\). Le produit scalaire de ces deux vecteurs colonnes égale \({\scriptstyle 1\over\scriptstyle(2\sqrt 2)^2} ( -\sqrt2 - 2 + 2\sqrt2 + 2 -\sqrt2 ) = 0\). Le produit vectoriel de ces deux vecteurs colonnes a pour coordonnées \({\scriptstyle 2-2(\sqrt 2-1)\over\scriptstyle(2\sqrt 2)^2} = {\scriptstyle 1\over\scriptstyle 2\sqrt 2}\,{\scriptstyle 4-2\sqrt 2\over\scriptstyle 2\sqrt 2} = {\scriptstyle\sqrt 2-1\over\scriptstyle 2\sqrt 2}\) , \({\scriptstyle-(\sqrt 2-1)\sqrt 2 -\sqrt 2(1+\sqrt 2)\over\scriptstyle(2\sqrt 2)^2} = {\scriptstyle 1\over\scriptstyle 2\sqrt 2}\,{\scriptstyle-2+\sqrt 2-\sqrt 2-2\over\scriptstyle 2\sqrt 2} = {\scriptstyle-\sqrt 2\over\scriptstyle 2\sqrt 2}\), \({\scriptstyle 2(1+\sqrt 2)+(\sqrt 2)^2\over\scriptstyle(2\sqrt 2)^2} = {\scriptstyle 1\over\scriptstyle 2\sqrt 2}\, {\scriptstyle 2+2\sqrt 2 + 2\over\scriptstyle 2\sqrt 2}= {\scriptstyle\sqrt 2+1\over\scriptstyle 2\sqrt 2}\).
On retrouve bien le troisième vecteur colonne. On a donc une isométrie positive. C’est donc une rotation d’angle \(\theta\). Comme la trace égale \({\scriptstyle 4+2\sqrt 2\over\scriptstyle 2\sqrt 2} = \sqrt2 + 1 = 1 + 2\cos\theta\). Donc \(\cos\theta = {\scriptstyle\sqrt 2\over\scriptstyle 2}\).
Pour trouver l’axe, on résout le système \(\left\lbrace \begin{array}{rrrrrrrrr} (1+\sqrt{2})&x & -\sqrt{2} &y& +(\sqrt{2}-1) &z& = &2 \sqrt{2}&x \\ \sqrt{2} &x& +2&y & -\sqrt{2}&z&= &2 \sqrt{2}&y\\ (\sqrt{2}-1) &x & +\sqrt{2} &y & (1+\sqrt{2}) &z&= &2 \sqrt{2}&z \end{array}\right.\).
\(\dfrac{1}{(2\sqrt2)^2} (1 + 2\sqrt2 + 2 + 2 + 2 - 2\sqrt2 + 1) = 1\). Itou pour le deuxième \({\scriptstyle 1\over\scriptstyle(2\sqrt 2)^2} (2 + 4 + 2) = 1\). Le produit scalaire de ces deux vecteurs colonnes égale \({\scriptstyle 1\over\scriptstyle(2\sqrt 2)^2} ( -\sqrt2 - 2 + 2\sqrt2 + 2 -\sqrt2 ) = 0\). Le produit vectoriel de ces deux vecteurs colonnes a pour coordonnées \({\scriptstyle 2-2(\sqrt 2-1)\over\scriptstyle(2\sqrt 2)^2} = {\scriptstyle 1\over\scriptstyle 2\sqrt 2}\,{\scriptstyle 4-2\sqrt 2\over\scriptstyle 2\sqrt 2} = {\scriptstyle\sqrt 2-1\over\scriptstyle 2\sqrt 2}\) , \({\scriptstyle-(\sqrt 2-1)\sqrt 2 -\sqrt 2(1+\sqrt 2)\over\scriptstyle(2\sqrt 2)^2} = {\scriptstyle 1\over\scriptstyle 2\sqrt 2}\,{\scriptstyle-2+\sqrt 2-\sqrt 2-2\over\scriptstyle 2\sqrt 2} = {\scriptstyle-\sqrt 2\over\scriptstyle 2\sqrt 2}\), \({\scriptstyle 2(1+\sqrt 2)+(\sqrt 2)^2\over\scriptstyle(2\sqrt 2)^2} = {\scriptstyle 1\over\scriptstyle 2\sqrt 2}\, {\scriptstyle 2+2\sqrt 2 + 2\over\scriptstyle 2\sqrt 2}= {\scriptstyle\sqrt 2+1\over\scriptstyle 2\sqrt 2}\).
On retrouve bien le troisième vecteur colonne. On a donc une isométrie positive. C’est donc une rotation d’angle \(\theta\). Comme la trace égale \({\scriptstyle 4+2\sqrt 2\over\scriptstyle 2\sqrt 2} = \sqrt2 + 1 = 1 + 2\cos\theta\). Donc \(\cos\theta = {\scriptstyle\sqrt 2\over\scriptstyle 2}\).
Pour trouver l’axe, on résout le système \(\left\lbrace \begin{array}{rrrrrrrrr} (1+\sqrt{2})&x & -\sqrt{2} &y& +(\sqrt{2}-1) &z& = &2 \sqrt{2}&x \\ \sqrt{2} &x& +2&y & -\sqrt{2}&z&= &2 \sqrt{2}&y\\ (\sqrt{2}-1) &x & +\sqrt{2} &y & (1+\sqrt{2}) &z&= &2 \sqrt{2}&z \end{array}\right.\).
Soit \(\left\lbrace \begin{array}{rrrrrrr} (1-\sqrt{2})&x & -\sqrt{2} &y& +(\sqrt{2}-1) &z& = 0 \\ \sqrt{2} &x& +(2-2\sqrt2)&y & -\sqrt{2}&z&= 0\\ (\sqrt{2}-1) &x & +\sqrt{2} &y & (1-\sqrt{2}) &z&= 0 \end{array}\right.\). On prend, par exemple, \(d = \left( {\scriptstyle\sqrt 2\over\scriptstyle 2},0,{\scriptstyle\sqrt 2\over\scriptstyle 2}\right)\). Le vecteur \(j(0,1,0)\) lui est orthogonal et appartient donc au plan de rotation. Son image est \(r(j) = \left( -{\scriptstyle 1\over\scriptstyle 2},{\scriptstyle\sqrt 2\over\scriptstyle 2},{\scriptstyle 1\over\scriptstyle 2}\right)\). Enfin \(j\wedge r(j) = ({\scriptstyle 1\over\scriptstyle 2},0,{\scriptstyle 1\over\scriptstyle 2}) = {\scriptstyle\sqrt 2\over\scriptstyle 2} d\). Donc \(\sin\theta d = {\scriptstyle\sqrt 2\over\scriptstyle 2} d\).
Il n’est pas compliqué de
comprendre pourquoi c’est \(\sin\theta
d\) qui est un invariant de la rotation (et pas \(\sin\theta\)). Le vecteur \(d\) oriente le plan de rotation. Pour faire
simple, il donne la direction du "haut". En changeant \(d\) en \(-d\), on intervertit le "haut" et le "bas",
on regarde le plan de l’autre côté, et donc on voit la rotation tourner
"dans l’autre sens". Ceci a pour effet de changer \(\sin\theta\) en son opposé.
Résumons l’étude précédente :
(Classification des isométries en dimension
\(3\)).
Soit un endomorphisme orthogonal \(u \in
\mathrm{O}_{ }(E)\). On note \(E(1) =
\operatorname{Ker}(u - \mathop{\mathrm{id}}\nolimits)\) le
sous-espace formé des vecteurs invariants. Selon la dimension de \(E(1)\), on a la classification suivante :
Dans le dernier cas, \(u = r \circ
s_{H}\), où le plan \(H\)
invariant par la réflexion est orthogonal à l’axe de la rotation \(r\).
| \(\dim E(1)\) | \(\mathop{\rm det}(u)\) | \(u \in\) | Nature de \(u\) |
|---|---|---|---|
| \(3\) | \(1\) | \({O}_{ }^{+}(E)\) | \(\mathop{\mathrm{id}}\nolimits\) |
| \(2\) | \(-1\) | \(\mathrm{O}_{ }^{-}(E)\) | Réflexion \(s_H\) |
| \(1\) | \(1\) | \({O}_{ }^{+}(E)\) | Rotation autour d’un axe \(r\) (dont les demi-tours) |
| \(0\) | \(-1\) | \(\mathrm{O}_{ }^{-}(E)\) | Composée d’une rotation et d’une réflexion |
Si \(A\in
\mathrm{O}_{3}^{-}(\mathbb{R} )\), alors \(\mathop{\rm det}(-A)=-\mathop{\rm
det}(A)=1\). Donc la matrice \(-A\) est spéciale orthogonale. On se ramène
à l’étude précédente. On peut également résumer la classification des
isométries de \(E_3\) de la façon
suivante :
Isométries directes : ce sont des rotations d’axe une droite vectorielle. (Les symétries orthogonales par rapport à une droite sont des rotations d’angle \(\pi\), et on convient que \(\mathop{\mathrm{id}}\nolimits_E\) est une rotation d’angle \(0\)) ;
Isométries indirectes : elles sont de la forme \(-r_{D, \theta}\) où \(r_{D, \theta}\) est une rotation par rapport à une droite vectorielle \(D\) (avec l’identité). On a alors \(u = -r_{D, \theta} = r_{D, \theta + \pi} \circ s_{D^{\perp}}\).
On montre qu’une rotation
vectorielle \(r_{D, \theta}\) s’écrit
comme produit de deux réflexions \(s_{H}\) et \(s_{H'}\) avec \(H\cap H' = D\). Alors toute isométrie
de \(E_3\) se décompose comme un
produit de réflexions. Par conséquent, les réflexions engendrent le
groupe orthogonal \(\mathrm{O}_{
}(E_3)\).
En résumé
Les différentes définitions données dans ce chapitre doivent être connues avec précision. Il ne faut être préçis et rigoureux quand on vérifie qu’une forme bilinéaire est un produit scalaire et il ne faut bien entendu omettre aucun axiome. Il faut de plus parfaitement connaître :
Les inégalités de Schwarz et de Minkowski.
Le théorème de Pythagore.
La notion de base orthogo(nor)nale et Le procédé d’orthonormalisation de Schmidt.
Les notions de sous-espaces orthogonaux, de projections et de symétries orthogonales.
Bibliographie
Barre utilisateur
[ID: 80] [Date de publication: 5 janvier 2022 23:01] [Catégorie(s): Le cours de SUP ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]Commentaires sur le cours
Documents à télécharger
L'article complet