Lecture zen
Introduction au calcul différentiel dans le cas particulier des fonctions de deux variables réelles.
Calcul différentiel
Introduction au calcul différentiel dans le cas particulier des fonctions de deux variables réelles.
Pour bien aborder ce chapitre
Ce chapitre a pour vocation de servir d’introduction aux fonctions de plusieurs variables. Ces fonctions sont bien évidemment importantes que ce soit en maths ou en physique. Un phénomène physique en particulier dépend souvent de plusieurs paramètres. Nous nous cantonnerons ici aux fonctions de deux variables réelles à valeurs dans \(\mathbb{R}\). Vous étudierez le cas général en deuxième année dans le cadre des espaces vectoriels normés. Vous verrez alors que tout a déjà été dit ou presque dans le cas simplifié qui va nous occuper ici.
On verra que l’on transpose facilement les notions de limite et de continuité aux fonctions de deux variables. Il n’en est malheureusement pas de même pour la notion de dérivée. Ainsi, le taux d’accroissement pour une fonction \(f:I\subset \mathbb{R}\rightarrow \mathbb{R}\) en un point \(a\in I\) est donné par : \[\dfrac{f\left(x\right)-f\left(a\right)}{x-a},\quad x\in I\setminus\left\{a\right\} .\] La même quantité n’a pas de sens pour les fonctions de deux variables car \(x\) et \(a\) sont dans ce cas des vecteurs de \(\mathbb{R}^2\).
C’est à ce niveau que va intervenir la notion de différentielle et qu’un pont va être posé entre l’analyse et l’algèbre linéaire. Plutôt que de chercher à définir une dérivée, on va approximer la fonction étudiée par une application linéaire.
On verra qu’alors la théorie sera très proche de celle que vous connaissez pour les fonctions d’une variable réelle. En particulier, on pourra écrire une inégalité des accroissements finis et une formule de Taylor-Young pour les fonctions de deux variables.
Nous terminerons ce chapitre par quelques éléments sur les équations aux dérivées partielles. Elles sont aux fonctions de plusieurs variables ce que les équations différentielles sont aux fonctions d’une seule. Elles sont aussi évidemment très importantes en physique.
Dans tout ce chapitre, \(\mathbb{R}^2\) est muni de la norme euclidienne usuelle : \(\forall \left(x,y\right)\in\mathbb{R}^2,\quad \left\|\left(x,y\right)\right\|=\sqrt{x^2+y^2}\).
Continuité des fonctions à deux variables
(Boule ouverte). On appelle boule ouverte de centre \(M_0\in\mathbb{R}^2\) et de rayon \(r>0\) le sous-ensemble de \(\mathbb{R}^2\) noté \(B\left(M_0,r\right)\) défini par : \[B\left(M_0,r\right)=\left\{M\in\mathbb{R}^2 ~|~ \left\|M-M_0\right\|<r \right\}.\]
(Partie ouverte). On dit que \(U\subset \mathbb{R}^2\) est une partie ouverte de \(\mathbb{R}^2\) si pour tout point \(M_0\in U\) il existe \(r>0\) tel que la boule ouverte de centre \(M_0\) et de rayon \(r\) soit incluse dans \(U\).
(Voisinage d’un point). Soit \(M_0 \in \mathbb{R} [2]\). On dit qu’une partie \(V \subset \mathbb{R} [2]\) est un voisinage du point \(M_0\) s’il existe \(r > 0\) tel que la boule ouverte de centre \(M_0\) et de rayon \(r\) soit incluse dans \(V\). Avec ce vocabulaire, une partie \(U\) est ouverte si et seulement si \(U\) est un voisinage de chacun de ses points.
On s’intéresse dans ce chapitre aux fonctions \(f\) définies sur une partie ouverte \(U\subset \mathbb{R}^2\) et à valeurs réelles : \[\left\{ \begin{array}{ccl} U \subset \mathbb{R} [2] & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto & f(x,y) \end{array} \right.\] On peut représenter le graphe d’une telle fonction : en tout point \((x,y) \in U\), on associe une hauteur \(z = f(x,y)\) et lorsque \((x,y)\) varie dans \(U\), on décrit une surface de \(\mathbb{R} [3]\) de base l’ouvert \(U\) : \[G = \{(x,y,z) \in \mathbb{R} [3] \mid (x,y) \in U,~ z = f(x,y)\}\] Pour un point \((x_0, y_0) \in U\), comme \(U\) est ouvert, il existe \(\alpha > 0\) tel que \(\forall u \in ]-\alpha, \alpha[\), \((x_0 + u, y_0) \in U\) et \((x_0, y_0 + u) \in U\). On peut donc définir deux fonctions d’une variable \(f_1\) (définie sur un voisinage de \(x_0\)) et \(f_2\) (définie sur un voisinage de \(y_0\)) appelées applications partielles de \(f\) au point \((x_0, y_0)\) : \[f_1 : \left\{ \begin{array}{ccl} ]x_0-\alpha, x_0+\alpha[ & \longrightarrow & \mathbb{R} \\ t & \longmapsto & f(t, y_0) \end{array} \right. \quad f_2 : \left\{ \begin{array}{ccl} ]y_0-\alpha, y_0+\alpha[ & \longrightarrow & \mathbb{R} \newline t & \longmapsto & f(x_0, t) \end{array} \right.\]
[Applications partielles en \(M_0\)]
(Limite en un point). Soient \(U\subset \mathbb{R}^2\) une partie ouverte, \(M_0=(x_0, y_0)\in U\) et \(f:U\mapsto \mathbb{R}\). On dit que \(f\) tend vers \(l\in\mathbb{R}\) quand \(M=(x,y)\) tend vers \(M_0\) si et seulement si : \[\forall
\varepsilon>0,\quad \exists \eta>0,\quad \forall x\in U,\quad
\left\|M-M_0\right\|\leqslant\eta \Rightarrow \lvert f(M)-l \rvert \leqslant\varepsilon\] On note alors \(f\left(M\right)\xrightarrow[M\rightarrow M_0]{}l\).
Si \(f\) admet une limite quand \(M\) tend vers \(M_0\) alors cette limite est unique.
(Continuité en un point). Soit \(U \subset \mathbb{R} [2]\) un ouvert, \(M_0\in U\) et \(f : U \mapsto \mathbb{R}\). On dit que \(f\) est continue en \(M_0\) si et seulement si \[f\left(M\right)\xrightarrow[M\rightarrow M_0]{} f\left(M_0\right)\]
(Théorème de majoration). Soit \(U \subset \mathbb{R} [2]\) un ouvert, \(M_0\in U\), \(l \in\mathbb{R}\), \(f : U
\mapsto \mathbb{R}\) et \(\theta:\mathbb{R}\rightarrow \mathbb{R}\) tels que, au voisinage de \(M_0\) on ait :
alors : \(f\left(M\right)\xrightarrow[M\rightarrow M_0]{} l\).
\(\left|f\left(M\right)-l\right|\leqslant\theta\left(\left\|M-M_0\right\|\right)\)
\(\theta\left(t\right)\xrightarrow[t\rightarrow 0]{} 0\)
Soit \(\varepsilon> 0\). Puisque \(\theta(t) \xrightarrow[t \rightarrow 0]{} 0\), il existe \(\eta
> 0\) tel que \(\forall t \in ]-\eta, \eta[\), \(\lvert \theta(t) \rvert \leqslant
\varepsilon\). Soit \(M \in U\) tel que \(\lVert M-M_0 \rVert_{ } \leqslant\eta\), on a \[\lvert f(M) - l \rvert \leqslant\theta(\lVert M-M_0 \rVert_{ }) \leqslant\varepsilon\]
Pour montrer en pratique qu’une fonction de deux variables admet une limite en \(M_0=(x_0,y_0)\), on utilise les coordonnées polaires de pôle \(M_0\). Pour \(M=(x,y)\in U\), en écrivant \[\begin{cases} x &= x_0 + r\cos \theta \newline y &= y_0 + r\sin \theta \end{cases}\] on a \(r = \lVert M - M_0 \rVert_{ }\) et il suffit alors de majorer \(\lvert f(M)-f(M_0) \rvert\) par une fonction qui ne dépend que de \(r\), \(\theta(r)\) avec \(\theta(r) \xrightarrow[r \rightarrow 0]{} 0\).
Étudier la limite lorsque \((x,y) \rightarrow (0,0)\) de la fonction définie sur \(\mathbb{R} [2] \setminus \{(0,0)\}\) par \[f(x,y) = \dfrac{x^3y}{x^2+y^2}\] Introduisons des coordonnées polaires \(x = r\cos \theta\), \(y = r\sin
\theta\), \[\lvert f(x,y) \rvert = r \cos^2 \theta \lvert \sin \theta \rvert \leqslant r\] Par conséquent, \(f(x,y) \xrightarrow[(x,y) \rightarrow (0,0)]{} 0\).
Même question pour \(f(x,y) = \dfrac{x^3y^2}{x^4+y^4}\). Avec les coordonnées polaires, \[\lvert f(x,y) \rvert = r \dfrac{\lvert \cos \theta \rvert ^3 \sin^2
\theta}{\cos^4\theta + \sin^4 \theta} \leqslant\dfrac{r}{\cos^4 \theta
+ \sin^4 \theta}\] Comme la fonction \(\varphi: \theta \mapsto \cos^4\theta +
\sin^4\theta\) est continue sur le segment \([0, 2\pi]\), elle possède un minimum qui est strictement positif (le cosinus et le sinus ne peuvent s’annuler simultanément) : \(\forall \theta \in [0, 2\pi]\), \(\cos^4\theta + \sin^4 \theta \geqslant\alpha > 0\) et alors \(\lvert f(x,y) \rvert \leqslant r/\alpha\) ce qui montre que \(f(x,y)
\xrightarrow[(x,y) \rightarrow (0,0)]{} 0\).
(Caractérisation séquentielle de la limite). Si \(f(M) \xrightarrow[M \rightarrow M_0]{} l\), alors pour toute suite \(M_n=(x_n, y_n)\) vérifiant \(\lVert M_n-M_0 \rVert_{ } \xrightarrow[n \rightarrow +\infty]{}0\) (on note \(M_n
\xrightarrow[n \rightarrow +\infty]{}M_0\)), on a \(f(M_n) \xrightarrow[n \rightarrow +\infty]{}l\).
Soit \(\varepsilon> 0\). Comme \(f(M) \xrightarrow[M \rightarrow M_0]{}\), il existe \(\eta > 0\) tel que \(\forall M \in U\), \(\lVert M-M_0 \rVert_{ } \leqslant\eta \Rightarrow
\lvert f(M) - l \rvert \leqslant\varepsilon\). Puisque \(M_n \xrightarrow[n \rightarrow +\infty]{}M_0\), il existe \(N \in
\mathbb N\) tel que \(\forall n \geqslant N\), \(\lVert M_n-M_0 \rVert_{ } \leqslant\eta\). Alors pour \(n \geqslant N\), \(\lvert f(M_n) - l \rvert \leqslant\varepsilon\).
On se sert souvent de cette propriété séquentielle pour montrer qu’une fonction n’a pas de limite.
Étudier l’existence d’une limite en \((0,0)\) de la fonction définie par \(f(x,y) = \dfrac{xy}{x^2+y^2}\). Avec les coordonnées polaires à l’origine, \(f(x,y) =
\dfrac{\sin(2\theta)}{2}\). On voit que les valeurs que prend \(f\) dépendent de l’angle \(\theta\) selon lequel on s’approche de l’origine. Montrons que \(f\) n’a pas de limite en \((0,0)\) en exhibant deux suites : \(X_n = (1/n, 0)\) et \(Y_n=(1/n,1/n)\). Si \(f\) admettait une limite \(l \in \mathbb{R}\) lorsque \((x,y) \xrightarrow[n \rightarrow +\infty]{}0\), alors comme \(X_n
\xrightarrow[n \rightarrow +\infty]{}(0,0)\) et \(Y_n \xrightarrow[n \rightarrow +\infty]{}(0, 0)\), on aurait \(f(X_n) \xrightarrow[n \rightarrow +\infty]{}l\) et \(f(Y_n) \xrightarrow[n \rightarrow +\infty]{}l\) mais \(\forall n \in \mathbb N[\star]\), \(f(X_n) = 0\) et \(f(Y_n)= 1/2\). On devrait avoir \(l = 0 = 1/2\), une absurdité.
(Continuité des applications partielles). Si \(f\) est continue au point \(M_0=(x_0,y_0)\), alors les deux applications partielles au point \(M_0\), \(f_1\) et \(f_2\) sont continues respectivement en \(x_0\) et \(y_0\).
Soit \(\varepsilon> 0\). Comme \(U\) est ouvert, les deux applications partielles \(f_1\) et \(f_2\) sont définies respectivement sur un voisinage de \(x_0\), \(f_1 : ]x_0-\alpha, x_0+\alpha[ \mapsto \mathbb{R}\) et sur un voisinage de \(y_0\) : \(f_2 : ]y_0-\alpha, y_0+\alpha[ \mapsto
\mathbb{R}\). Puisque \(f\) est continue au point \(M_0=(x_0,y_0)\), il existe \(0 < \eta \leqslant\alpha\) tel que \(\forall M \in U\), \(\lVert M-M_0 \rVert_{ } \leqslant\eta
\Rightarrow \lvert f(M)-f(M_0) \rvert \leqslant\varepsilon\). Soit alors \(x \in
]x_0-\alpha,x_0+\alpha[\) vérifiant \(\lvert x - x_0 \rvert \leqslant\eta\). Posons \(M = (x, y_0)\), \(\lVert M-M_0 \rVert_{ } = \lvert x-x_0 \rvert \leqslant\eta\) d’où \[\lvert f_1(x)-f_1(x_0) \rvert = \lvert f(x,y_0) - f(x_0,y_0) \rvert \leqslant\varepsilon\] De même, puisque \(\lVert (x_0, y) - (x_0,y_0) \rVert_{ } = \lvert y-y_0 \rvert \leqslant
\eta\), \[\lvert f_2(y) - f_2(y_0) \rvert = \lvert f(x_0,y)-f(x_0,y_0) \rvert \leqslant\varepsilon\]
Il est important de comprendre que la réciproque de ce résultat est fausse comme le montre l’exemple suivant :
\[f : \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto & \begin{cases}
\dfrac{xy}{x^2+y^2} \textrm{ si } (x,y) \neq (0, 0) \newline
0 & \textrm{ si } (x,y) = (0, 0)
\end{cases}
\end{array} \right.\] Les deux applications partielles en \((0,0)\) sont définies par \(f_1(x) = f(x,0) =
0\) et \(f_2(y) = f(0, y) = 0\). Ces deux fonctions sont continues alors qu’on a vu précédemment que \(f\) n’admettait pas de limite à l’origine.
Il se peut qu’une fonction admette un limite à l’origine dans toutes les directions sans qu’elle soit continue comme le montre l’exemple suivant : \[f : \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto &
\begin{cases}
\dfrac{xy^6}{x^6 + y^8} & \textrm{ si } (x,y) \neq (0, 0) \\
0 & \textrm{ si } (x,y) = (0, 0)
\end{cases}
\end{array} \right.\] Considérons la restriction de \(f\) à une droite d’équation \(y =
\alpha x\) : \[f_{\alpha} : \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \\ x & \longmapsto &
f(x, \alpha x) =
\begin{cases}
\dfrac{\alpha^6 x}{1 + \alpha^8 x^2} & \textrm{ si } x \neq 0 \newline
0 & \textrm{ si } x = 0
\end{cases}
\end{array} \right.\] On a bien \(f_{\alpha}(x) \xrightarrow[x \rightarrow 0]{} 0 = f_{\alpha}(0)\) ce qui montre que toutes les applications \(f_{\alpha}\) sont continues en \(0\), mais la fonction \(f\) n’admet pas de limite en \((0,0)\). En effet, si l’on s’approche de l’origine suivant la parabole d’équation \(x = y^2\) avec la suite \(M_n = (1/n^2, 1/n)\), \[f(M_n) = \dfrac{1}{1+1/n^4} \xrightarrow[n \rightarrow +\infty]{}1 \neq f(0,0)\]
Multimédia: animation pour illustrer cet exemple, sur un graphe on voit la coupe par un plan qui tourne, une bosse qui tend vers \(0\) et la parabole mise en évidence
(Composée de fonctions continues). On considère une fonction \[f : \left\{ \begin{array}{ccl} U & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto & f(x,y) \end{array} \right.\] continue au point \((x_0, y_0) \in U\) et une fonction \[\varphi: \left\{ \begin{array}{ccl} V\subset \mathbb{R} [2] & \longrightarrow & U \\ (u,v) & \longmapsto & (x(u,v), y(u,v)) \end{array} \right.\] On suppose que les deux fonctions \(x : V \mapsto \mathbb{R}\) et \(y : V \mapsto
\mathbb{R}\) sont continues au point \((u_0, v_0)\). Alors la composée : \[F : \left\{ \begin{array}{ccl} V & \longrightarrow & \mathbb{R} \newline (u,v) & \longmapsto & f(x(u,v), y(u,v)) \end{array} \right.\] est continue au point \((u_0, v_0)\).
Il suffit d’écrire les définitions de continuité.
Si \(f : U \subset \mathbb{R} [2] \mapsto \mathbb{R}\) est continue et \(x, y :
I\subset \mathbb{R} \mapsto \mathbb{R}\) sont deux fonctions continues sur \(I\) vérifiant \(\forall t \in I\), \((x(t), y(t)) \in U\), la composée \[\varphi: \left\{ \begin{array}{ccl} I & \longrightarrow & \mathbb{R} \newline t & \longmapsto & f(x(t),y(t)) \end{array} \right.\] est continue en tout point de \(I\).
Dérivées partielles, fonctions \(\mathcal{C}^{1}\)
Soit \(U\subset \mathbb{R}^2\) un ouvert de \(\mathbb{R}^2\).
(Dérivée selon un vecteur). Soit \(f: U \mapsto \mathbb{R}\), \(M_0 \in U\) et un vecteur non nul \(\overrightarrow{H} \in \mathbb{R}^2\). On dit que \(f\) possède une dérivée au point \(M_0\) selon le vecteur \(\overrightarrow{H}\) s’il existe un réel \(l \in \mathbb{R}\) tel que \[\dfrac{1}{t}\bigl[f(M_0+t.\overrightarrow{H}) - f(M_0)\bigr] \xrightarrow[t \rightarrow 0]{} l\] On note alors \(l = {\mathrm{D}_{\overrightarrow{H}}}f(M_0)\).
Pour la fonction \[f : \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto &
\begin{cases}
\dfrac{x^2y}{x^2+y^2} & \textrm{ si } (x,y) \neq (0,0) \newline
0 & \textrm{ si } (x, y) = 0
\end{cases}
\end{array} \right.\] On considère un vecteur \(\overrightarrow{H}=(h,k) \in \mathbb{R} [2]\). Formons le taux d’accroissement \[\dfrac{1}{t} \bigl[ f(th, tk) - f(0,0) \bigr] =
\dfrac{h^2k}{h^2+k^2}
\xrightarrow[t \rightarrow 0]{} \dfrac{h^2k}{h^2+k^2}\] ce qui montre que \(f\) possède une dérivée selon le vecteur \(\overrightarrow{H}\) en \((0,0)\) et \({\mathrm{D}_{\overrightarrow{H}}}f(0,0) = \dfrac{h^2k}{h^2+k^2}\).
Multimédia: Coupe de la surface par un plan qu’on fait tourner et représenter le graphe de la fonction partielle avec la pente de la tangente
(Dérivées partielles en un point). Soit \(f : U \mapsto \mathbb{R}\) et \(a \in U\). On considère la base canonique \(e = (e_1,e_2)\) de \(\mathbb{R}^2\). On appelle dérivées partielles de \(f\) au point \(M_0 \in U\) les dérivées de \(f\), si elles existent, selon les vecteurs \(e_1\) et \(e_2\) et on note alors \[\boxed{
\dfrac{\partial f}{\partial x}(M_0) =
D_{e_1}f(M_0) =
\lim_{t \rightarrow 0} \dfrac{f(M_0+te_1)-
f(M_0)}{t}
}\quad \textrm{ et} \quad\boxed{
\dfrac{\partial f}{\partial y}(M_0) =
D_{e_2}f(M_0) =
\lim_{t \rightarrow 0} \dfrac{f(M_0+te_2)-
f(M_0)}{t}
}\]
En notant \(f_1\) et \(f_2\) les applications partielles au point \(M_0=(x_0,y_0)\), \[\begin{cases}
\dfrac{\partial f}{\partial x}(x_0,y_0) &= \lim_{t\rightarrow 0} \dfrac{f(x_0+t, y_0)
- f(x_0,y_0)}{t} =\lim_{t\rightarrow 0} \dfrac{f_1\left(x_0+t\right)-f_1\left(x_0\right)}{t} \\[0.4cm]
\dfrac{\partial f}{\partial y}(x_0,y_0) &= \lim_{t \rightarrow 0} \dfrac{f(x_0, y_0+t)
- f(x_0,y_0)}{t} =\lim_{t\rightarrow 0} \dfrac{f_2\left(y_0+t\right)-f_2\left(y_0\right)}{t}
\end{cases}\] Ces limites existent si et seulement si \(f_1\) et \(f_2\) sont dérivables respectivement en \(x_0\) et \(y_0\). De plus, dans ce cas :
On retient la règle de calcul suivante : pour calculer \(\dfrac{\partial f}{\partial x}(x,y)\), on gèle la variable \(y\) (considérée comme constante) et on dérive par rapport à \(x\). De même, pour calculer \(\dfrac{\partial f}{\partial y}(x,y)\), on fixe \(x\) et on dérive l’expression par rapport à \(y\).
\[\begin{cases} \dfrac{\partial f}{\partial x}(x_0,y_0) &= f'_1\left(x_0\right)\newline[0.4cm] \dfrac{\partial f}{\partial y}(x_0,y_0)&=f'_2\left(y_0\right) \end{cases}\] Par exemple, si \(f(x,y) = x^2 \cos(y)\), pour calculer en un point \((x,y)\) \(\dfrac{\partial f}{\partial x}\), on fixe la variable \(y\), la première fonction partielle en \((x,y)\) est définie par \(f_1(t) = f(t,y) = t^2\cos(y)\), elle est dérivable en \(t=x\) et \(\dfrac{\partial f}{\partial x}(x,y) = f_1'(x) = 2x\cos(y)\). La deuxième fonction partielle en \((x,y)\) est définie par \(f_2(t) = f(x,t) = x^2\cos(t)\), elle est dérivable en \(t=y\) et \(\dfrac{\partial f}{\partial y}(x,y) = f_2'(y) = -x^2\sin(y)\).
Considérons la fonction définie sur \(\mathbb{R} [2]\) par \[f(x,y) =
\begin{cases}
x^4 & \textrm{ si } y \leqslant x^2 \\
y^2 & \textrm{ si } y > x^2
\end{cases}\]
Étudions l’existence de dérivées partielles de \(f\) en un point \(M_0=(x_0,y_0)\).
Si \(y_0 < x_0^2\), sur un voisinage de \(M_0\), la fonction \(f\) est définie par \(f(x,y) = x^2\). On peut appliquer la règle de calcul ci-dessus, \(\dfrac{\partial f}{\partial x}(x_0,y_0) = 2x_0\) et \(\dfrac{\partial f}{\partial y}(x_0,y_0) = 0\).
Si \(y_0 > x_0^2\), sur un voisinage de \(M_0\), \(f(x,y) = y^2\) donc \(\dfrac{\partial f}{\partial x}(x_0,y_0) = 0\) et \(\dfrac{\partial f}{\partial y}(x_0,y_0) = 2y_0\).
Si \(M_0=(x_0, x_0^2)\) avec \(x_0>0\), on se trouve sur un point de la parabole et les applications partielles sont définies par : \[f_1 : \left\{ \begin{array}{ccl} ]0, +\infty[ & \longrightarrow & \mathbb{R} \\ t & \longmapsto & \begin{cases} y_0^2 & \textrm{ si } t < x_0 \\ t^4 & \textrm{ si } t \geqslant x_0 \end{cases} \end{array} \right. \quad f_2 : \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \\ t & \longmapsto & \begin{cases} x_0^4 & \textrm{ si } t < y_0 \\ t^2 & \textrm{ si } t \geqslant y_0 \end{cases} \end{array} \right.\] La fonction \(f_1\) est dérivable à droite en \(x_0\), avec \(f_{1d}'(x_0) =4x_0^3\). Elle est dérivable à gauche en \(x_0\) avec \(f_{1g}'(x_0) = 0\). On en déduit que \(f_1\) n’est pas dérivable en \(x_0\) donc que \(\dfrac{\partial f}{\partial x}(x_0,x_0^2)\) n’existe pas. De la même façon, \(\dfrac{\partial f}{\partial y}(x_0, x_0^2)\) n’existe pas.
Si \(M_0 = (0,0)\), les deux fonctions partielles en \((0,0)\) sont définies par \[f_1(t) = t^4, \quad f_2(t) = \begin{cases} 0 & \textrm{ si } t \leqslant 0 \newline t^2 & \textrm{ si } t > 0 \end{cases}\] Puisque ces fonctions sont dérivables en \(0\), on en tire que \(\dfrac{\partial f}{\partial x}(0,0) = \dfrac{\partial f}{\partial y}(0,0) = 0\).
(Fonction de classe \(\mathcal{C}^{1}\)). Soit \(f : U\subset \mathbb{R}^2 \mapsto \mathbb{R}\). On dit que la fonction \(f\) est de classe \(\mathcal{C}^{1}\) sur l’ouvert \(U\) lorsque :
En tout point \((x,y) \in U\), \(f\) possède des dérivées partielles \(\dfrac{\partial f}{\partial x}(x,y)\) et \(\dfrac{\partial f}{\partial y}(x,y)\).
Chacune des fonctions \[\dfrac{\partial f}{\partial x} : \left\{ \begin{array}{ccl} U & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto & \dfrac{\partial f}{\partial x}(x,y) \end{array} \right. \quad \textrm{ et} \quad \dfrac{\partial f}{\partial y} : \left\{ \begin{array}{ccl} U & \longrightarrow & \mathbb{R} \newline (x,y) & \longmapsto & \dfrac{\partial f}{\partial y}(x,y) \end{array} \right.\] est continue sur \(U\).
Considérons la fonction définie par \[f : \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto &
\begin{cases}
\dfrac{\sin(x^3)-\sin(y^3)}{x^2+y^2} & \textrm{ si } (x,y) \neq
(0,0) \\
0 & \textrm{ si } (x,y) = (0, 0)
\end{cases}
\end{array} \right.\] Soit \(M_0= (x_0, y_0) \in \mathbb{R} [2]\). Étudions l’existence de dérivées partielles en \(M_0\).
Si \((x_0,y_0) \neq (0, 0)\), sur un voisinage de \(M_0\), la première application partielle \(f_1\) en \(M_0\) est définie par \[f_1(t) = \dfrac{\sin(t^3) - \sin(y_0^3)}{t^2+y_0^2}\] Elle est dérivable en \(x_0\) et \(f_1'(x_0) = \dfrac{\partial f}{\partial x}(x_0,y_0)= \dfrac{3x_0^2\cos(x_0^3)}{x_0^2 + y_0^2} - 2x_0 \dfrac{\sin(x_0^3)-\sin(y_0^3)}{(x_0^2+y_0^2)^2}\) On calcule de même \(\dfrac{\partial f}{\partial y}(x_0,y_0)\).
Si \((x_0, y_0) = (0, 0)\), revenons à la définition de \(\dfrac{\partial f}{\partial x}(0,0)\) et formons le taux d’accroissement \[\dfrac{f(t,0)-f(0,0)}{t} = \dfrac{\sin(t^3)}{t^3} \xrightarrow[t \rightarrow 0]{} 1\] ce qui montre que \(\dfrac{\partial f}{\partial x}(0,0)\) existe et vaut \(1\). De même, \(\dfrac{\partial f}{\partial y}(0,0) = -1\).
(Théorème d’opérations sur les fonctions de classe \(\mathcal{C}^{1}\).). Soient \(f\) et \(g\) deux fonctions définies sur un ouvert \(U \subset
\mathbb{R}^2\) à valeurs réelles et de classe \(\mathcal{C}^{1}\) sur \(U\). Alors :
si \(\alpha,\beta\in\mathbb{R}\), \(\alpha f + \beta g\) est de classe \(\mathcal{C}^{1}\) sur \(U\) et : \[\forall i=1,2,\quad \boxed{\dfrac{\partial \left(\alpha f + \beta g\right)}{\partial x_i}=\alpha \dfrac{\partial f}{\partial x_i} + \beta \dfrac{\partial g}{\partial x_i}}\]
\(fg\) est de classe \(\mathcal{C}^{1}\) sur \(U\) et : \[\forall i=1,2,\quad \boxed{\dfrac{\partial \left(fg\right)}{\partial x_i}= g\dfrac{\partial f}{\partial x_i} + f \dfrac{\partial g}{\partial x_i}}\]
si \(g\) ne s’annule pas sur \(U\) alors \({\scriptstyle f\over\scriptstyle g}\) est définie et \(\mathcal{C}^{1}\) sur \(U\). De plus : \[\forall i=1,2,\quad \boxed{\dfrac{\partial \left({\scriptstyle f\over\scriptstyle g}\right)}{\partial x_i}={\scriptstyle g\dfrac{\partial f}{\partial x_i} - f \dfrac{\partial g}{\partial x_i}\over\scriptstyle g^2}}\]
\(\left(\mathcal{C}^{1}\left(U,\mathbb{R}\right),+,.\right)\) est un sous-espace vectoriel de \(\mathscr F \left(U,\mathbb{R}\right)\)
\(\left(\mathcal{C}^{1}\left(U,\mathbb{R}\right),+,\times\right)\) est un sous-anneau de \(\mathscr F \left(U,\mathbb{R}\right)\)
Le théorème suivant (la démonstration est admise) est le résultat fondamental de ce chapitre :
(Dl d’ordre \(1\)). Soit \(f : U\subset \mathbb{R}^2 \mapsto \mathbb{R}\) de classe \(\mathcal{C}^{1}\) sur l’ouvert \(U\) et \(M_0=(x_0,y_0) \in U\). Alors il existe une fonction \(\varepsilon: V \subset
\mathbb{R}^2 \rightarrow \mathbb{R}\) définie sur un voisinage \(V\) de \(\left(0,0\right)\) telle que :
On dit alors que \(f\) admet un développement limité d’ordre \(1\) en \(M_0\).
Pour tout accroissement \(\overrightarrow{H} = (h,k)\in \mathbb{R}^2\) tel que \(M_0+\overrightarrow{H} \in U\), on a : \[\boxed{f(x_0+h, y_0+k) = f(x_0,y_0) +h \dfrac{\partial f}{\partial x}(x_0,y_0) + k\dfrac{\partial f}{\partial y}(x_0,y_0) + \left\|(h,k)\right\|\varepsilon(h,k) }\]
\(\varepsilon(h,k)\xrightarrow[(h,k)\rightarrow (0,0)]{}0\)
La définition de \(f\) de classe \(\mathcal{C}^{1}\) ne suppose pas que \(f\) est continue sur \(U\). C’est une conséquence du résultat suivant :
(Une fonction \(\mathcal{C}^{1}\) est continue). Si \(f\) est de classe \(\mathcal{C}^{1}\) sur \(U\) alors \(f\) est continue en tout point de \(U\).
Soit \(M_0=(x_0,y_0) \in U\) et \(M = (x,y)\). Notons \(\overrightarrow{H}=M-M_0=(x-x_0,y-y_0)\). Puisque \(f\) est de classe \(\mathcal{C}^{1}\) sur \(U\), il existe \(\varepsilon\) définie sur un voisinage de \((0,0)\) telle que \(f(x,y) = f(x_0,y_0) + (x-x_0)\dfrac{\partial f}{\partial x}(x_0,y_0) +
(y-y_0)\dfrac{\partial f}{\partial y}(x_0, y_0) + \lVert M-M_0 \rVert_{ }\varepsilon(x-x_0, y-y_0)\) avec \(\varepsilon(h, k) \xrightarrow[(h,k) \rightarrow (0,0)]{} 0\). La fonction \(\varepsilon\) est bornée sur un voisinage de \((0, 0)\) donc si \(\lVert M-M_0 \rVert_{ } \leqslant\eta\), \(\lvert \varepsilon(M-M_0) \rvert \leqslant K\) et comme \(\lvert x-x_0 \rvert \leqslant\lVert M-M_0 \rVert_{ }\), \(\lvert y-y_0 \rvert \leqslant\lVert M-M_0 \rVert_{ }\), \(\lvert f(x,y)-f(x_0,y_0) \rvert \leqslant\lvert x-x_0 \rvert \lvert \dfrac{\partial f}{\partial x}(x_0,y_0) \rvert +
\lvert y-y_0 \rvert \lvert \dfrac{\partial f}{\partial y}(x_0,y_0) \rvert + K\lVert M-M_0 \rVert_{ } \leqslant
C\lVert M-M_0 \rVert_{ }\). Par conséquent, \(f(x,y) \xrightarrow[(x,y) \rightarrow (x_0,y_0)]{} f(x_0,y_0)\).
Plus intéressant, si \(f\) admet des dérivées dans les deux directions de la base canonique, elle admet une dérivée dans toutes les directions qui se calcule comme combinaison linéaire des dérivées partielles comme le précise le résultat suivant :
(Une fonction \(\mathcal{C}^{1}\) admet des dérivées selon tout vecteur). Si \(f : U \mapsto \mathbb{R}\) est de classe \(\mathcal{C}^{1}\) sur l’ouvert \(U\), alors pour tout point \(M_0=(x_0,y_0)\) et tout vecteur non nul \(\overrightarrow{H}=(h,k)\), \(f\) admet une dérivée selon le vecteur \(\overrightarrow{H}\) au point \(M_0\) et \[{\mathrm{D}_{\overrightarrow{H}}}{f}(M_0) = h\dfrac{\partial f}{\partial x}(x_0,y_0) + k
\dfrac{\partial f}{\partial y}(x_0,y_0)\]
Avec le DL à l’ordre \(1\), le taux d’accroissement s’écrit : \(\dfrac{1}{t}\bigl[f(x_0+th, y_0+tk) - f(x_0, y_0)\bigr] =
h\dfrac{\partial f}{\partial x}(x_0,y_0) + k\dfrac{\partial f}{\partial y}(x_0,y_0) + \dfrac{\lvert t \rvert }{t}
\lVert (h,k) \rVert_{ } \varepsilon(th, tk)\). Puisque \(\lvert \lvert t \rvert / t \rvert = 1\) et que \(\varepsilon(th, tk) \xrightarrow[t \rightarrow 0]{}
0\), on en déduit le résultat.
Différentielle
(Différentielle). Soit \(f : U \mapsto \mathbb{R}\) une fonction de classe \(\mathcal{C}^{1}\) et \(M_0 =
(x_0, y_0) \in U\) un point. On définit la forme linéaire : \[{\mathrm{d}f}_{M_0}: \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & \mathbb{R} \newline (h,k) & \longmapsto &
h\dfrac{\partial f}{\partial x}(x_0,y_0) + k \dfrac{\partial f}{\partial y}(x_0, y_0) \end{array} \right.\] C’est la différentielle de la fonction \(f\) au point \(M_0\).
(Gradient). On définit le gradient de \(f\) au point \(M_0\) comme étant le vecteur \(\overrightarrow{\nabla} f(M_0) = \Bigl( \dfrac{\partial f}{\partial x}(x_0,y_0),
\dfrac{\partial f}{\partial y}(x_0, y_0) \Bigr)\). Alors pour tout accroissement \(\overrightarrow{H}=(h,k)\), \[{\mathrm{D}_{\overrightarrow{H}}}{f}(M_0) = {\mathrm{d}f}_{M_0}(\overrightarrow{H}) =
\left( \overrightarrow{\nabla} f(M_0) \mid \overrightarrow{H} \right)\]
(Dérivation d’une composée). Soit \(f : U\subset \mathbb{R} [2] \mapsto \mathbb{R}\), \(u, v : I \subset \mathbb{R}
\mapsto \mathbb{R}\). On définit \(\varphi: \left\{ \begin{array}{ccl} I & \longrightarrow & \mathbb{R} [2] \newline t & \longmapsto & \bigl(u(t),v(t)\bigr) \end{array} \right.\). On suppose que :
On peut alors définir la fonction \[g = f \circ \varphi: \left\{ \begin{array}{ccl} I & \longrightarrow & \mathbb{R} \newline t & \longmapsto & f\bigl(u(t), v(t)\bigr) \end{array} \right.\] Cette fonction est de classe \(\mathcal{C}^{1}\) sur \(I\) et sa dérivée vaut : \[\boxed{g'(t) = u'(t) \dfrac{\partial f}{\partial x}\bigl(u(t), v(t)\bigr) + v'(t)
\dfrac{\partial f}{\partial y}\bigl(u(t), v(t)\bigr)}\]
\(f\) est de classe \(\mathcal{C}^{1}\) sur l’ouvert \(U\).
Les deux fonctions \(u\) et \(v\) sont de classe \(\mathcal{C}^{1}\) sur \(I\).
\(\forall t \in I\), \(\varphi(t) \in U\).
Soit \(t_0 \in I\). Nous allons montrer que \(g\) admet un développement limité à l’ordre \(1\) en \(t_0\). Puisque \(f\) est de classe \(\mathcal{C}^{1}\), elle admet un développement limité au point \(M_0=(u(t_0), v(t_0))\). Pour \(t \in I\), on peut écrire : \(f(u(t_0+h), v(t_0+h)) = f(u(t),v(t)) + \bigl[u(t_0+h)-u(t_0)\bigr]
\dfrac{\partial f}{\partial x}(u(t_0, v(t_0)) +
\bigl[v(t_0+h)-v(t_0)\bigr]\dfrac{\partial f}{\partial y}(u(t_0), v(t_0)) +
\lVert (u(t_0+h)-u(t_0), v(t_0+h)-v(t_0)) \rVert_{ }\varepsilon(u(t_0+h)-u(t_0),
v(t_0+h)-v(t_0))\). Puisque les fonctions \(u\) et \(v\) sont dérivables en \(t_0\), elles possèdent un développement limité à l’ordre \(1\) : \(u(t_0+h) = u(t_0) + hu'(t_0) + h\varepsilon_1(h)\), \(v(t_0+h)=v(t_0) +
hv'(t_0) + \varepsilon_2(h)\). En reportant dans le DL de \(f\), on trouve que \(g(t_0+h)=g(t_0) + h\bigl[u'(t_0)\dfrac{\partial f}{\partial x}(u(t_0),v(t_0)) +
v'(t_0)\dfrac{\partial f}{\partial y}(u(t_0), v(t_0))\bigr] + R(h)\) et par une majoration simple, on vérifie que \(R(h) = \petito{h}\). Nous avons donc vérifié que \(g\) était dérivable en \(t_0\) et obtenu l’expression de \(g'(t_0)\). Puisque \(\dfrac{\partial f}{\partial x}\), \(\dfrac{\partial f}{\partial y}\), \(u'\) et \(v'\) sont des fonctions continues, la fonction \(g'\) est également continue.
On peut exprimer \(g'(t_0)\) à l’aide de la différentielle et du gradient de \(f\) en \(M_0\) : \(g'(t) = {\mathrm{d}f}_{M_0}(\varphi'(t)) = \left( \overrightarrow{\nabla} f(M_0) \mid \varphi'(t) \right)\).
(Dérivées partielles d’une composée). Soit \(f : U \subset \mathbb{R} [2] \mapsto \mathbb{R}\) une fonction de classe \(\mathcal{C}^{1}\), \(x,y : V \subset \mathbb{R} [2] \mapsto \mathbb{R}\) deux fonctions de classe \(\mathcal{C}^{1}\). On suppose que \(\forall (u,v) \in V\), \(\bigl(x(u,v),
y(u,v)\bigr) \in U\). On peut alors définir la fonction \[F : \left\{ \begin{array}{ccl} U & \longrightarrow & \mathbb{R} \\ (u,v) & \longmapsto & f\bigl(x(u,v), y(u,v)\bigr) \end{array} \right.\] La fonction \(F\) est de classe \(\mathcal{C}^{1}\) et en tout point \((u,v)
\in V\), \[\boxed{
\begin{cases}
\dfrac{\partial F}{\partial u}(u,v) &= \dfrac{\partial x}{\partial u}(u,v) \dfrac{\partial f}{\partial x}(x(u,v), y(u,v)) +
\dfrac{\partial y}{\partial u}(u,v) \dfrac{\partial f}{\partial y}(x(u,v), y(u,v)) \newline
\dfrac{\partial F}{\partial v}(u,v) &= \dfrac{\partial x}{\partial v}(u,v) \dfrac{\partial f}{\partial x}(x(u,v),y(u,v)) +
\dfrac{\partial y}{\partial v}(u, v) \dfrac{\partial f}{\partial y}(x(u,v), y(u,v))
\end{cases}
}\]
Soit un point \(K = (u,v) \in V\), considérons la première fonction partielle de \(F\) en \(K\) définie par \(F_1(t) = F(t,v) = f\bigl(x(t,v), y(t,v)\bigr) = f\bigl(g_1(t),
g_2(t)\bigr)\). Les fonctions \(g_1\) et \(g_2\) sont de classe \(\mathcal{C}^{1}\) et \(g_1'(t) = \dfrac{\partial x}{\partial u}(t,v)\), \(g_2'(t) = \dfrac{\partial y}{\partial u}(t,v)\). On peut utiliser le théorème précédent : la fonction \(F_1\) est dérivable en tout point \(t\) et \(F_1'(t) = \dfrac{\partial x}{\partial u}(t,v)\dfrac{\partial f}{\partial x}(g_1(t), g_2(t)) + \dfrac{\partial y}{\partial u}(t,
v) \dfrac{\partial f}{\partial y}(g_1(t), g_2(t))\). On en déduit que \(F\) admet une première dérivée partielle au point \((u,v)\) et que \(\dfrac{\partial F}{\partial u}(u,v) = F_1'(u) = \dfrac{\partial x}{\partial u}(u,v)
\dfrac{\partial f}{\partial x}(x(u,v),y(u,v)) + \dfrac{\partial y}{\partial u}(u,v)
\dfrac{\partial f}{\partial y}(x(u,v),y(u,v))\). On fait de même pour la deuxième dérivée partielle. Ces dérivées partielles s’expriment comme composées de fonctions continues donc la fonction \(F\) est de classe \(\mathcal{C}^{1}\) sur \(V\).
Extremum d’une fonction à deux variables
(Maximum, minimum, extremum). Soient \(f:U\subset \mathbb{R}^2 \rightarrow \mathbb{R}\) et \(M_0\in U\). On dit que \(M_0\) est :
un maximum local (respectivement un maximum local strict) de \(f\) si et seulement si il existe un voisinage \(V\) de \(M_0\) dans \(\mathbb{R}^2\) tel que : \[\forall x\in V\cap U,\quad f\left(x\right)\leqslant f\left(M_0\right) \quad (\textrm{ respectivement } f\left(x\right)<f\left(M_0\right)\]
un minimum local (respectivement un minimum local strict) de \(f\) si et seulement si il existe un voisinage \(V\) de \(M_0\) dans \(\mathbb{R}^2\) tel que : \[\forall x\in V\cap U,\quad f\left(x\right)\geqslant f\left(M_0\right) \quad (\textrm{ respectivement } f\left(x\right)>f\left(M_0\right)\]
un extremum local si \(M_0\) est un maximum ou un minimum local.
un maximum global si : \[\forall x\in U,\quad f\left(x\right)\leqslant f\left(M_0\right)\]
un minimum global si : \[\forall x\in U,\quad f\left(x\right)\geqslant f\left(M_0\right)\]
un extremum global si \(M_0\) est un maximum ou un minimum global.
(La différentielle est nulle en un extremum local). Soient \(f:U\subset \mathbb{R}^2 \rightarrow \mathbb{R}\) de classe \(\mathcal{C}^{1}\) sur \(U\) et \(M_0=(x_0, y_0)\in U\). Si \(M_0\) est un extremum local de \(f\) alors \({\mathrm{d}f}_{M_0}=0\) c’est-à-dire : \(\dfrac{\partial f}{\partial x}(x_0,y_0)=\dfrac{\partial f}{\partial y}(x_0,y_0)=0\).
Supposons par exemple qu’il existe un voisinage \(V\) de \(M_0\) tel que \(M_0\) est un maximum de \(f\) sur \(V\). Considérons la première fonction partielle \(f_1\) de \(f\) au point \(M_0\) définie sur un voisinage de \(x_0\) par \(f_1(t) = f(t, y_0)\). Puisque \(x_0\) est un maximum de \(f_1\), on sait que \(f_1'(x_0) = 0\), c’est-à-dire \(\dfrac{\partial f}{\partial x}(x_0, y_0) = 0\). On fait de même avec la deuxième fonction partielle pour montrer que \(\dfrac{\partial f}{\partial y}(x_0, y_0) = 0\).
Un point où la différentielle s’annule s’appelle un point critique de la fonction.
La réciproque est en général fausse, même pour des fonctions d’une variable : la fonction définie par \(f(x) = x^3\) a une dérivée nulle en \(0\) et pourtant \(0\) n’est pas un extrémum local. Pour des fonctions de deux variables, on peut également avoir des points selles. Si \(f\) est définie sur \(\mathbb{R} [2]\) par \(f(x,y) = x^2 - y^2\), \(\dfrac{\partial f}{\partial x}(0,0) = \dfrac{\partial f}{\partial y}(0,0) = 0\) et pourtant le point \((0,0)\) n’est ni un maximum local, ni un minimum local : \(f_1(t) = f(t, 0) =
t^2\) et \(f_2(t) = f(0, t) = -t^2\).
Cherchons les extremums de la fonction définie sur \(\mathbb{R} [2]\) par \[f(x,y) = (x+y)^2 + x^4 + y^4\] Commençons par chercher les points critiques : \[\begin{cases}
\dfrac{\partial f}{\partial x}(x,y) &= 2(x+y)+4x^3 = 0 \newline
\dfrac{\partial f}{\partial y}(x,y) &= 2(x+y) + 4y^3 = 0
\end{cases}\] Le seul point critique est \((0, 0)\). Puisque \(f(x,y) \geqslant 0\) avec égalité si et seulement si \((x,y) = (0,0)\), l’origine est un minimum global de la fonction \(f\) est c’est le seul extrémum.
On considère une boîte rectangulaire sans son couvercle de volume \(V\). Déterminer les dimensions de cette boîte pour la fabriquer avec le moins de carton possible.
Notons \(x, y\) les longueurs de la base et \(h\) sa hauteur. Puisque le volume est fixé, on a \(xyh = V\). L’aire des parois en carton que l’on cherche à minimiser vaut : \[f(x,y)= 2xh + 2yh + xy = \dfrac{2V}{y} + \dfrac{2V}{x} + xy\] Cette fonction est de classe \(\mathcal{C}^{1}\) sur l’ouvert \(U = ]0,
+\infty[ \times ]0, +\infty[\) et \[\begin{cases}
\dfrac{\partial f}{\partial x}(x,y) &= y - \dfrac{2V}{x^2} \newline
\dfrac{\partial f}{\partial y}(x,y) &= x - \dfrac{2V}{y^2}
\end{cases}\] Un point critique doit vérifier \(xy = \dfrac{2V}{x} = \dfrac{2V}{y}\) d’où l’on tire \(x = y = (2V)^{1/3}\) et \(h = V^{1/3} / 2^{2/3}\). Il est clair dans notre contexte que cet unique point critique est le minimum global de la fonction.
On considère un nuage de points dans le plan : \(M_1=(x_1,y_1), \dots
,M_n = (x_n, y_n)\) que l’on suppose non alignés sur une même verticale. On recherche la droite d’équation \(y = ax + b\) qui minimise la quantité : \[f(a, b) = \displaystyle{\sum_{k=1}^{n}} \bigl[y_i - (ax_i + b) \bigr]^2\]
La fonction \(f\) est de classe \(\mathcal{C}^{1}\) sur \(\mathbb{R} [2]\) et \[\begin{cases}
\dfrac{\partial f}{\partial a}(a,b) &= -\displaystyle{\sum_{k=1}^{n}} [y_i-(ax_i+b)]x_i = a
\displaystyle{\sum_{k=1}^{n}} x_i^2 + b \displaystyle{\sum_{k=1}^{n}} x_i - \displaystyle{\sum_{k=1}^{n}} x_i
y_i \\
\dfrac{\partial f}{\partial y}(a,b) &= - \displaystyle{\sum_{k=1}^{n}} [y_i - (ax_i+b)] = a
\displaystyle{\sum_{k=1}^{n}} x_i + nb - \displaystyle{\sum_{k=1}^{n}} y_i
\end{cases}\] Pour simplifier les notations, définissons les vecteurs de \(\mathbb{R} [n]\) suivants : \(X= (x_1,\dots, x_n)\), \(Y = (y_1,\dots, y_n)\) et \(N = (1, \dots, 1)\). Les points critiques \((a,b)\) vérifient le système linéaire : \[\begin{cases}
\lVert X \rVert_{ }^2 a + \left( N \mid X \right) b &= \left( X \mid Y \right) \\
\left( N \mid X \right) a + \lVert N \rVert_{ }^2 b &= \left( N \mid Y \right)
\end{cases}\] Le déterminant du système vaut \(\mathop{\rm det}(S) = \lVert X \rVert_{ }^2 \lVert N \rVert_{ }^2 -
\left( N \mid X \right)^2 \geqslant 0\). Il est positif d’après l’inégalité de Cauchy-Schwarz et s’il était nul, d’après le cas d’égalité de Cauchy-Schwarz, les deux vecteurs \(N\) et \(X\) seraient liés et tous les points seraient sur une même verticale, ce qui est faux. Le système possède donc une solution unique et on trouve que \[\begin{cases}
a &= \dfrac{ n \left( X \mid Y \right) - \left( N \mid X \right)\left( N \mid Y \right)}{n\lVert X \rVert_{ }^2 -
\left( N \mid X \right)^2} \newline
b &= \dfrac{\lVert X \rVert_{ }^2\left( N \mid Y \right) -
\left( N \mid x \right)\left( X \mid Y \right)}{n\lVert X \rVert_{ }^2 - \left( N \mid X \right)^2}
\end{cases}\] Le seul point critique est ici le minimum global de la fonction.
(2). En pratique, on définit souvent des fonctions \(f : K \mapsto \mathbb{R}\) où \(K\) n’est pas un ouvert de \(\mathbb{R} [2]\). Pour trouver les extremums de \(f\), on procède comme suit :
Déterminer les points critiques intérieurs à \(K\), c’est-à-dire les points \(M \in K\) tels qu’il existe une boule ouverte centrée en \(M\) incluse dans \(K\) avec \(\dfrac{\partial f}{\partial x}(M) = \dfrac{\partial f}{\partial y}(M) = 0\).
Étudier la nature de ces points critiques intérieurs (maximum, minimum local, ou point selle). Cette partie est difficile à traiter avec les connaissances de math. sup. En deuxième année, vous disposerez d’un outil agréable pour déterminer la nature d’un point critique.
Étudier \(f\) sur le bord de \(K\).
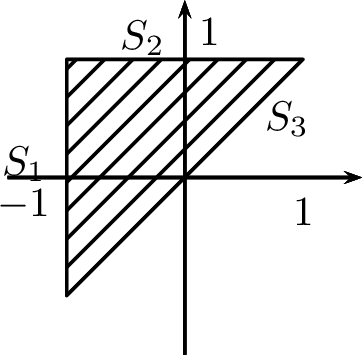
On considère le domaine \(\Delta = \{(x,y) \in \mathbb{R} [2] \mid -1 \leqslant x
\leqslant y \leqslant 1 \}\) et la fonction \(f\) définie sur \(\Delta\) par \(f(x,y) = (y-x)^3 + 6xy\). Déterminer son maximum et son minimum global.
La fonction \(f\) est de classe \(\mathcal{C}^{1}\) sur l’intérieur du domaine : \(\overset{\circ}{\Delta} = \{(x,y) \in \mathbb{R} [2] \mid -1 < x < y <
1 \}\) et on calcule \[\begin{cases}
\dfrac{\partial f}{\partial x}(x,y) &= 6y - 3(y-x)^2 \newline
\dfrac{\partial f}{\partial y}(x,y) &= 6x + 3(y-x)^2
\end{cases}\] On trouve les points critiques intérieurs \((x,y)\) qui doivent vérifier \((y-x)^2 = 2y = -2x\) d’où \(y=-x\) puis \(y=-x=1/2\). On calcule \(f(-1/2, 1/2) = -1/2\). Étudions ensuite la restriction de \(f\) sur les trois segments qui forment le bord du domaine. Sur le segment \(S_1\), \(g(t) = f(-1, t) = (1+t)^3 - 6t\). On étudie la fonction \(g\) définie sur \([-1,1]\) et on trouve que \(g\) atteint son minimum en \(t
= \sqrt{2}-1\) et ce minimum vaut \(6 - 4\sqrt{2}\) et atteint son maximum en \(t = -1\) avec \(g(-1) = 6\). On fait de même pour la restriction de \(f\) à \(S_2\) en étudiant \(h(t)
= f(t, 1)\) puis sur \(S_3\) avec \(k(t) = f(t,t)\) pour \(t \in [-1, 1]\). On trouve finalement que \(f\) admet son minimum global au point critique intérieur et que ce minimum vaut \(-1/2\) et que \(f\) admet son maximum global sur la frontière qui vaut \(6\).
Le domaine \(\Delta\) est un triangle :
Dérivées partielles d’ordre \(2\)
(Dérivées partielles d’ordre \(2\)). Soit \(U \subset \mathbb{R}^2\) un ouvert et \(f : U \mapsto \mathbb{R}\) une fonction numérique de classe \({\mathcal{C}}^[(1) ]{U, \mathbb{R} }\). On peut donc définir les fonctions dérivées partielles : \[\dfrac{\partial f}{\partial x} : \left\{ \begin{array}{ccl} U & \longrightarrow & \mathbb{R} \\ a & \longmapsto & \dfrac{\partial f}{\partial x}(a) \end{array} \right.
\quad \textrm{ et} \quad\dfrac{\partial f}{\partial y} : \left\{ \begin{array}{ccl} U & \longrightarrow & \mathbb{R} \\ a & \longmapsto & \dfrac{\partial f}{\partial y}(a) \end{array} \right.\] On dit que \(f\) est de classe \({\mathcal{C}}^[(2) ]{U, \mathbb{R} }\) lorsque les \(2\) fonctions \(\dfrac{\partial f}{\partial x}\) et \(\dfrac{\partial f}{\partial y}\) sont de classe \({\mathcal{C}}^[(1) ]{U,
\mathbb{R} }\). On note alors \[\dfrac{\partial ^2 f}{\partial x^2}(a) = \dfrac{\partial \dfrac{\partial f}{\partial x}}{\partial x}(a),\quad
\dfrac{\partial^{2}f}{\partial x \partial y}(a) = \dfrac{\partial \dfrac{\partial f}{\partial y}}{\partial x}(a),\] \[\dfrac{\partial ^2 f}{\partial y^2}(a) = \dfrac{\partial \dfrac{\partial f}{\partial y}}{\partial y}(a),\quad
\dfrac{\partial^{2}f}{\partial y \partial x}(a) = \dfrac{\partial \dfrac{\partial f}{\partial x}}{\partial y}(a).\]
Hermann Schwarz né le 25 Janvier 1843 à Hermsdorf (Silésie) et mort le 30 Novembre 1921 à Berlin Hermann Schwarz a commencé ses études à l’université de Berlin pour apprendre la chimie mais les cours de Kümmer et de Weierstrass lui font abandonner son idée première et il décide de se consacrer aux mathématiques. Il effectue sa thèse sous la direction de Weierstrass. Il est nommé maître de conférence à Halle en 1867, puis professeur à Zurich en 1869 et rejoint l’université de Göttingen en 1875 pour finalement prendre un poste à Berlin en 1892. Schwarz est au départ très intéressé par la géométrie et, au contact de Weierstrass, il apprend à traduire ses idées avec les outils de l’analyse. En 1870, il résout le problème de Dirichlet qui consiste à trouver une fonction harmonique définie sur un ouvert prolongeant une fonction continue définie sur la frontière de l’ouvert. La plus importante de ses contributions a été celle aux surfaces minimales (les surfaces minimisant leur aire relativement à une contrainte donnée). C’est dans un travail relatif à ce sujet qu’il publie, pour des intégrales doubles, l’inégalité page qui porte maintenant son nom. Elle est en fait due à Bunyakowsky qui l’énonça le premier pour des intégrales simples. Notons que Cauchy, dans son cours à Polytechnique, l’avait aussi énoncé dans le cas des suites.
(Théorème de Schwarz). Soit \(f : U \mapsto \mathbb{R}\) une fonction de classe \({\mathcal{C}}^[(2) ]{U, \mathbb{R} }\). Alors en tout point \(a \in U\), \[\boxed{\dfrac{\partial^{2}f}{\partial x \partial y}(a) = \dfrac{\partial^{2}f}{\partial y \partial x}(a)}\]
Voir l’exercice [exo_preuve_theo_schwarz] page [exo_preuve_theo_schwarz].
Considérons la fonction \[f : \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & \mathbb{R} \\ (x,y) & \longmapsto &
\begin{cases}
\dfrac{xy(x^2-y^2)}{x^2+y^2} & \textrm{ si } (x, y) \neq (0, 0) \\
0 & \textrm{ si } (x, y) = (0, 0)
\end{cases}
\end{array} \right.\] On vérifie facilement que la fonction \(f\) est de classe \(\mathcal{C}^{1}\) sur \(\mathbb{R} [2]\) et que \[\dfrac{\partial f}{\partial x}(x,y) = \begin{cases}
\dfrac{3x^2y - y^3}{(x^2 + y^2)} - \dfrac{2x(yx^3 -
xy^3)}{(x^2+y^2)^2} & \textrm{ si } (x,y) \neq (0,0) \\
0 & \textrm{ si } (x,y) = (0, 0)
\end{cases} \quad
\dfrac{\partial f}{\partial y}(x,y) = \begin{cases}
\dfrac{x^3 - 3xy^2}{x^2 + y^2} - \dfrac{2y(yx^3 - x y^3)}{(x^2 +
y^2)^2} & \textrm{ si }(x,y) \neq (0,0) \newline
0 & \textrm{ si } (x,y)=(0,0)
\end{cases}\] Formons le taux d’accroissement : \[\dfrac{1}{t}\bigl[\dfrac{\partial f}{\partial x}(0,t) - \dfrac{\partial f}{\partial x}(0,0)\bigr]= -1
\xrightarrow[t \rightarrow 0]{} -1\] ce qui montre que \(\dfrac{\partial \dfrac{\partial f}{\partial x}}{\partial y}(0,0) = -1\). De même, formons le taux d’accroissement \[\dfrac{1}{t}\bigl[\dfrac{\partial f}{\partial y}(t,0) - \dfrac{\partial f}{\partial y}(0,0)\bigr]= 1
\xrightarrow[t \rightarrow 0]{} 1\] ce qui montre que \(\dfrac{\partial \dfrac{\partial f}{\partial y}}{\partial x}(0,0) = 1\). Les deux dérivées partielles secondes croisées sont différentes. On peut vérifier l’existence des quatre fonctions dérivées partielles secondes sur \(\mathbb{R} [2]\), mais on vérifie qu’elles ne sont pas continues en \((0,0)\).
(Formule de Taylor intégrale à l’ordre \(2\)). Soit \(f : U \mapsto \mathbb{R}\) une fonction de classe \(\mathcal{C}^{2}\). On suppose que \(U\) est un ouvert convexe. Soit \(M_0=(x_0, y_0) \in U\) et un accroissement \(\overrightarrow{H}=(h,k)\) tel que \(M_0 + \overrightarrow{H}
\in U\). On a : \[f(x_0+h, y_0+k) = f(x_0, y_0) + \Bigl[
\underbrace{h\dfrac{\partial f}{\partial x}(x_0, y_0) + k\dfrac{\partial f}{\partial y}(x_0,
y_0)}_{{\mathrm{d}f}_{M_0}(\overrightarrow{H})} \Bigr] + R(h,k)\] où \[R(h, k) = \displaystyle{\int_{0}^{1}} (1-t)\bigl[ h^2 \dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0+th,y_0+tk) +
2hk\dfrac{\partial^{2}f}{\partial x \partial y}(x_0+th,y_0+tk) + k^2\dfrac{\partial^{2} f}{\partial {y}^{2}}(x_0+th, y_0+tk)
\bigr] \mathrm{ \;d}t\]
(2). La preuve est instructive. On se ramène aux théorèmes déjà prouvés pour les fonctions d’une variable en considérant la fonction \[\varphi: \left\{ \begin{array}{ccl} [0,1] & \longrightarrow & \mathbb{R} \newline t & \longmapsto & f(x_0+th, y_0+tk) \end{array} \right.\] Cette fonction est définie sur \([0, 1]\) car on a supposé que l’ouvert \(U\) était convexe. Elle est de classe \(\mathcal{C}^{1}\) d’après le théorème de dérivée d’une composée () et \(\forall t \in [0, 1]\), \[\varphi'(t) = h \dfrac{\partial f}{\partial x}(x_0+th, y_0+tk) + k
\dfrac{\partial f}{\partial y}(x_0+th,y_0+tk)\] En ré-appliquant le même théorème, on vérifie que \(\varphi\) est de classe \(\mathcal{C}^{2}\) sur \([0, 1]\) avec \(\varphi''(t) = h^2 \dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0+th,y_0+tk) +
hk\dfrac{\partial^{2}f}{\partial x \partial y}(x_0+th,y_0+tk) + kh\dfrac{\partial^{2}f}{\partial y \partial x}(x_0+th,y_0+tk) +
k^2 \dfrac{\partial^{2} f}{\partial {y}^{2}}(x_0+th,y_0+tk)\). Avec le théorème de Schwarz, \(\varphi''(t) = h^2 \dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0+th,y_0+tk) +
2hk\dfrac{\partial^{2}f}{\partial x \partial y}(x_0+th,y_0+tk)+
k^2 \dfrac{\partial^{2} f}{\partial {y}^{2}}(x_0+th,y_0+tk)\). Il suffit alors d’écrire la formule de Taylor intégrale à l’ordre \(1\) pour la fonction \(\varphi\) entre \(0\) et \(1\) : \[\varphi(1) = \varphi(0) + \varphi'(0) + \displaystyle{\int_{0}^{1}} (1-t)\varphi''(t)
\mathrm{ \;d}t\] pour obtenir le résultat.
(Formule de Taylor-Young à l’ordre \(2\)). Si \(f : U \mapsto \mathbb{R}\) est de classe \(\mathcal{C}^{2}\) sur l’ouvert convexe \(U \subset \mathbb{R} [2]\), pour \((x_0, y_0) \in U\) et \((h, k) \in
\mathbb{R} [2]\) tel que \((x_0+h,y_0+k) \in U\), \[f(x_0+h, y_0+k) = f(x_0,y_0) + h\dfrac{\partial f}{\partial x}(x_0,y_0) + k
\dfrac{\partial f}{\partial y}(x_0, y_0) + \dfrac{1}{2}\bigl[h^2 \dfrac{\partial^{2} f}{\partial {(}^{2}}x_0,y_0) +
2hk\dfrac{\partial^{2}f}{\partial x \partial y}(x_0, y_0) + \dfrac{\partial^{2} f}{\partial {y}^{2}}(x_0,y_0)\bigr]
+ \lVert (h,k) \rVert_{ }^2R(h, k)\] avec \(R(h,k) \xrightarrow[(h,k) \rightarrow (0,0)]{} 0\).
Reprenons la formule de Taylor-intégrale et travaillons sur le reste. Écrivons \(\displaystyle{\int_{0}^{1}} (1-t) \dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0+th,y_0+tk)\mathrm{ \;d}t =
\dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0, y_0) \displaystyle{\int_{0}^{1}} (1-t)\mathrm{ \;d}t + \varepsilon_1(h,k)\) où \(\varepsilon_1(h, k) = \displaystyle{\int_{0}^{1}} (1-t)\bigl[\dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0+th,y_0+tk) -
\dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0, y_0)\bigr] \mathrm{ \;d}t\). Puisque \(\displaystyle{\int_{0}^{1}} (1-t) \mathrm{ \;d}t = 1/2\), on fait apparaître dans \(R(h,k)\), \({\scriptstyle 1\over\scriptstyle 2} h^2 \dfrac{\partial^{2} f}{\partial {x}^{2}}(x_0, y_0)\). Puisque la fonction \(\dfrac{\partial^{2} f}{\partial {x}^{2}}\) est continue en \((x_0, y_0)\), on montre avec \(\varepsilon\) que \(\varepsilon_1(h, k) \xrightarrow[(h,k) \rightarrow (0,0)]{} 0\). On fait de même avec les deux autres termes du reste pour obtenir le résultat.
La partie entre crochet est une forme quadratique \(q(h,k)\) en l’accroissement \((h, k)\). Le reste peut s’écrire \(\petito{\lVert (h,k) \rVert_{ }^2}\). La formule de Taylor-Young permettra d’étudier la nature d’un point critique en math. spé.
Exemples d’équations aux dérivées partielles
Le but de ce paragraphe est de résoudre quelques équations aux dérivées partielles simples. Pour simplifier l’étude, on considère un ouvert de la forme \(U = ]a, b[ \times ]c, d[\). Commençons par résoudre des équations aux dérivées partielles fondamentales :
(EDP \(\dfrac{\partial f}{\partial x} = 0\)). \[\boxed{(E_1)~: \dfrac{\partial f}{\partial x}(x,y) = 0}\] Une fonction \(f \in {\mathcal{C}}^[(1) ]{U, \mathbb{R} }\) est solution de \((E_1)\) si et seulement s’il existe une fonction d’une variable \(k \in {\mathcal{C}}^[(1) ]{]c,d[,\mathbb{R} }\) telle que \(\forall (x,y) \in U, \boxed{f(x,y) = k(y)}\).
Supposons que \(f \in {\mathcal{C}}^[(1) ]{U, \mathbb{R} }\) est solution de \((E_1)\). Fixons \(y\in\left]c,d\right[\). La fonction : \(\varphi: \left\{ \begin{array}{ccl} \left]a,b\right[ & \longrightarrow & \mathbb{R} \\ t & \longmapsto & f\left(t,y\right) \end{array} \right.\) est dérivable sur \(\mathbb{R}\) et de dérivée nulle. Elle est donc constante : \(\forall t\in\left]a,b\right[\), \(\varphi\left(t\right)=\varphi\left(0\right)\) et on a donc : \(\forall \left(x,y\right)\in U,\quad f\left(x,y\right)=k\left(y\right)\) avec \(k: \left\{ \begin{array}{ccl} \left]c,d\right[ & \longrightarrow & \mathbb{R} \newline y & \longmapsto & f\left(0,y\right) \end{array} \right.\) qui est une fonction de classe \(\mathcal{C}^{1}\) sur \(]c,d[\) d’après le théorème de composée .
Réciproquement, une fonction \(k \in {\mathcal{C}}^[(1) ]{]c,d[,\mathbb{R} }\) est clairement solution de \((E_1)\).
(EDP \(\dfrac{\partial f}{\partial x} = h\)). Soit \(h \in {\mathcal{C}}^[(0) ]{]a,b[,\mathbb{R} }\). \[\boxed{(E_2)~: \dfrac{\partial f}{\partial x}(x,y) = h(x)}\] Une fonction \(f\in {\mathcal{C}}^[(1) ]{U, \mathbb{R} }\) est solution de \((E_2)\) si et seulement s’il existe une fonction d’une variable \(k \in {\mathcal{C}}^[(1) ]{]c,d[,\mathbb{R} }\) telle que \(\forall (x,y) \in U\), \(\boxed{f(x,y) = H(x) + k(y)}\) où \(H\) est une primitive de \(h\) sur \(]a, b[\).
D’après le théorème fondamental de l’analyse, comme \(h\) est continue sur \(\left]a,b\right[\), elle possède une primitive \(H\) sur \(\left]a,b\right[\). Soit \(f\in {\mathcal{C}}^[(1) ]{U, \mathbb{R} }\). Introduisons la fonction \(\psi: \left\{ \begin{array}{ccl} U & \longrightarrow & \mathbb{R} \\ \left(x,y\right) & \longmapsto & f\left(x,y\right)-H\left(x\right) \end{array} \right.\). Supposons que \(f\) est solution de \((E_2)\), alors : \[\begin{aligned}
& & \forall (x,y) \in U, \quad \dfrac{\partial f}{\partial x}(x,y) = h(x)\\
&\Rightarrow & \forall (x,y) \in U, \quad \dfrac{\partial \left(f-H\right)}{\partial x}(x,y) = 0\\
&\Rightarrow & \psi \textrm{ est solution de } \left(E_0\right)\\
&\Rightarrow & \forall \left(x,y\right)\in U,\quad \psi\left(x,y\right)=k\left(y\right)
\textrm{ avec } k: \left\{ \begin{array}{ccl} \left]c,d\right[ & \longrightarrow & \mathbb{R} \\ y & \longmapsto & f\left(0,y\right) \end{array} \right. \newline
&\Rightarrow & \forall (x,y) \in U, \quad f(x,y) = H(x) + k(y)
\end{aligned}\] Réciproquement, on vérifie qu’une fonction de cette forme est solution de \(\left(E_2\right)\).
( EDP \(\dfrac{\partial^{2}f}{\partial x \partial y} = 0\)). \[\boxed{(E_3)~: \dfrac{\partial^{2}f}{\partial x \partial y} = 0}\] Une fonction \(f \in {\mathcal{C}}^[(2) ]{U, \mathbb{R} }\) est solution de \((E_3)\) si et seulement s’il existe deux fonctions \(H \in {\mathcal{C}}^[(2) ]{]a,b[,\mathbb{R} }\) et \(K \in {\mathcal{C}}^[(2) ]{]c,d[,\mathbb{R} }\) telles que : \[\forall (x,y) \in U,\quad \boxed{f(x,y) = H(x) + K(y)}\]
Soit \(f \in {\mathcal{C}}^[(2) ]{U,\mathbb{R} }\). Supposons que \(f\) est solution de \((E_3)\). Alors : \[\begin{aligned}
& & \dfrac{\partial f}{\partial y} \textrm{ est solution de } \left(E_1\right)\\
&\Rightarrow & \exists k \in {\mathcal{C}}^[(1) ]{]c,d[,\mathbb{R} }: \quad \forall (x,y) \in
U,\quad
\dfrac{\partial f}{\partial y}(x,y) = k(y)\\
&\Rightarrow & f \textrm{ est solution de } (E_2)\newline
&\Rightarrow & \forall (x,y) \in U,\quad f(x,y) = H(x) + K(y) \end{aligned}\]
Réciproquement, on vérifie qu’une fonction de cette forme est solution de \(\left(E_3\right)\).
où \(K\) est une primitive de \(k\) et est donc de classe \(\mathcal{C}^{2}\) et où \(K \in {\mathcal{C}}^[(1) ]{]c,d[,\mathbb{R} }\). Comme : \(\forall (x,y) \in U,\quad K(y)=H(x)-f(x,y)\), \(K\) est de classe \(\mathcal{C}^{2}\) comme différence de fonctions de classe \(\mathcal{C}^{2}\).
(EDP \(\dfrac{\partial^{2} f}{\partial {y}^{2}} = 0\)). \[\boxed{(E_4)~: \dfrac{\partial^{2} f}{\partial {y}^{2}} = 0}\] Une fonction \(f \in {\mathcal{C}}^[(2) ]{U,\mathbb{R} }\) est solution de \((E_4)\) si et seulement s’il existe une fonction \(\varphi\in {\mathcal{C}}^[(2) ]{]a,b[,\mathbb{R} }\) et \(\psi \in {\mathcal{C}}^[(2) ]{]a,b[,\mathbb{R} }\) telles que \[\forall (x,y) \in U,\quad
\boxed{f(x,y) = y\varphi(x) + \psi(x)}\]
Soit \(f \in {\mathcal{C}}^[(2) ]{U,\mathbb{R} }\). Supposons que \(f\) est solution de \((E_4)\) alors : \[\begin{aligned}
& & \dfrac{\partial f}{\partial y} \textrm{ est solution de } \left(E_1\right)\\
&\Rightarrow & \exists \varphi\in {\mathcal{C}}^[(1) ]{]a,b[,\mathbb{R} }: \quad
\forall (x,y) \in U,\quad \dfrac{\partial f}{\partial y}(x,y) = \varphi(x)\\
&\Rightarrow & \forall (x,y) \in U,\quad \dfrac{\partial \left(f-y\varphi\right)}{\partial y}(x,y) =0\\
&\Rightarrow & f-y\varphi\textrm{ est solution de } (E_1)\newline
&\Rightarrow & \exists \psi \in {\mathcal{C}}^[(1) ]{]a,b[,\mathbb{R} }: \quad \forall (x,y) \in
U,\quad f\left(x,y\right)-y\varphi\left(x\right) = \psi(x)\end{aligned}\] Réciproquement, on vérifie qu’une fonction de cette forme est solution de \(\left(E_4\right)\).
(Difféomorphisme). Soit \(U \subset E\) et \(V \subset F\). On dit qu’une application \(\varphi: U \mapsto V\) est un \(\mathcal{C}^{1}\)-difféomorphisme lorsque :
\(\varphi\) est une bijection de \(U\) vers \(V\) ;
\(\varphi\) est de classe \(\mathcal{C}^{1}\) sur \(U\) ;
\(\varphi^{-1}: V \mapsto U\) est de classe \(\mathcal{C}^{1}\) sur \(V\).
Considérons une application linéaire : \[\varphi: \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & \mathbb{R} [2] \newline (x,y) & \longmapsto & (ax+by, cx+dy) \end{array} \right.\] Elle est de classe \(\mathcal{C}^{1}\) et est bijective si et seulement si \(\mathop{\rm det}(\varphi) = ad-bc \neq
0\). La bijection réciproque est encore une application de classe \(\mathcal{C}^{1}\) et donc \(\varphi\) définit un \(\mathcal{C}^{1}\)-difféomorphisme.
Considérons l’ouvert \(U = ]0, +\infty[ \times \mathbb{R} = \{(x,y) \in
\mathbb{R} [2] \mid x > 0 \}\). Tout point \(M=(x,y) \in U\) peut être décrit à l’aide de coordonnées polaires \(x = r \cos \theta\), \(y = r\sin
\theta\) avec \((r, \theta) \in V = ]0, +\infty[ \times ]-\pi/2,
\pi/2[\). Vérifions que l’application \[\varphi: \left\{ \begin{array}{ccl} V & \longrightarrow & U \\ (r,\theta) & \longmapsto & (r\cos\theta, r\sin\theta) \end{array} \right.\] est un \(\mathcal{C}^{1}\)-difféomorphisme de \(V\) vers \(U\). L’application \(\varphi\) est bien de classe \(\mathcal{C}^{1}\) et on calcule facilement sa bijection réciproque : \[\varphi^{-1} : \left\{ \begin{array}{ccl} U & \longrightarrow & V \newline (x,y) & \longmapsto & (\sqrt{x^2+y^2}, \operatorname{arctan} (y /
x)) \end{array} \right.\] qui est également de classe \(\mathcal{C}^{1}\).
(Pour résoudre une équation aux dérivées partielles).
On utilise un changement de variables pour se ramener à une EDP plus simple. Soit \(\varphi: U_1 \mapsto U_2\) un \(\mathcal{C}^{k}\)-difféomorphisme.
On pose \(g = f \circ \varphi^{-1}\), \(f = g \circ \varphi\). \(f\) est une fonction \({\mathcal{C}}^[(k) ]{U_1,\mathbb{R} }\) solution d’une EDP \((E_1)\) si et seulement si \(g\) est une fonction \({\mathcal{C}}^[(k) ]{U_2,\mathbb{R} }\) solution d’une EDP \((E_2)\).
On considère l’ouvert \(U = ]0, +\infty[ \times \mathbb{R}\). Résoudre sur \(U\) les équations aux dérivées partielles
\((E_1)~: y\dfrac{\partial f}{\partial x}(x,y) - x \dfrac{\partial f}{\partial y}(x,y) = 0\).
\((E_2)~: x\dfrac{\partial f}{\partial x}(x,y) + y\dfrac{\partial f}{\partial y}(x,y) = 0\).
\((E)~: x\dfrac{\partial f}{\partial x}(x,y) + y\dfrac{\partial f}{\partial y}(x,y) = f(x,y) - (x^2+y^2)\).
Considérons le changement de variables polaires, c’est-à-dire le \(\mathcal{C}^{1}\)-difféomorphisme \(\varphi\) de la remarque précédente. Pour \(f : U \mapsto \mathbb{R}\) de classe \(\mathcal{C}^{1}\), on pose \(g = f \circ \varphi\) : \[g : \left\{ \begin{array}{ccl} V & \longrightarrow & \mathbb{R} \\ (\rho, \theta) & \longmapsto & f(\rho\cos\theta, \rho\sin\theta) \end{array} \right.\] et on calcule : \[\begin{cases} \dfrac{\partial g}{\partial \rho}(\rho, \theta) &= \cos\theta\dfrac{\partial f}{\partial x}(\rho\cos\theta, \rho\sin\theta) + \sin\theta\dfrac{\partial f}{\partial y}(\rho\cos\theta, \rho\sin\theta) \newline \dfrac{\partial g}{\partial \theta}(\rho,\theta) &= -\rho\sin\theta\dfrac{\partial f}{\partial x}(\rho\cos\theta, \rho\sin\theta) + \rho\cos\theta \dfrac{\partial f}{\partial y}(\rho\cos\theta, \rho\sin\theta) \end{cases}\]
Si \(f\) est solution de \((E_1)\), on doit avoir \(\forall (\rho,\theta) \in V\), \(\dfrac{\partial g}{\partial \theta}(\rho,\theta) = 0\) et donc il existe une fonction \(h : ]0, +\infty[ \mapsto \mathbb{R}\) de classe \(\mathcal{C}^{1}\) telle que \(g(\rho, \theta) = h(r)\). Par conséquent, \(f(x,y) = h(\sqrt{x^2 + y^2})\). Définissons une nouvelle fonction \(H : ]0, +\infty[\mapsto \mathbb{R}\) par \(H(u) = h(\sqrt{u})\) (elle est encore \(\mathcal{C}^{1}\)), \(f(x,y) = H(x^2 + y^2)\). On vérifie réciproquement que pour toute fonction \(H \in {\mathcal{C}}^[(1) ]{]0,+\infty[,\mathbb{R} }\), \(f\) ainsi définie est solution de \((E_1)\).
Si \(f\) est solution de \((E_2)\), la fonction \(g\) doit vérifier \(\dfrac{\partial g}{\partial \rho}=0\) et donc il existe une fonction \(h \in {\mathcal{C}}^[(1) ]{]-\pi/2, \pi/2[}\) telle que \(\forall (\rho, \theta) \in V\), \(g(\rho, \theta) = h(\theta)\). On en déduit alors que \(\forall (x,y) \in U\), \(f(x,y) = g(\operatorname{arctan} (y/x))\) et en définissant une nouvelle fonction par \(G(u) = g(\operatorname{arctan} u)\), \(f(x,y) = G(y/x)\). Réciproquement, pour toute fonction \(G \in {\mathcal{C}}^[(1) ]{]-\pi /2, \pi/2[}\), \(f\) ainsi définie est solution de \((E_2)\).
Si \(f\) est solution de \((E_3)\), \[\rho\dfrac{\partial g}{\partial \rho}(\rho,\theta) - g(\rho,\theta) = -\rho^2\] En posant \(h(\rho,\theta) = e^{-\ln \rho}g(\rho,\theta) =\dfrac{1}{\rho} g(\rho, \theta)\), \(\dfrac{\partial h}{\partial \rho}(\rho,\theta) = -1\) d’où \(g(\rho, \theta)= -\rho^2 + \rho k(\theta)\) avec \(k \in {\mathcal{C}}^[(1) ]{]-\pi,\pi[,\mathbb{R} }\). Finalement, \[f(x,y) = -(x^2+y^2) + \sqrt{x^2+y^2}k\Bigl(2\operatorname{arctan} \dfrac{y}{x+\sqrt{ x^2+y^2}}\Bigr)\]
Résoudre sur \(U = \mathbb{R} [2]\) l’équation des ondes : \[(E)~: \dfrac{\partial^{2} f}{\partial {x}^{2}} - \dfrac{\partial^{2} f}{\partial {t}^{2}} = 0\] On pose \(\varphi:\left(x,t\right)\rightarrow \left(u,v\right)=
\left(\varphi_1\left(x,t\right),\varphi_2\left(x,t\right)\right)=\left(x-t,x+t\right)\). Si \(f=g\circ \varphi\), on a : \[\begin{aligned}
\left(\begin{array}{cc}
\dfrac{\partial f}{\partial x}\left(x,t\right) &
\dfrac{\partial f}{\partial t}\left(x,t\right)
\end{array}\right)
&=&
\left(\begin{array}{cc}
\dfrac{\partial g}{\partial u}\left(\varphi\left(x,t\right)\right) &
\dfrac{\partial g}{\partial v}\left(\varphi\left(x,t\right)\right)
\end{array}\right)
\left(\begin{array}{cc}
\dfrac{\partial \varphi_1}{\partial x}\left(x,t\right)& \dfrac{\partial \varphi_1}{\partial t}\left(x,t\right)\\[0.4cm]
\dfrac{\partial \varphi_2}{\partial x}\left(x,t\right)&\dfrac{\partial \varphi_2}{\partial t}\left(x,t\right)
\end{array}\right)\\
&=&
\left(\begin{array}{cc}
\dfrac{\partial g}{\partial u}\left(\varphi\left(x,t\right)\right) &
\dfrac{\partial g}{\partial v}\left(\varphi\left(x,t\right)\right)
\end{array}\right)
\left(\begin{array}{cc}
1& -1\\[0.4cm]
1&1
\end{array}\right)
\end{aligned}\] On a donc : \[\dfrac{\partial f}{\partial x}=\dfrac{\partial g}{\partial u}+\dfrac{\partial g}{\partial v} \quad \textrm{ et} \quad\dfrac{\partial f}{\partial t}=-\dfrac{\partial g}{\partial u}+\dfrac{\partial g}{\partial v}\] Par suite : \[\begin{aligned}
\dfrac{\partial ^2f}{\partial x^2}&=&\dfrac{\partial }{\partial x}\left(\dfrac{\partial g}{\partial u}+\dfrac{\partial g}{\partial v}\right)\\
&=&\dfrac{\partial ^2 g}{\partial u^2} \dfrac{\partial \varphi_1}{\partial x} + \dfrac{\partial^{2}
g}{\partial v \partial u}\dfrac{\partial \varphi_2}{\partial x} +
\dfrac{\partial^{2}g}{\partial u \partial v}\dfrac{\partial \varphi_1}{\partial x} + \dfrac{\partial ^2 g}{\partial v^2} \dfrac{\partial \varphi_2}{\partial x}\\
&=&\dfrac{\partial ^2 g}{\partial u^2} + 2\dfrac{\partial^{2} g}{\partial u \partial v} + \dfrac{\partial ^2 g}{\partial v^2}
\end{aligned}\] \[\begin{aligned}
\dfrac{\partial ^2f}{\partial t^2}&=&\dfrac{\partial }{\partial t}\left(-\dfrac{\partial g}{\partial u}+\dfrac{\partial g}{\partial v}\right)\\
&=&-\dfrac{\partial ^2 g}{\partial u^2} \dfrac{\partial \varphi_1}{\partial t} - \dfrac{\partial^{2}
g}{\partial v \partial u}\dfrac{\partial \varphi_2}{\partial t}
+ \dfrac{\partial^{2}g}{\partial u \partial v}\dfrac{\partial \varphi_1}{\partial t} + \dfrac{\partial ^2 g}{\partial v^2} \dfrac{\partial \varphi_2}{\partial t}\newline
&=&-\dfrac{\partial ^2 g}{\partial u^2} - 2\dfrac{\partial^{2} g}{\partial u \partial v} + \dfrac{\partial ^2 g}{\partial v^2}
\end{aligned}\]
et \((E) \Leftrightarrow \left(\widetilde E\right)~:\dfrac{\partial^{2} g}{\partial u \partial v} =0\) qui est du type \(\left(E_3\right)\). Les solutions de \(\left(\widetilde E\right)\) sont donc de la forme : \(g:\left(u,v\right)\mapsto H\left(u\right)+K\left(v\right)\) où \(H \in {\mathcal{C}}^[(2) ]{\mathbb{R},\mathbb{R} }\) et \(K \in {\mathcal{C}}^[(2) ]{\mathbb{R},\mathbb{R} }\). et les solutions de \(\left(E\right)\) sont alors de la forme : \(f:\left(x,t\right) \mapsto H\left({\scriptstyle x+y\over\scriptstyle 2}\right) +
K\left({\scriptstyle x-y\over\scriptstyle 2}\right)\).
Résoudre sur \(U = ]0, +\infty[^2\) l’équation \[(E)~: x^2 \dfrac{\partial^{2} f}{\partial {x}^{2}} - y^2 \dfrac{\partial^{2} f}{\partial {y}^{2}} + x\dfrac{\partial f}{\partial x} -
y \dfrac{\partial f}{\partial y} = 0\] On pose \[\varphi: \left\{ \begin{array}{ccl} \mathbb{R} [2] & \longrightarrow & U \\ (u, v) & \longmapsto & (e^u, e^v) \end{array} \right.\] On vérifie facilement que \(\varphi\) est un \(\mathcal{C}^{2}\)-difféomorphisme et on posant \(g = f\circ \varphi\), on a \(f(x,y) = g(\ln x, \ln y)\). Après calculs, la fonction \(g\) vérifie l’équation des ondes donc il existe deux fonctions d’une variable de classe \(\mathcal{C}^{2}\) \(H\) et \(K\) telles que \(g(u,v) = H(u+v) + K(u-v)\) d’où l’existence de deux fonctions de classe \(\mathcal{C}^{2}\) d’une variable telles que \[f(x,y) = \varphi(xy) + \psi(x/y)\] On vérifie réciproquement que toute fonction de cette forme est solution de l’EDP.
Bibliographie
Barre utilisateur
[ID: 71] [Date de publication: 28 décembre 2021 13:44] [Catégorie(s): Le cours de SUP ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]Commentaires sur le cours
Documents à télécharger
L'article complet