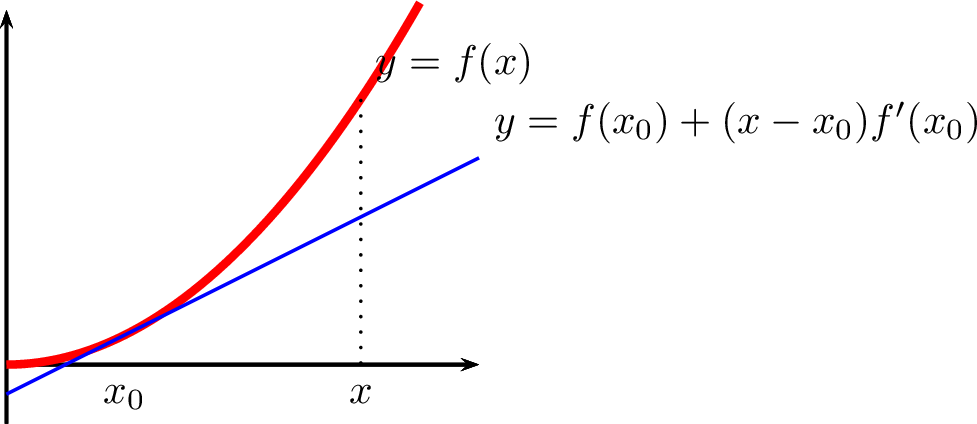Lecture zen
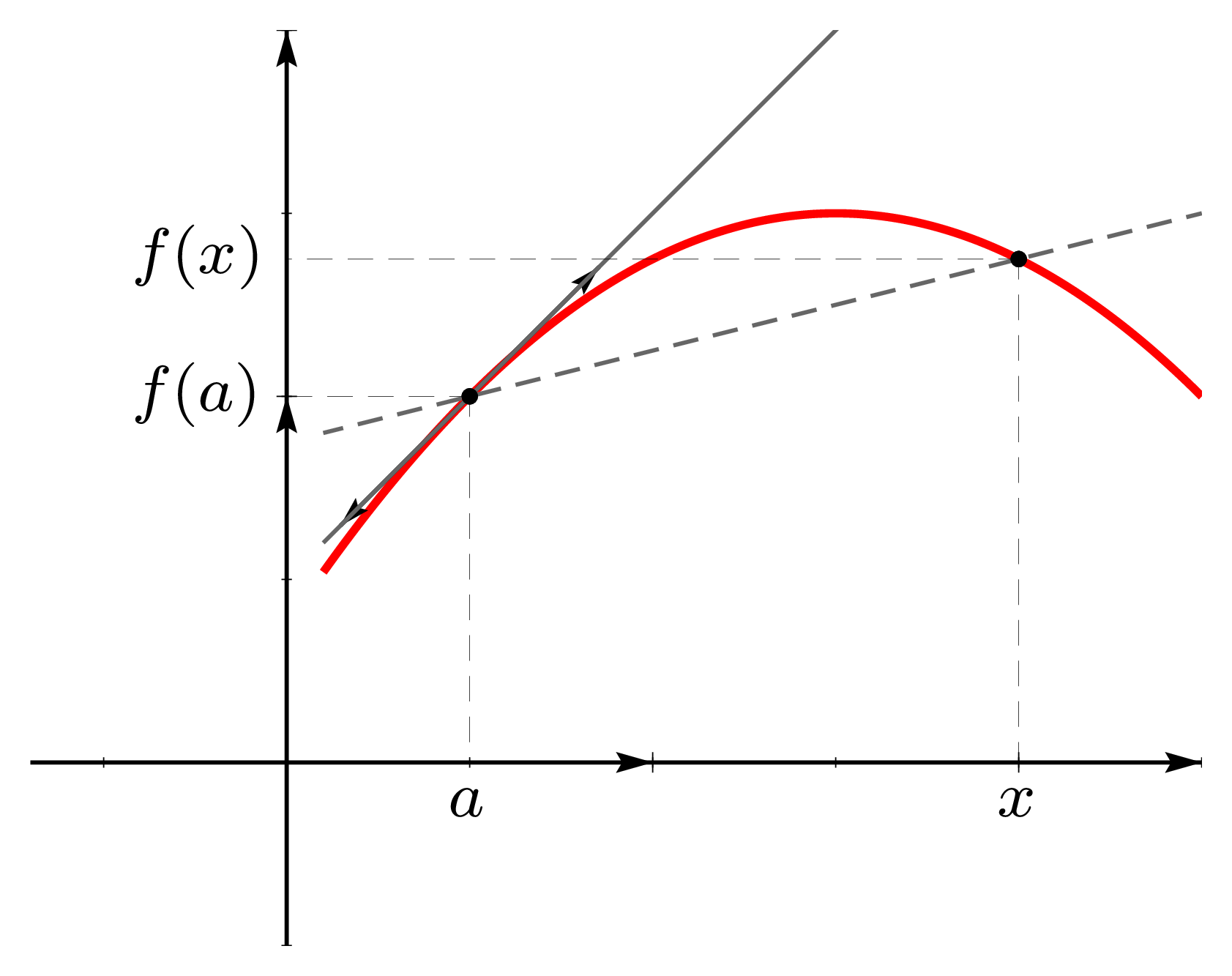
Soient \(f\in \mathscr F \left(I,\mathbb{R}\right)\) et \(a\in I\). Le plan étant ramené à un repère orthonormé, pour \(x \in I\setminus \left\{ a \right\}\), considérons la droite joignant les points \(A \left|\begin{matrix} a \\ f(a) \end{matrix} \right.\) et \(M \left|\begin{matrix} x \\ f(x) \end{matrix} \right.\). La pente de la droite \((AM)\) est donnée par \[\Delta_a(x)={\dfrac{f(x)-f(a)}{x-a}}\] Si la fonction \(f\) est dérivable au point \(a\in I\), cette pente a pour limite \(f'(a)\) quand \(x\) tend vers \(a\). Le vecteur de composante \(\left|\begin{matrix} 1 \\ \Delta_a(x) \end{matrix} \right.\) dirige la corde \((AM)\) et tend vers \(\left|\begin{matrix} 1 \newline f'(a) \end{matrix} \right.\). La droite passant par \(A\) et de pente \(f'(a)\) est donc tangente à la courbe d’équation \(y=f(x)\). C’est la position limite des cordes \((AM)\) quand \(M\) tend vers \(A\).
Dérivabilité en un point, sur un intervalle puis les fameux théorèmes de Rolle et des accroissements finis.
Dérivation des fonctions réelles à variable réelle
Dérivabilité en un point, sur un intervalle puis les fameux théorèmes de Rolle et des accroissements finis.
On dit qu’une grandeur est la limite d’une autre grandeur, quand la seconde peut s’approcher de la première plus près que d’une grandeur donnée, si petite qu’on puisse la supposer...
D’Alembert.
Pour bien aborder ce chapitre
Ce chapitre est une introduction à l’une des plus fabuleuses invention de l’homme, celle du calcul différentiel, dans le cas des fonctions d’une variable réelle à valeurs réelles.
L’histoire du calcul différentiel débute en grande partie avec Galilée et Newton qui avaient besoin de nouveaux outils mathématiques pour développer les notions de vitesse et d’accélération d’un mouvement. Mais la possibilité de calculer la pente de la tangente à une courbe était essentielle dans d’autres problèmes comme dans ceux d’extremum ou pour des questions plus appliquées. Newton et Leibniz furent les premiers à tenter de formaliser la notion de dérivée. Ils se disputèrent la paternité de cette invention mais il semble certain maintenant qu’ils l’ont découvert de manière indépendante et chacun via des formalismes différents. Comme expliqué dans l’introduction du chapitre [chapitre_suites_reelles], la notion de limite n’a été développée que bien plus tard, au \(19^{\textrm{ ème}}\) siècle par Cauchy et Weierstrass aussi la formalisation de la dérivation par Newton et Leibniz souffrait de nombreuses lacunes. Newton refusa d’ailleurs de publier son travail et les écrits de Leibniz étaient obscurs et difficiles à comprendre. Lagrange, un siècle plus tard introduit le terme de dérivée ainsi que la notation \(f'\).
Après avoir défini ce qu’est une fonction dérivable ainsi que sa dérivée, nous démontrerons les règles de calcul des dérivées que vous connaissez depuis le lycée. Nous verrons en particulier que la dérivée permet d’approcher une fonction donnée par une fonction affine (voir le théorème page [DL1]). Nous nous intéresserons aux propriétés globales des fonctions dérivables. Le théorème de Rolle [Theo_de_Rolle] page [Theo_de_Rolle] et celui des accroissements finis [thm:TAF] page [thm:TAF] seront d’un usage constant en analyse. L’inégalité des accroissements finis [thm:IAF] page [thm:IAF] qui découle du théorème du même nom est une véritable machine à fabriquer des inégalités. Des accroissements finis découle aussi le caractère \(k\)-Lipschitzien des fonctions dérivables, ce qui permet d’appliquer à celles pour qui \(k\in\left]0,1\right[\) le très important théorème du point fixe [thm:0709115046] page [thm:0709115046]. Le théorème de dérivation de la bijection réciproque [derivee_non_nulle_implique_bij] page [derivee_non_nulle_implique_bij] permettra de justifier les démonstrations effectuées dans le chapitre sur les fonctions usuelles. Nous continuerons cette section par une étude des fonctions de classe \(\mathcal{C}^{n}\) et \(\mathcal{C}^{\infty}\) et nous la terminerons par une introduction aux fonctions convexes. Ce dernier outil servira aussi à construire de nombreuses inégalités.
Dérivée en un point, fonction dérivée
Dans tout ce paragraphe, \(I\) est un intervalle de \(\mathbb{R}\) non vide et non réduit à un point. Les fonctions considérées sont définies sur \(I\) et à valeurs réelles.
Définitions
(Taux d’accroissement). Soient \(f\in \mathscr F \left(I,\mathbb{R}\right)\) et \(a\in I\). On définit le taux d’accroissement de la fonction \(f\) au point \(a\) comme étant la fonction \(\Delta_{a,f}\) définie par \[\Delta_{a,f}: \left\{ \begin{array}{ccl} I\setminus \left\{ a \right\} & \longrightarrow & \mathbb{R} \newline x & \longmapsto & \dfrac{f(x)-f(a)}{x-a} \end{array} \right.\]
(Fonction dérivable à droite, à gauche ). Soient \(f\in \mathscr
F \left(I,\mathbb{R}\right)\), \(a\in I\) et \(\Delta_{a,f}\) le taux d’accroissement de \(f\) au point \(a\). On dit que
\(f\) est dérivable à droite au point \(a\) si et seulement si \(\Delta_{a,f}\) admet une limite finie quand \(x\) tend vers \(a\) à droite de \(a\).
\(f\) est dérivable à gauche au point \(a\) si et seulement si \(\Delta_{a,f}\) admet une limite finie quand \(x\) tend vers \(a\) à gauche de \(a\).
(Dérivée en un point). Soient \(f\in \mathscr F \left(I,\mathbb{R}\right)\) et \(a\in I\). On dit que \(f\) est dérivable au point \(a\) si et seulement si son taux d’accroissement \(\Delta_{a,f}\) possède une limite finie quand \(x\) tend vers \(a\). Cette limite s’appelle le nombre dérivée de \(f\) au point \(a\) et est noté: \[f'(a) \quad \textrm{ ou} \quad Df(a) \quad \textrm{ ou} \quad\dfrac{df}{dx}(a)\]
Pour un point \(a\) intérieur à \(I\) (c’est-à-dire tel qu’il existe \(\alpha>0\) vérifiant \(\left]a-\alpha,a+\alpha\right[\subset I\)) alors \(f\) est dérivable au point \(a\) si et seulement si on a simultanément :
\(f\) est dérivable à droite en \(a\),
\(f\) est dérivable à gauche en \(a\),
\(f'_d(a)= f'_g(a)\)
Soient \(\left(\alpha,\beta\right)\in \mathbb{R}^2\) et \(f: \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \alpha x + \beta \end{array} \right.\). \(f\) est dérivable en tout point \(a\) de \(\mathbb{R}\) et \(\forall a \in \mathbb{R}, \quad f'(a)=\alpha\).
La fonction \(f: \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \left|x\right| \end{array} \right.\) est dérivable sur \(\mathbb{R}^*\), dérivable à droite et à gauche en \(0\) mais pas dérivable en \(0\).
Par contre la fonction \(f: \left\{ \begin{array}{ccl} \mathbb{R}^+ & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \left|x\right| \end{array} \right.\) est dérivable sur \(\mathbb{R}_+\).
la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)= \begin{cases} \exp\left(-\dfrac{1}{x}\right) & \textrm{ si $x>0$}\\ 0 & \textrm{ si $x \leqslant 0$} \end{cases}\) est dérivable sur \(\mathbb{R}\).
La fonction racine carrée : \(f: \left\{ \begin{array}{ccl} \mathbb{R}_+ & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \sqrt x \end{array} \right.\) est dérivable sur \(\mathbb{R}_+^*\). En effet, si \(a\in\mathbb{R}_+^*\) et si \(x\in\mathbb{R}_+\setminus\left\{a\right\}\) alors \[\dfrac{\sqrt{x}-\sqrt{a}}{x-a}= \dfrac{\sqrt{x}-\sqrt{a}}{\left(\sqrt{x}-\sqrt{a}\right)\left(\sqrt{x}+\sqrt{a}\right)} = \dfrac{1}{\sqrt{x}+\sqrt{a}}\xrightarrow[x\rightarrow a]{} \dfrac{1}{2\sqrt{a}}\] par opérations sur les limites. Donc \(f\) est bien dérivable en \(a\) et \(f'\left(a\right)= \dfrac{1}{2\sqrt{a}}\). Par contre, cette fonction n’est pas dérivable à droite en \(0\). En effet, si \(x\in\mathbb{R}_+^*\), on a \[\dfrac{\sqrt{x}-\sqrt{0}}{x-0}=\dfrac{1}{\sqrt x} \xrightarrow[x\rightarrow 0^+]{} +\infty.\]
Interprétations de la dérivée
Interprétation géométrique
Soient \(f\in \mathscr F \left(I,\mathbb{R}\right)\) et \(a\in I\). Le plan étant ramené à un repère orthonormé, pour \(x \in I\setminus \left\{ a \right\}\), considérons la droite joignant les points \(A \left|\begin{matrix} a \\ f(a) \end{matrix} \right.\) et \(M \left|\begin{matrix} x \\ f(x) \end{matrix} \right.\). La pente de la droite \((AM)\) est donnée par \[\Delta_a(x)={\dfrac{f(x)-f(a)}{x-a}}\] Si la fonction \(f\) est dérivable au point \(a\in I\), cette pente a pour limite \(f'(a)\) quand \(x\) tend vers \(a\). Le vecteur de composante \(\left|\begin{matrix} 1 \\ \Delta_a(x) \end{matrix} \right.\) dirige la corde \((AM)\) et tend vers \(\left|\begin{matrix} 1 \newline f'(a) \end{matrix} \right.\). La droite passant par \(A\) et de pente \(f'(a)\) est donc tangente à la courbe d’équation \(y=f(x)\). C’est la position limite des cordes \((AM)\) quand \(M\) tend vers \(A\).
La tangente en \(a\) est horizontale si et seulement si \(f'(a)=0\).
Si \(f\) est continue en \(a\) et si \(\Delta_a(x) \xrightarrow[x\rightarrow a]{} \pm \infty\), les cordes \((AM)\) ont une position limite verticale encore appelée tangente à la courbe en \(A\).
Si \(f\) n’est pas dérivable en \(a\) mais si \(\Delta_a(x)\) possède des limites à gauche et à droite en \(a\), \(A\) est appelé point anguleux de la courbe. C’est un point qui possède deux demi-tangentes de pentes différentes.
Interprétation cinématique
Considérant \(f(t)\) comme l’abscisse à l’instant \(t\) d’un point en mouvement rectiligne, pour \(t\neq a\), \(\Delta_{a,f}(t)\) représente la vitesse moyenne entre les instants \(t\) et \(a\) et sa limite \(f'(a)\), notée aussi \(\stackrel{.}{f}(a)\) la vitesse instantanée à l’instant \(a\).
Interprétation analytique
Le théorème suivant permet de caractériser la dérivabilité en un point sans faire intervenir de division. Il sera généralisé en deuxième année pour des fonctions de plusieurs variables.
(Développement limité à l’ordre \(1\) d’une fonction dérivable). Soit \(f \in \mathscr F \left(I,\mathbb{R}\right)\). La fonction \(f\) est dérivable au point \(a\in I\) si et seulement si il existe \(\varepsilon:I
\rightarrow \mathbb{R}\) telle que \(\varepsilon(x) \xrightarrow[x\rightarrow a]{} 0\) et un réel \(c\) tel que \[\forall x\in I, \quad \boxed{f(x)=f(a)+c(x-a)+
\underbrace{(x-a)\varepsilon(x)}_{\underset{x \rightarrow a}{o}\left(x-a\right)}}\] On a alors \(c=f'(a)\).
Pour \(x \in I \setminus \{a\}\), \(\dfrac{f(x)-f(a)}{x-a} = c + \varepsilon(x) \xrightarrow[x \rightarrow a]{} c\) ce qui montre que \(f\) est dérivable au point \(a\) et que \(f'(a) = c\).
Supposons que \(f\) est dérivable en \(a\). Pour tout \(x\in I\setminus \left\{a\right\}\), posons \(\varepsilon\left(x\right)=\Delta_a\left(x\right) - f'\left(a\right)\). Comme \(f\) est dérivable en \(a\), \(\varepsilon\left(x\right) \xrightarrow[x\rightarrow a]{} 0\). Prolongeons alors par continuité \(\varepsilon\) en \(a\) en posant \(\varepsilon\left(a\right)=0\). Pour tout \(x\in I\), on a alors bien \(f(x)=f(a)+c(x-a)+ (x-a)\varepsilon(x)\) avec \(c=f'\left(a\right)\).
Dérivabilité et continuité
(Dérivabilité implique continuité ). Soient \(f \in \mathscr F \left(I,\mathbb{R}\right)\) et \(a\in I\). Si \(f\) est dérivable en \(a\) alors \(f\) est continue en \(a\).
Comme \(f\) est dérivable en \(a\), d’après la proposition [DL1], il existe une fonction \(\varepsilon : I \rightarrow \mathbb{R}\) vérifiant \(\varepsilon(x)
\xrightarrow[x\rightarrow a]{} 0\) et telle que \[\forall x\in I, \quad f(x)=f(a)+f'\left(a\right)(x-a)+ (x-a)\varepsilon(x).\] Comme \(\varepsilon\left(x\right)\xrightarrow[x\rightarrow 0]{}0\), par opérations sur les limites, \(f\left(x\right)
\xrightarrow[x\rightarrow 0]{} f\left(a\right)\) et \(f\) est bien continue en \(a\).
La réciproque est bien entendu fausse (par exemple \(f : \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \left|x\right|\) est continue en \(0\) mais pas dérivable en \(0\)).
Si \(f\) est dérivable à gauche en \(a \in I\) alors \(f\) est continue à gauche en \(a\).
Si \(f\) est dérivable à droite en \(a \in I\) alors \(f\) est continue à droite en \(a\).
Si \(f\) possède une dérivée à droite et une dérivée à gauche en \(a\) alors \(f\) est continue en \(a\).
Fonction dérivée
(Dérivabilité sur un intervalle). On dit qu’une fonction \(f\) est dérivable sur \(I\) si et seulement si elle est dérivable en tout point \(a \in I\). On définit alors la fonction dérivée \[f': \left\{ \begin{array}{ccl} I & \longrightarrow & \mathbb{R} \newline x & \longmapsto & f'(x) \end{array} \right.\] La fonction dérivée se note aussi \(Df\) ou \(\dfrac{df}{dx}\).
Si une fonction \(f\) est dérivable sur \(I\) alors elle est continue sur \(I\).
Opérations sur les dérivées
(Règles de calcul de dérivées). Soient deux fonctions \(f\) et \(g\) définies sur \(I\) et dérivables en un point \(a\in I\). On a les propriétés suivantes :
Soient deux réels \(\alpha,\beta\in\mathbb{R}\). La fonction \(\alpha f+\beta g\) est dérivable en \(a\) et \[\boxed{\left(\alpha f+\beta g\right)'\left(a\right)=\alpha f'\left(a\right)+\beta g'\left(a\right)}\]
La fonction \(fg\) est dérivable en \(a\) et \[\boxed{\left(fg\right)'\left(a\right)=f'\left(a\right)g\left(a\right)+f\left(a\right)g'\left(a\right)}\]
Si \(g\left(a\right)\neq 0\), alors il existe un voisinage du point \(a\) sur lequel la fonction \(g\) ne s’annule pas. La fonction \(1/g\) est alors définie au voisinage du point \(a\) et est dérivable en \(a\) avec \[\boxed{\left(\dfrac{1}{g}\right)'\left(a\right)=-\dfrac{g'\left(a\right)}{g^2\left(a\right)}}\]
Si \(g\left(a\right)\neq 0\), alors de la même façon que précédemment la fonction \(f/g\) est définie au voisinage de \(a\), est dérivable en \(a\) et \[\boxed{\left(\dfrac{f}{g}\right)'\left(a\right)=\dfrac{f'\left(a\right)g\left(a\right)-f\left(a\right)g'\left(a\right)}{ g^2\left(a\right)}}\]
Soit \(x \in I\setminus\left\{a\right\}\).
On a \[\dfrac{\left(\alpha f + \beta g\right)\left(x\right) - \left(\alpha f + \beta g\right)\left(a\right)}{x-a}=\alpha \dfrac{f\left(x\right)-f\left(a\right)}{x-a} + \beta \dfrac{g\left(x\right)-g\left(a\right)}{x-a} \xrightarrow[x\rightarrow a]{} \alpha f'\left(a\right)+\beta g'\left(a\right)\] par opérations sur les limites.
On a \[\dfrac{\left(fg\right)\left(x\right) - \left(fg\right)\left(a\right)}{x-a} = \dfrac{f\left(x\right)- f\left(a\right)}{x-a} g\left(x\right) + \dfrac{g\left(x\right) - g\left(a\right)}{x-a}f\left(a\right) \xrightarrow[x\rightarrow a]{} f'\left(a\right)g\left(a\right)+f\left(a\right)g'\left(a\right)\] par opérations sur les limites et parce que \(g\) étant dérivable en \(a\), elle est continue en \(a\) et du coup \(g\left(x\right)\xrightarrow[x\rightarrow a]{} g\left(a\right)\).
Soit \(V\) un voisinage de \(a\) tel que \(\forall x\in V\cap I,\quad g\left(x\right)\neq 0\). On a \[\dfrac{\dfrac{1}{g}\left(x\right) - \dfrac{1}{g}\left(a\right)}{x-a} = - \dfrac{g\left(x\right)-g\left(a\right)}{g\left(x\right)g\left(a\right)} \cdot \dfrac{1}{x-a}=- \dfrac{g\left(x\right)-g\left(a\right)}{x-a} \cdot \dfrac{1}{g\left(x\right)g\left(a\right)} \xrightarrow[x\rightarrow a]{} - g'\left(a\right) \cdot \dfrac{1}{\left(g\left(a\right)\right)^2}\] par opérations sur les limites et parce que \(g\) est dérivable en \(a\) et donc continue en \(a\). Du coup, \(g\left(x\right) \xrightarrow[x\rightarrow a]{} g\left(a\right)\).
Il suffit d’appliquer les deux points précédents à \(F=f\) et \(G=\dfrac{1}{g}\). \(G\) est dérivable en \(a\) comme inverse d’une fonction dérivable en \(a\) et qui ne s’annule pas en \(a\) et \(F\) est dérivable en \(a\) car \(f\) l’est. \(FG\) est alors dérivable en \(a\) comme produit de fonctions dérivables en \(a\). De plus, \[\left(FG\right)'\left(a\right) = F'\left(a\right)G\left(a\right) + F\left(a\right)G'\left(a\right) = \dfrac{f'\left(a\right)}{g\left(a\right)} - \dfrac{f\left(a\right) g'\left(a\right) }{g^2\left(a\right)} = \dfrac{f'\left(a\right) g\left(a\right) - f\left(a\right)g'\left(a\right)}{g^2\left(a\right)}\]
(Théorème d’opérations sur les fonctions dérivables). Soient \(f\) et \(g\) deux fonctions définies et dérivables sur \(I\).
Soit \((\alpha,\beta)\in\mathbb{R}^2\). La fonction \(\alpha f+\beta g\) est dérivable sur l’intervalle I et \[\boxed{\left(\alpha f+\beta g\right)'=\alpha f'+\beta g'}\]
La fonction \(fg\) est dérivable sur l’intervalle \(I\) et \[\boxed{\left(fg\right)'=f'g+fg'}\]
Si la fonction \(f\) ne s’annule pas sur \(I\), alors la fonction \(1/f\) est définie et dérivable sur \(I\) avec \[\boxed{\left(\dfrac{1}{f}\right)'=-\dfrac{f'}{f^2}}\]
Si la fonction \(g\) ne s’annule pas sur \(I\) alors la fonction \(f/g\) est dérivable sur l’intervalle \(I\) et \[\boxed{\left(\dfrac{f}{g}\right)'=\dfrac{f'g-fg'}{ g^2}}\]
Ces propriétés sont vraies en chaque point de \(I\) et donc sur \(I\) tout entier.
(Dérivation des fonctions composées). Soient deux fonctions \(f:I \rightarrow R\), \(g:J \rightarrow \mathbb{R}\) telles que \(f(a)\in J\). On suppose que
Alors la fonction \(g\circ f\) est dérivable en \(a\) et \[\boxed{\left(g\circ f\right)'\left(a\right)= g'\left(f\left(a\right)\right) \times f'\left(a\right)}\]
La fonction \(f\) est dérivable au point \(a\in I\).
La fonction \(g\) est dérivable au point \(b=f(a)\in J\).
Introduisons la fonction \[h: \left\{ \begin{array}{ccl} J & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \begin{cases}
\dfrac{g\left(y\right)-g\left(b\right)}{y-b} &\textrm{ si } y\neq b \newline g'\left(y\right) &\textrm{ si } y=
b \end{cases} \end{array} \right.\] qui est continue en \(b\) car \(g\) est dérivable en \(b\). Alors pour tout \(x\in I\setminus\left\{a\right\}\) :
\[\dfrac{g\left(f\left(x\right)\right)- g\left(f\left(a\right)\right)}{x-a} = h\left(f\left(x\right)\right)\dfrac{f\left(x\right)-f\left(a\right)}{x-a}
\xrightarrow[x\rightarrow a]{} h\left(b\right) \times f'\left(a\right)= g'\left(f\left(a\right)\right) \times f'\left(a\right)\] par opérations sur les limites.
Dans cette preuve, on pourrait être tenter d’écrire pour \(x\in
I\setminus \left\{ a\right\}\) \[\dfrac{g\circ f\left(x\right) -
g\circ f\left(a\right)}{x-a} = \dfrac{g\left(f\left(x\right)\right) - g\left(f\left(a\right)\right)}{f\left(x\right)-f\left(a\right)}
\dfrac{f\left(x\right)-f\left(a\right)}{x-a}\] ce qui n’est pas correct car la fonction \(f\) peut s’annuler une infinité de fois au voisinage de \(a\) sans être constante et tout en étant dérivable en \(a.\) Un exemple d’une telle fonction est donné par \(x\mapsto x^2 \sin 1/x\) en \(a=0\).
Soient deux fonctions \(f:I \rightarrow R\) et \(g:J \rightarrow \mathbb{R}\) telles que \(f(I)\subset J\). On suppose que
Alors la fonction \(g\circ f\) est dérivable sur \(I\) et \[\boxed{\left(g\circ f\right)'= (g'\circ {f}) \times f'}\]
La fonction \(f\) est dérivable sur \(I\).
La fonction \(g\) est dérivable sur \(J\)
La propriété est vraie en chaque point de \(I\) donc elle est vraie sur \(I\).
(Dérivation de la bijection réciproque). Soit une fonction \(f:I \rightarrow R\). On suppose que
Alors la fonction \(f\) réalise une bijection de l’intervalle \(I\) sur l’intervalle \(J=f(I)\) et son application réciproque, \(f^{-1}\) est dérivable sur l’intervalle \(J\) avec \[\boxed{\left(f^{-1}\right)'=\dfrac{1}{f'\circ f^{-1}}}\]
la fonction \(f\) est injective sur l’intervalle \(I\).
la fonction \(f\) est dérivable sur l’intervalle \(I\).
la fonction \(f'\) ne s’annule pas sur \(I\) : \(\forall x\in I, \quad \boxed{f'\left(x\right)\neq 0}\).
Comme \(f\) est injective sur \(I\), elle est bijective de \(I\) sur \(J\) et comme elle est dérivable sur \(I\) elle est continue sur \(I\) et \(J\) est un intervalle de \(\mathbb{R}\). En appliquant le théorème [theo_bij_continue], sa bijection réciproque \(f^{-1}\) est continue sur \(J\). Soit \(y_0\in J\). Montrons que la fonction \(f^{-1}\) est dérivable au point \(y_0\). Soit \(y\in J\setminus
\left\{y_0\right\}\). Écrivons : \[\Delta_{y_0, f^{-1}}(y) = \dfrac{f^{-1}(y) - f^{-1}(y_0)}{y-y_0} =
\dfrac{1}{\dfrac{f(f^{-1}(y)) - f(f^{-1}(y_0))}{f^{-1}(y)-f^{-1}(y_0)}} =
\dfrac{1}{\Delta_{f^{-1}(y_0), f}(f^{-1}(y))}\] Puisque la fonction \(f\) est dérivable au point \(f^{-1}(y_0)\), \(\Delta_{f^{-1}(y_0), f}(y) \xrightarrow[y \rightarrow y_0]{} f'(f^{-1}(y_0))\). Puisque cette limite est non nulle, par opération sur les limites, \(\Delta_{y_0, f^{-1}}(y) \xrightarrow[y \rightarrow y_0]{} 1/f'(f^{-1}(y_0))\).
Soient \(n\in \mathbb{N}^*\) et \(f_n:x \mapsto x^n\). \(f_n\) est une bijection strictement croissante de \(\mathbb{R}_+^*\) sur \(\mathbb{R}_+^*\). Sa dérivée n’est jamais nulle. La fonction réciproque \(g_n\) de \(f_n\) est donc dérivable sur \(\mathbb{R}_+^*\) et \(g_n: \left\{ \begin{array}{ccl} \mathbb{R}_+^* & \longrightarrow & \mathbb{R}_+^* \\ y & \longmapsto & \sqrt[n]{x} \end{array} \right.\) vérifie, \[\forall y \in \mathbb{R}_+^*, \quad g_n'\left(y\right)=\dfrac{1}{n\left(\sqrt[n]{y}\right)^{n-1}}\]
La fonction \(f: \left\{ \begin{array}{ccl} ]-\dfrac{\pi}{2},\dfrac{\pi}{2}[ & \longrightarrow & ]-1,1[ \\ x & \longmapsto & \sin x \end{array} \right.\) est une bijection strictement croissante et sa dérivée n’est jamais nulle. La fonction réciproque, \(\operatorname{arcsin} : \left\{ \begin{array}{ccl} ]-1,1[ & \longrightarrow & ]-\dfrac{\pi}{2},\dfrac{\pi}{2}[ \newline y & \longmapsto & \operatorname{arcsin} y \end{array} \right.\) est dérivable sur \(]-1,1[\) et \[\forall y \in ]-1,1[,\quad \operatorname{arcsin} '(y)=\dfrac{1}{\sqrt{1-y^2}}\]
Étude globale des fonctions dérivables
Extremum d’une fonction dérivable
(Condition nécessaire d’un extremum relatif). Soit \(f\) une fonction définie sur un intervalle \(I\) de \(\mathbb{R}\) et soit \(a\) un point de \(I\) tel que
alors \(\boxed{f'(a)=0}\).
Le point \(a\) est intérieur à l’intervalle, c’est-à-dire qu’il existe \(\alpha >0\) tel que \(]a-\alpha, a+\alpha[ \subset I\).
Le point \(a\) est un extremum local de la fonction \(f\) sur \(I\).
La fonction \(f\) est dérivable au point \(a\).
Quitte à changer \(f\) en \(-f\), on peut supposer que \(f\) possède un maximum local en \(a\), c’est-à-dire qu’il existe \(\beta>0\) tel que \(\forall
x\in\left[a-\beta,a+\beta\right]\cap I,\quad f\left(x\right)\leqslant f\left(a\right)\). Posons \(r=\min\left(r_1,r_2\right)\).
Si \(a-r < x < a\), \([f(x)-f(a)]/(x-a) \leqslant 0\). Puisque \([f(x)-f(a)]/(x-a) \xrightarrow[x \rightarrow a]{} f'_g(a)\), par passage à la limite dans l’inégalité, on tire que \(f'_d\left(a\right)\leqslant 0\).
Si \(a<x<a+r\), \([f(x)-f(a)]/(x-a) \geqslant 0\) et puisque \([f(x)-f(a)]/(x-a) \xrightarrow[x \rightarrow a]{} f'_d(a)\), par passage à la limite dans l’inégalité, on obtient que \(f'_d(a) \geqslant 0\).
Puisque \(f\) est dérivable en \(a\), on obtient que \(f'_g\left(a\right) = f'_d\left(a\right)=f'\left(a\right)=0\).
La condition \(f'(a)=0\) n’est pas une condition suffisante d’extremum, (penser à \(f: x \mapsto x^3\) en \(x=0\).)
La condition \(a\) est intérieur à l’intervalle est fondamentale dans ce théorème. Si le point \(a\) est une borne de l’intervalle, on ne peut obtenir qu’une inégalité sur la dérivée à gauche ou à droite au point \(a\).
Théorème de Rolle
(Théorème de Rolle). Soit \(f:\left[a,b\right] \rightarrow \mathbb{R}\). On suppose que
Alors il existe \(c\in\left]a,b\right[\) tel que \(\boxed{f'\left(c\right)=0}\).
la fonction \(f\) est continue sur le segment \(\left[a,b\right]\),
la fonction \(f\) est dérivable sur l’intervalle ouvert \(\left]a,b\right[\),
\(f\left(a\right)=f\left(b\right)\).
Comme \(f\) est continue sur le segment \(\left[a,b\right]\), l’image de ce segment, par application du théorème [image_segment_appl_continue] est un segment \(\left[m,M\right]\) avec \(m\leqslant M\).
Si \(m=M\) alors \(f\) est constante sur \(\left[a,b\right]\) et sa dérivée est nulle sur \(\left]a,b\right[\).
Sinon, alors \(m<M\). Comme \(f\left(a\right)=f\left(b\right)\) l’un des deux est différent de \(m\) ou \(M\). On peut supposer que \(f\left(a\right) \neq m\). Le minimum de \(f\) sur \(\left[a,b\right]\) est donc atteint en un point \(c\in \left[a,b\right]\) différent de \(a\) et de \(b\), donc en un point intérieur de l’intervalle \([a,b]\). D’après la proposition précédente, on a \(f'\left(c\right)=0\).
Interprétation graphique
Interprétation cinématique
Un point mobile sur un axe qui revient à sa position de départ a vu sa vitesse s’annuler à un instant donné.
appendice analyse pour l’utilisation pratique du théorème de Rolle, polynômes, extremum d’une bonne fonction auxiliaire
Égalité des accroissements finis
(Théorème des accroissement finis (TAF)). Soit une fonction \(f:\left[a,b\right] \rightarrow \mathbb{R}\). On suppose que
Alors il existe un point intérieur \(c\in\left]a,b\right[\) tel que \[\boxed{f(b)-f(a)=f'(c)\left(b-a\right)}\]
la fonction \(f\) est continue sur le segment \(\left[a,b\right]\),
la fonction \(f\) est dérivable sur l’intervalle ouvert \(\left]a,b\right[\).
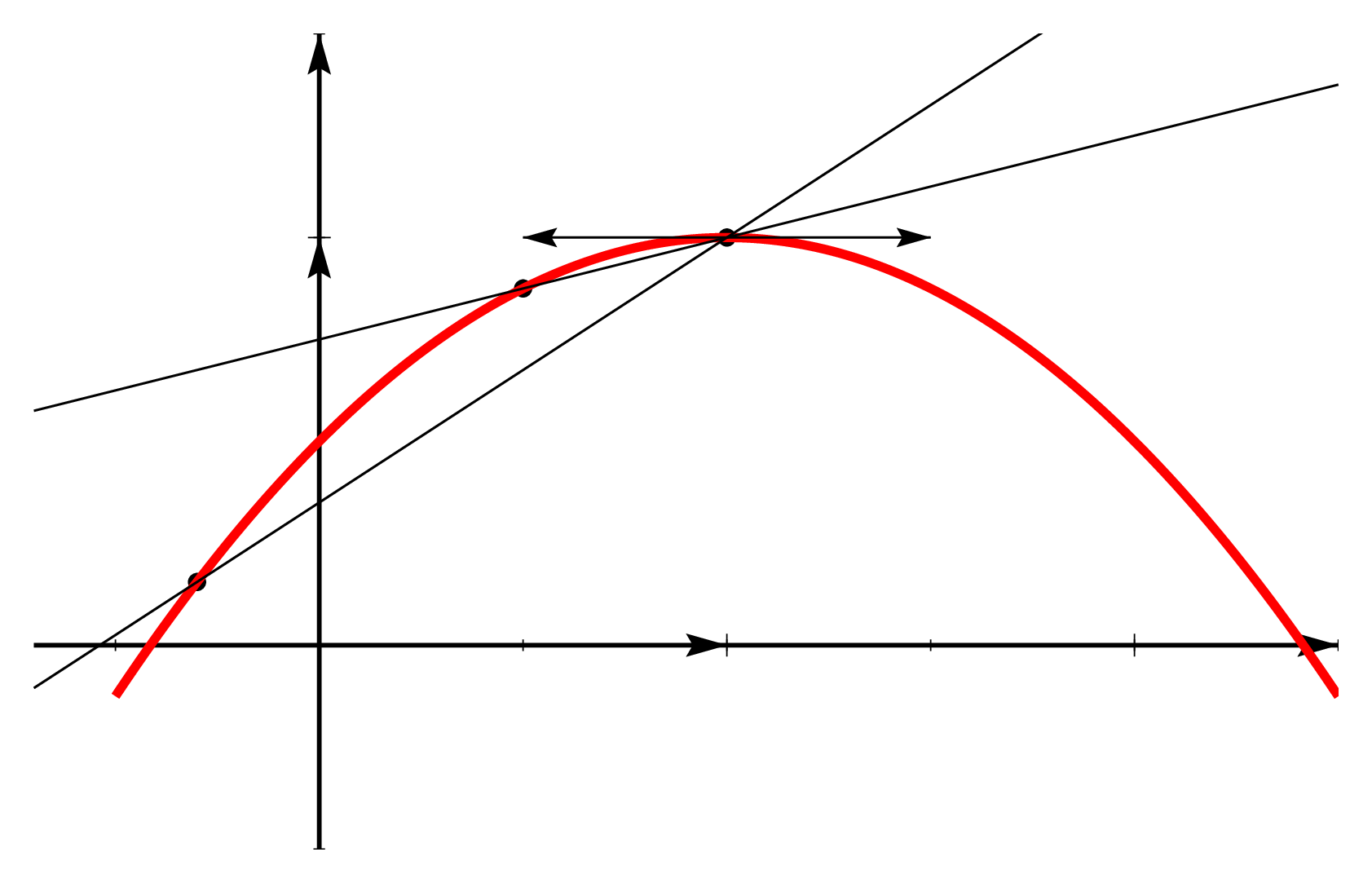
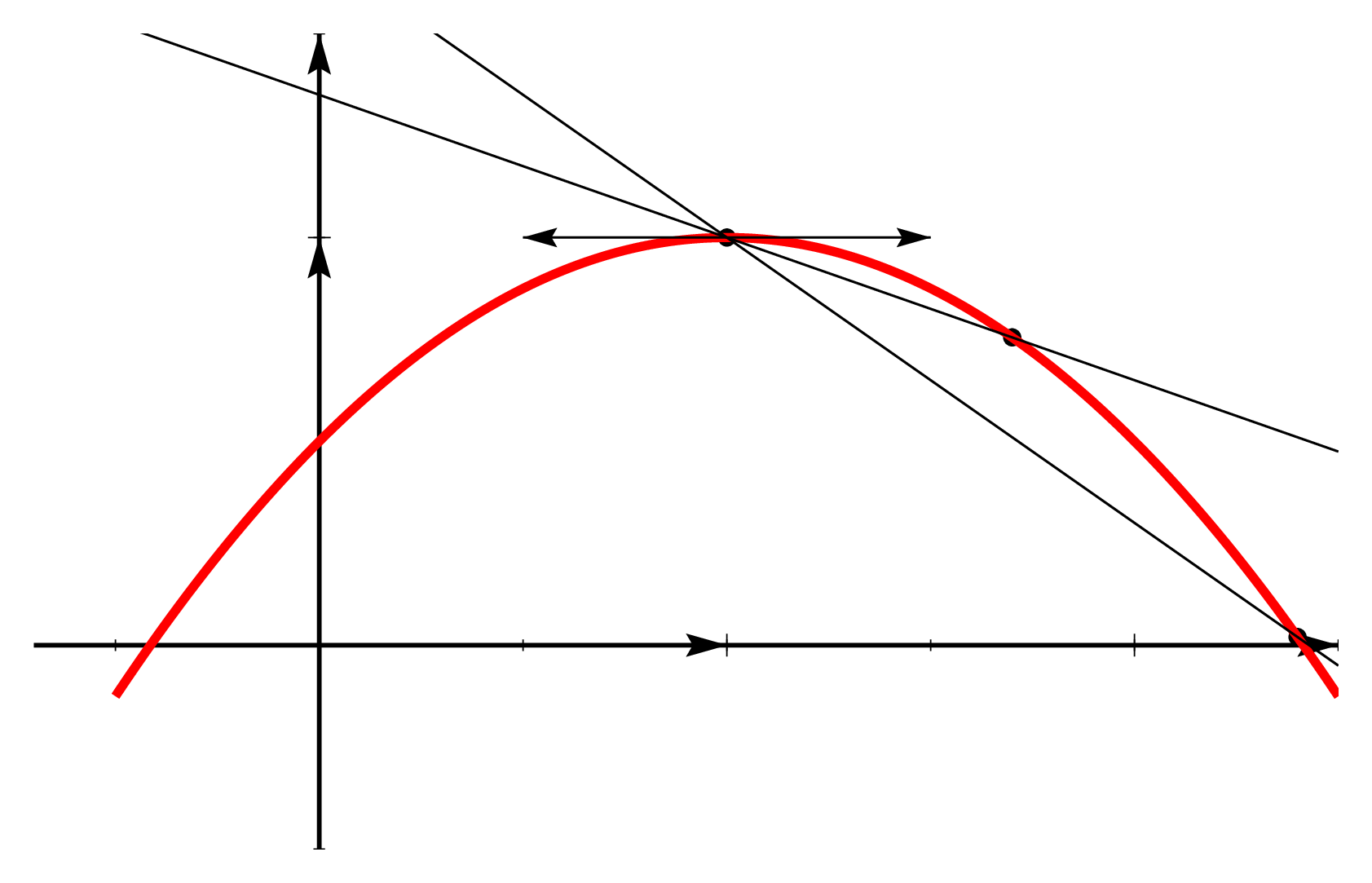
Nous allons donner deux preuves typiques dont on s’inspire dans les exercices. L’idée consiste à appliquer le théorème de Rolle à une bonne fonction auxiliaire pour obtenir l’existence du réel \(c\) vérifiant la propriété qui nous intéresse. La première preuve consiste à voir sur un dessin un problème d’extremum.
(1). En examinant la figure ci-dessus, on voit que le point \(c\) correspond au maximum de l’écart vertical entre la corde \([A,B]\) et le point \((x, f(x))\). Définissons donc la mesure algébrique de cet écart : \[\varphi: \left\{ \begin{array}{ccl} [a,b] & \longrightarrow & \mathbb{R} \newline x & \longmapsto & f(x) - \left[f(a) + \dfrac{f(b)-f(a)}{b-a}(x-a)\right] \end{array} \right.\] La fonction \(\varphi\) est continue sur le segment \([a, b]\) (théorèmes généraux), dérivable sur l’intervalle \(]a, b[\) (théorème généraux sur les dérivées) et on calcule \(\varphi(a) = \varphi(b) = 0\). D’après le théorème de Rolle, il existe un point intérieur \(c \in ]a, b[\) tel que \(\varphi'(c) = 0\), c’est-à-dire \(f'(c) - \dfrac{f(b)-f(a)}{b-a} = 0\).
La deuxième preuve est plus taupinale et peu naturelle, mais fournit une recette qui fonctionne bien dans les exercices lorsque la formule à démontrer est compliquée.
Dans la formule à démontrer, regrouper tous les \(c\) à un endroit et les remplacer par une constante \(K\).
Remplacer l’une des bornes (par exemple \(b\)) par une variable \(t\), ce qui fournit une fonction auxiliaire \(\varphi\) définie sur \([a, b]\).
Déterminer la constante \(K\) de telle sorte que \(\varphi(a) = \varphi(b)\).
Appliquer le théorème de Rolle à cette fonction auxiliaire.
(1). Appliquons cette recette à notre problème. La formule à montrer s’écrit \(f(b) - f(a) - f'(c)(b-a) = 0\). Définissons donc une fonction auxiliaire \(\varphi: \left\{ \begin{array}{ccl} [a,b] & \longrightarrow & \mathbb{R} \newline x & \longmapsto & f(t)-f(a) - K(t-a) \end{array} \right.\) où \(K\) est une constante que nous choisissons de telle sorte que \(\varphi(a)=\varphi(b)\). On trouve que \(K = [f(b)-f(a)]/(b-a)\) ce qui conduit à la fonction auxiliaire de la première preuve.
Cette méthode d’un usage très courant est très employée dans les exercices
Quand un mobile se déplace sur un axe et part d’un point \(A\) au temps \(t_1\), arrive en \(B\) au temps \(t_2\) et si \(f\) est la fonction position de ce mobile sur l’axe, alors il existe un instant \(t\in\left]t_1,t_2\right[\) tel que la vitesse instantanée en \(t\) : \(f'\left(t\right)\) de ce mobile soit égale à sa vitesse moyenne \(\dfrac{f\left(t_2\right)-f\left(t_1\right)}{t_2-t_1}\).
Inégalité des accroissements finis
(Inégalité des accroissement finis (IAF)). Soit une fonction \(f:\left[a,b\right] \rightarrow \mathbb{R}\). On suppose que
Alors on a \[\boxed{m\left(b-a\right)\leqslant f(b)-f(a)\leqslant M\left(b-a\right)}\]
la fonction \(f\) est continue sur le segment \(\left[a,b\right]\),
la fonction \(f\) est dérivable sur l’intervalle ouvert \(\left]a,b\right[\),
il existe deux réels \((m,M)\in \mathbb{R}^2\) tel que \(\forall x \in ]a,b[, \quad m \leqslant f'(x) \leqslant M\).
Il suffit d’appliquer le théorème des accroissements finis à la fonction \(f\) sur le segment \(\left[a,b\right]\). Il existe un réel \(c\in\left]a,b\right[\) tel que \(f(b)-f(a)=f'(c)\left(b-a\right)\). Puisque \(m \leqslant f'(x) \leqslant M\), on en déduit que \(m\left(b-a\right)\leqslant f(b)-f(a)\leqslant M\left(b-a\right)\).
(Dérivée bornée implique lipschitzienne). Soit une fonction \(f:I \rightarrow \mathbb{R}\) définie sur un intervalle \(I\). On suppose que
Alors la fonction \(f\) est \(K\)-lipschitzienne sur l’intervalle \(I\).
la fonction \(f\) est continue sur l’intervalle \(I\),
la fonction \(f\) est dérivable sur l’intervalle ouvert \(\overset{\circ}{I}\),
la fonction \(f\) est bornée sur l’intervalle ouvert \(\overset{\circ}{I}\) : \(\exists K \geqslant 0\), tel que \(\forall x \in \overset{\circ}{I}\), \(\lvert f'(x) \rvert \leqslant K\).
Soit \((x, y) \in I^2\) avec \(x<y\). Puisque \([x, y] \subset I\), la fonction \(f\) est continue sur le segment \([x,y]\) et dérivable sur l’intervalle ouvert \(]x, y[\), d’après le théorème des accroissements finis, il existe \(c \in ]x, y[\) tel que \(f(y)-f(x) = f'(c)(y-x)\). On en déduit que \(\lvert f(y)-f(x) \rvert = \lvert f'(c) \rvert \lvert y-x \rvert \leqslant K\lvert y-x \rvert\).
Application: Variations d’une fonction
Le résultat suivant, utilisé depuis le lycée est une conséquence du théorème des accroissements finis.
(Caractérisation des fonctions constantes, monotones). Soit une fonction \(f : I \mapsto \mathbb{R}\). On suppose que
\(f\) est dérivable sur \(I\).
Alors on a les résultats suivants :
\(\left[\forall x\in I, \quad f'(x) \geqslant 0 \right]\Longleftrightarrow f\) est croissante sur \(I\).
\(\left[\forall x\in I, \quad f'(x) > 0\right]\) \(\Rightarrow\) \(f\) est strictement croissante sur \(I\).
\(\left[\forall x\in I, \quad f'(x) \leqslant 0 \right]\Longleftrightarrow f\) est décroissante sur \(I\).
\(\left[\forall x\in I, \quad f'(x) < 0 \right]\) \(\Rightarrow\) \(f\) est strictement décroissante sur \(I\).
\(\left[\forall x\in I, \quad f'(x) = 0\right] \Longleftrightarrow f\) est constante sur \(I\).
Démontrons la première équivalence. Les trois suivantes se démontrent de même.
Supposons que : \(\forall x\in ]a,b[\subset I, \quad f'(x) \geqslant 0\) et montrons que \(f\) est croissante sur \([a,b]\). Soient \(x_1,x_2 \in\left[a,b\right]\) tels que \(x_1 < x_2\). \(f\) est continue sur \(\left[x_1,x_2\right]\) et dérivable sur \(\left]x_1,x_2\right[\). D’après le théorème des accroissements finis, il existe \(c\in \left]x_1,x_2\right[\) tel que \(f\left(x_2\right)-f\left(x_1\right) = f'\left(c\right) \left(x_2 - x_1\right)\geqslant 0\) et donc \(f\left(x_2\right) \geqslant f\left(x_1\right)\) ce qui prouve que \(f\) est croissante.
Réciproquement, supposons que \(f\) est croissante sur \([a,b]\). Alors, pour tout \(x_0\in \left]a,b\right[\) le taux d’accroissement de \(f\) en \(x_0\), \(\Delta_{x_0,f}\) est une fonction positive sur \(\left]a,b\right[ \setminus \left\{x_0\right\}\). Puisque la fonction \(f\) est dérivable au point \(x_0\), \(\Delta_{x_0,f}(x) \xrightarrow[x \rightarrow x_0]{} f'(x_0)\). Par passage à la limite dans l’inégalité, on en tire que \(f'\left(x_0\right)\geqslant 0\).
La réciproque de (2) est fausse : la fonction \(x \mapsto x^3\) est strictement croissante sur \(\mathbb{R}\), dérivable et pourtant sa dérivée s’annule en \(0\).
Condition suffisante de dérivabilité en un point
(Théorème du prolongement dérivable). Soit une fonction \(f:I \rightarrow \mathbb{R}\) et un réel \(a\in I\). On suppose que
Alors la fonction \(f\) est dérivable au point \(a\) et \(f'(a)=l\).
la fonction\(f\) est continue sur l’intervalle \(I\),
la fonction \(f\) est dérivable sur \(I\setminus\left\{a\right\}\),
\(f'(x) \xrightarrow[x\rightarrow a]{} l\in \mathbb{R}\).
Soit \(x\in I\setminus\left\{a\right\}\). La formule des accroissements finis appliquée au segment \(\left[a,x\right]\) nous assure de l’existence de \(c_x\in\left]a,x\right[\) tel que \(\dfrac{f\left(x\right)-f\left(a\right)}{x-a}=f'\left(c_x\right)\). Comme \(c_x
\xrightarrow[x\rightarrow a^+]{}a\), on en déduit que \(\dfrac{f\left(x\right)-f\left(a\right)}{x-a}
\xrightarrow[x\rightarrow a^+]{}l\) et donc que \(f\) est dérivable à droite en \(a\) et que \(f_d'(a)=l\). On fait de même à gauche de \(a\).
Soient \(f:I \rightarrow \mathbb{R}\) et \(a\in I\). On suppose que
Alors \(\displaystyle{\lim_{x \rightarrow a}\dfrac{f(x)-f(a)}{x-a}}=+\infty\). En d’autres termes, la courbe représentative de \(f\) possède une tangente verticale au point \(a\).
la fonction \(f\) est continue sur \(I\),
la fonction \(f\) est dérivable sur \(I\setminus\left\{a\right\}\),
\(f'(x) \xrightarrow[x\rightarrow a]{} +\infty\).
Laissée au lecteur en s’inspirant par exemple de la preuve de la proposition précédente.
(1). La réciproque du théorème de prolongement dérivable est fausse comme le montre le contre-exemple suivant \[f : \left\{ \begin{array}{ccl} \mathbb{R} & \longrightarrow & \mathbb{R} \\ x & \longmapsto & \begin{cases} x^2\sin\dfrac{1}{x} & \textrm{
si } x \neq 0 \newline
0 & \textrm{ si } x = 0
\end{cases}
\end{array} \right.\] Cette fonction est dérivable en \(0\) et \(f'(0) = 0\) car \[\Bigl| \dfrac{f(x) - f(0)}{x}\Bigr| \leqslant\lvert x \rvert \lvert \sin{\scriptstyle 1\over\scriptstyle x} \rvert
\leqslant\lvert x \rvert \xrightarrow[x \rightarrow 0]{} 0\] La fonction \(f\) est dérivable en tout point \(x \neq 0\) avec \(f'(x) = 2x\sin(1/x) - \cos(1/x)\) et \(f'\) n’admet pas de limite lorsque \(x \rightarrow 0\). En effet, la suite \(\left(f\left(1/(n\pi)\right)\right)_{n\geqslant 1}\) admet deux sous-suites, une convergeant vers \(1\) et l’autre vers \(-1\).
Dérivées successives
Dérivée seconde
Soit une fonction \(f\) définie et dérivable sur un intervalle \(I\) de \(\mathbb{R}\).
(Fonction deux fois dérivable). On dit que la fonction \(f\) est deux fois dérivable sur \(I\) lorsque la fonction \(f'\) est dérivable en tout point de \(I\). Sa dérivée est appelée fonction dérivée seconde de \(f\) et est notée \[f'' \quad \textrm{ ou} \quad D^2f \quad \textrm{ ou} \quad\dfrac{d^2f}{dt^2}\]
Si \(f\) est deux fois dérivable sur \(I\) alors \(f'\) et \(f\) sont continues sur \(I\).
Lorsque \(f(t)\) est l’abscisse à l’instant \(t\) d’un point en mouvement rectiligne alors \(f''(t)\), si elle existe, représente l’accélération de ce point à l’instant \(t\).
Dérivée d’ordre \(n\)
Soit \(n\in \mathbb{N}\).
(Dérivées successives). Étant donné une fonction \(f:I\rightarrow \mathbb{R}\), on pose \(f^{(0)}=f\) et on définit par récurrence, la dérivée \(n^{\textrm{ ème}}\) de \(f\) sur \(I\), notée \(f^{(n)}\), comme la dérivée de \(f^{(n-1)}\), si elle existe. On la note \[f^{(n)} \quad \textrm{ ou} \quad D^n f \quad \textrm{ ou} \quad\dfrac{d^n f}{dt^n}\]
L’existence de \(f^{(n)}\) sur \(I\) entraîne l’existence et la continuité, sur \(I\), de toutes les dérivées d’ordre strictement inférieur.
Si \(f\) est \(n\) fois dérivable sur \(I\) alors \(f=f^{\left(0\right)}\), \(f'=f^{\left(1\right)}\), \(\dots\), \(f^{\left(n-1\right)}\) sont continues sur \(I\).
Étant donné deux fonctions \(f\) et \(g\) définies sur \(I\) et \(n\) fois dérivables sur \(I\) ainsi que deux réels \(\alpha\) et \(\beta\). Alors la fonction \(\alpha f + \beta g\) est elle aussi \(n\) fois dérivable sur \(I\) et : \[\forall x\in I, \quad \boxed{
\left(\alpha f+\beta g\right)^{(n)}\left(x\right)=\alpha f^{(n)}\left(x\right)+\beta
g^{(n)}\left(x\right)}\]
Par récurrence.
Gottfried Leibniz, Né le 1er juillet \(1646\) à Leipzig , mort le \(14\) novembre \(1716\) à Hanovre Gottfried Leibniz est un philosophe, scientifique, mathématicien, diplomate, bibliothécaire et juriste allemand. Il se montre précoce intellectuellement et possède de fortes capacités d’apprentissage. Il dit avoir appris seul le latin et à \(15\) ans il connaît la littérature grecque et latine. Il obtient son baccalauréat à \(17\) ans et rentre la même année à l’Université de Leipzig où il étudie la philosophie, le droit et les mathématiques. Cette université lui refuse en \(1666\) de lui décerner le titre de docteur, sans doute à cause de son très jeune âge et il obtient celui-ci un an plus tard à l’Université de Nuremberg. Plutôt que de chercher un poste universitaire, il rentre au service du baron von Boyneburg à Francfort qui l’initie à la politique. Leibniz est, avec Newton, l’inventeur du calcul infinitésimal et fut le découvreur des formules de dérivation d’un produit, d’un quotient et d’une puissance. Newton était parvenu de son côté, quelques années auparavant, aux mêmes résultats que Leibniz mais sans publier son travail. Une longue polémique s’ensuivit afin de déterminer qui avait la paternité de cette théorie.
(Formule de Leibniz). Si \(f\) et \(g\) sont deux fonctions \(n\) fois dérivables sur \(I\) alors il en est du même du produit \(fg\) et on a la formule de Leibniz qui permet d’exprimer la dérivée \(n\)-ième du produit \[\boxed{\left(fg\right)^{(n)}=\displaystyle{\sum_{k=0}^n \dbinom{n}{k}
f^{(k)}g^{(n-k)}}}\]
Par récurrence. Voir la preuve de la formule du binôme de Newton [formule_du_binome].
Soient \(f:I \rightarrow \mathbb{R}\) et \(g:J \rightarrow \mathbb{R}\) telles que \(f(I)\subset J\). Soit \(n\in \mathbb{N}^*\). Si
Alors la fonction composée \(g\circ f\) est \(n\) fois dérivable sur l’intervalle \(I\).
la fonction \(f\) est \(n\) fois dérivable sur l’intervalle \(I\),
la fonction \(g\) est \(n\) fois dérivable sur l’intervalle \(J\).
Par récurrence sur \(n\). Pour \(n = 1\), la propriété a déjà été montrée. Soit \(n\in\mathbb{N}^*\). Supposons qu’une composée de fonctions \(n\) fois dérivable est \(n\) fois dérivable sur \(I\). Montrons que si \(f\) et \(g\) sont \((n+1)\) fois dérivable sur \(I\) et \(J\) respectivement alors \(g\circ f\) est \(n+1\) fois dérivable sur \(I\). On sait que \(f\) et \(g\) sont \(1\) fois dérivable sur respectivement \(I\) et \(J\) et que \((f\circ g)' =
f' \times g'\circ f\). D’après l’hypothèse de récurrence, comme \(f'\) et \(g'\) sont \(n\) fois dérivables sur \(I\) et \(J\) respectivement, \(g'\circ f\) est \(n\) fois dérivable sur \(I\) et d’après le théorème de Leibniz, \(f' \times g'\circ f\) est aussi \(n\) fois dérivable sur \(I\). Donc \(\left(g\circ f\right)'\) est \(n\) fois dérivable sur \(I\) et \(g\circ f\) est \((n+1)\) fois dérivable sur \(I\). La propriété est ainsi prouvée par récurrence.
Une expression de la dérivée \(n\)-ième de la composée de deux fonctions est donnée par la formule de Faà di Bruno. Elle est très difficile à manipuler et ne relève pas du programme.
Fonctions de classe \(\mathcal{C}^{n}\)
Soit \(n\in \mathbb{N}\).
(Fonctions de classe \(\mathcal{C}^{n}\)). On dit qu’une fonction \(f:I \rightarrow \mathbb{R}\) est de classe \(\mathcal{C}^{n}\) sur l’intervalle \(I\) si et seulement si
\(f\) est \(n\) fois dérivable sur \(I\),
la fonction \(f^{(n)}\) est continue sur \(I\).
On note
\(\mathcal{C}^{0}\left(I\right)\) l’ensemble des fonctions de classe \(\mathcal{C}^{0}\) sur \(I\), c’est-à-dire l’ensemble des fonctions continues sur \(I\).
Pour \(n\geqslant 1\), \(\mathcal{C}^{n}\left(I\right)\) l’ensemble des fonctions de classe \(\mathcal{C}^{n}\) sur \(I\).
\(\mathcal{C}^{+\infty}\left(I\right)\) l’ensemble des fonctions indéfiniment dérivables sur \(I\).
Soit \((f,g)\in \mathcal{C}^{n}\left(I\right)^2\) et soit \(\left(\alpha,\beta\right) \in \mathbb{R}^2\). Alors
\(\alpha f+\beta g \in \mathcal{C}^{n}\left(I\right)\)
\(fg \in \mathcal{C}^{n}\left(I\right)\)
La première égalité et le fait que la fonction nulle est de classe \(\mathcal{C}^{n}\) permet d’affirmer que \(\mathcal{C}^{n}\left(I\right)\) est un sous-espace vectoriel de \(\mathscr F\left(I,\mathbb{R}\right)\) (Voir la définition [def_sous-ev] page [def_sous-ev]).
On a \[\dots\subset \mathcal{C}^{n}\left(I\right) \subset \mathcal{C}^{n-1}\left(I\right) \subset \dots\mathcal{C}^{2}\left(I\right) \subset \mathcal{C}^{1}\left(I\right) \subset \mathcal{C}^{0}\left(I\right) \subset \mathscr F\left(I,\mathbb{R}\right)\]
Soient \(f:I \rightarrow \mathbb{R}\) et \(g:J \rightarrow \mathbb{R}\) telles que \(f(I)\subset J\). Soit \(n\in \mathbb{N}\). Si
alors \(g\circ f\in \mathcal{C}^{n}\left(I\right)\).
\(f\in \mathcal{C}^{n}\left(I\right)\),
\(g\in \mathcal{C}^{n}\left(J\right)\),
Soient \(n\in \mathbb{Z}\) et \(f_n: \left\{ \begin{array}{ccl} \mathbb{R}^* & \longrightarrow & \mathbb{R} \newline x & \longmapsto & x^n \end{array} \right.\). On a pour tout \(n\in
\mathbb{Z},\quad f_n \in \mathcal{C}^{\infty}\left(\mathbb{R}^*\right)\) ( On a même \(f_n \in
\mathcal{C}^{ \infty}\left(\mathbb{R}\right)\) si \(n\in\mathbb{N}\)).
Soit \(f\in \mathcal{C}^{n}\left(I\right)\) ne s’annulant pas sur \(I\), alors \(1/f\) est élément de \(\mathcal{C}^{n}\left(I\right)\).
(Théorème de la bijection de classe \(\mathcal{C}^{n}\)). Soit \(f\in \mathcal{C}^{n}\left(I\right)\) telle que
alors \(f\) est une bijection sur son image \(J=f(I)\) et \(f^{-1}\) est de classe \(\mathcal{C}^{n}\) sur \(J\).
\(f'\) ne s’annule pas sur \(I\).
Fonctions convexes
(Fonction convexe). Soit \(f:I\mapsto \mathbb{R}\) une fonction définie sur un intervalle \(I\subset \mathbb{R}\). On dit que \(f\) est convexe lorsque \[\forall (x,y)\in I^2, \forall \lambda \in [0,1], \quad
f\bigl(\lambda x + (1-\lambda)y\bigr) \leqslant
\lambda f(x) + (1-\lambda)f(y)\]
Cela signifie géométriquement que le graphe de \(f\) est situé en dessous de toutes les cordes joignant deux points de ce graphe.
On dit qu’une fonction \(f\) définie sur un intervalle \(I\) est concave lorsque \[\forall (x,y)\in I^2, \forall \lambda \in [0,1], \quad
f\bigl(\lambda x + (1-\lambda)y\bigr) \geqslant
\lambda f(x) + (1-\lambda)f(y)\] La fonction \(f\) est concave si et seulement si la fonction \(-f\) est convexe. Dans la suite, on n’étudiera que les propriétés des fonctions convexes.
Les fonctions qui sont à la fois convexes et concaves sont les fonctions affines.
(Fonction strictement convexe). On dit qu’une fonction \(f: I \mapsto \mathbb{R}\) est strictement convexe lorsque \(\forall (x, y)\in I^2\), \(x \neq y\), \[\forall \lambda \in ]0, 1[,\quad f\bigl(\lambda x + (1-\lambda) y \bigr)
< \lambda f(x) + (1-\lambda) f(y)\]
(Inégalité de convexité généralisée). Soit une fonction \(f\) convexe sur l’intervalle \(I\). Alors \[\forall n\geqslant 2, \forall (x_1,\dots,x_n)\in I^n, \forall
(\lambda_1,\dots,\lambda_n)\in [0,1]^n \textrm{ tels que } \sum_{i=1}^n
\lambda_i=1\] \[f(\lambda_1x_1+\dots+\lambda_nx_n) \leqslant\lambda_1f(x_1)+\dots +
\lambda_n f(x_n).\]
Par récurrence sur \(n\). Pour \(n = 2\), c’est la définition d’une fonction convexe. Montrons \(\mathcal{P}(n) \Rightarrow \mathcal{P}(n+1)\). Soient \(x_1,\dots, x_n, x_{n+1} \in I\) et \(\lambda_1,\dots \lambda_{n+1} \in [0, 1]\) tels que \(\sum_{i=1}^{n+1} \lambda_i = 1\). On peut supposer que tous les \(\lambda_i\) sont strictement positifs, sinon on se ramène à la propriété \(\mathcal{P}(n)\). Posons \(y=\dfrac{\sum_{i=1}^n \lambda_i x_i
}{\sum_{i=1}^n \lambda_i}\) et pour \(i \in [\kern-0.127em[ 1, n ]\kern-0.127em]\), \(\mu_i = \dfrac{\lambda_i}{\sum_{i=1}^n \lambda_i}\) : \(\sum_{i=1}^n
\mu_i = 1\). Puisque \(f\) est convexe, \[f(\lambda_{n+1} x_{n+1} + (1-\lambda_{n+1})y) \leqslant\lambda_{n+1}
f(x_{n+1}) + (1-\lambda_{n+1}) f(y)\] et d’après \(\mathcal{P}(n)\), \[f(y) = f(\mu_1 x_1 + \dots + \mu_n x_n) \leqslant\mu_1 f(x_1) + \dots +
\mu_n f(x_n)\] En utilisant que \(1-\lambda_{n+1} = \sum_{i=1}^n \lambda_i\), on obtient \[(1-\lambda_{n+1}) f(y) \leqslant\lambda_1 f(x_1) + \dots + \lambda_n
f(x_n)\] d’où l’inégalité souhaitée.
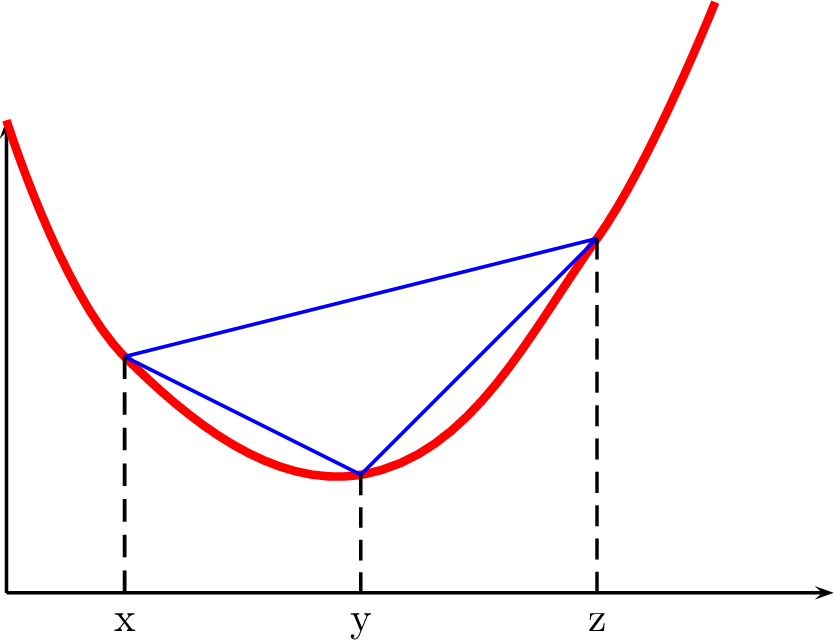
Le résultat suivant est à la base de toutes les démonstrations et est souvent utilisé dans les exercices théoriques sur les fonctions convexes. Il est facile à retenir, il suffit de faire le schéma suivant :
(Lemme des trois pentes). Soit \(f:I\mapsto \mathbb{R}\) une fonction convexe : \[\forall (x,y,z)\in I^3,~x<y<z, \quad\dfrac{f(y)-f(x)}{y-x}
\leqslant\dfrac{f(z)-f(x)}{z-x}
\leqslant\dfrac{f(z)-f(y)}{z-y}\]
Puisque \(x < y < z\), \(y\) peut s’écrire comme barycentre de \(x\) et \(z\) : il existe \(\lambda \in [0, 1]\) tel que \(y
= \lambda x + (1-\lambda) z\). Après calculs, on trouve que \[\lambda = \dfrac{z-y}{z-x}\] Puisque \(f\) est convexe, \[f(y) \leqslant\lambda f(x) + (1-\lambda) f(z)\] On en tire que \[f(y) - f(x) \leqslant(1-\lambda) \bigl(f(z)-f(x)\bigr)\] et comme \(1-\lambda = \dfrac{y-x}{z-x}\), que \[\dfrac{f(y)-f(x)}{y-x} \leqslant\dfrac{f(z)-f(x)}{z-x}\] De même, \[f(y) - f(z) \leqslant\lambda \bigl(f(x) - f(z)\bigr)\] d’où \[\lambda\bigl(f(z)-f(x)\bigr) \leqslant f(z)-f(y)\] et donc \[\dfrac{z-y}{z-x}\bigl(f(z)-f(x)\bigr) \leqslant f(z)-f(y)\] d’où l’on tire \[\dfrac{f(z)-f(x)}{z-x} \leqslant\dfrac{f(z)-f(y)}{z-y}\]
Le théorème suivant fournit un moyen très pratique de montrer qu’une fonction est convexe : il suffit de montrer que sa dérivée seconde est positive sur \(I\).
(Caractérisation des fonctions convexes dérivables).
Si \(f:I\mapsto \mathbb{R}\) est dérivable, \[(f\textrm{ convexe }) \Longleftrightarrow (f' \textrm{ croissante })\]
Si \(f:I\mapsto \mathbb{R}\) est deux fois dérivable, \[(f \textrm{ convexe }) \Longleftrightarrow (f'' \geqslant 0 \textrm{ sur } I )\]
Si \(f\) est convexe et dérivable, soient \(x < y\) deux points de \(I\). Montrons que \(f'(x) \leqslant f'(y)\). Soit \(z \in ]x, y[\), d’après le lemme des trois pentes, \[\dfrac{f(z)-f(x)}{z-x} \leqslant\dfrac{f(y)-f(x)}{y-x}\] En passant à la limite dans l’inégalité lorsque \(z \rightarrow x^+\), on trouve que \(f'(x) \leqslant\dfrac{f(y)-f(x)}{y-x}\). On a également \[\dfrac{f(y)-f(x)}{y-x} \leqslant\dfrac{f(y)-f(z)}{y-z}\] et en passant à la limite dans l’inégalité lorsque \(z \rightarrow y^{-}\), \(\dfrac{f(y)-f(x)}{y-x} \leqslant f'(y)\). Finalement, \[f'(x) \leqslant\dfrac{f(y)-f(x)}{y-x} \leqslant f'(y)\]
Supposons réciproquement \(f\) dérivable et \(f'\) croissante. Soient \(x < y\) deux points de \(I\) et \(\lambda \in [0, 1]\). Posons \(z = \lambda x + (1-\lambda)y\). D’après le théorème des accroissements finis entre \(x\) et \(z\), il existe \(c_1 \in ]x, z[\) tel que \[\dfrac{f(z)-f(x)}{z-x} = f'(c_1)\] De même, le théorème des accroissements finis entre \(z\) et \(y\) garantit l’existence de \(c_2 \in ]z, y[\) tel que \[\dfrac{f(y)-f(z)}{y-z} = f'(c_2)\] Puisque \(f'\) est croissante, \(f'(c_1) \leqslant f'(c_2)\) d’où l’on tire \[\dfrac{f(z)-f(x)}{z-x} \leqslant\dfrac{f(y)-f(z)}{y-z}\] En remplaçant \(z\) par sa valeur, on aboutit alors à l’inégalité de convexité \[f(\lambda x + (1-\lambda) y) \leqslant\lambda f(x) + (1-\lambda) f(y)\]
Si \(f\) est deux fois dérivable, on sait que la fonction \(f'\) est croissante si et seulement si la fonction \(f''\) est positive.
(Le graphe d’une fonction convexe est situé au dessus de toutes ses tangentes). Soit une fonction \(f:I\mapsto \mathbb{R}\) convexe et dérivable. \[\forall x_0\in I,~\forall x\in I, \quad f(x) \geqslant f(x_0)+f'(x_0)(x-x_0)\]
Si \(x_0 < x\), prenons \(z \in ]x_0, x[\) et utilisons le lemme des trois pentes : \[\dfrac{f(z)-f(x_0)}{z-x_0} \leqslant\dfrac{f(x)-f(x_0)}{x-x_0}\] En passant à la limite dans l’inégalité lorsque \(z \rightarrow x_0\), on en tire que \[f'(x_0) \leqslant\dfrac{f(x)-f(x_0)}{x-x_0}\] d’où \(f(x) \geqslant(x-x_0)f'(x_0) + f(x_0)\).
Si \(x < x_0\), on prend \(z \in ]x, x_0[\) et avec le lemme des trois pentes, \[\dfrac{f(x_0)-f(x)}{x_0-x} \leqslant\dfrac{f(x_0)-f(z)}{x_0-z}\] En passant à la limite dans l’inégalité lorsque \(z \rightarrow x_0\), on trouve \[\dfrac{f(x_0)-f(x)}{x_0-x} \leqslant f'(x_0)\] et l’on retrouve que \(f(x) \geqslant f(x_0) - (x_0-x)f'(x_0)\).
Multimédia: tangente qui varie, lemme des 3 pentes
On obtient des inégalités intéressantes, dites inégalités de convexité de la façon suivante :
On se donne une fonction \(f\) ;
On vérifie qu’elle est convexe sur \(I\) en vérifiant que \(f'' \geqslant 0\) ;
On écrit l’inégalité de convexité (éventuellement généralisée).
(Exemples d’inégalités de convexité).
Si \(\alpha \geqslant 1\) et \(x, y > 0\), \((x+y)^{\alpha} \leqslant 2^{\alpha-1} (x^{\alpha} + y^{\alpha})\).
Pour \(n\) réels \(x_1,\dots, x_n\), \((x_1+\dots + x_n)^2 \leqslant n (x_1^2 + \dots + x_n^2)\).
Considérons la fonction \(f : \left\{ \begin{array}{ccl} ]0,+\infty[ & \longrightarrow & \mathbb{R} \\ x & \longmapsto & x^{\alpha} \end{array} \right.\). Elle est deux fois dérivable sur \(I = ]0, +\infty[\) et \(\forall x > 0\), \(f''(x) = \alpha(\alpha-1)x^{\alpha-2} \geqslant 0\). C’est donc une fonction convexe. En prenant \(\lambda = 1/2\), on en déduit que \(\forall x, y > 0\), \((\dfrac{x+y}{2})^{\alpha} \leqslant \dfrac{x^{\alpha} + y^{\alpha}}{2}\) d’où la première inégalité.
La fonction \(x \mapsto x^2\) est convexe sur \(\mathbb{R}\) et il suffit d’utiliser l’inégalité de convexité généralisée avec \(\lambda_1 = \dots = \lambda_n = 1/n\) : \[\left( \dfrac{x_1+\dots + x_n}{n}\right)^2 \leqslant\dfrac{x_1^2+\dots + x_n^2}{n}\] d’où la deuxième inégalité.
(Concavité du logarithme).
Comparaison entre moyenne géométrique et arithmétique. Pour tous réels \(x_1,\dots, x_n > 0\) : \[(x_1\dots x_n)^{1/n} \leqslant\dfrac{x_1+\dots + x_n}{n}\]
Inégalité de Young : pour deux réels \(a, b >0\) et deux réels \(p, q > 0\) vérifiant \(\dfrac{1}{p} + \dfrac{1}{q} = 1\), \[ab \leqslant\dfrac{a^p}{p} + \dfrac{b^q}{q}\]
En notant \(f : x \mapsto \ln x\), \(f''(x) = -1/x^2 \leqslant 0\) donc la fonction logarithme est concave sur \(]0, +\infty[\).
En utilisant l’inégalité de convexité généralisée avec \(\lambda_1=\dots=\lambda_n=1/n\), \[\ln\Bigl(\dfrac{x_1+\dots + x_n}{n}\Bigr) \geqslant\dfrac{\ln x_1 + \dots + \ln x_n}{n} = \ln \left((x_1\dots x_n)^{1/n}\right)\] En prenant l’exponentielle (qui est une fonction croissante), on en déduit l’inégalité souhaitée.
Pour \(\lambda \in [0, 1]\) et \(x, y > 0\), \[\ln(\lambda x + (1-\lambda) y) \geqslant\lambda \ln x + (1-\lambda) \ln y = \ln(x^{\lambda}y^{1-\lambda})\] d’où en prenant l’exponentielle, \[x^{\lambda}y^{1-\lambda} \leqslant\lambda x + (1-\lambda) y\] Il suffit alors de prendre \(x = a^p\), \(y=b^q\) et \(\lambda = 1/p\) pour trouver l’inégalité de Young.
En résumé
Les différents théorèmes de ce chapitre doivent être parfaitement connus. Il est du plus mauvais effet d’oublier de vérifier une des hypothèses du théorème de Rolle ou de celui des accroissement finis dans une démonstration. A ce stade de l’année, les calculs de dérivée doivent être menés sans hésitation et les formules de dérivation doivent être connues à la perfection. On complétera la lecture du chapitre par celle du paragraphe [AnnexeC_derivees] page [AnnexeC_derivees] de l’annexe [AnnexeC] qui traite des méthodes de calcul des dérivées. Enfin, il est intéressant de maîtriser la démonstration du théorème du point fixe [thm:0709115046] page [thm:0709115046]. Nombreux sont les exercices qui n’en sont qu’un cas particulier.
Bibliographie
Barre utilisateur
[ID: 67] [Date de publication: 10 décembre 2021 17:32] [Catégorie(s): Le cours de SUP ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]Commentaires sur le cours
Documents à télécharger
L'article complet