Compared to what an ellipse can tell us, a circle has nothing to say.
Eric T. Bell.
Pour bien aborder ce chapitre
Les-mathematiques.net
Les-mathematiques.net
Les-mathematiques.net
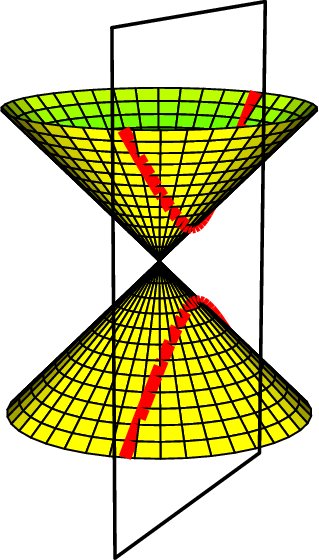
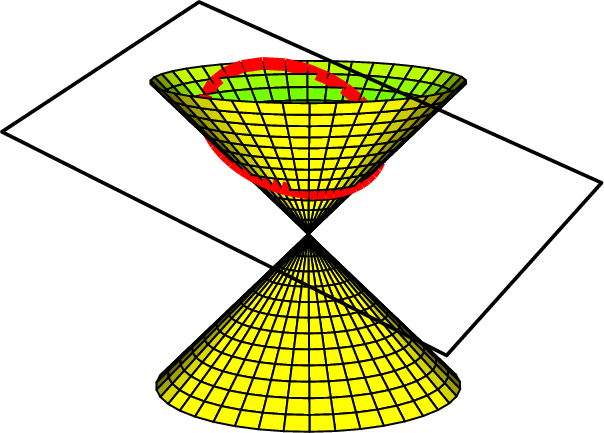
Les coniques sont des courbes du plan étudiées depuis les grecs. Elles l’ont été par Menechme vers \(400\) ans avant J.C. Puis par Archimède, Apollonius de Perge, ... Ils les voyaient comme les intersections d’un cône et d’un plan et les avaient baptisées sections coniques. Suivant l’angle d’inclinaison de ce plan avec l’axe du cône, on distingue différents cas (voir l’exercice [exo_coniques_comme_section_plan_cône] page [exo_coniques_comme_section_plan_cône]) :
Si cet angle est inférieur à l’angle d’ouverture du cône, on obtient une hyperbole.
Si cet angle est supérieur à l’angle d’ouverture du cône, on obtient une ellipse.
Si cet angle est égal à l’angle d’ouverture du cône, on obtient une parabole.
Mais d’autres situations peuvent se produire, ainsi si le plan contient le sommet du cône, l’intersection du plan et du cône peut être formé de deux droites sécantes, ou d’une seule droite, ou même seulement de ce sommet. Ces coniques sont dites dégénérées tandis que les trois premières obtenues sont dites propres.
Il existe d’autres façons d’introduire les coniques. Celle retenue dans ce cours est appelée définition monofocale des coniques, ou définition par foyer-directrice (voir la définition [def_monofocale_conique]). On verra, avec la définition bifocale (voir la définition [def_bifocale_conique]) un autre moyen de définir les coniques propres.
Enfin, on peut voir les coniques comme la famille des courbes du plan d’équation cartésienne \(a x^2 + 2 b xy +c y^2 + dx+ey+f=0\) où \(a,b,c,d,e,f\in\mathbb{R}\). On apprendra dans le paragraphe [para_courbes_algebriques_plans] à étudier de telles courbes et comment reconnaître parmi celles-ci les coniques propres.
Les coniques possèdent de nombreuses propriétés géométriques remarquables et on en étudiera quelques unes dans les exercices de ce chapitre. On les retrouve en mains endroits dans la nature. Kepler au \(16^{\textrm{ e}}\) siècle a compris que les planètes décrivent des ellipses dont le soleil occupe un des deux foyers. Galilée au \(17^{\textrm{ e}}\) siècle découvre qu’un obus tiré d’un canon décrit une trajectoire parabolique. La trajectoire d’une comète cyclique est une ellipse et celle d’une comète qui ne revient jamais est une parabole ou une hyperbole. Dans la vie courante, c’est grâce aux propriétés géométriques des paraboles que peuvent fonctionner les télescopes et les antennes paraboliques (voir l’exercice [exo_telescope] page [exo_telescope]).
Définitions et premières propriétés
Définition monofocale
Si \(A\) et \(B\) sont deux points du plan, on notera \(d\left(A,B\right)\) la distance de \(A\) à \(B\), c’est-à-dire la norme du vecteur \(\overrightarrow{AB}\).
(Conique). Soient \(\mathscr D\) une droite du plan, \(F\) un point du plan n’appartenant pas à \(\mathscr D\) et \(e\) un réel strictement positif. On appelle conique de foyer\(F\), de directrice\(\mathscr D\) et d’excentricité\(e\) la courbe \(\mathscr C\) formée des points \(M\) du plan vérifiant: \[\boxed{d(M,F)=e~d(M,\mathscr D)}\]
Si \(0<e<1\), on dit que \(\mathscr C\) est une ellipse.
Si \(e=1\), on dit que \(\mathscr C\) est une parabole.
Si \(e>1\), on dit que \(\mathscr C\) est une hyperbole.
La droite \(\Delta\) passant par \(F\) et orthogonale à \(\mathscr D\) est appelée l’axe focal.
L’axe focal d’une conique est un axe de symétrie de cette conique.
Les-mathematiques.net
Soit \(M\) un point de la conique \(\mathscr C\) de directrice \(\mathscr D\), de foyer \(F\) et d’excentricité \(e\). Soit \(\Delta\) l’axe focal de \(\mathscr C\) et soit \(M'\) l’image de \(M\) par la réflexion d’axe \(\Delta\). Soit \(H\) et \(H'\) les projetés orthogonaux respectifs de \(M\) et \(M'\) sur \(\mathscr D\). Les droites \(\mathscr D\) et \(\Delta\) sont perpendiculaires donc \(d\left(M',\mathscr D\right)=H'M'=HM=d\left(M,\mathscr D\right).\) Comme \(\Delta\) est la médiatrice du segment \(\left[MM'\right]\) et que \(F\in\Delta\), on a aussi \(d\left(M',F\right)=d\left(M,F\right)\). Par conséquent \(d\left(M',F\right) = d\left(M,F\right) = e d\left(M,\mathscr D\right)=e d\left(M',\mathscr D\right)\) ce qui prouve que \(M'\in\mathscr C\).
(Paramètre). Soit \(\mathscr C\) une conique de directrice \(\mathscr D\), de foyer \(F\) et d’excentricité \(e\). Soit \(d=d(F,\mathscr D)\). Le réel \(p=e~d\) est appelé paramètre de la conique \(\mathscr C\).
Le paramètre d’une conique \(\mathscr C\) correspond à la distance de \(F\) à chacun des deux points de \(\mathscr C\) situés sur la droite passant par \(F\) et parallèle à \(\mathscr D\).
Équation cartésienne d’une conique
Les-mathematiques.net
(Équation cartésienne d’une conique). Soit \(\mathscr C\) une conique de directrice \(\mathscr D\), de foyer \(F\) et d’excentricité \(e\). Soit \(d=d(F,\mathscr D)\)· Dans un repère orthonormal \((F,\overrightarrow{i}, \overrightarrow{j})\) choisi en sorte que \(\mathscr D\) ait pour équation \(x=-d\) (\(\Longleftrightarrow\overrightarrow{i}\) unitaire normal à \(\mathscr D\) et \(\overrightarrow{j}\) unitaire directeur pour \(\mathscr D\)) \(\mathscr C\) a pour équation cartésienne: \[\boxed{x^2 + y^2 = e^2 (x+d)^2}\]
Soit \(K\) le projeté orthogonal de \(F\) sur la directrice \(\mathscr D\). On rapporte le plan au repère \(\mathscr R\left(F,\overrightarrow{i}, \overrightarrow{j}\right)\) où \(\overrightarrow{i}={\scriptstyle\overrightarrow{KF}\over\scriptstyle\left\|\overrightarrow{KF}\right\|}\) et où \(\overrightarrow{j}\) est directement orthogonal à \(\overrightarrow{i}\). Remarquons que \(\overrightarrow{j}\) dirige la directrice \(\mathscr D\). Posons \(d=d(F,\mathscr D)\)· La directrice, dans ce repère, admet bien comme équation cartésienne \(x=-d\). Soit \(M \left|\begin{matrix} x \\ y \end{matrix} \right.\). On a : \[\begin{aligned}
M \in \mathscr C &\Longleftrightarrow& d(M,F)=e~d(M,\mathscr D)\\
&\Longleftrightarrow& d^2(M,F)=e^2~d^2(M,\mathscr D)\newline
&\Longleftrightarrow& x^2+y^2=e^2 \left(x+d\right)^2\end{aligned}\] d’où l’équation cartésienne de la conique dans \(\mathscr R\).
L’axe focal de la conique passe par \(F\) et est dirigé par \(\overrightarrow{i}\). Son équation dans \(\mathscr R\) est \(y=0\).
Multimédia: Pour une directrice et un foyer fixés, on trace en faisant varier \(e\) les différentes coniques correspondantes.
Équation polaire d’une conique
On fixe un repère orthonormal du plan \(\left(O,\overrightarrow{i},\overrightarrow{j}\right)\).
(Équation polaire d’une conique). Soit \(\mathcal D\) la droite d’équation polaire \(r=\dfrac{d}{\cos\left(\theta-\theta_0\right)}\) avec \(h\neq 0\). Alors une équation polaire de la conique \(\mathscr C\) de foyer \(O\), d’excentricité \(e\) et de directrice \(\mathcal D\) est : \[\boxed{r=\dfrac{ed}{1+e\cos\left(\theta-\theta_0\right)}}.\]
Si \(\theta_0=\pi~\left[2\pi\right]\) alors la directrice \(\mathcal D\) est perpendiculaire à l’axe des abscisses et d’équation \(x=-d\). On peut alors utiliser la proposition [rep_conique] : une équation cartésienne de \(\mathscr C\) est \(x^2+y^2=e^2\left(x+d\right)^2\). On passe en polaire et on obtient \(r=\pm e\left(r\cos \theta +d\right)\). La conique \(\mathscr C\) est donc l’ensemble des points satisfaisant :\[r=-\dfrac{ed}{1+e\cos \theta} \textrm{ ou }
r=\dfrac{ed}{1-e\cos \theta}.\] Mais ces deux équations sont celles d’une même courbe. En effet, si \(\left(r,\theta\right)\) satisfait la première équation alors \(\left(-r,\theta+\pi\right)\) satisfait la seconde. Ces deux couples sont les coordonnées polaires d’un même point du plan. Une équation polaire de \(\mathscr
C\) est donc donnée par \(r=\dfrac{ed}{1+e\cos \left(\theta-\pi\right)}\).
Dans le cas général, on effectue une rotation de centre \(O\) et d’angle \(\theta_0-\pi\) et on trouve pour la conique l’équation polaire \(r=\dfrac{ed}{1+e\cos\left(\theta-\theta_0\right)}\).
L’équation polaire d’une conique s’écrit aussi \(p=\dfrac{p}{1+e\cos\left(\theta-\theta_0\right)}\)
L’axe focal de cette conique admet comme équation polaire \(\theta=\theta_0\).
Étude de la parabole: \(e=1\)
On s’intéresse dans ce paragraphe à une parabole \(\mathscr P\) de foyer \(F\), de directrice \(\mathscr D\), de paramètre \(p>0\). On considère à nouveau le repère \(\mathscr R(F,\overrightarrow{i}, \overrightarrow{j})\) construit dans la proposition [rep_conique]. Dans ce repère, une équation de \(\mathscr P\) est \[x^2 + y^2 = (x+p)^2.\] L’axe focal \(\Delta\), passe par \(F\), est dirigé par \(\overrightarrow{i}\) (et admet donc comme équation \(y=0\)), coupe \(\mathscr P\) en un unique point de coordonnées \((-{\scriptstyle p\over\scriptstyle 2},0)\), ce qui justifie la définition suivante:
(Sommet d’une parabole). On appelle sommet de la parabole \(\mathscr P\) l’unique point \(S\) d’intersection entre \(\mathscr P\) et son axe focal \(\Delta\). Dans le repère \((F,\overrightarrow{i}, \overrightarrow{j})\), les coordonnées de \(S\) sont \((-{\scriptstyle p\over\scriptstyle 2},0)\).
Si \(K\) est le projeté orthogonal de \(F\) sur \(\mathscr D\), \(S\) est le milieu de \([FK]\).
(Équation réduite d’une parabole). Il existe un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) dans lequel la parabole \(\mathscr P\) de paramètre \(p>0\) admet pour équation caractéristique: \[\boxed{Y^2-2~p~X=0}\] Cette équation est appelée équation réduite de la parabole \(\mathscr P\).
Réciproquement, une courbe d’équation : \(Y^2-2~p~X=0\) dans un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) est une parabole de foyer \(\boxed{F \left|\begin{matrix} {\scriptstyle p\over\scriptstyle 2} \newline 0 \end{matrix} \right.}\) et de directrice d’équation \(\boxed{\mathscr D~:X=-{\scriptstyle p\over\scriptstyle 2}}\).
Les-mathematiques.net
Soit \(\mathscr P\) la parabole de paramètre \(p>0\), de foyer \(F\) et de directrice \(\mathscr D\). Dans le repère \(\mathscr R\left(F,\overrightarrow{i},\overrightarrow{j}\right)\) construit dans la proposition [rep_conique], \(\mathscr P\) admet comme équation cartésienne \(x^2 + y^2 = (x+p)^2\) ou :\(y^2 = 2px +p^2\). Considérons le point \(O\left(-{\scriptstyle p\over\scriptstyle 2},0\right)\) et le repère \(\mathscr R'\left(O,\overrightarrow{i},\overrightarrow{j}\right)\). Calculons les formules de changement de coordonnées du repère \(\mathscr R\) au repère \(\mathscr R'\). Soit \(M\) un point du plan de coordonnées \(\left(x,y\right)\) dans \(\mathscr R\) et de coordonnées \(\left(X,Y\right)\) dans \(\mathscr R'\). On a : \[\overrightarrow{OM}=X \overrightarrow{i} + Y \overrightarrow{j}.\] Par ailleurs : \[\overrightarrow{OM} = \overrightarrow{OF} + \overrightarrow{FM}
= {\scriptstyle p\over\scriptstyle 2} \overrightarrow{i} + x\overrightarrow{i} + y \overrightarrow{j} = \left(x+{\scriptstyle p\over\scriptstyle 2}\right)\overrightarrow{i} + y \overrightarrow{j}.\] Par identification, on obtient alors : \[\begin{cases}
X = x+\dfrac{p}{2}\\
Y=y
\end{cases}.\] L’équation de \(\mathscr P\) : \(y^2 = 2px +p^2\) devient dans \(\mathscr R'\) : \(Y^2 =
2pX\). Remarquons que \(O\) est le sommet de la parabole.
Soit \(\mathscr C\) une courbe d’équation \(Y^2-2~p~X=0\) dans un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\). Montrons que \(\mathscr C\) est une parabole. Soit \(\mathscr D\) la droite d’équation \(X=-{\scriptstyle p\over\scriptstyle 2}\), \(F \left|\begin{matrix} {\scriptstyle p\over\scriptstyle 2} \\ 0 \end{matrix} \right.\) et \(M \left|\begin{matrix} X \\ Y \end{matrix} \right.\) un point du plan. Montrons que \(d\left(M,F\right)=d\left(M,\mathscr D\right)\) si et seulement si \(M\in\mathscr C\) ce qui prouvera que \(\mathscr C\) est une parabole \(\mathscr P\) de foyer \(F\) et de directrice \(\mathscr D\). Remarquons que : \[d^2\left(M,F\right)= \left(X-{\scriptstyle p\over\scriptstyle 2}\right)^2 + Y^2 \quad \textrm{ et} \quad
d^2\left(M,\mathscr D\right)= \left(X+{\scriptstyle p\over\scriptstyle 2}\right)^2.\] On a : \[\begin{aligned}
M\in\mathscr P &\Longleftrightarrow& d\left(M,F\right) = d\left(M,\mathscr D\right)\\
&\Longleftrightarrow& d^2\left(M,F\right) = d^2\left(M,\mathscr D\right)\\
&\Longleftrightarrow& \left(X-\dfrac{p}{2}\right)^2+ Y^2= \left(X+\dfrac{p}{2}\right)^2\\
&\Longleftrightarrow& Y^2-2~p~X=0\newline
&\Longleftrightarrow& M\in\mathscr C.\end{aligned}\]
(Paramétrage de la parabole). On peut paramétrer la parabole d’équation \(Y^2-2~p~X=0\) dans un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) par \[\boxed{\left\{\begin{array}{l}
x(t)=\dfrac{p~t^2}{2}\newline y(t)= p~t \end{array}\right. :t \in \mathbb{R}}\]
Soit \(\mathscr R\left(O,\overrightarrow{i}, \overrightarrow{j}\right)\) le repère construit dans la proposition précédente. Dans ce repère une équation de \(\mathscr P\) est \(y^2-2px=0\). Soit \(M \left|\begin{matrix} x \\ y \end{matrix} \right.\) un point du plan. On a équivalence entre : \[\begin{aligned}
M\in\mathscr P &\Longleftrightarrow&y^2-2px=0\newline
&\Longleftrightarrow&\exists t\in \mathbb{R},\quad y= p~t \quad \textrm{ et} \quad x=\dfrac{p~t^2}{2}.\end{aligned}\]
Comme \(\lim_{t \rightarrow \pm \infty} {\scriptstyle y(t)\over\scriptstyle x(t)}=0\), la parabole possède deux branches paraboliques de direction asymptotique \(OX\) (c’est de là que vient l’appellation).
(Tangente à la parabole). Dans un repère \((O,\overrightarrow{i}, \overrightarrow{j})\), on considère la parabole \(\mathscr P\) de paramètre \(p>0\) et paramétrée par \(\left\{\begin{array}{l}
x(t)={\scriptstyle p~t^2\over\scriptstyle 2}\newline y(t)= p~t \end{array}\right. :t \in \mathbb{R}\).
La tangente \(\mathscr T_{M_0}\) à \(\mathscr P\) au point \(M_0\) de \(\mathscr
P\) de paramètre \(t_0\in \mathbb{R}\) a pour équation: \[\boxed{x-t_0
y+p{\scriptstyle t_0^2\over\scriptstyle 2}=0}\]
La tangente \(\mathscr T_{M_0}\) à \(\mathscr P\) au point \(M_0(x_0,y_0)\) a pour équation \[y~y_0 = p (x+x_0)\]
Soit \(\mathscr T_0\) la tangente à \(\mathscr P\) au point de paramètre \(t_0\). Un vecteur directeur à cette tangente a pour coordonnées \(\left(pt_0,p\right)\). Le vecteur de coordonnées \(\left(t_0,1\right)\) dirige donc \(\mathscr T_0\). Une équation cartésienne de \(\mathscr T_0\) est donc \[\left|
\begin{array}{cc}
t_0&x-x\left(t_0\right)\newline
1 & y - y\left(t_0\right)
\end{array}
\right| =0 .\] soit \(t_0 \left(y-pt_0\right) - \left(x-{\scriptstyle p~t_0^2\over\scriptstyle 2}\right)=0\) ou encore \(x-t_0 y +{\scriptstyle p~t_0^2\over\scriptstyle 2}=0\). Par ailleurs, comme \(x_0={\scriptstyle p~t_0^2\over\scriptstyle 2}\) et que \(y_0=p~t_0\), cette équation s’écrit encore \(p x - y_0 y + p x_0=0\).
Étude de l’ellipse: \(0<e<1\)
On considère dans tout ce paragraphe une ellipse \(\mathscr E\) de foyer \(F\), de directrice \(\mathscr D\) et d’excentricité \(e\) (\(0<e<1\)).
(Équation réduite de l’ellipse).
Il existe un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) dans lequel \(\mathscr
E\) a pour équation \[\boxed{\dfrac{X^2}{a^2}+\dfrac{Y^2}{b^2}=1 \quad
0<b<a}\] Cette équation est appelée équation réduite de l’ellipse\(\mathscr E\).
Réciproquement: l’équation \({\scriptstyle X^2\over\scriptstyle a^2}+{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(0<b<a\) est l’équation d’une ellipse de foyer \(\boxed{F \left|\begin{matrix} -c \\ 0 \end{matrix} \right.}\) avec \(\boxed{c=\sqrt{a^2-b^2}}\), de directrice \(\boxed{\mathscr D:~X=-{\scriptstyle a^2\over\scriptstyle c}}\) et d’excentricité \(\boxed{e={\scriptstyle c\over\scriptstyle a}}\).
D’après la proposition [rep_conique], il existe un repère orthonormal direct \(\mathscr R\left(F,\overrightarrow{i},\overrightarrow{j}\right)\) dans lequel une équation cartésienne de \(\mathscr E\) est \[x^2+y^2 = e^2 \left(x+d\right)^2
\left(\star\right)\] où \(d=d\left(F,\mathscr D\right)\). On a : \[\begin{aligned}
\left(\star\right)&\Longleftrightarrow& \left(1-e^2\right) x^2 - 2e^2 d x +y^2 - e^2 d^2=0\\
&\Longleftrightarrow& \left(1-e^2\right)\left( x^2 - \dfrac{2e^2 d}{1-e^2} x \right) +y^2 - e^2 d^2=0
\\ %\text{ On reconnat le début d'un carré}\\
&\Longleftrightarrow& \left(1-e^2\right)\left( \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 - \dfrac{e^4
d^2}{\left(1-e^2\right)^2}\right)+y^2 - e^2 d^2=0 \\%\\\text{ par factorisation}\\
&\Longleftrightarrow& \left(1-e^2\right) \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 +y^2 - e^2 d^2-
\dfrac{e^4 d^2}{1-e^2}=0 \\
&\Longleftrightarrow& \left(1-e^2\right) \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 +y^2 - \dfrac{e^2
d^2\left(1-e^2\right) +e^4 d^2 }{1-e^2}=0 \\
&\Longleftrightarrow& \left(1-e^2\right) \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 +y^2 - e^2 d^2\dfrac{
1-e^2 +e^2 }{1-e^2}=0 \\
&\Longleftrightarrow& \left(1-e^2\right) \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 +y^2 - \dfrac{ e^2
d^2
}{1-e^2}=0 \\
&\Longleftrightarrow& \left(1-e^2\right)^2 \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 + \left(1-e^2\right) y^2 -
e^2 d^2 =0 \\
&\Longleftrightarrow& \dfrac{\left(1-e^2\right)^2}{e^2d^2} \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 +
\dfrac{1-e^2}{e^2 d^2} y^2 - 1 =0 \\
&\Longleftrightarrow& \left(\dfrac{1-e^2}{ed}\right)^2 \left(x - \dfrac{e^2 d}{1-e^2}\right)^2 +
\dfrac{1-e^2}{e^2 d^2} y^2 - 1 =0 \left(\star'\right)\end{aligned}\]
Posons alors \[a=\dfrac{ed}{1-e^2},\quad
b=\dfrac{ed}{\sqrt{1-e^2}},\quad c=\dfrac{e^2 d}{1-e^2} \quad \textrm{ et} \quad\begin{cases} X=x
-
c\\ Y= y \end{cases}.\]
Ces quantités sont bien définies car \(0<e<1\). Remarquons qu’on a \(a>b>0\). Le couple \(\left(X,Y\right)\) représente les coordonnées dans un repère \(\mathscr R'\left(O,\overrightarrow{i},\overrightarrow{j}\right)\) d’un point de coordonnées \(\left(x,y\right)\) dans le repère \(\mathscr R\left(F,\overrightarrow{i},\overrightarrow{j}\right)\) où \(O\) est déduit de \(F\) par une translation de vecteur \(\overrightarrow{u} \left|\begin{matrix} c \\ 0 \end{matrix} \right.\). Dans ce nouveau repère, \(\left(\star\right)\) s’écrit alors \[\dfrac{X^2}{a^2}+\dfrac{Y^2}{b^2}=1\] qui est bien de la forme annoncée. On a par ailleurs bien \(a^2-b^2=c^2\), \({\scriptstyle c\over\scriptstyle a}=e\) et \(d={\scriptstyle b^2\over\scriptstyle c}\). Enfin, une équation de la directrice \(\mathscr D\) dans \(\mathscr R\) étant \(x=-d\), une équation de \(\mathscr D\) dans \(\mathscr R'\) est : \(X+c=-d\), soit \(X=-d-c\). Mais \(-d-c=-\dfrac{b^2+c^2}{c}=-{\scriptstyle a^2\over\scriptstyle c}\). Une équation de \(\mathscr D\) dans \(\mathscr R'\) est donc : \(X=-{\scriptstyle a^2\over\scriptstyle c}\).
Réciproquement, soit \(\mathscr E\) une courbe d’équation \({\scriptstyle X^2\over\scriptstyle a^2}+{\scriptstyle Y^2\over\scriptstyle b^2}=1\) dans un repère \(\mathscr
R'\left(O,\overrightarrow{i},\overrightarrow{j}\right)\).avec \(a>b>0\). Posons \[c=\sqrt{a^2-b^2},\quad
e={\scriptstyle c\over\scriptstyle a} \quad \textrm{ et} \quad d={\scriptstyle b^2\over\scriptstyle c}.\] Par identification avec l’équation \(\left(\star
'\right)\), on reconnait l’ellipse de foyer \(F \left|\begin{matrix} -c \newline 0 \end{matrix} \right.\) de directrice \(\mathscr
D: X= -{\scriptstyle a^2\over\scriptstyle c}\) et d’excentricité \(e\).
Soit \((O,\overrightarrow{i}, \overrightarrow{j})\) un repère orthonormal dans lequel \(\mathscr E\) a pour équation \({\scriptstyle X^2\over\scriptstyle a^2}+{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(0<b<a\).
L’origine \(O\) est centre de symétrie de \(\mathscr E\). C’est le centre de l’ellipse.
\(OX\) et \(OY\) sont axes de symétrie de \(\mathscr E\). \(OX\) est appelé axe focal ou grand axe. \(OY\) est appelé axe non focal ou petit axe.
\(a\) est appelé demi-axe focal ou demi-grand axe. \(b\) est appelé demi-axe non focal ou demi-petit axe.
Soit \(c=\sqrt{a^2-b^2}\). \(\mathscr E\) admet deux foyers \(F\) et \(F'\) de coordonnées dans le repère \((O,\overrightarrow{i}, \overrightarrow{j})\): \(F \left|\begin{matrix} -c \\ 0 \end{matrix} \right.\) et \(F' \left|\begin{matrix} c \\ 0 \end{matrix} \right.\) de directrice associée d’équation, dans ce même repère: \(\mathscr D:~ X=-{\scriptstyle a^2\over\scriptstyle c}\) et \(\mathscr D':~ X={\scriptstyle a^2\over\scriptstyle c}\).
L’ellipse \(\mathscr E\) coupe les axes du repère \((O,\overrightarrow{i}, \overrightarrow{j})\) en quatre points \(A,~A',~B,~B'\) appelés les sommets de \(\mathscr E\) et on a: \(A \left|\begin{matrix} -a \\ 0 \end{matrix} \right.,~A' \left|\begin{matrix} a \\ 0 \end{matrix} \right.,~B \left|\begin{matrix} 0 \\ -b \end{matrix} \right.,~B' \left|\begin{matrix} 0 \newline b \end{matrix} \right.\).
(Paramétrage de l’ellipse). On peut paramétrer l’ellipse d’équation \({\scriptstyle X^2\over\scriptstyle a^2}+{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(0<b<a\) dans un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) par \[\boxed{\left\{\begin{array}{l} x(t)=a \cos t \newline y(t)= b \sin t
\end{array}\right. :t \in [-\pi,\pi]}\]
Soit \(\mathscr R\left(O,\overrightarrow{i}, \overrightarrow{j}\right)\) le repère construit dans la proposition précédente. Dans ce repère une équation de \(\mathscr E\) est \({\scriptstyle X^2\over\scriptstyle a^2}+{\scriptstyle Y^2\over\scriptstyle b^2}=1\). Soit \(M \left|\begin{matrix} X \\ Y \end{matrix} \right.\) un point du plan. On a équivalence entre : \[\begin{aligned}
M\in\mathscr E &\Longleftrightarrow&\dfrac{X^2}{a^2}+\dfrac{Y^2}{b^2}=1\newline
&\Longleftrightarrow&\exists t\in [-\pi,\pi],\quad X= a \cos t \quad \textrm{ et} \quad Y=b \sin t\end{aligned}\]
L’ellipse ne possède pas de branche infinie.
Les-mathematiques.net
(Pour construire une ellipse).
On trace ses axes focaux et demi-focaux.
On place le centre \(O\) de l’ellipse puis ses quatre sommets \(A,A',B,B'\).
On mesure au compas la longueur \(OA\) et on place le compas en \(B\).
On trace les deux arcs intersectant l’axe focal. On obtient ainsi les points \(F\) et \(F'\).
(Affinité orthogonale). Soient \((O,\overrightarrow{i},\overrightarrow{j})\) un repère orthonormal. L’affinité orthogonale de base \((O,\overrightarrow{i})\) et de rapport \(k\in \mathbb{R}\) est l’application du plan dans lui-même qui au point \(M\) de coordonnées \((x,y)\) associe le point \(M'\) de coordonnées \((x,ky)\).
(Cercle principal d’une ellipse). L’ellipse \(\mathscr E\) d’équation \({\scriptstyle X^2\over\scriptstyle a^2}+{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(0<b<a\) dans un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) est l’image du cercle \(\mathscr C\) d’équation cartésienne \(X^2+Y^2=a^2\) par l’affinité orthogonale de base \((O,\overrightarrow{i})\) et de rapport \(k={\scriptstyle b\over\scriptstyle a}\). Le cercle \(\mathscr C\) est appelé cercle principal de l’ellipse \(\mathscr E\).
Soit \(M\) un point de \(\mathscr C\). Il existe \(t\in\left[-\pi,\pi\right]\) tel que les coordonnées de \(M\) soient \(\left(a\cos t,a\sin t \right)\). Soit \(T\) l’affinité orthogonale en question. On a \(T\left(M\right) \left|\begin{matrix} a\cos t \newline b\sin t \end{matrix} \right.\). Donc \(T\left(M\right)\in \mathscr
E\). Réciproquement, tout point de \(\mathscr E\) est image d’un point de \(\mathscr
C\) par \(T\).
(Équation de la tangente à une ellipse). Dans un repère \((O,\overrightarrow{i}, \overrightarrow{j})\), on considère l’ellipse \(\mathscr E\) de demi-grand axe \(a\) et de demi-petit axe \(b\) (\(0<b<a\)) et paramétrée par \(\left\{\begin{array}{l} x(t)=a \cos t \newline y(t)= b \sin t \end{array}\right. :t
\in [-\pi,\pi]\).
La tangente \(\mathscr T_{M_0}\) à \(\mathscr E\) au point \(M_0\) de \(\mathscr
E\) de paramètre \(t_0\in \mathbb{R}\) a pour équation: \[b ~x~ \cos t_0 + a ~y ~\sin t_0
-ab=0\]
La tangente \(\mathscr T_{M_0}\) à \(\mathscr E\) au point \(M_0(x_0,y_0)\) a pour équation \[\dfrac{x~x_0}{a^2} +\dfrac{y ~ y_0}{b^2} -1= 0\]
Un vecteur tangent à l’ellipse \(\mathscr E\) en le point \(M\) de paramètre \(t\) est celui de coordonnées \(\left(-a\sin t,b \cos t \right)\). Une équation de la tangente \(\mathscr T_M\) à \(\mathscr E\) en \(M\) est donc : \[\left|
\begin{array}{cc}
-a\sin t&x-a\cos t\newline
b \cos t& y - b\sin t
\end{array}
\right| =0\] ce qui donne : \(b ~x~ \cos t + a ~y ~\sin t -ab=0\).
Si \(\left(x_0,y_0\right)\) sont les coordonnées de \(M_0\), cette équation devient :\({\scriptstyle x~x_0\over\scriptstyle a^2} +{\scriptstyle y ~ y_0\over\scriptstyle b^2} -1= 0\).
Les-mathematiques.net
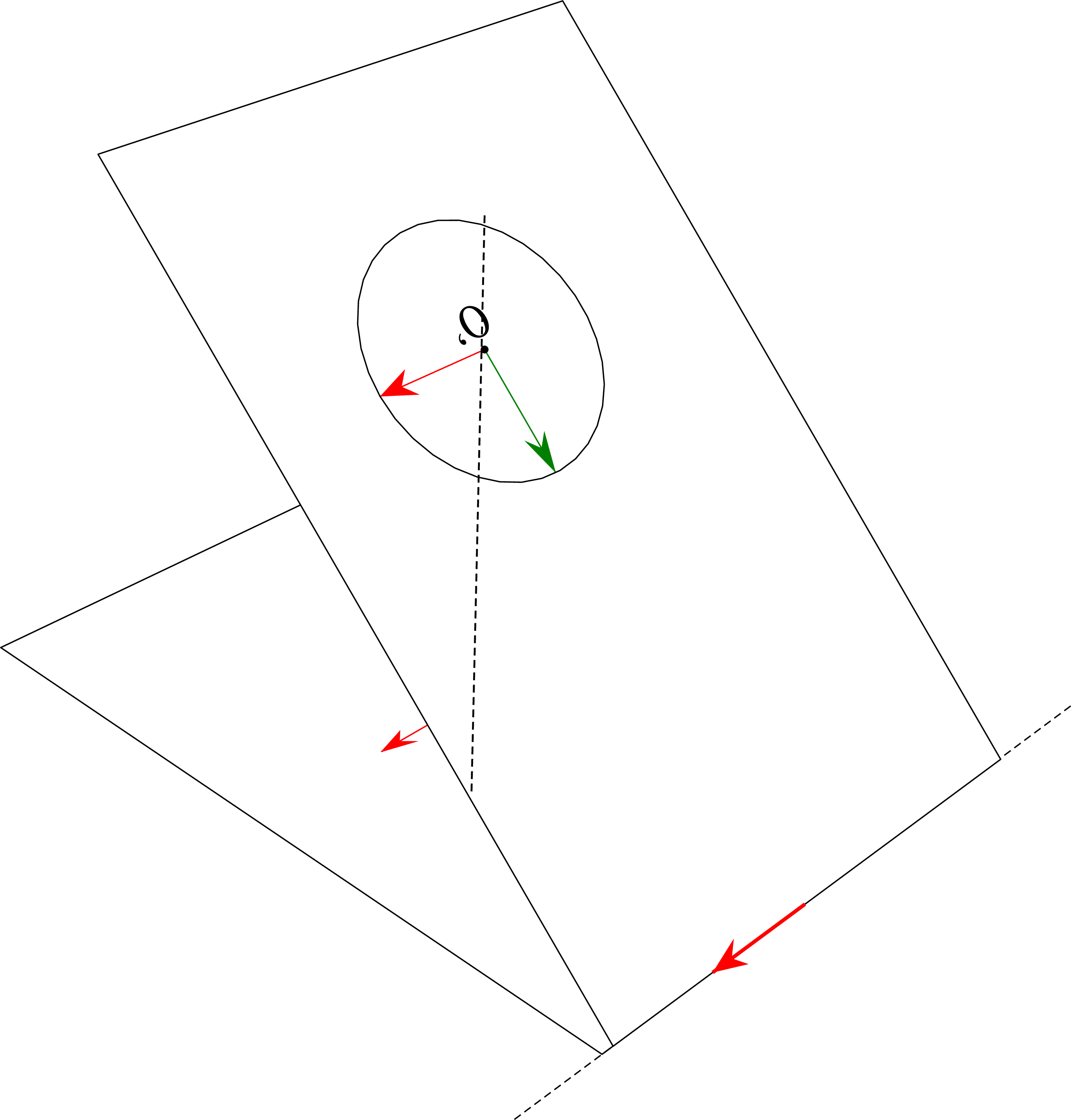
(L’image d’un cercle dans l’espace par une projection orthogonale est une ellipse). L’image d’un cercle \(\mathscr C\) de l’espace par une projection orthogonale sur un plan \(\mathscr P\) non perpendiculaire au plan contenant \(\mathscr C\) est une ellipse de \(\mathscr P\).
Nommons \(\mathscr P'\) le plan contenant le cercle \(\mathscr C\), \(r\) le rayon de \(\mathscr C\), \(O'\) son centre et \(O\) le projeté orthogonale de \(O'\) sur le plan \(\mathscr P\) .
Si les plans \(\mathscr P\) et \(\mathscr P'\) sont parallèles alors l’image de \(\mathscr C\) par la projection orthogonale sur \(\mathscr P\) est le cercle de même rayon et de centre \(O\).
On suppose que \(\mathscr
P'\) est non parallèle à \(\mathscr P\). On note alors \(\mathscr D\) la droite formée par leur intersection et \(\alpha\in\left]0,\pi/2\right[\) l’angle non orienté entre les plans \(\mathscr P\) et \(\mathscr P'\). Soit \(\overrightarrow{i}\) un vecteur unitaire dirigeant \(\mathscr D\). Soit \(\overrightarrow{j}\) un vecteur de \(\mathscr P\) en sorte que \(\mathscr R\left(O,\overrightarrow{i},\overrightarrow{j}\right)\) soit un repère orthonormal de \(\mathscr P\). De la même façon, on considère un vecteur \(\overrightarrow{j}'\) en sorte que \(\mathscr R'\left(O',\overrightarrow{i}',\overrightarrow{j}'\right)\) soit un repère orthonormal de \(\mathscr P'\). \(\theta\in\mathbb{R}\). Par la projection orthogonale sur \(\mathscr P\), le point \(M'\in\mathscr P'\) de coordonnées \(\left(x,y\right)\) dans \(\mathscr R'\) se transforme en le point \(M \in\mathscr P\) de coordonnées \(\left(x,y\cos \alpha\right)\) dans \(\mathscr
R\).
Si \(M'\) est élément de \(\mathscr C\) alors il existe \(\theta\in\mathbb{R}\) tel que \(x=r\cos \theta\) et \(y=r\sin \theta\) et les coordonnées de \(M'\) sont alors \(\left(r\cos \theta,r\sin\theta\cos \alpha\right)\). Donc \(M'\) est élément de l’ellipse de centre \(O\), de demi grand axe \(r\) et de demi petit axe \(R\cos \alpha\). Réciproquement, on vérifie que si \(M\left(r\cos \theta,r\sin\theta\cos \alpha\right)\) est élément de cette ellipse alors c’est le projeté orthogonal sur \(\mathscr P\) du point \(M'\left(r\cos \theta,r\sin\theta\right)\) de \(\mathscr P'\).
Étude de l’hyperbole: \(1<e\)
On considère dans tout ce paragraphe une hyperbole \(\mathscr H\) de foyer \(F\), de directrice \(\mathscr D\) et d’excentricité \(e\) (\(e>1\)).
(Équation réduite de l’hyperbole).
Il existe un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) dans lequel \(\mathscr
H\) a pour équation \[\boxed{\dfrac{X^2}{a^2}-\dfrac{Y^2}{b^2}=1 \quad a>0,
~
b>0}\] Cette équation est appelée équation réduite de l’hyperbole\(\mathscr H\).
Réciproquement: l’équation \({\scriptstyle X^2\over\scriptstyle a^2}-{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(a>0, ~ b>0\) est l’équation d’une hyperbole de foyer \(\boxed{F \left|\begin{matrix} c \newline 0 \end{matrix} \right.}\) avec \(\boxed{c=\sqrt{a^2+b^2}}\), de directrice \(\boxed{\mathscr D:~X={\scriptstyle a^2\over\scriptstyle c}}\) et d’excentricité \(\boxed{e={\scriptstyle c\over\scriptstyle a}}\).
D’après la proposition [rep_conique], il existe un repère orthonormal direct \(\mathscr R\left(F,\overrightarrow{i},\overrightarrow{j}\right)\) dans lequel une équation cartésienne de \(\mathscr H\) est \[x^2+y^2 = e^2 \left(x+d\right)^2
\left(\star\right)\] où \(d=d\left(F,\mathscr D\right)\). On a : \[\begin{aligned}
\left(\star\right)&\Longleftrightarrow& \left(1-e^2\right) x^2 - 2e^2 d x +y^2 - e^2 d^2=0\\
&\Longleftrightarrow& \left(e^2-1\right) x^2 + 2e^2 d x -y^2 + e^2 d^2=0\\
&\Longleftrightarrow& \left(e^2-1\right)\left( x^2 + \dfrac{2e^2 d}{e^2-1} x \right) -y^2 + e^2 d^2=0
\\%\text{ On reconnaît le début d'un carré}\\
&\Longleftrightarrow& \left(e^2-1\right)\left( \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 - \dfrac{e^4
d^2}{\left(e^2-1\right)^2}\right)-y^2 + e^2 d^2=0 \\% \text{ par factorisation}\\
&\Longleftrightarrow& \left(e^2-1\right) \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 -y^2 + e^2 d^2-
\dfrac{e^4 d^2}{e^2-1}=0 \\
&\Longleftrightarrow& \left(e^2-1\right) \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 -y^2 + \dfrac{e^2
d^2\left(e^2-1\right) -e^4 d^2 }{e^2-1}=0 \\
&\Longleftrightarrow& \left(e^2-1\right) \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 -y^2 + e^2 d^2\dfrac{
e^2-1 -e^2 }{e^2-1}=0 \\
&\Longleftrightarrow& \left(e^2-1\right) \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 -y^2 - \dfrac{ e^2
d^2
}{e^2-1}=0 \\
&\Longleftrightarrow& \left(e^2-1\right)^2 \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 - \left(e^2-1\right) y^2 -
e^2 d^2 =0 \\
&\Longleftrightarrow& \dfrac{\left(e^2-1\right)^2}{e^2d^2} \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 -
\dfrac{e^2-1}{e^2 d^2} y^2 - 1 =0 \\
&\Longleftrightarrow& \left(\dfrac{e^2-1}{ed}\right)^2 \left(x + \dfrac{e^2 d}{e^2-1}\right)^2 -
\dfrac{e^2-1}{e^2 d^2} y^2 - 1 =0 \left(\star'\right)\end{aligned}\] Posons alors \[a=\dfrac{ed}{e^2-1},\quad
b=\dfrac{ed}{\sqrt{e^2-1}},\quad c=\dfrac{e^2 d}{e^2-1} \quad \textrm{ et} \quad\begin{cases} X=x
+
c\\ Y= y \end{cases}.\]
Ces quantités sont bien définies car \(e>1\). Remarquons que \(a>0\) et \(b>0\). \(\left(X,Y\right)\) sont les coordonnées dans un repère \(\mathscr R'\left(O,\overrightarrow{i},\overrightarrow{j}\right)\) d’un point de coordonnées \(\left(x,y\right)\) dans le repère \(\mathscr R\left(F,\overrightarrow{i},\overrightarrow{j}\right)\) où \(O\) est déduit de \(F\) par une translation de vecteur \(\overrightarrow{u} \left|\begin{matrix} -c \\ 0 \end{matrix} \right.\). Dans ce nouveau repère, \(\left(\star\right)\) s’écrit alors \[\dfrac{X^2}{a^2}-\dfrac{Y^2}{b^2}=1\] qui est bien de la forme annoncée. On a par ailleurs bien \(a^2+b^2=c^2\), \({\scriptstyle c\over\scriptstyle a}=e\) et \(d={\scriptstyle b^2\over\scriptstyle c}\). Dans \(\mathscr R'\), on a \(F \left|\begin{matrix} c \\ 0 \end{matrix} \right.\). Enfin, une équation de la directrice \(\mathscr D\) dans \(\mathscr R\) étant \(x=-d\), une équation de \(\mathscr D\) dans \(\mathscr R'\) est \(X-c=-d\), soit \(X=c-d\). Mais \(c-d={\scriptstyle c^2-b^2\over\scriptstyle c}={\scriptstyle a^2\over\scriptstyle c}\). Une équation de \(\mathscr
D\) dans \(\mathscr R'\) est donc \(X={\scriptstyle a^2\over\scriptstyle c}\).
Réciproquement, soit \(\mathscr H\) une courbe d’équation \({\scriptstyle X^2\over\scriptstyle a^2}-{\scriptstyle Y^2\over\scriptstyle b^2}=1\) dans un repère \(\mathscr
R'\left(O,\overrightarrow{i},\overrightarrow{j}\right)\) avec \(a>0\) et \(b>0\). Posons \[c=\sqrt{a^2+b^2},\quad
e={\scriptstyle c\over\scriptstyle a} \quad \textrm{ et} \quad d={\scriptstyle b^2\over\scriptstyle c}.\] Par identification avec l’équation \(\left(\star
'\right)\), on reconnait l’hyperbole de foyer \(F \left|\begin{matrix} c \newline 0 \end{matrix} \right.\) de directrice \(\mathscr D: X= {\scriptstyle a^2\over\scriptstyle c}\) et d’excentricité \(e\).
Soit \((O,\overrightarrow{i}, \overrightarrow{j})\) un repère orthonormal dans lequel l’hyperbole \(\mathscr H\) a pour équation \({\scriptstyle X^2\over\scriptstyle a^2}-{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(a>0, ~ b>0\).
L’origine \(O\) est centre de symétrie de \(\mathscr H\). C’est le centre de l’hyperbole.
\(OX\) et \(OY\) sont axes de symétrie de \(\mathscr H\). \(OX\) est appelé axe focal ou grand axe. \(OY\) est appelé axe non focal ou axe non transverse.
\(a\) est appelé demi-axe focal ou demi-grand axe. \(b\) est appelé demi-axe non focal ou demi-petit axe.
Soit \(c=\sqrt{a^2+b^2}\). \(\mathscr H\) admet deux foyers \(F\) et \(F'\) de coordonnées dans le repère \((O,\overrightarrow{i}, \overrightarrow{j})\): \(F \left|\begin{matrix} c \\ 0 \end{matrix} \right.\) et \(F' \left|\begin{matrix} -c \\ 0 \end{matrix} \right.\) de directrice associée d’équation, dans ce même repère,: \(\mathscr D:~ X={\scriptstyle a^2\over\scriptstyle c}\) et \(\mathscr D':~ X=-{\scriptstyle a^2\over\scriptstyle c}\).
L’hyperbole \(\mathscr H\) coupe le grand axe en deux points \(A\) et \(A'\) appelés les sommets de \(\mathscr
H\)· On a \(A \left|\begin{matrix} a \\ 0 \end{matrix} \right.\) et \(A' \left|\begin{matrix} -a \newline 0 \end{matrix} \right.\)
(Paramétrage de l’hyperbole). On peut paramétrer l’hyperbole d’équation \({\scriptstyle X^2\over\scriptstyle a^2}-{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(a>0, ~ b>0\) dans un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\) par \[\boxed{\left\{\begin{array}{l} x(t)=\varepsilon a \mathop{\mathrm{ch}}t \newline y(t)= b
\mathop{\mathrm{sh}}t \end{array}\right. :t \in \mathbb{R}, ~ \varepsilon = \pm 1}\]
Soit \(\mathscr R\left(O,\overrightarrow{i}, \overrightarrow{j}\right)\) le repère construit dans la proposition précédente. Dans ce repère une équation de \(\mathscr H\) est \({\scriptstyle X^2\over\scriptstyle a^2}-{\scriptstyle Y^2\over\scriptstyle b^2}=1\). Soit \(M \left|\begin{matrix} X \\ Y \end{matrix} \right.\) un point du plan. On a équivalence entre : \[\begin{aligned}
M\in\mathscr H &\Longleftrightarrow&\dfrac{X^2}{a^2}-\dfrac{Y^2}{b^2}=1\newline
&\Longleftrightarrow&\exists t\in \mathbb{R},\quad Y=b \mathop{\mathrm{sh}}t \quad \textrm{ et} \quad X= \pm a \mathop{\mathrm{ch}}t\end{aligned}\]
Remarquons que l’hyperbole possède des branches infinies.
(Asymptotes à l’hyperbole). Soit \(\mathscr H\) l’hyperbole d’équation \({\scriptstyle X^2\over\scriptstyle a^2}-{\scriptstyle Y^2\over\scriptstyle b^2}=1\) avec \(a>0, ~ b>0\) dans un repère orthonormal \((O,\overrightarrow{i}, \overrightarrow{j})\). \(\mathscr H\) admet deux asymptotes: \(\boxed{\delta : ~ b~X - a ~ Y=0}\) et \(\boxed{\delta' : ~ b~X + a ~ Y=0}\).
Nous allons nous limiter à la branche correspondant à \(\varepsilon=1\) et montrer que cette branche admet les deux asymptotes indiquées. Par symétrie d’axe \(\left(Oy\right)\), on en déduira que la branche de l’hyperbole correspondant à \(\varepsilon=-1\) admet aussi ces deux droites comme asymptotes. Commençons par l’étude de la branche infinie quand \(t\) tend vers \(+\infty\). On a : \[\dfrac{y\left(t\right)}{x\left(t\right)} = \dfrac{b\mathop{\mathrm{sh}}t}{a\mathop{\mathrm{ch}}t} = \dfrac{b}{a} \operatorname{th} t
\xrightarrow[t\rightarrow +\infty]{} \dfrac{b}{a}\] De plus : \[y\left(t\right)- \dfrac{b}{a} x\left(t\right) = b\left(\mathop{\mathrm{sh}}t - \mathop{\mathrm{ch}}t\right) = -be^{-t}
\xrightarrow[t\rightarrow +\infty]{} 0\] Par conséquent, la droite d’équation \(y={\scriptstyle b\over\scriptstyle a}x\), soit \(bx-ay=0\) est asymptote à l’hyperbole. De plus : \(y\left(t\right)- {\scriptstyle b\over\scriptstyle a} x\left(t\right)=-be^{-t}<0\). La courbe est donc en dessous de l’asymptote. On fait de même pour l’asymptote à la branche infinie quand \(t\) tend vers \(-\infty\). On peut aussi utiliser la symétrie de l’hyperbole par rapport à l’axe \(\left(Ox\right)\) et déduire ainsi la seconde asymptote de la première.
Les-mathematiques.net
(Pour construire une hyperbole).
On trace ses axes focal et demi-focal.
On place le centre \(O\) de l’hyperbole puis ses deux sommets \(A\) et \(A'\).
On trace le cercle de centre \(O\) et de rayon \(a\) .
On trace les asymptotes.
Pour une de ces deux asymptotes, on considère son intersection avec le cercle. Elle est formée de deux points \(P\) et \(P'\).
On trace les perpendiculaires à l’asymptote passant par chacun de ces deux points.
L’intersection de chacune de ces deux perpendiculaires avec l’axe focal est constituée des deux foyers de l’hyperbole.
Les directrices de l’hyperbole sont les droites perpendiculaires à l’axe focal et passant par \(P\) et \(P'\).
Définition bifocale de l’ellipse et de l’hyperbole
(Définition bifocale de l’ellipse et de l’hyperbole). Soient \(a\) et \(c\) deux réels strictement positifs, \(F\) et \(F'\) deux points du plan tels que \(\left\|\overrightarrow{FF'}\right\|=2c\).
Si \(a>c\), l’ensemble des points du plan tels que \[\boxed{\left\|\overrightarrow{MF}\right\|+ \left\|\overrightarrow{MF'}\right\| = 2a}\] est l’ellipse de foyers \(F\) et \(F'\) et de demi-grand axe \(a\)
Si \(a<c\), l’ensemble des points du plan tels que \[\boxed{\left|
\left\|\overrightarrow{MF}\right\| - \left\|\overrightarrow{MF'}\right\| \right| = 2a}\] est l’hyperbole de foyers \(F\) et \(F'\) et de demi-axe focal \(a\).
Introduisons le point \(O\) milieu de \(\left[F,F'\right]\) et \(\overrightarrow{i}=\overrightarrow{OF}/\left\|\overrightarrow{OF}\right\|\). Soit \(\overrightarrow{j}\) un vecteur unitaire directement orthogonal à \(\overrightarrow{i}\). On forme ainsi un repère orthonormal direct \(\left(O,\overrightarrow{i},\overrightarrow{j}\right)\). Dans ce repère, on a \(F\left(c,0\right)\), \(F'\left(-c,0\right)\). Soit \(M\left(x,y\right)\) un point de plan. On calcule \(MF^2= \left(x-c\right)^2+y^2\) et \(MF'^2= \left(x+c\right)^2+y^2\) et il s’ensuit que \[MF^2.MF'^2=\left(\left(x-c\right)^2+y^2\right)\left(\left(x+c\right)^2+y^2\right)=\left(x^2+y^2+c^2-2cx\right)\left(
x^2+y^2+c^2+2cx\right)=\left(x^2+y^2+c^2\right)^2-4c^2x^2\] et que \[MF^2+MF'^2=\left(x-c\right)^2+y^2+\left(x+c\right)^2+y^2=2\left(x^2+y^2+c^2\right).\]
On a alors les équivalences : \[\begin{aligned}
& &MF+ MF' = 2a\\
&\Longleftrightarrow& MF^2+MF'^2+2MF.MF'=4a^2\\
&\Longleftrightarrow&2MF.MF'=4a^2-\left(MF^2+MF'^2\right)\\
&\Longleftrightarrow&4MF^2 .MF'^2=\left(4a^2-\left(MF^2+MF'^2\right)\right)^2\\
&\Longleftrightarrow&\left(x^2+y^2+c^2\right)^2-4c^2x^2=\left(2a^2 - \left(x^2 + y^2+c^2\right)\right)^2\\
&\Longleftrightarrow&\left(a^2-c^2\right)x^2+a^2 y^2=a^2\left(a^2-c^2\right)\\
&\Longleftrightarrow&b^2x^2+a^2 y^2=a^2b^2\\
&\Longleftrightarrow&\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\end{aligned}\] où \(b^2=a^2-c^2\) est bien défini car \(a>c\). Donc on a \(MF+ MF' = 2a\) si et seulement si \(M\) est élément de l’ellipse de centre \(O\), de demi-grand axe \(a\) et de demi-petit axe \(b\).
On a les équivalences : \[\begin{aligned}
& &\left|MF- MF'\right| = 2a\\
&\Longleftrightarrow& MF^2+MF'^2-2MF.MF'=4a^2\\
&\Longleftrightarrow&2MF.MF'=\left(MF^2+MF'^2\right)-4a^2\\
&\Longleftrightarrow&4MF^2 .MF'^2=\left(\left(MF^2+MF'^2\right)-4a^2\right)^2\\
&\Longleftrightarrow&\left(x^2+y^2+c^2\right)^2-4c^2x^2=\left( \left(x^2 + y^2+c^2\right)-2a^2 \right)^2\\
&\Longleftrightarrow&\left(a^2-c^2\right)x^2+a^2 y^2=a^2\left(a^2-c^2\right)\\
&\Longleftrightarrow&\left(c^2-a^2\right)x^2-a^2 y^2=a^2\left(c^2-a^2\right)\\
&\Longleftrightarrow&b^2x^2-a^2 y^2=a^2b^2\newline
&\Longleftrightarrow&\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\end{aligned}\] où \(b^2=c^2-a^2\) est bien défini car \(a<c\). Donc on a \(\left|MF- MF'\right| = 2a\) si et seulement si \(M\) est élément de l’hyperbole de centre \(O\), de demi-grand axe \(a\) et de demi-petit axe \(b\).
Application: Comment dessiner une ellipse avec un crayon et une ficelle.
Courbes algébriques dans le plan
Le plan est rapporté dans tout ce paragraphe à un repère orthonormal direct \(\mathscr R\left(O,\overrightarrow{i},\overrightarrow{j}\right)\). On s’intéresse ici à l’ensemble \(\mathscr C\) des points du plan dont une équation cartésienne est : \[P\left(x,y\right)=a x^2 + 2 b xy +c y^2 + dx+ey+f=0\] où \(\left(a,b,c,d,e,f\right)\in\mathbb{R}^6\) et où les réels \(a\), \(b\) et \(c\) ne sont pas tous nuls (sinon \(\mathscr C\) est une droite affine du plan).
On appelle discriminant de la courbe du second degré : \[\mathscr C~: a x^2 + 2 b xy +c y^2 + dx+ey+f=0\] le réel, noté \(\Delta\) et donné par : \(\Delta=ac-b^2\).
(Élimination du terme en \(xy\)). Il existe une rotation de centre \(O\) et d’angle \(\theta\in\mathbb{R}\) telle que dans le repère \(\mathscr R'\left(O,\overrightarrow{i}',\overrightarrow{j}'\right)\) déduit du repère \(\mathscr R\) par cette rotation, l’équation de \(\mathscr C\) devient : \[\mathscr C~:AX^2+CY^2+DX+EY+F =0.\] De plus \(\Delta=ac-b^2=AC\) (et \(F=f\)).
On utilise les formules de changement de repère de la proposition [prop:20100501130201] page [prop:20100501130201] : \[\begin{cases}
x&=\cos \theta X-\sin \theta Y\\
y&=\sin \theta X+\cos \theta Y
\end{cases}\] où \(\theta\) est un réel à déterminer. On a : \[\begin{aligned}
& & a x^2 + 2 b xy +c y^2 + dx+ey+f=0\\
&\Longleftrightarrow&
\left(a\cos^2\theta + c\sin^2 \theta +2b\sin\theta\cos\theta\right)X^2+
\left(a\sin^2\theta + c\cos^2 \theta -2b\sin\theta\cos\theta\right)Y^2+\\
& &\quad\quad\quad\quad\left(2\left(c-a\right)\sin\theta\cos\theta +2
b\left(\cos^2\theta-\sin^2\theta\right)\right)XY
+ \left(d\cos\theta + e\sin \theta\right)X + \left(e\cos\theta -d\sin\theta\right)Y+f=0\newline\end{aligned}\]
On cherche \(\theta\) en sorte que \(2\left(c-a\right)\sin\theta\cos\theta +
2b\left(\cos^2\theta-\sin^2\theta\right)=0\) ce qui s’écrit aussi \(\left(c-a\right)\sin2\theta +
2b\cos 2\theta=0\).
Si \(a=c\) alors on peut prendre \(\theta=\pi/4\).
Si \(a\neq c\) alors on peut prendre \(\theta={\scriptstyle 1\over\scriptstyle 2}\operatorname{arctan} \left({\scriptstyle 2b\over\scriptstyle a-c}\right)\).
Dans le nouveau repère, l’équation de \(\mathscr C\) est bien de la forme annoncée avec \(A=a\cos^2\theta + c\sin^2 \theta
+2b\sin\theta\cos\theta\) , \(C=a\sin^2\theta + c\cos^2 \theta
-2b\sin\theta\cos\theta\), \(D=d\cos\theta + e\sin \theta\), \(E=e\cos\theta
-d\sin\theta\) et \(F=f\).
On remarque que \(A+C=a+c\), que \(A-C=\left(a -c\right)\cos 2\theta + 2b\sin 2\theta\) et que \(AC=1/4
\left(\left(A+C\right)^2-\left(A-C\right)^2\right)\).
Si \(a=0\) et donc \(\theta=\pi/4\), on vérifie facilement que \(ac-b^2=AC\). Sinon, si \(\theta =
{\scriptstyle 1\over\scriptstyle 2}\operatorname{arctan} \left({\scriptstyle 2b\over\scriptstyle a-c}\right)\), alors \(\tan 2\theta=2b/(a-c)\) et \[\cos^2 2\theta=\dfrac{1}{1+\tan^2
2\theta}=\dfrac{\left(a-c\right)^2}{\left(a-c\right)^2+4b^2}\] donc \[A-C=\left(a-c\right)\cos
2\theta\left(1+\dfrac{2b}{a-c}\tan 2\theta\right)=\left(a-c\right)\cos
2\theta\left(1+\tan^2 \theta\right)=\dfrac{a-c}{\cos 2\theta}\] et \(\left(A-C\right)^2={\left(a-c\right)^2+4b^2}\).
Donc \[AC= \dfrac{1}{4}
\left(\left(A+C\right)^2-\left(A-C\right)^2\right)= \dfrac{1}{4} \left( \left(a+c\right)^2-\left(a-c\right)^2\right)-b^2=ac-b^2.\]
(Élimination des termes linéaires). Si \(\Delta \neq 0\) alors il existe un repère orthonormal \(\mathscr R''
\left(\Omega,\overrightarrow{i}',\overrightarrow{j}'\right)\) déduit de \(\mathscr R'\) par une translation dans lequel une équation de \(\mathscr C\) est : \[A u^2 + C v^2 = F'\] où \(F'\in\mathbb{R}\).
Le repère \(\mathscr R''\) est déduit du repère \(\mathscr R'\) par une translation de vecteur \(\left(\alpha,\beta\right)\in\mathbb{R}^2\) à déterminer. On a donc les formules de changement de repère : \[\begin{cases}X&=u+\alpha\\Y&=v+\beta \end{cases}\] et \[\begin{aligned}
& & AX^2+CY^2+DX+EY+F =0\\
&\Longleftrightarrow& Au^2+Cv^2 + \left(2A\alpha +D\right)u+\left(2C\beta +E\right)v+A\alpha^2+C\beta^2+D
\alpha+E\beta+F=0\end{aligned}\]
On cherche \(\left(\alpha,\beta\right)\) en sorte que \[\begin{cases}2A\alpha+D&=0\newline2C\beta+E&=0 \end{cases}.\] Comme \(\Delta=AC\neq
0\), ce système admet comme solutions \(\alpha=-D/(2A)\) et \(\beta=-E/(2C)\). On en déduit \(F''\) en remplaçant \(\alpha\) et \(\beta\) par ces valeurs dans \(A\alpha^2+C\beta^2+D\alpha+E\beta+F\). Dans ce nouveau repère, l’équation de \(\mathscr C\) est bien de la forme annoncée.
On en déduit le théorème de classification des courbes du second degré, dû à Descartes (voir [René_Descartes] page [René_Descartes]).
(Classification des courbes du second degré). On considère une courbe du second degré d’équation : \[\mathscr C:\quad ax^2+2 b xy +c y^2 + dx+ey+f=0\] dans un repère orthonormal. On note \(\Delta=ac-b^2\) son discriminant.
Si \(\Delta>0\), la courbe \(\mathscr C\) est une ellipse, un point ou l’ensemble vide.
Si \(\Delta<0\), la courbe \(\mathscr C\) est une hyperbole ou la réunion de deux droites sécantes.
Si \(\Delta=0\), la courbe \(\mathscr C\) est une parabole, une droite, la réunion de deux droites parallèles ou l’ensemble vide.
D’après le lemme [lemme_elimination_XY], on peut trouver un repère dans lequel une équation de \(\mathscr C\) est \(AX^2+CY^2+DX+EY+F =0\) où \(A,C,D,E,F\in\mathbb{R}\) et où \(\Delta=ac-b^2=AC\).
Si \(\Delta=0\) alors \(A=0\) ou \(C=0\).
Si \(A=0\) et \(C\neq 0\) alors \(\mathscr C~: C Y^2 +DX+EY+F=0\) qui s’écrit aussi \(\mathscr C~: C\left(Y+E/(2C)\right)^2+DX+F-E^2/(4C)=0\).
Si \(D\neq 0\) alors en posant \(Y'=Y+{\scriptstyle E\over\scriptstyle 2C}\) et \(X'=-{\scriptstyle 1\over\scriptstyle 2C}\left(X+ {\scriptstyle F\over\scriptstyle D}-{\scriptstyle E^2\over\scriptstyle 4CD}\right)\) on obtient : \(\mathscr
C~: Y'^2-2DX'=0\) et on reconnaît une parabole.
Si \(D=0\), alors en effectuant le même travail, on montre qu’une équation de \(\mathscr C\) dans un repère convenablement choisi est de la forme \(Y'^2+F'=0\). Si \(F'>0\), \(\mathscr C\) est l’ensemble vide, si \(F'=0\), \(\mathscr
C\) est la droite d’équation \(Y'=0\) et enfin si \(F'<0\), \(\mathscr C\) est la réunion des droites parallèles d’équations \(Y'=\sqrt{-F'}\) et \(Y'= - \sqrt{-
F'}\).
Si \(A\neq 0\) et \(C= 0\) alors \(\mathscr C~: AX^2 +DX+EY+F=0\), on retrouve les mêmes résultats que dans le cas précédent .
Si \(A= 0\) et \(C= 0\) alors la courbe n’est plus du second degré.
Si \(\Delta\neq 0\), on sait d’après le lemme \(2\) que dans un bon repère, \(\mathscr C~: AX'^2+C Y'^2=F'\) avec \(A,C,F'\in\mathbb{R}\) et \(\Delta=AC\).
Si \(\Delta>0\), alors \(A\) et \(C\) sont de même signe et on peut écrire l’équation de \(\mathscr C\) sous la forme : \({\scriptstyle X'^2\over\scriptstyle A'^2}+{\scriptstyle Y'^2\over\scriptstyle C'^2}=\varepsilon\) avec \(\varepsilon=0,1\) ou \(-1\) et \(A',C'>0\). Si \(\varepsilon=0\) alors \(\mathscr C\) est réduit à un point. Si \(\varepsilon=-1\) alors \(\mathscr C\) est vide. Enfin, si \(\varepsilon=1\) alors \(\mathscr C\) est une ellipse.
Si \(\Delta<0\), alors \(A\) et \(C\) sont de signe contraire et on peut écrire l’équation de \(\mathscr C\) sous la forme : \({\scriptstyle X'^2\over\scriptstyle A'^2}-{\scriptstyle Y'^2\over\scriptstyle C'^2}=\varepsilon\) avec \(\varepsilon=0,1\) ou \(-1\) et \(A',B'>0\). Si \(\varepsilon=0\) alors l’équation s’écrit : \(\left({\scriptstyle X\over\scriptstyle A'}-{\scriptstyle Y\over\scriptstyle C'}\right)\left({\scriptstyle X\over\scriptstyle A'}+{\scriptstyle Y\over\scriptstyle C'}\right)=0\) et \(\mathscr C\) est la réunion de deux droites sécantes. Si \(\varepsilon=\pm 1\), \(\mathscr C\) est une hyperbole.
Ce théorème fournit un algorithme pour déterminer la nature d’une courbe \[\mathscr C:\quad ax^2+2 b xy +c y^2 + dx+ey+f=0\] et préciser son équation réduite.
Calculer le discriminant \(\Delta=ac-b^2\) et \(T=a+c\). Selon le signe de \(\Delta\), on peut, sans calcul, préciser le type de la courbe.
Si \(\Delta \neq 0\), par un changement du centre du repère défini par les formules : \[\begin{cases} x=X+\alpha\\ y = Y+\beta \end{cases}\] on se débarrasse des termes linéaires en \(x\) et \(y\) pour aboutir à une équation : \[ax^2+2bxy+cy^2=F\] Le centre du nouveau repère est, dans \(\mathscr R\), \(\Omega \left|\begin{matrix} \alpha \\ \beta \end{matrix} \right.\).
On sait qu’on peut, par rotation des axes, se placer dans un repère orthonormé de même centre \(\Omega\) où l’équation devient : \[Ax^2+Cy^2=F\]
On connaît la somme et le produit de \(A\) et de \(C\) : \[\begin{cases}A+C&=a+c \newlineAC&=ac-b^2\end{cases}.\] Ils sont par conséquent racines d’un trinôme du second degré.
Ayant déterminé \(A\) et \(C\), on peut écrire l’équation réduite de la conique et discuter de sa nature en fonction du signe de \(F\).
Si l’on veut avoir toutes les informations, il faut déterminer l’angle \(\theta\) de rotation choisi pour annuler le terme \(xy\).
Si \(\Delta = 0\), on peut, par rotation des axes, se placer dans un repère orthonormé de même centre où l’équation devient : \[Ax^2+By^2+Cx+Dy=F\] avec \(A=0\) ou \(B=0\). On sait alors qu’après une translation, on peut facilement identifier \(\mathscr C\).
Réduire la conique \(\mathscr C\) d’équation \(x^2+6xy+y^2+16x-9=0\).
Son discriminant vaut \(-8\) donc \(\mathscr C\) est une hyperbole ou la réunion de deux droites sécantes.
On effectue le changement de repère \(\begin{cases} x=X+\alpha\\ y =
Y+\beta \end{cases}\). On obtient : \[X^2+6 XY +Y^2+(6 \beta+2 \alpha+16)X+(2 \beta+6 \alpha)
Y-9+\beta^2+\alpha^2+16 \alpha+6 \alpha \beta=0.\] On se débarrasse des termes linéaires si \[\begin{cases}6 \beta+2 \alpha+16&=0
\\ 2 \beta+6 \alpha =0\end{cases}\] c’est-à-dire si \(\alpha=1\) et \(\beta=-3\) ce qui nous donne \(\boxed{\Omega\left(1,-3\right)}\) Dans ce nouveau repère, l’équation de \(\mathscr C\) devient : \(X^2+6XY+Y^2-1 = 0\).
On sait que par rotation des axes on peut se placer dans un repère orthonormé de même centre \(\Omega\) où l’équation devient : \[Ax^2+Cy^2=1.\] On sait que \(AC=\Delta=-8\) et que \(A+C=a+c=2\). Ils sont donc racines du polynôme \(X^2-2X-8\) et on trouve \(A=4\) et \(C=-2\) ou \(A=-2\) et \(C=4\). On obtient alors dans le nouveau repère pour \(\mathscr C\) une des deux équations \(4x^2 -2y^2=1\) ou \(-2x^2 +4y^2=1\). Ces deux équations sont obtenues dans deux repères différents, l’un étant déduit de l’autre par une rotation d’angle \(\pi/2\). On reconnaît une hyperbole de demi-axes \(1/2\) et \(\sqrt{2}/{2}\) et de centre \(\Omega\left(1,-3\right)\).
Pour mieux faire, il faut déterminer complètement la rotation. En partant de l’équation \(X^2+6XY+Y^2-1 = 0\), on effectue le changement de repère \[\begin{cases}
X&=\cos (\theta) x-\sin (\theta) y\newline
Y&=\sin (\theta) x+\cos (\theta) y
\end{cases}\] et on obtient :
\[\left(
6\sin(\theta)\cos(\theta)+\cos^2(\theta)+\sin^2(\theta)\right)x^2+
6\left(\cos^2(\theta) - \sin(\theta)^2\right)xy+
\left(\cos^2(\theta)-6\sin(\theta)\cos(\theta)+\sin^2(\theta)\right)y^2 =1\] ou encore \[\left(3\sin (2\theta) +1\right) x^2 +6\cos (2\theta) xy +\left(1-3\sin
(2\theta)\right)y^2=1.\] Pour supprimer les termes linéaires, il suffit de prendre \(\theta=\pi/4\) et on obtient dans le nouveau repère \(\mathscr C~: 4x^2 -2y^2=1\). On sait donc que \(a=1/2\), \(b=\sqrt{2}/{2}\) et \(c=\sqrt{a^2+b^2}=\sqrt 3/2\). On en déduit que \(e=c/a=\sqrt 3\). De plus, les équations des directrices dans le repère final sont \(x=\sqrt 3/6\) et \(x=-\sqrt 3/6\). Les coordonnées des foyers sont \(\left(\sqrt 3/2,0\right)\) et \(\left(-\sqrt 3/2,0\right)\). On peut alors facilement représenter \(\mathscr C\).
Les-mathematiques.net
