Lecture zen
Il se peut que \(\overrightarrow{F}'(\left(t_0\right)= 0\) et que la courbe admette en \(M\left(t_0\right)\) une tangente. Par exemple, si on considère le support de \(\overrightarrow{F}
\left(t\right)=\left(t^2,t^3\right)\) en \(t_0=0\), alors il admet en \(t_0=0\) un vecteur tangent horizontal. Pourtant ce point est stationnaire. On va étudier maintenant deux méthodes pour calculer, quand c’est possible, le vecteur tangent à une courbe en un point stationnaire.
Etude des courbes paramétrées.
Courbes paramétrées
Etude des courbes paramétrées.
On identifiera dans tout ce chapitre, le plan euclidien \(\mathscr P\) à \(\mathbb{R}^2\) à l’aide d’un repère orthonormal direct. On notera \(I\) un intervalle de \(\mathbb{R}\) non vide et non réduit à un point (ou une réunion de tels intervalles).
Nous allons apprendre ici à étudier les courbes du plan. Elles peuvent être vues comme la trajectoire d’un mobile dans le plan et il y aura de nombreuses analogies dans ce chapitre avec celui de cinématique en science physique.
r70mm
Se donner une telle courbe revient à se donner un couple de fonctions \(\left(x,y\right)\) définies sur un intervalle \(I\) de \(\mathbb{R}\) : \(x:I\rightarrow \mathbb{R}\) et \(y:I\rightarrow \mathbb{R}\). La courbe est alors le sous-ensemble du plan formé par les points \(M\left(t\right)\) de coordonnées \(\left(x\left(t\right),y\left(t\right)\right)\) quand le temps \(t\) parcourt l’intervalle \(I\).
l50mm
Même si on va utiliser les outils appris au lycée pour étudier les graphes des fonctions d’une variable réelle à valeurs dans \(\mathbb{R}\), on comprend que le problème est ici très différent. Une courbe du plan n’est en général pas le graphe d’une fonction de \(I\) dans \(\mathbb{R}\) comme on s’en convaincra en examinant le dessin ci contre. Aussi il faudra développer de nouvelles techniques. Pour une fonction \[\overrightarrow{F}: \left\{ \begin{array}{ccl} I & \longrightarrow & \mathbb{R}^2 \\ t & \longmapsto & \left(x\left(t\right),y\left(t\right)\right) \end{array} \right. ,\] il faudra définir ce qu’est une limite et une dérivée. Lors de la représentation de la courbe, il faudra comprendre que ce n’est pas le graphe de la fonction \(\overrightarrow{F}\) qui est dessiné (ce graphe est un sous-ensemble de l’espace \(\mathbb{R}^3\)) mais la projection de ce graphe sur le plan \(\left(x,y\right)\). Aussi la variable \(t\) n’est pas représentée sur le dessin. Par contre, un mobile ayant cette courbe comme trajectoire se trouve à la position \(\left(x\left(t\right),y\left(t\right)\right)\) au temps \(t\).
Les courbes paramétrées peuvent présenter des branches infinies, ce qui signifie que le mobile se déplaçant suivant cette courbe part à l’infini, ou des points stationnaires (le vecteur vitesse du mobile en ce point est nul). Il faudra être en mesure de pouvoir étudier ces deux phénomènes afin de bien représenter la courbe.
De nombreuses courbes paramétrées peuvent être étudiées avec les outils d’analyse de lycée. Par contre, afin d’étudier les branches infinies ou les points stationnaire de certaines autres, il faudra disposer d’un outil plus sophistiqué, les développements limités, qui ne sera introduit qu’au chapitre [chapitre_DL]. Aussi ce chapitre devra être lu en deux fois. Une première fois pendant la première période en sautant les parties utilisant les développements limités et une seconde fois après avoir étudié le chapitre [chapitre_DL]. Ces parties et les exercices correspondants sont indiqués dans le texte.
La voiture décrivit une élégante cardioı̈de et s’arrêta en bas des marches.Boris VIAN - L’écume des jours (1946).
Fonctions à valeurs dans \(\mathbb{R}^2\)
Définitions
(Fonction vectorielle à valeurs dans \(\mathbb{R}^2\)). Une fonction vectorielle \(\overrightarrow{F}\) à valeurs dans \(\mathbb{R}^2\) définie sur \(I\) est donnée par un couple \((x,y)\) de fonctions réelles définies sur \(I\). Les fonctions \(x: I \longrightarrow R\) et \(y: I \longrightarrow R\) s’appellent les composantes de \(\overrightarrow{F}\) ou les applications coordonnées de \(\overrightarrow{F}\) et: \[\overrightarrow{F}: \left\{ \begin{array}{ccl} I & \longrightarrow & \mathbb{R}^2 \newline t & \longmapsto & (x(t),y(t)) \end{array} \right. .\]
(Limite en un point d’une application vectorielle). Soient \(\overrightarrow{l}=(l_1,l_2)\) un vecteur de \(\mathbb{R}^2\), \(t_0\in I\) et \(\overrightarrow{F}\) une application vectorielle définie sur \(I\). On dit que \(\overrightarrow{F}\left(t\right)\) converge vers \(l\) quand \(t\) tend vers \(t_0\) et on note : \[\overrightarrow{F} (t) \xrightarrow[t\rightarrow t_0]{}
\overrightarrow{l}\] lorsque \(\left\| \overrightarrow{F} (t) - \overrightarrow{l} \right\| \xrightarrow[t\rightarrow t_0]{} 0\).
(Caractérisation de la convergence par les fonctions coordonnées). Soit \(\overrightarrow{F}\) une fonction vectorielle donnée par le couple \((x,y)\) sur \(I\). Soit \(\overrightarrow{l}=(l_1,l_2)\) un vecteur de \(\mathbb{R}^2\). On a : \[\boxed{\overrightarrow{F} (t)
\xrightarrow[t\rightarrow t_0]{} \overrightarrow{l} \Longleftrightarrow\left\{\begin{array}{l} x(t) \xrightarrow[t\rightarrow t_0]{}
l_1\newline y(t) \xrightarrow[t\rightarrow t_0]{} l_2 \end{array}\right.}\]
On a la série d’équivalences : \[\begin{aligned}
& &\overrightarrow{F} (t) \xrightarrow[t\rightarrow t_0]{} \overrightarrow{l}\\
&\Longleftrightarrow& \sqrt{ \left(x\left(t\right) - l_1\right)^2+\left(y\left(t\right)-l_2\right)^2 } = || \overrightarrow{f} (t) - \overrightarrow{l} ||
\xrightarrow[t\rightarrow t_0]{} 0\\
&\Longleftrightarrow& \left(x\left(t\right) - l_1\right)^2+\left(y\left(t\right)-l_2\right)^2 \xrightarrow[t\rightarrow t_0]{} 0\\
&\Longleftrightarrow& \left\{\begin{array}{l} x(t) \xrightarrow[t\rightarrow t_0]{} l_1\newline y(t) \xrightarrow[t\rightarrow t_0]{} l_2\end{array}\right.\end{aligned}\] car une somme de deux nombres positifs est nulle si et seulement si ces deux nombres sont nuls.
Rappelons la définition suivante :
(Dérivabilité d’une fonction réelle). On dit qu’une fonction réelle \(f: I \rightarrow \mathbb{R}\) est dérivable en \(t_0\in I\) si il existe un réel \(l\) tel que : \[{\scriptstyle f(t)-f(t_0)\over\scriptstyle t-t_0}
\xrightarrow[t\rightarrow t_0]{} l\] Dans le cas où cette limite existe, on notera \(f'(t_0)=l\). De plus, on dira que \(f\) est dérivable sur \(I\) si \(f\) est dérivable en tout point \(t\) de \(I\) non situé à une extrémité de \(I\).
(Dérivabilité d’une fonction vectorielle). On dit qu’une fonction vectorielle \(\overrightarrow{F} : I \rightarrow \mathbb{R}^2, t \mapsto (x(t),y(t))\) est dérivable en \(t_0\in I\) si il existe \(\overrightarrow{l}=(l_1,l_2)\) un vecteur de \(\mathbb{R}^2\) tel que : \[{\scriptstyle\overrightarrow{F}(t)-\overrightarrow{F}(t_0)\over\scriptstyle t-t_0} \xrightarrow[t\rightarrow t_0]{} \overrightarrow{l}\] Dans le cas où cette limite existe, on note \(\overrightarrow{F}'(t_0)=l\).
(Dérivabilité d’une fonction vectorielle sur un intervalle). On dit qu’une fonction vectorielle \(\overrightarrow{F} : I \rightarrow \mathbb{R}^2, t \mapsto (x(t),y(t))\) est dérivable sur \(I\) si \(\overrightarrow{F}\) est dérivable en tout point \(t\) de \(I\) non situé à une extrémité de \(I\).
(Caractérisation par les fonctions coordonnées). Une fonction vectorielle \(\overrightarrow{F} : I \rightarrow \mathbb{R}^2, t \mapsto (x(t),y(t))\) est dérivable en \(t_0\in I\) si et seulement si les deux fonctions réelles qui la composent: \(x\) et \(y\) sont dérivables en \(t_0\). On a alors : \[\boxed{F'(t_0)=(x'(t_0),y'(t_0))}\]
Considérons la fonction vectorielle \[\overrightarrow{\theta}: \left\{ \begin{array}{ccl} I\setminus
\left\{t_0\right\} & \longrightarrow & \mathbb{R}^2 \\ t & \longmapsto & \dfrac{\overrightarrow{F}(t)-\overrightarrow{F}(t_0)}{t-t_0} \end{array} \right.\] ses fonctions coordonnées sont : \[\theta_1: \left\{ \begin{array}{ccl} I\setminus \left\{t_0\right\} & \longrightarrow & \mathbb{R} \\ t & \longmapsto & {\scriptstyle x(t)- x(t_0)\over\scriptstyle t-t_0} \end{array} \right. \quad \textrm{ et} \quad\theta_2: \left\{ \begin{array}{ccl} I\setminus \left\{t_0\right\} & \longrightarrow & \mathbb{R} \\ t & \longmapsto & {\scriptstyle y(t)- y(t_0)\over\scriptstyle t-t_0} \end{array} \right.\] En appliquant la proposition précédente, on a la série d’équivalences : \[\begin{aligned}
& & x \quad \textrm{ et} \quad y \textrm{ sont dérivables en } t_0\\
&\Longleftrightarrow& \textrm{ les fonctions coordonnées $\theta_1$ et $\theta_2$ de $\overrightarrow{\theta}$ vérifient } \theta_1 \left(t\right) \xrightarrow[t\rightarrow t_0]{} x'\left(t_0\right) \quad \textrm{ et} \quad\theta_2 \left(t\right) \xrightarrow[t\rightarrow t_0]{} y'\left(t_0\right)\\
&\Longleftrightarrow&\overrightarrow{\theta }\left(t\right) \xrightarrow[t\rightarrow t_0]{} \left(x'\left(t_0\right),y'\left(t_0\right)\right)\newline
&\Longleftrightarrow& \textrm{ $\overrightarrow{F}$ est dérivable en $t_0$ et } F'(t_0)=(x'(t_0),y'(t_0))\end{aligned}\]
De manière plus générale, on dira que:
(Fonction \(k\) fois dérivable, de classe \(\mathcal{C}^{k}\) ).
Une fonction \(\overrightarrow{F} : I \rightarrow R^2\) est dite \(k\) fois dérivable sur \(I\) si ses fonctions coordonnées le sont.
Une fonction \(\overrightarrow{F}: I \rightarrow R^2\) est dite de classe \(\mathcal{C}^{k}\) sur \(I\) si ses fonctions coordonnées sont \(k\) fois dérivables sur \(I\) et si sa dérivée \(k\)-ième est continue.
Dérivation du produit scalaire et du déterminant
(Dérivation du produit scalaire, du déterminant). Soient \(\overrightarrow{F}\) et \(\overrightarrow{G}\) deux applications définies sur \(I\), dérivables en \(t_0
\in I\) et à valeurs dans \(\mathbb{R}^2\). Alors les applications \[\left<\overrightarrow{F}|\overrightarrow{G}\right>: \left\{ \begin{array}{ccl} I & \longrightarrow & R \\ t & \longmapsto & \left<\overrightarrow{F}(t)|\overrightarrow{G}(t)\right> \end{array} \right. \quad \textrm{ et} \quad\mathop{\rm det}\left({\overrightarrow{F}},{\overrightarrow{G}}\right): \left\{ \begin{array}{ccl} I & \longrightarrow & R \newline t & \longmapsto & \mathop{\rm det}\left({\overrightarrow{F}(t)},{\overrightarrow{G}(t)}\right) \end{array} \right.\] sont dérivables en \(t_0\) et \[\boxed{\left(\left<\overrightarrow{F}|\overrightarrow{G}\right>\right)'(t_0)=\left<\overrightarrow{F}'(t_0)|\overrightarrow{G}(t_0)\right>+\left<\overrightarrow{F}(t_0)|\overrightarrow{G}'(t_0)\right> }\] \[\boxed{\left(\mathop{\rm det}\left(\overrightarrow{F},\overrightarrow{G}\right)\right)'(t_0)=\mathop{\rm det}\left(\overrightarrow{F}'(t_0),\overrightarrow{G}(t_0)\right)+\mathop{\rm det}\left(\overrightarrow{F}(t_0),\overrightarrow{G}'(t_0)\right)}\]
Notons \(\overrightarrow{F}=\left(f_1,f_2\right)\) et \(\overrightarrow{G}=\left(g_1,g_2\right)\). Comme \(F\) et \(G\) sont dérivables en \(t_0\), d’après le théorème [prop:12110016122009], il en est de même des fonctions \(f_1,f_2,g_1,g_2\). Soit \(t\in I\). Remarquons que \[\left<\overrightarrow{F}|\overrightarrow{G}\right>\left(t\right)= f_1\left(t\right)g_1\left(t\right)+ f_2\left(t\right)g_2\left(t\right)\] et la fonction \(\left<\overrightarrow{F}|\overrightarrow{G}\right>\) est donc dérivable en \(t_0\) par opérations sur les fonctions dérivables en \(t_0\) et à valeurs dans \(\mathbb{R}\). De plus : \[\begin{aligned}
\left(\left<\overrightarrow{F}|\overrightarrow{G}\right>\right)'(t_0)
&=&\left(f_1.g_1+ f_2.g_2\right)'\left(t_0\right)\\
&=& f_1'\left(t_0\right) g_1\left(t_0\right) + f_1\left(t_0\right) g_1'\left(t_0\right) +f_2'\left(t_0\right) g_2\left(t_0\right) +
f_2\left(t_0\right) g_2'\left(t_0\right) \newline
&=&
\left<\overrightarrow{f}'(t_0)|\overrightarrow{g}(t_0)\right>+\left<\overrightarrow{f}(t_0)|\overrightarrow{g}'(t_0)\right> .\end{aligned}\] La deuxième formule se prouve de même.
(Dérivation de la norme). Soit \(\overrightarrow{F}\) une fonction définie sur \(I\), dérivable en \(t_0 \in I\), à valeurs dans \({\mathbb{R}^2}\) et ne s’annulant pas. Alors l’application \(\left\|\overrightarrow{F}\right\|:I \rightarrow \mathbb{R}\) est dérivable en \(t_0\) et \[\boxed{\left(\left\|\overrightarrow{F}\right\|\right)'(t_0)=\dfrac{\left<\overrightarrow{F}'(t_0)|\overrightarrow{F}(t_0) \right>}{\left\|\overrightarrow{F} (t_0)\right\|}}\]
On sait que \(\left\|\overrightarrow{F}\right\|=\sqrt{\left<\overrightarrow{F}|\overrightarrow{F}\right>}\). D’après la proposition précédente \(t\mapsto \left<\overrightarrow{F}|\overrightarrow{F}\right>\) est dérivable en \(t_0\) et on sait que la fonction racine est dérivable sur \(\mathbb{R}_+^*\). Comme la fonction \(\overrightarrow{F}\) ne s’annule pas, il en est de même de \(t\mapsto \left<\overrightarrow{F}|\overrightarrow{F}\right>\left(t\right)\) et donc la fonction \(\left\|\overrightarrow{F}\right\|\) est dérivable en \(t_0\). De plus, grâce à la formule de dérivation et la symétrie du produit scalaire : \[\begin{aligned}
\left(\left\|\overrightarrow{F}\right\|\right)'(t_0)&=&\left(\sqrt{\left<\overrightarrow{F}|\overrightarrow{F}\right>}\right)'\left(t_0\right)
= \dfrac{\left(\left<\overrightarrow{F}|\overrightarrow{F}\right>\right)'\left(t_0\right) }{2\sqrt{ \left<\overrightarrow{F}|\overrightarrow{F}\right> } \left(t_0\right)}
= \dfrac{\left<\overrightarrow{F}'(t_0)|\overrightarrow{F}(t_0) \right>}{\left\|\overrightarrow{F} (t_0)\right\|}.\end{aligned}\]
Arcs paramétrés
Définitions
(Arc paramétré). On appelle arc paramétré ou courbe paramétrée un couple \(\gamma = (I, \overrightarrow{F})\) où \(I \subset \mathbb{R}\) est un intervalle et \(\overrightarrow{F} : I \mapsto \mathbb{R} [2]\) une application de classe \({\mathcal{C}}^[(k) ]{I, \mathbb{R} [2]}\).
(Support d’un arc paramétré). On appelle support (ou image) de l’arc paramétré \((I,\overrightarrow{F})\) l’ensemble des points du plan : \[\Gamma = \left\{ M \in \mathscr P~|~
\exists t \in I: ~~ \overrightarrow{OM}=\overrightarrow{F}(t) \right\}\] Pour tout \(t\in I\), on notera \(M(t)\) le point du support de l’arc \((I,\overrightarrow{F})\) tel que \(\overrightarrow{OM}(t)=\overrightarrow{F}(t)\).
Se donner une fonction \(f:I\to \mathbb{R}\) revient à se donner un arc paramétré \(\left(I,\overrightarrow{F}\right)\) où pour tout \(t\in I\), \(\overrightarrow{F}(t)=\left(t,f(t)\right)\).
L’étude d’un arc paramétré peut s’interpréter ainsi:
\(I\) est un intervalle de temps.
\(M(t)\) est un point mobile du plan dont la position à l’instant \(t\in I\) est donné par \(\overrightarrow{OM(t)}= \overrightarrow{F}(t)\).
Le support de l’arc paramétré \((I,\overrightarrow{F})\) est appelé trajectoire du mouvement.
Les vecteurs \(\overrightarrow{F'}(t)\) et \(\overrightarrow{F''}(t)\), si ils existent, sont respectivement appelés vecteur vitesse et vecteur accélération du point \(M\) à l’instant \(t\).
Étude locale d’un arc paramétrée
(Limite d’une famille de droites dans le plan). On dit qu’une famille de droites \((D_t)_{i \in I\setminus\{t_0\}}\) passant par un même point \(M\) admet une limite lorsque \(t \rightarrow t_0\) s’il existe une famille \((\overrightarrow{u}(t))_{ t \in I \setminus \{t_0\}}\) de vecteurs directeurs de ces droites possédant un vecteur limite \(\overrightarrow{l}\) non-nul lorsque \(t \rightarrow t_0\). La droite \(D = M + \mathop{\mathrm{Vect}}(\overrightarrow{l})\) s’appelle la limite de \((D_t)\).
(Tangente à un arc paramétré). Soit un arc paramétré \(\gamma = (I, \overrightarrow{F})\) et \(t_0 \in I\). On dit que l’arc admet une tangente au point \(M_0 = M(t_0) \in \Gamma\) si la famille de droites \(D_t = \bigl(M(t_0), M(t)\bigr)\) admet une limite lorsque \(t \rightarrow t_0\). La droite limite s’appelle la tangente à l’arc au point \(M_0\).
On définit de la même façon, avec les limites à droite ou à gauche, la notion de demi-tangente en un point.
Une conséquence de cette définition et de la remarque [rem_lien_fct_cb_param] est que si une fonction \(f\) est dérivable en \(t_0\in I\) alors le vecteur \((1,f'(t_0))\) est tangent au graphe de \(f\) en \((t_0,f(t_0))\).
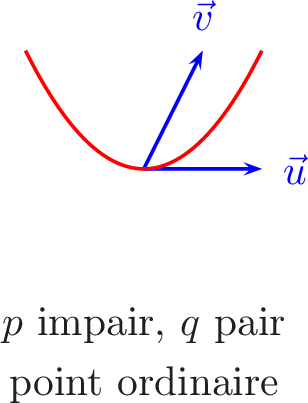
(Point régulier, stationnaire). Un point \(M = M(t_0)\) d’un arc paramétré est dit régulier lorsque \(\overrightarrow{F}'(t_0) \neq 0\). Sinon, on dit que c’est un point stationnaire.
(Tangente en un point régulier). Un arc paramétré possède une tangente en un point régulier \(M(t_0)\) : la droite passant par \(M(t_0)\) dirigée par le vecteur \(\overrightarrow{F}'(t_0)\).
Notons \[\overrightarrow{u} :
\left\{ \begin{array}{ccl} I\setminus \{t_0\} & \longrightarrow & \mathbb{R} [2] \newline t & \longmapsto & \dfrac{\overrightarrow{F}(t) -
\overrightarrow{F}(t_0)}{t - t_0} \end{array} \right.\] Pour \(t \neq t_0\), le vecteur \(\overrightarrow{u}(t)\) dirige la droite \((M(t_0)M(t))\) et \(\overrightarrow{u}(t) \xrightarrow[t \rightarrow t_0]{} \overrightarrow{F'}(t_0)
\neq \overrightarrow{0}\).
r20mm
(-0.1,-1)(2,0) (0,0)(-0.1,-1)(2,1) (0,0)(1,0)
Étude d’un point stationnaire avec des outils de terminale, première période
(Tangente en un point stationnaire).
Soit \(M(t_0)\) un point stationnaire d’une courbe paramétrée \((I,\overrightarrow{F})\) où \(\overrightarrow{F}\) est donnée par le couple de fonctions \((x,y)\) définies sur \(I\) .
si \(\boxed{\dfrac{y(t)-y(t_0)}{x(t)-x(t_0)} \xrightarrow[t\rightarrow t_0]{} m}\) où \(m\) est un réel alors la courbe admet en \(M(t_0)\) une tangente de pente \(m\).
si \(\boxed{\left| \dfrac{y(t)-y(t_0)}{x(t)-x(t_0)} \right| \xrightarrow[t\rightarrow t_0]{} +\infty}\) alors la courbe admet en \(M(t_0)\) une tangente verticale.
Soit \(\theta: \left\{ \begin{array}{ccl} I\setminus\left\{t_0\right\} & \longrightarrow & \mathbb{R}^2 \\ t & \longmapsto & \dfrac{y(t)-y(t_0)}{x(t)-x(t_0)
} \end{array} \right.\)
Si \(\theta\left(t\right) \xrightarrow[t\rightarrow t_0]{} m\) alors le vecteur \(\left(1,\theta\left(t\right)\right)\) dirige la droite \(\left(M\left(t_0\right)M\left(t\right)\right)\). En effet, un vecteur directeur de cette droite étant celui de coordonnées \(\left(x\left(t\right) - x\left(t_0\right),y\left(t\right) - y\left(t_0\right)\right)\) : \[\left| \begin{array}{cc} 1&x\left(t\right) - x\left(t_0\right)\newline \theta\left(t\right) & y\left(t\right) - y\left(t_0\right) \end{array} \right| = 0\] et \(\displaystyle{\lim_{t \rightarrow t_0}\theta\left(t\right)}=\left(1,m\right)\neq \left(0,0\right)\)
Si \(\theta\left(t\right) \xrightarrow[t\rightarrow t_0]{} +\infty\) alors on peut vérifier que le vecteur \(\left({\scriptstyle 1\over\scriptstyle\theta\left(t\right)},1\right)\) dirige la droite \(\left(M\left(t_0\right)M\left(t\right)\right)\) et on a : \(\displaystyle{\lim_{t \rightarrow t_0}\left({\scriptstyle 1\over\scriptstyle\theta\left(t\right)},1\right)}=\left(0,1\right)\neq \left(0,0\right)\)
Utilisons cette méthode pour calculer un vecteur tangent à la courbe \(\left(I,\overrightarrow{F}\right)\) avec \(I=\mathbb{R}\) et \(\overrightarrow{F}
\left(t\right)=\left(t^2,t^3\right)\) de la remarque [rem:14160016122009] en le point stationnaire de paramètre \(t=0\). On a : \[\begin{aligned}
\dfrac{y(t)-y(0)}{x(t)-x(0)}=\dfrac{t^3}{t^2}=t \xrightarrow[t\rightarrow 0]{}0 \end{aligned}\] donc la pente de la tangente en le point stationnaire \(\left(0,0\right)\) est \(0\). Cette droite est l’axe des abscisses.
Cette méthode n’est utilisable que si on sait déterminer la limite du quotient \({\scriptstyle y(t)-y(t_0)\over\scriptstyle x(t)-x(t_0)}\), ce qui ne sera pas toujours possible avec les outils dont vous disposez en début d’année.
Étude d’un point stationnaire avec les développements limités, seconde période
(Tangente en un point stationnaire). Si \(M(t_0)\) est un point stationnaire d’un arc \(\mathcal{C}^{k}\) et s’il existe \(p \leqslant k\) tel que \[\overrightarrow{F}'(t_0) = \dots =
\overrightarrow{F}^{(p-1)}(t_0) = 0, \overrightarrow{F}^{(p)}(t_0) \neq 0\] alors l’arc possède une tangente au point \(M(t_0)\) dirigée par le vecteur \(\overrightarrow{F}^{(p)}(t_0)\).
C’est une conséquence de la formule de Taylor-Young en \(t_0\) pour les fonctions vectorielles (il suffit d’utiliser la formule de Taylor-Young ([thm:taylor_young] page [thm:taylor_young]) pour les deux fonctions coordonnées) : \[\overrightarrow{F}(t) = \overrightarrow{F}(t_0) + (t-t_0) \overrightarrow{F'}(t_0) +
\dots + \dfrac{(t-t_0)^p}{p!} \overrightarrow{F^{(p)}}(t_0) + (t-t_0)^p
\overrightarrow{\varepsilon(t)}\] avec \(\overrightarrow{\varepsilon(t)} \xrightarrow[t \rightarrow t_0]{} \overrightarrow{0}\). Définissons alors la fonction \(\overrightarrow{u}\) en posant pour \(t\neq
t_0\), \[\overrightarrow{u(t)} = \dfrac{p!}{(t-t_0)^p}\bigl[\overrightarrow{F}(t) -
\overrightarrow{F}(t_0)\bigr] = \overrightarrow{F^{(p)}}(t_0) + p!
\overrightarrow{\varepsilon}(t)\] Pour \(t \neq t_0\), \(\overrightarrow{u(t)}\) dirige la droite \(M(t_0)M(t)\) et \(\overrightarrow{u}(t) \xrightarrow[t \rightarrow t_0]{} F^{(p)}(t_0) \neq \overrightarrow{0}\).
Cette méthode appliquée à la courbe \(\left(I,\overrightarrow{F}\right)\) avec \(I=\mathbb{R}\) et \(\overrightarrow{F}
\left(t\right)=\left(t^2,t^3\right)\) de la remarque [rem:14160016122009] en le point stationnaire de paramètre \(t=0\). donne \(F^{\left(2\right)}\left(t\right)=\left(3t,2\right)\) et donc un vecteur tangent à la courbe en le point stationnaire est celui de coordonnées \(\left(0,2\right)\).
Cette méthode peut être utilisée sans connaître les développements limités. Par contre, elle peut nécessiter un grand nombre de calculs avant de trouver un vecteur \(\overrightarrow{F}^{(p)}(t_0)=\left(x^{\left(p\right)}\left(t_0\right),y^{\left(p\right)}\left(t_0\right)\right)\) qui ne s’annule pas. Ces calculs sont grandement facilités, comme on le verra dans les exercices, avec les développements limités.
Le théorème suivant permet d’étudier localement l’allure d’une courbe au voisinage d’un point stationnaire sous des hypothèses très générales.
(Étude locale d’un point stationnaire). On suppose que la fonction \(\overrightarrow{F} : I \mapsto \mathbb{R} [2]\) est de classe \(\mathcal{C}^{k}\), et qu’il existe deux entiers \(1\leqslant p<q \leqslant k\) tels que :
\(\overrightarrow{F^{(p)}}(t_0)\) est le premier vecteur non-nul parmi \(\overrightarrow{F'}(t_0),\dots, \overrightarrow{F^{(p)}}(t_0)\).
\(q\) est le premier entier parmi \([\kern-0.127em[ p+1, q ]\kern-0.127em]\) tel que le système de vecteurs \((\overrightarrow{F^{(p)}}(t_0), \overrightarrow{F^{(q)}}(t_0))\) soit libre
Alors :
Le vecteur \(\overrightarrow{F^{(p)}}(t_0)\) dirige la tangente à la courbe au point \(M(t_0)\).
Pour \(t\neq t_0\), dans le repère \(\mathcal{R} = \bigl(M(t_0), \overrightarrow{F^{(p)}}(t_0), \overrightarrow{F^{(q)}}(t_0)\bigr)\), le point \(M(t)\) a pour coordonnées : \(M(t) \underset{\mathcal{R}}{\left|\begin{matrix} X(t) \\ Y(t) \end{matrix}\right.}\)
\(X(t)\underset{t \rightarrow t_0}{\sim} \dfrac{(t-t_0)^p}{p!}\), \(Y(t) \underset{t \rightarrow t_0}{\sim} \dfrac{(t-t_0)^q}{q!}\).
Écrivons la formule de Taylor-Young vectorielle en \(t_0\) à l’ordre \(q\) : \[\begin{aligned}
\overrightarrow{F}(t) &= \overrightarrow{F}(t_0) +
\dfrac{(t-t_0)^p}{p!} \overrightarrow{F^{(p)}(t_0)}
+ \dfrac{(t-t_0)^{p+1}}{(p+1)!} \overrightarrow{F^{(p+1)}}(t_0) + \dots
\\
&= + \dfrac{(t-t_0)^q}{q!} \overrightarrow{F^{(q)}}(t_0) + (t-t_0)^q
\overrightarrow{\varepsilon}(t)
\end{aligned}\] Mais comme les vecteurs \(\overrightarrow{F^{(p+1)}}(t_0), \dots \overrightarrow{F^{(q-1)}}(t_0)\) sont tous proportionnels à \(\overrightarrow{F^{(p)}}(t_0)\), on peut écrire \(F^{(k)}(t_0) = \alpha_k F^{(p)}(t_0)\) pour \(k \in
[\kern-0.127em[ p+1, q-1 ]\kern-0.127em]\) et comme \(\bigl(\overrightarrow{F^{(p)}}(t_0),
\overrightarrow{F^{(q)}}(t_0) \bigr)\) forme une base de \(\mathbb{R} [2]\), on peut décomposer le vecteur \(\overrightarrow{\varepsilon(t)}\) sur cette base : \[\overrightarrow{\varepsilon(t)} = \lambda(t) \overrightarrow{F^{(p)}}(t_0) + \mu(t)
\overrightarrow{F^{(q)}}(t_0)\] avec \(\lambda(t), \mu(t) \xrightarrow[t \rightarrow t_0]{} 0\). Alors : \[\begin{aligned}
\overrightarrow{F(t)}-\overrightarrow{F(t_0)} &=
\dfrac{(t-t_0)^p}{p!}\bigl[1 + (t-t_0)\alpha_{p+1} + \dots \\
&+ (t-t_0)^{q-1-p}\alpha_{q-1} + p!(t-t_0)^q \lambda(t)\bigr]
\overrightarrow{F^{(p)}}(t_0) \\
&+\dfrac{(t-t_0)^q}{q!}\bigl[1 +
q!\mu(t)\bigr] \overrightarrow{F^{(q)}}(t_0)
\end{aligned}\] Puisque \(\overrightarrow{M(t_0)M(t)} = \overrightarrow{F}(t)-\overrightarrow{F}(t_0)\), on en déduit l’expression des coordonnées du point \(M(t)\) dans le repère \(\mathcal{R}\) : \[\begin{aligned}
X(t) &= \dfrac{(t-t_0)^p}{p!}\bigl[1 + (t-t_0)\alpha_{p+1} + \dots \\
&+ (t-t_0)^{q-1-p}\alpha_{q-1} + p!(t-t_0)^q \lambda(t)\bigr] \\
&\underset{t \rightarrow t_0}{\sim} \dfrac{(t-t_0)^p}{p!}
\end{aligned}\] \[\begin{aligned}
Y(t) &= \dfrac{(t-t_0)^q}{q!}\bigl[1 +
q!\mu(t)\bigr] \newline
&\underset{t \rightarrow t_0}{\sim} \dfrac{(t-t_0)^q}{q!}
\end{aligned}\] L’équivalent donne le signe de \(X(t)\) et \(Y(t)\) au voisinage de \(t_0\). On obtient donc localement la position du point \(M(t)\) dans un quart de plan lorsque \(t < t_0\) et \(t > t_0\) d’où l’étude géométrique résumée sur la figure [fig:position_locale_tangente_courbe_param].
(1). En pratique, pour étudier un point stationnaire \(M(t_0)\), on effectue un développement limité de \(x(t)\) et \(y(t)\) au voisinage de \(t_0\) et on adapte l’idée de la démonstration précédente. Puisque le point \(M(t_0)\) est stationnaire, \(x'(t_0) = y'(t_0) = 0\) et donc le coefficient de \((t-t_0)\) sera nul dans les développements limités de \(x\) et \(y\). Puisqu’il nous faut deux vecteurs indépendants \(F^{(p)}(t_0)\) et \(F^{(q)}(t_0)\), il faut au moins un DL à l’ordre \(3\) des deux fonctions \(x\) et \(y\).
\[\begin{cases}
x(t) &= 3 \cos(t) - 2 \sin^3(t) \\
y(t) &= \cos(4t)
\end{cases}\] pour \(t \in [0, 2\pi]\). Commençons par chercher les points stationnaires : \[\begin{cases}
x'(t) &= -3\sin(t)\bigl[1 + \sin(2t)\bigr] \\
y'(t) &= -4\sin(4t)
\end{cases}\] \(x'\) et \(y'\) s’annulent simultanément en \(t = 0\) et \(t = 3\pi/4\). Étudions le point stationnaire \(M(0)\). Pour cela, effectuons un DL à l’ordre \(3\) : \[\begin{cases}
x(t) &= 3 - \dfrac{3}{2} t^2 - 2 t^3 + \underset{t \rightarrow 0}{o}\left(t^3\right) \\
y(t) &= 1 - 8t^2 + \underset{t \rightarrow 0}{o}\left(t^3\right)
\end{cases}\] d’où le DL vectoriel : \[\overrightarrow{F}(t) = \underbrace{\begin{pmatrix} 3 \\ 1
\end{pmatrix}}_{\overrightarrow{F}(0)} + t^2
\underbrace{\begin{pmatrix}
-3/2 \\ -8\end{pmatrix}}_{\overrightarrow{u}} +
t^3 \underbrace{\begin{pmatrix} -2
\newline 0 \end{pmatrix} }_{\overrightarrow{v}} + \underset{t \rightarrow 0}{o}\left(t^3\right)\] Les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) ne sont pas liés et dans le repère \(\mathcal{R} = (M(0), \overrightarrow{u}, \overrightarrow{v})\), le point \(M(t)\) a pour coordonnées \(X(t)\) et \(Y(t)\) avec \(X(t) \underset{t \rightarrow 0}{\sim} t^2\) et \(Y(t) \underset{t \rightarrow 0}{\sim} t^3\). On en déduit l’allure locale de la courbe au voisinage de \(M(0)\) : c’est un point de rebroussement de première espèce.
L’étude du point stationnaire \(M(3\pi/4)\) s’effectue de même.
Branches infinies des courbes paramétrées
(Branche infinie). On dit que l’arc \((I,\overrightarrow{F})\) possède une branche infinie en \(t_0\) lorsque \(\lVert \overrightarrow{F}(t) \rVert_{ } \xrightarrow[t \rightarrow t_0]{} +\infty\).
Si \(\lim_{t \rightarrow t_0} \left|x(t)\right|=+\infty\) ou si \(\lim_{t \rightarrow t_0} \left|y(t)\right|=+\infty\) alors l’arc \((I,f)\) possède une branche infinie en \(t_0\).
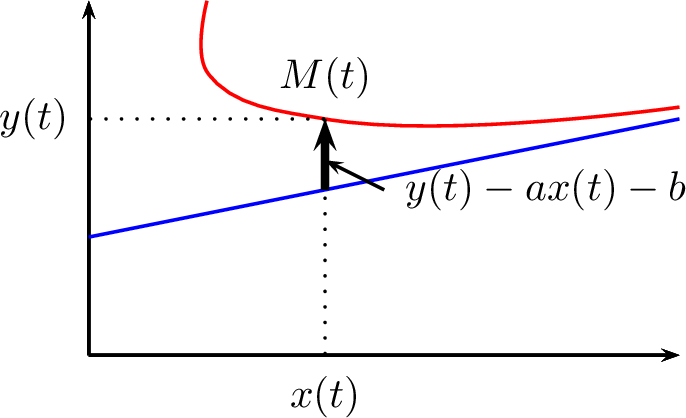
(Droite asymptote). Soit \((I,\overrightarrow{F})\) un arc paramétré possédant une branche infinie en \(t_0\in I\). On dit que la droite \(\mathscr D\) est asymptote à l’arc \((I,\overrightarrow{F})\) en \(t_0\) si \(d(M(t), \mathscr D) \xrightarrow[t \rightarrow t_0]{} 0\).
(Caractérisation pratique d’une droite asymptote). Soit \((I,\overrightarrow{F})\) un arc paramétré possédant une branche infinie en \(t_0\in I\). La droite \(\mathscr D\) d’équation \(a~x+ b~y +c=0\) est asymptote à l’arc \((I,\overrightarrow{F})\) en \(t_0\) si et seulement si \[\boxed{ a~x(t)+ b~y(t) +c \xrightarrow[t \rightarrow t_0]{} 0}\].
Soit \(\mathscr D\) une droite affine d’équation cartésienne : \(ax+by+c=0\). La distance du point \(M(t) \underset{R}{\left|\begin{matrix} x(t) \newline y(t) \end{matrix}\right.}\) vaut : \[d(M(t), \mathscr D) = \dfrac{\lvert ax(t) + b y(t) + c \rvert }{\sqrt{a^2+b^2}}\] Cette distance tend vers \(0\) si et seulement si \(ax(t) + by(t) + c
\xrightarrow[t \rightarrow t_0]{} 0\).
(Pour déterminer la droite asymptote à une branche infinie).
Une seule des deux applications coordonnées de \(f\) tend vers l’infini en valeur absolue quand \(t\) tend vers \(t_0\):
Si \(x(t) \xrightarrow[t\rightarrow t_0]{} l \in \mathbb{R}\) et \(\left| y(t) \right | \xrightarrow[t\rightarrow t_0]{} +\infty\) alors la droite d’équation \(x=l\) est asymptote à la courbe et le signe de \(x(t)-l\) détermine la position de la courbe par rapport à l’asymptote.
Si \(\left|x(t)\right| \xrightarrow[t\rightarrow t_0]{} +\infty\) et \(y(t) \xrightarrow[t\rightarrow t_0]{} l \in \mathbb{R}\) alors la droite d’équation \(y=l\) est asymptote à la courbe et le signe de \(y(t)-l\) détermine la position de la courbe par rapport à l’asymptote.
Les deux applications coordonnées de \(f\) tendent vers l’infini en valeur absolue quand \(t\) tend vers \(t_0\):
Si \(\left|x(t)\right | \xrightarrow[t\rightarrow t_0]{} +\infty\) et \(\left| y(t) \right | \xrightarrow[t\rightarrow t_0]{} +\infty\), on forme le quotient \({\scriptstyle y(t)\over\scriptstyle x(t)}\) et on cherche la limite de ce quotient quand \(t\) tend vers \(t_0\).
Si \({\scriptstyle y(t)\over\scriptstyle x(t)} \xrightarrow[t\rightarrow t_0]{} a \in \mathbb{R}^*\): on forme alors \(y(t)-a~x(t)\) et si cette quantité tend vers une limite finie \(b\) alors la droite d’équation \(y=a~x+b\) est asymptote à la courbe en \(t_0\). La position de la courbe par rapport à l’asymptote est donnée par le signe de \(y(t)-a~x(t)-b\).
Si \(\left|{\scriptstyle y(t)\over\scriptstyle x(t)}\right| \xrightarrow[t\rightarrow t_0]{} +\infty\), on dit que la courbe possède une branche parabolique \((Oy)\).
Si \({\scriptstyle y(t)\over\scriptstyle x(t)} \xrightarrow[t\rightarrow t_0]{} 0\), on dit que la courbe possède une branche parabolique \((Ox)\)
Intéressons nous à la courbe donnée par \[\begin{cases}
x\left(t\right)&= \dfrac{1}{t-1} \\ y\left(t\right)&=\dfrac{t^2+1}{t-1}\end{cases}.\] Elle présente des branches infinies quand \(t\rightarrow {1^{\pm}}\) et quand \(t\rightarrow
\pm \infty\).
r50mm
(-2,-4)(2,3) (0,0)(-3,-6)(2,10)
Comme \(x\left(t\right)\xrightarrow[t\rightarrow +\infty]{}0\) et \(y\left(t\right)\xrightarrow[t\rightarrow +\infty]{}+\infty\) alors la droite d’équation \(x=0\) est asymptote à la courbe quand \(t\rightarrow +\infty\).
On montre de même que la droite d’équation \(x=0\) est asymptote à la courbe quand \(t\rightarrow -\infty\).
On forme le quotient \(y\left(t\right)/x\left(t\right)\) et on cherche sa limite quand \(t\rightarrow 1^+\) : \[\dfrac{y\left(t\right)}{x\left(t\right)}= t^2+1=\xrightarrow[t\rightarrow 1]{} 2\]
On cherche maintenant la limite de \(y\left(t\right)-2x\left(t\right)\) quand \(t\rightarrow 1\) : \[y\left(t\right)-2x\left(t\right)= \dfrac{t^2-1}{t-1}=t+1 \xrightarrow[t\rightarrow 1]{}2\] donc la droite d’équation \(y=2x+2\) est asymptote à la courbe quand \(t\rightarrow 1^+\).
On cherche la position de la courbe relativement à l’asymptote. Pour ce faire, on étudie le signe de : \[y\left(t\right)-2x\left(t\right)-2 = t-1 \geqslant 0 \textrm{ si } t \geqslant 1.\] Donc la courbe est au dessus de l’asymptote quand \(t\rightarrow 1^+\).
La même étude montre que la droite d’équation \(y=2x+2\) est asymptote à la courbe quand \(t\rightarrow 1^-\) et que la courbe est en dessous de l’asymptote dans ce cas.
Par définition, dire qu’une droite est asymptote à la branche infinie quand \(t\rightarrow t_0\) d’une courbe paramétrée signifie que la courbe s’approche infiniment près de la droite quand \(t\rightarrow t_0\). Quand ce phénomène se produit, on sait mieux représenter le support de la courbe étudiée. Malheureusement toutes les branches infinies n’ont pas la même croissance et celles dites paraboliques ne s’approchent pas d’une droite quand \(t\rightarrow t_0\). Par contre on peut parfois trouver des courbes simples qui vont être asymptotes à cette branche parabolique, voir à ce sujet l’exemple [exp:0227143049].
Lorsque \(x(t)\) et \(y(t)\) tendent toutes les deux vers l’infini, le plus rapide pour étudier la branche infinie consiste à effectuer un développement asymptotique de ces deux fonctions lorsque \(t \rightarrow t_0\) à la précision d’un terme significatif qui tend vers \(0\). On essaie alors de faire une combinaison linéaire des fonctions \(x(t)\) et \(y(t)\) pour éliminer les termes tendant vers l’infini. Si on trouve une relation du type \[y(t)=ax(t)+b+c(t-t_0)^k + o\left( (t-t_0)^k \right)\] on en déduit que la droite \(y=ax+b\) est asymptote à la courbe et la position locale de la courbe par rapport à son asymptote se déduit du signe de \(c\) et de la parité de \(k\).
Considérons la courbe paramétrée définie par : \[\begin{cases}
x(t) &= \dfrac{t^3}{t^2-9} \\[0.3cm]
y(t) &= \dfrac{t^2-2t}{t-3}
\end{cases}\] Elle présente des branches infinies lorsque \(t \rightarrow \pm \infty\), \(t
\rightarrow \pm 3\).
\(t \rightarrow -3\) : \(x(t) \xrightarrow[t \rightarrow -3]{} +\infty\) et \(y(t) \xrightarrow[t \rightarrow -3]{} -5/2\) donc la droite d’équation \(y = -5/2\) est asymptote.
\(t \rightarrow \pm \infty\) : effectuons un développement asymptotique : \[\begin{aligned} x(t) &= t + \dfrac{9}{t} + \underset{t \rightarrow \pm infty}{o}\left(1/t\right) \\ y(t) &= t + 1 + \dfrac{3}{t} + \underset{t \rightarrow \pm infty}{o}\left(1/t\right) \end{aligned}\] Pour éliminer le terme divergent, il suffit d’effectuer la combinaison linéaire : \[y(t) - x(t) - 1 = \dfrac{-6}{t} + \underset{t \rightarrow \pm infty}{o}\left(1/t\right)\] On en déduit d’une part que la droite d’équation \(y = x + 1\) est asymptote. D’autre part, la quantité \(y(t) - x(t) - 1\) représente la mesure algébrique verticale entre la droite et \(M(t)\). Par conséquent, lorsque \(t \rightarrow +\infty\), la courbe est située localement au dessous de l’asymptote et lorsque \(t \rightarrow -\infty\), elle est située localement au dessus.
\(t \rightarrow 3\), \[\begin{aligned} x(t) &= \dfrac{9}{2(t-3)} + \dfrac{15}{4} + \dfrac{7}{8}(t-3) + \underset{t \rightarrow 3}{o}\left((t-3)\right) \newline y(t) &= \dfrac{3}{t-3} + 4 + (t-3) \end{aligned}\] Éliminons les termes divergents : \[y(t) - \dfrac{2}{3} x(t) = \dfrac{3}{2} + \dfrac{5}{12}(t-3) + \underset{t \rightarrow 3}{o}\left((t-3)\right)\] On en déduit que la droite d’équation \(y = \dfrac{2}{3}x + \dfrac{3}{2}\) est asymptote à la courbe. Lorsque \(t \rightarrow 3^{-}\), la courbe est située localement en dessous de son asymptote. Lorsque \(t \rightarrow 3^{+}\), elle est située localement au dessus.
Cette méthode du développement asymptotique permet également de détecter d’autres courbes asymptotes.
\[\begin{cases} x(t) &= \dfrac{\sin t + 1}{t} \newline[0.3cm] y(t) &= \dfrac{\cos t}{t^2} \end{cases}\] Étudions la branche infinie \(t \rightarrow 0\) en utilisant Maple :
> x := (sin(t)+1)/t;
> y := cos(t) / t^2;
> series(x, t = 0, 2);
-1 2
t + 1 + O(t )
> series(y, t = 0, 2);
-2 2
t - 1/2 + O(t )Pour faire disparaître le terme en \(1/t^2\), considérons \(y(t) - x(t)^2\) :
> series(y - x^2, t = 0, 2);
-1 2
- 2 t - 3/2 + 1/3 t + O(t )Pour faire ensuite disparaitre le terme en \(1/t\), réutilisons \(x(t)\) :
> series(y - x^2 + 2*x, t = 0, 2);
2
1/2 + 1/3 t + O(t ) Puisque \[y(t) - x(t)^2 + 2x(t) - \dfrac{1}{2} \underset{t \rightarrow 0}{\sim}
\dfrac{t}{3},\] on en déduit que la parabole d’équation \(y = x^2-2x + 1/2\) est asymptote à notre courbe. Lorsque \(t \rightarrow 0^+\), la courbe est située localement au dessus de la parabole et lorsque \(t \rightarrow 0^-\), elle est située localement en dessous.
En trait pointillé le support de la courbe paramétrée, en trait plein le graphe de la parabole asymptote.
Étude complète et tracé d’une courbe paramétrée
(Plan d’étude d’une courbe paramétrée).
Déterminer le domaine de définition des deux fonctions \(x\) et \(y\).
Étudier les symétries éventuelles.
Dresser le tableau de variations des fonctions \(x\) et \(y\) et repérer dans ce tableau les points stationnaires, les points à tangente horizontale ou verticale et les branches infinies.
Étudier les points stationnaires.
Étudier les branches infinies.
Tracé sommaire de la courbe. Il est inutile d’utiliser la calculatrice pour reporter des points, il suffit de placer les asymptotes éventuelles, de mettre en évidence les points stationnaires et d’avoir l’allure globale de la courbe.
Le point \(2\) est très important et permet bien souvent de restreindre l’étude à un intervalle plus petit. Pour cela, on interprète géométriquement la position du point \(M(\varphi(t))\) par rapport au point \(M(t)\) où \(\varphi\) est une certaine transformation. Voyons quelques exemples courants :
Si \(x(t+T) = x(t)\) et \(y(t+T) = y(t)\), le point \(M(t+T)\) est le même que le point \(M(t)\). On aura tracé toute la courbe si on restreint l’étude au paramètre \(t\) qui varie dans un intervalle de la forme \([a, a+T[\).
Si \(x(-t) = x(t)\) et \(y(-t) = -y(t)\), le point \(M(-t)\) est le symétrique orthogonal du point \(M(t)\) par rapport à l’axe \((Ox)\). Il suffit de tracer la courbe pour \(t \in [0, +\infty[\) et de compléter le dessin final par une symétrie par rapport à \((Ox)\).
Si \(x(-t) = -x(t)\) et \(y(-t) = -y(t)\), le point \(M(-t)\) est le symétrique du point \(M(t)\) par rapport à l’origine. Il suffit d’étudier la courbe pour \(t \in [0, +\infty[\) et de compléter le tracé par une symétrie de centre l’origine.
Si \(x(1/t) = -x(t)\) et \(y(1/t) = y(t)\), les points \(M(1/t)\) et \(M(t)\) sont symétriques par rapport à \((Oy)\). Si on trace la portion de courbe pour \(t \in ]0, 1]\), la portion correspondant à \(t \in [1, +\infty[\) s’en déduit par une symétrie par rapport à l’axe \((Oy)\).
Étudier la courbe paramétrée \[\left\{ \begin{matrix}
x(t) = \tan t + \sin t \newline
y(t) = \dfrac{1}{\cos t}
\end{matrix} \right.\]
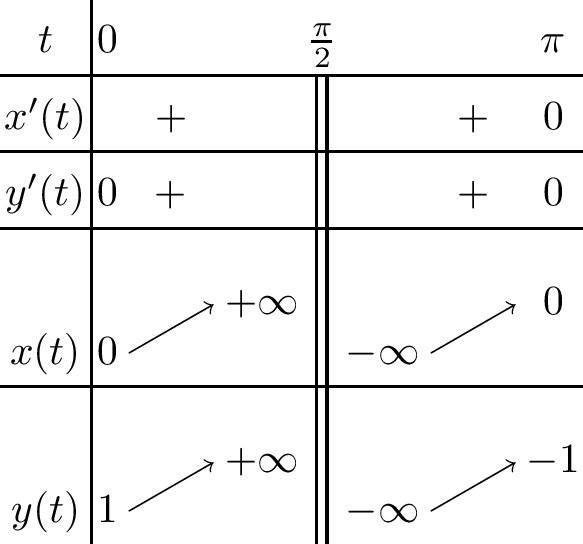
Les fonctions \(x\) et \(y\) sont définies sur \(\mathbb{R} \setminus \{k\pi + \pi /2; k \in \mathbb{Z} \}\).
Restriction de l’intervalle d’étude. On remarque que \(x(t+2\pi)= x(t)\) et \(y(t+2\pi)=y(t)\). Donc \(M(t + 2\pi) = M(t)\). Il suffit de faire l’étude de la courbe sur un intervalle \([\alpha, \alpha + 2\pi]\). De plus, \(x(-t) = - x(t)\) et \(y(-t) = y(t)\). Le point \(M(-t)\) est donc le symétrique du point \(M(t)\) par rapport à l’axe \(Oy\). Il suffit donc de faire l’étude sur \([0, \pi]\) et de compléter le tracé de la courbe par une symétrie par rapport à la droite \(Oy\).
Variations. On calcule \[x'(t) = \dfrac{\cos^3 t + 1}{\cos^2 t} \quad y'(t) = \dfrac{\sin t}{\cos^2 t}\] D’où le tableau de variations :
On remarque le point \(M(0)\) qui est à tangente horizontale, un point stationnaire \(M(\pi)\) et une branche infinie en \(t=\pi /2\).
Étude du point stationnaire.
Sans les développements limités : \[\dfrac{y\left(t\right)-y\left(\pi\right)}{x\left(t\right)-x\left(\pi\right)}=\dfrac{{\scriptstyle 1\over\scriptstyle\cos t}+1}{\tan t + \sin t} = \dfrac{1+\cos t}{\sin t\left(1+\cos t\right)}=\dfrac{1}{\sin t} \xrightarrow[t\rightarrow \pi^-]{}+\infty\] donc la courbe admet une tangente verticale en le point stationnaire de paramètre \(t=\pi\).
Avec les développements limités : Posons \(h = t - \pi\), et faisons un \(DL(0, 3)\) : \[\widetilde{x}(h) = \dfrac{h^3}{2} + o(h^3), \quad \widetilde{y}(h) = -1 - \dfrac{h^2}{2} + o(h^3)\] d’où l’on tire \[F(h) = \begin{pmatrix}0\\-1\end{pmatrix} + \dfrac{h^2}{2}\begin{pmatrix}0\\-1\end{pmatrix} +\dfrac{h^3}{2}\begin{pmatrix}1\newline0\end{pmatrix} + o(h^3)\] Dans le repère \(\mathcal{R} = (M(\pi), \overrightarrow{u}, \overrightarrow{v})\) où \(\overrightarrow{u} = (0,-1)\) et \(v=(1,0)\), le point \(M(t)\) a pour coordonnées \(\bigl(X(t), Y(t)\bigr)\) avec \(X(t) \sim (t-\pi)^2/2\) et \(Y(t) \sim (t-\pi)^3/2\) lorsque \(t \rightarrow \pi\). On en déduit que le point \(M(\pi)\) est un point de rebroussement de première espèce à tangente verticale.
Étude de la branche infinie.
Sans les développements limités : On forme le quotient \[\dfrac{y\left(t\right)}{x\left(t\right)}= \dfrac{1}{\sin t\left(1+\cos t\right)}\xrightarrow[t\rightarrow \pi/2]{}1.\] Ensuite, on calcule : \[y\left(t\right)-x\left(t\right) = \dfrac{1-\sin t}{\cos t} - \sin t \xrightarrow[t\rightarrow \pi/2]{}-1\] car \(\sin\) et \(\cos\) sont dérivables en \(\pi/2\) donc pour leurs taux d’accroissements respectifs en \(\pi/2\), on a : \[\dfrac{\sin t-1}{t-\pi/2} \xrightarrow[t\rightarrow \pi/2]{} \cos{\scriptstyle\pi\over\scriptstyle 2}=0 \quad \textrm{ et} \quad\dfrac{\cos t }{t-\pi/2}\xrightarrow[t\rightarrow \pi/2]{} -\sin{\scriptstyle\pi\over\scriptstyle 2}=-1\] donc \[\dfrac{1-\sin t}{\cos t} = -\dfrac{\dfrac{\sin t-1}{t-\pi/2}}{\dfrac{\cos t }{t-\pi/2}}\xrightarrow[t\rightarrow \pi/2]{} 0.\] Enfin, on étudie la position de la courbe par rapport à l’asymptote d’équation \(y=x-1\) : \[y\left(t\right)-x\left(t\right)+1= \dfrac{\left(1-\sin t\right)\left(1+\cos t\right)}{\cos t}\] qui est du signe de \(\cos t\). Donc lorsque \(t\rightarrow {\pi/2}^{+}\), la courbe arrive sous l’asymptote , et lorsque \(t\rightarrow {\pi/2}^{-}\), la courbe arrive sur l’asymptote.
Avec les développements limités : Lorsque \(t\rightarrow \pi /2\), en posant \(h = t - \pi /2\), on effectue un développement asymptotique des deux fonctions : \[\widetilde{x}(h) = x(\pi/2 + h) = -\dfrac{1}{\tan h} + \cos(h) = -\dfrac{1}{h(1 + h^2/3 + o(h^2))} + 1 + o(h) = -\dfrac{1}{h} + 1 + \dfrac{h}{3} + o(h)\] \[\widetilde{y}(h) = -1/\sin h = -\dfrac{1}{h} - \dfrac{h}{6} + o(h)\] Et alors \[\widetilde{y}(h) - \widetilde{x}(h) + 1 = -h/2 + o(h)\] ce qui montre que \(y(t) - x(t) + 1 \sim - (t-\pi/2)/2\) lorsque \(t \rightarrow \pi/2\). Par conséquent, la droite d’équation \(y = x - 1\) est asymptote à la courbe. Lorsque \(t\rightarrow {\pi/2}^{+}\), la courbe arrive sous l’asymptote à gauche, et lorsque \(t\rightarrow {\pi/2}^{-}\), la courbe arrive sur l’asymptote à droite.
L’astroïde est la courbe paramétrée définie par : \[\begin{cases}
x(t) &= a \cos^3 t \newline
y(t) &= a \sin^3 t
\end{cases}\]
Les deux fonctions sont définies sur \(\mathbb{R}\).
Symétries :
\(x(t+2\pi) = x(t)\), \(y(t+2\pi) = y(t)\) donc \(M(t+2\pi) = M(t)\). Il suffit de tracer la courbe pour \(t \in [t_0, t_0+2\pi]\).
\(x(t+\pi) = -x(t)\), \(y(t+\pi) = -y(t)\) donc le point \(M(t+\pi)\) est le symétrique du point \(M(t)\) par rapport à l’origine. Il suffit de tracer la courbe pour \(t \in [t_0, t_0+\pi]\) et de compléter le dessin par une symétrie centrale pour obtenir toute la courbe.
\(x(-t)=x(t)\), \(y(-t) = -y(t)\) donc \(M(-t)\) est le symétrique de \(M(t)\) par rapport à l’axe \((Ox)\). Il suffit de faire l’étude sur \([0, \pi/2]\) puis de compléter par une symétrie.
\(x(\pi/2-t) = y(t)\), \(y(\pi/2-t)=x(t)\) donc le point \(M(\pi/2-t)\) est le symétrique du point \(M(t)\) par rapport à la première bissectrice. Il suffit finalement de faire l’étude pour \(t \in [0, \pi/4]\), de compléter le tracé par des symétries par rapport à la première bissectrice, l’axe \((Ox)\) et l’origine pour obtenir la courbe complète.
Variations : \[\begin{cases} x'(t) &= -3a\cos^2 t \sin t \\ y'(t) &= 3a \sin^2 t \cos t \end{cases}\]
On remarque que le point \(M(0)\) est stationnaire. Il n’y a pas de branche infinie.
Étude du point stationnaire La première méthode est ici inutilisable car la limite ne peut pas se calculer avec les techniques usuelles. Effectuons un développement limité à l’ordre \(3\) : \[\begin{cases} x(t) &= a - \dfrac{3}{2} a t^2 + \underset{t \rightarrow 0}{o}\left(t^3\right) \\ y(t) &= at^3 + \underset{t \rightarrow 0}{o}\left(t^3\right) \end{cases}\] d’où \[\overrightarrow{F}(t) = \begin{pmatrix} a \\ 0 \end{pmatrix} + t^2 \underbrace{ \begin{pmatrix} -3a/2 \\ 0 \end{pmatrix}}_{\overrightarrow{u}} + t^3 \underbrace{ \begin{pmatrix} 0 \newline a \end{pmatrix}}_{\overrightarrow{v}} + \underset{t \rightarrow 0}{o}\left(t^3\right)\] Les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) étant indépendants, dans le repère \((M(0), \overrightarrow{u}, \overrightarrow{v})\), le point \(M(t)\) a pour coordonnées \(X(t) \underset{t \rightarrow 0}{\sim} t^2\) et \(Y(t) \underset{t \rightarrow 0}{\sim} t^3\). On en déduit que le point \(M(0)\) est un point de rebroussement de première espèce à tangente horizontale.
Tracé :
Une roue de rayon \(R>0\) roule sans glisser sur une route horizontale. Déterminons la trajectoire d’un point situé sur sa périphérie. Notons \(C(t)\) le centre de la roue et \(t\) l’angle entre la verticale et le vecteur \(\overrightarrow{C(t)M(t)}\). La roue roule sans glisser donc si le centre à l’instant \(t\) se trouve à l’abscisse \(x_C\), on a \(x_C = Rt\). On en déduit que \(C(t) \underset{ }{\left|\begin{matrix} Rt \\ R \end{matrix}\right.}\) puis comme \(\overrightarrow{C(t)M(t)} \underset{ }{\left|\begin{matrix} -R\sin t \\
-R \cos t \end{matrix}\right.}\) on obtient l’équation paramétrique de la courbe qui s’appelle la cycloïde : \[\begin{cases}
x(t) &= R(t - \sin t) \\
y(t) &= R(1-\cos t)
\end{cases}\]
Les fonctions \(x\) et \(y\) sont définies sur \(\mathbb{R}\).
Symétries : puisque \(x(t+2\pi) = x(t) + 2R\pi\), \(y(t+2\pi) = y(t)\), le point \(M(t+2\pi)\) se déduit du point \(M(t)\) par une translation de vecteur \(\overrightarrow{V} = (2R\pi, 0)\). Il suffit donc de tracer la courbe pour \(t \in [0, 2\pi]\) et on complète le tracé par une infinité de translations de vecteur \(\overrightarrow{V}\). Puisque \(x(-t) = -x(t)\) et \(y(-t) = y(t)\), le point \(M(-t)\) est le symétrique du point \(M(t)\) par rapport à l’axe \((Oy)\). Il suffit donc d’étudier la courbe pour \(t \in [0, \pi]\) et de compléter par une symétrie par rapport à \((Oy)\).
Variations : \[\begin{cases} x'(t) &= R(1-\cos t) \\ y'(t) &= R\sin t \end{cases}\]
On remarque que le point \(M(0)\) est stationnaire et que le point \(M(\pi)\) est à tangente horizontale.
Étude du point stationnaire : Là encore, la première technique est peu commode car elle aboutit à une limite difficile à calculer avec les méthodes usuelles. On effectue alors un DL à l’ordre \(3\), \[\overrightarrow{F}(t) = \begin{pmatrix} 0 \\ 0 \end{pmatrix} + t^2 \underbrace{ \begin{pmatrix} 0 \\ R/2 \end{pmatrix} }_{\overrightarrow{u}} + t^3 \underbrace{\begin{pmatrix} R/6 \newline 0 \end{pmatrix}}_{\overrightarrow{v}} + \underset{t \rightarrow 0}{o}\left(t^3\right)\] On en déduit que le point \(M(0)\) est un point de rebroussement de première espèce à tangente verticale.
Tracé :
Etude d’une courbe polaire \(\rho= f(\theta)\).
Notations
Il peut être plus commode d’étudier une courbe non pas en coordonnées cartésiennes, mais en coordonnées polaires car elle s’exprime parfois ainsi plus facilement. Nous allons expliquer ici comment mener cette étude.
On définit les fonctions vectorielles : \[\overrightarrow{u}(\theta)=\cos\theta \overrightarrow{\imath} + \sin\theta\overrightarrow{\jmath}, \quad \overrightarrow{v}(\theta)=-\sin\theta\overrightarrow{\imath}+\cos\theta\overrightarrow{\jmath}\] et on remarque que : \[\dfrac{d\overrightarrow{u}}{d\theta}=\overrightarrow{v}, \quad \dfrac{d\overrightarrow{v}}{d\theta}=-\overrightarrow{u}\] Le repère \(\mathcal{R}_{\theta}=\bigl(O,\overrightarrow{u}(\theta),\overrightarrow{v}(\theta)\bigr)\) s’appelle le repère polaire.
Étant données deux fonctions \(\rho : I \mapsto \mathbb{R}\) et \(\theta : I \mapsto \mathbb{R}\), on peut définir la courbe paramétrée \((I, \overrightarrow{f})\) par \[\boxed{\overrightarrow{F}(t) = \rho(t) \overrightarrow{u}(\theta(t))}\]
(Calcul de la vitesse et de l’accélération dans le repère polaire). \[\boxed{\overrightarrow{F'}(t) = \rho'(t) \overrightarrow{u}\bigl(\theta(t)\bigr) + \rho(t)
\theta'(t)
\overrightarrow{v}\bigl(\theta(t)\bigr)} \quad \textrm{ et} \quad
\boxed{ \overrightarrow{F''}(t) = \bigl[\rho''(t) - \rho(t)\theta'^2(t)\bigr]
\overrightarrow{u}\bigl(\theta(t)\bigr) +
\bigl[2\rho'(t)\theta'(t) + \rho(t)\theta''(t)\bigr]
\overrightarrow{v}\bigl(\theta(t)\bigr)}\]
Il suffit d’appliquer les formules de dérivation usuelles ainsi que les relations \(\dfrac{d\overrightarrow{u}}{d\theta}=\overrightarrow{v}\) et \(\dfrac{d\overrightarrow{v}}{d\theta}=-\overrightarrow{u}\).
Etude d’une courbe \(\rho= f(\theta)\).
r6cm
On considère une courbe polaire \[\rho= f( \theta)\] où \(f : I \mapsto \mathbb{R}\) est une fonction de classe \(\class{k}\), (avec \(k\geqslant 2\)). C’est l’ensemble des points du plan de coordonnées polaires \((\rho,\theta)\) liés par cette relation. Notre but est de tracer une telle courbe.
Une courbe polaire est une courbe paramétrée particulière : \(\overrightarrow{F}(\theta) = \rho(\theta) \overrightarrow{u}(\theta)\), \[\begin{cases} x(\theta) &= \rho(\theta) \cos\theta \\ y(\theta) &= \rho(\theta) \sin\theta \end{cases}\]
Recherche des symétries éventuelles : Il est important, avant de commencer l’étude d’une courbe polaire de réduire l’intervalle d’étude. Quelques exemples :
Si \(\rho(\theta)\) est \(T\) périodique, avec \(T = \dfrac{p}{q} 2\pi\),
Si \(\rho(-\theta) = \pm \rho(\theta)\),
Si \(\rho(\theta_0 - \theta) = \pm \rho(\theta)\).
Etude locale
On exprime \(\overrightarrow{F'}(\theta)\) dans la base \((\overrightarrow{u}(\theta), \overrightarrow{v}(\theta))\) : \[\overrightarrow{F'}(\theta) = \rho'(\theta) \overrightarrow{u} + \rho(\theta) \overrightarrow{v}\]
Les points stationnaires ne peuvent correspondre qu’au passage au pôle. On obtient l’allure locale de la courbe en examinant le signe de \(\rho\) : un point stationnaire pour une courbe polaire ne peut être qu’un point ordinaire (\(\rho\) change de signe) ou un rebroussement de première espèce (\(\rho\) ne change pas de signe) ;
En un point différent de l’origine (donc régulier), si \(V(\theta)\) est l’angle entre la droite \((OM(\theta))\) et la tangente à la courbe en \(M(\theta)\), alors : \[\boxed{ \tan V(\theta) = \dfrac{ \rho(\theta)}{\rho'(\theta)} }\]
Si pour une valeur donnée de \(\theta\), \(\rho'\left(\theta\right)=0\) alors \(\overrightarrow{F'}(\theta)\) est colinéaire à \(\overrightarrow{v}\left(\theta\right)\) et on dit que \(\overrightarrow{F'}(\theta)\) est orthoradial.
Etude des branches infinies :
Elles se produisent lorsque \(\rho(\theta) \xrightarrow[\theta\rightarrow \theta_0]{ } \infty\) ;
Si \(\theta_0 = k\pi\), \((Ox)\) est direction asymptotique. Il suffit d’étudier : \[y(\theta) = \rho(\theta) \sin \theta\]
Si \(\theta_0 = \dfrac{\pi}{2} + k\pi\), il suffit d’étudier : \[x(\theta) = \rho(\theta) \cos\theta\]
Sinon, on fait l’étude dans le repère polaire \((0,\overrightarrow{u}(\theta_0), \overrightarrow{v}(\theta_0))\) : \[Y(\theta) = \rho(\theta) \sin(\theta - \theta_0)\]
Branches infinies spirales :
Si \(\rho(\theta) \xrightarrow[\theta \rightarrow \infty]{ } \infty\) ;
Si \(\rho(\theta) \xrightarrow[\theta \rightarrow \infty]{ } R\), on a un cercle ou un point asymptote ;
La cardioïde
Étudions la cardioïde. Cette courbe est donnée par l’équation polaire \[\rho= a(1+\cos \theta) \quad(a>0) .\] Nous allons nous limiter au cas où \(a=1\), le cas général se traite de manière identique.
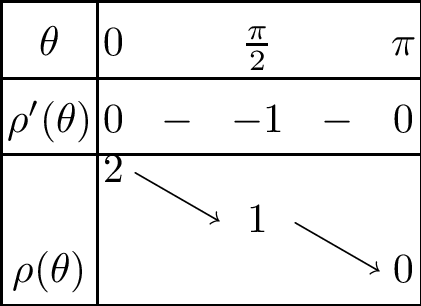
La fonction \(\rho\) est définie sur \(\mathbb{R}\)
Elle est \(2\pi\)-périodique donc il suffit de travailler sur un intervalle de longueur \(2\pi\). Comme \(\rho\) est impaire, on peut étudier la courbe pour \(\theta\in\left[0,\pi\right]\), on déduira la partie manquante par la symétrie d’axe \(\left(Ox\right)\).
Pour tout \(\theta \in\left[0,\pi\right]\), \(\rho'\left(\theta\right)=-\sin \theta\). On en déduit les variations de \(\rho\) :
On remarque que la courbe présente un vecteur tangent orthoradial quand \(\theta=0\).
La courbe présente un point stationnaire en \(\theta=\pi\). Comme \(\rho\) ne change pas de signe en ce point, on a un point de rebroussement de première espèce.
La courbe ne présente pas de branche infinie.
Représentation graphique :
La strophoïde droite
r3cm
(-1.5,-5)(2,5) (0,0)(-1.5,-5)(2,5) t 2 mul cos t cos div t cos mul t 2 mul cos t cos div t sin mul t 2 mul cos t cos div t cos mul t 2 mul cos t cos div t sin mul t 2 mul cos t cos div t cos mul t 2 mul cos t cos div t sin mul (-1,-5)(-1,5) (-1,0)\(-1\)
C’est la courbe polaire d’équation \[\rho= a \dfrac{ \cos 2\theta}{ \cos \theta}\] avec \(a>0\). On se borne à étudier la courbe dans le cas \(a=1\).
La fonction \(\rho\) est définie pour \(\theta\neq \pi/2 ~\left[\pi\right]\).
Il suffit de travailler sur un intervalle de longueur \(2\pi\) car \(\rho\) est \(2\pi\)-périodique. Mais \(\forall \theta \neq \pi/2 ~\left[\pi\right]\), \(\rho\left(\pi-\theta\right)=-\rho\left(\theta\right)\). On peut donc travailler sur un intervalle de longueur \(\pi\). Enfin, comme \(\rho\) est paire, la courbe présente une symétrie d’axe \(\left(Ox\right)\) et il suffit de l’étudier sur \(I=\left[0,\pi/2\right[\).
Pour tout \(\theta\in I\), on montre avec les formules de trigonométrie que \[\rho\left(\theta\right)= \dfrac{ \cos 2\theta}{ \cos \theta}=2\cos \theta - \dfrac{1}{\cos \theta}\] donc \(\rho'\left(\theta\right) = -2\sin\theta -{\scriptstyle\sin\theta\over\scriptstyle\cos^2 \theta}\) qui est négative sur \(I\). On calcule aussi facilement que \(\rho\) ne s’annule qu’en un seul point de \(I\) : \(\pi/4\). On en déduit les variations de \(\rho\) :
On remarque que le vecteur tangent à la courbe en le point de paramètre \(\theta=0\) est orthoradial.
La courbe ne présente pas de point stationnaire.
Par contre, on remarque une branche infinie quand \(\theta \rightarrow \pi/2^-\). Comme : \[x=\rho\left(\theta\right)\cos \theta = \cos \left(2\theta\right) \xrightarrow[\theta\rightarrow \pi/2^-]{}-1 \quad \textrm{ et} \quad y =\rho\left(\theta\right)\sin \theta \xrightarrow[\theta\rightarrow \pi/2^-]{} -\infty,\] on en déduit que la droite \(x=-1\) est asymptote à cette branche infinie. La courbe de plus se trouve à droite de cette asymptote.
On en déduit alors le graphe de la courbe.
Voir les sites web suivants :
http://www.mathcurve.com/courbes2d/courbes2d.shtml
http://perso.wanadoo.fr/jpq/courbes/index.htm
http://turnbull.dcs.st-and.ac.uk/~history/Curves/Curves.html
http://mathworld.wolfram.com/Bibliographie
Barre utilisateur
[ID: 61] [Date de publication: 1 novembre 2021 17:40] [Catégorie(s): Le cours de SUP ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]Commentaires sur le cours
Documents à télécharger
L'article complet