Lecture zen
Géométrie dans l’espace
De la même façon que dans le chapitre consacré à la géométrie plane [geom_plan], ce chapitre a pour vocations de vous familiariser avec le calcul algébrique et de vous donner des représentations pour les objets étudiés dans les chapitres [chapitre_ev] et [chap_dim_ev] d’algèbre linéaire.
Là encore, on pourra passer dans une première lecture les démonstrations qui ne sont pas marquées par un \(\heartsuit\) et se focaliser sur les autres parties.
Préambule
Dans tout ce chapitre on notera \(\mathscr E\) l’ensemble des points de l’espace et \(\mathscr V\) l’ensemble des vecteurs de l’espace. De la même façon que dans le plan, on peut additionner les vecteurs de l’espace ainsi que les multiplier par des scalaires réels. Pour résumer l’ensemble des propriétés de cette addition et de cette multiplication, qui sont les mêmes que pour les vecteurs du plan, on dit que le triplet \((\mathscr V,+,.)\) possède une structure d’espace vectoriel sur \(\mathbb{R}\).
Combinaisons linéaires de vecteurs, droites et plans dans l’espace
(Droite vectorielle, droite affine).
Soit \(\overrightarrow{u}\) un vecteur non nul de l’espace. On appelle droite vectorielle engendrée (ou dirigée) par \(\overrightarrow{u}\) l’ensemble \(D\) des vecteurs de l’espaces colinéaires à \(\overrightarrow{u}\) : \[D=\left\{\overrightarrow{v}\in\mathscr V ~|~ \exists \lambda \in\mathbb{R}: \quad \overrightarrow{v} = \lambda \overrightarrow{u}\right\}\]
Soient \(A\) un point et \(\overrightarrow{u}\) un vecteur de l’espace. La droite affine passant par le point \(A\) et de vecteur directeur \(\overrightarrow{u}\) est l’ensemble \(\mathscr D\) des points \(M\) de l’espace tel que les vecteurs \(\overrightarrow{AM}\) et \(\overrightarrow{u}\) sont colinéaires : \[\mathscr D=\left\{M \in \mathscr E ~|~ \exists \lambda \in\mathbb{R}: \quad \overrightarrow{AM} = \lambda \overrightarrow{u}\right\}\]
Se donnant deux points distincts \(A\) et \(B\) de l’espace, la droite de l’espace passant par les points \(A\) et \(B\) est la droite passant par \(A\) et dirigée par \(\overrightarrow{AB}\).
(Combinaison linéaire de deux vecteurs). Soient \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) trois vecteurs de l’espace. On dit que \(\overrightarrow{w}\) est combinaison linéaire des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) si et seulement si il existe deux réels \(\alpha,\beta\in\mathbb{R}\) tels que \(\overrightarrow{w} = \alpha
\overrightarrow{u}+\beta \overrightarrow{w}\).
(Plan Vectoriel, plan affine ).
Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs non colinéaires de l’espace \(\mathscr V\). On appelle plan vectoriel engendré (ou dirigé) par les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) l’ensemble, noté \(\mathcal P\), des de \(\mathscr V\) qui sont combinaisons linéaires de \(\overrightarrow{u}\) et \(\overrightarrow{v}\) : \[\mathcal P=\left\{\alpha \overrightarrow{u} + \beta \overrightarrow{v} ~|~ \alpha,\beta \in\mathbb{R}\right\}.\]
Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs non colinéaires de l’espace \(\mathscr V\) et \(A\in \mathscr E\) un point de l’espace. On appelle plan affine engendré (ou dirigé) par les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) et passant par \(A\) l’ensemble, noté \(\mathscr P\), des \(M\) de \(\mathscr E\) tels que le vecteur \(\overrightarrow{AM}\) est combinaison linéaire de \(\overrightarrow{u}\) et \(\overrightarrow{v}\) : \[\mathscr P=\left\{M\in \mathscr E ~|~ \exists \left(\alpha,\beta\right) \in\mathbb{R}^2: \quad \overrightarrow{AM}=\alpha \overrightarrow{u} + \beta \overrightarrow{v} \right\}.\]
Avec les notations précédentes : \(M\) est élément du plan affine passant par \(A\) et engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\) si et seulement si le vecteur \(\overrightarrow{AM}\) est élément du plan vectoriel engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\) : \(\mathcal P\).
Le couple \(\left(\overrightarrow{u},\overrightarrow{v}\right)\) forme une base de \(\mathcal P\).
Le triplet \(\left(A,\overrightarrow{u},\overrightarrow{v}\right)\) forme un repère de \(\mathscr P\).
On peut aussi définir un plan affine \(\mathscr P\) en se donnant trois points non alignés \(A\), \(B\) et \(C\) de \(\mathscr E\). On définit le plan affine passant par ces trois points comme étant le plan affine passant par \(A\) et engendré par les vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\).
(Vecteur normal). Un vecteur est dit normal à un plan \(\mathscr P\) si et seulement si il est orthogonal à tous les vecteurs de ce plan.
Se donner un plan vectoriel revient à se donner un vecteur normal à ce plan.
Se donner un plan affine revient à se donner un vecteur normal à ce plan et un point de ce plan.
Vecteurs coplanaires, bases
(Vecteurs coplanaires). Trois vecteurs non nuls sont coplanaires si l’un des trois est élément du plan engendré par les deux autres (ou ce qui est équivalent si l’un de trois est combinaison linéaire des deux autres).
En prenant la négation de ce qui précède: trois vecteurs sont non coplanaires si et seulement si on ne peut écrire aucun des trois comme combinaison linéaire des deux autres (on dit qu’ils sont linéairement indépendants ou qu’ils forment une famille libre).
(Base de l’espace). Un triplet de vecteurs de \(\mathscr V\): \((\overrightarrow{u}, \overrightarrow{v},\overrightarrow{w})\) est une base de \(\mathscr V\) si il est formé de trois vecteurs non coplanaires.
(Coordonnées d’un vecteur dans une base de l’espace). Soit \((\overrightarrow{u}, \overrightarrow{v},\overrightarrow{w})\) une base de \(\mathscr V\). Tout vecteur \(\overrightarrow{x}\) de \(\mathscr V\) s’exprime comme une combinaison linéaire unique des \(3\) vecteurs \(\overrightarrow{u}, \overrightarrow{v}\) et \(\overrightarrow{w}\) c’est-à-dire : \[\forall x\in\mathscr V,\quad \exists ! (\alpha,\beta,\gamma)\in\mathbb{R}^3:\quad \overrightarrow{x}=\alpha\overrightarrow{u}+\beta \overrightarrow{v}+\gamma \overrightarrow{w}\] Le triplet \((\alpha,\beta,\gamma)\) est appelé coordonnées de \(\overrightarrow{x}\) dans la base \(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w})\). On notera : \[\overrightarrow{x} \left|\begin{matrix} \alpha \\ \beta \end{matrix} \right.{\gamma} \textrm{ ou } \overrightarrow{x} \left(\begin{matrix} \alpha \newline \beta \end{matrix} \right){\gamma} \textrm{ ou aussi } \overrightarrow{x}(\alpha,\beta,\gamma)\]
Soit \(\mathscr P\) le plan engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\). Soit \(\overrightarrow{m_0}\) le projeté du vecteur \(\overrightarrow{m}\) sur \(\mathscr P\) parallèlement à \(\overrightarrow{w}\). Il existe \(\gamma \in \mathbb{R}\) tel que \(\overrightarrow{m}=\overrightarrow{m_0}+\gamma \overrightarrow{w}\). Comme \(\overrightarrow{m_0}\) est élément du plan engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\), il existe \((\alpha,\beta)\in\mathbb{R}^2\) tel que \(\overrightarrow{m_0}=\alpha \overrightarrow{u}+\beta \overrightarrow{v}\). Donc \(\overrightarrow{m}= \alpha\overrightarrow{u}+\beta \overrightarrow{v}+\gamma \overrightarrow{w}\).
Ce triplet est unique: Si il existe un autre triplet \((\alpha',\beta',\gamma')\in\mathbb{R}^3\) vérifiant \(\overrightarrow{m}=\alpha'\overrightarrow{u}+\beta' \overrightarrow{v}+\gamma' \overrightarrow{w}\) alors \((\alpha-\alpha')\overrightarrow{u}+(\beta-\beta') \overrightarrow{v}+(\gamma-\gamma') \overrightarrow{w}=\overrightarrow{0}\). Supposons qu’un des trois: \(\alpha-\alpha'\), \(\beta-\beta'\), \(\gamma-\gamma'\) ne soit pas nul, par exemple \(\alpha-\alpha'\), alors \[\overrightarrow{u}={\scriptstyle\beta-\beta'\over\scriptstyle\alpha-\alpha'}\overrightarrow{v}+{\scriptstyle\gamma-\gamma'\over\scriptstyle\alpha-\alpha'}\overrightarrow{w}\] et \(\overrightarrow{u}\) est combinaison linéaire de \(\overrightarrow{v}\) et \(\overrightarrow{w}\), et est donc élément du plan engendré par ces deux vecteurs, ce qui est contradictoire avec notre hypothèse de départ. Le triplet \((\alpha,\beta,\gamma)\) est donc unique.
(Base orthogonale, orthonormale). Soit \(\mathscr B(\overrightarrow{u}, \overrightarrow{v},\overrightarrow{w})\) une base de \(\mathscr V\). Si les vecteurs \(\overrightarrow{u}, \overrightarrow{v},\overrightarrow{w}\) sont deux à deux orthogonaux, on dit que la base \(\mathscr B\) est orthogonale. Si ils sont de plus unitaires, on dit que \(\mathscr B\) est orthonormale.
Orientation de l’espace, base orthonormale directe
Comme on l’a vu dans le chapitre [geom_plan], il est important, pour pouvoir définir certaines notions ou résoudre certains problèmes, de savoir orienter l’angle formé par deux vecteurs donnés. Dans le cas du plan, il est facile de fixer cette orientation. Il suffit de décider, entre le sens horaire et le sens trigonométrique, quel sera le sens positif. Dans le cas de l’espace, les choses sont plus compliquées. Considérons deux vecteurs \(\overrightarrow{i}\) et \(\overrightarrow{j}\) de l’espace non colinéaires et nommons \(\mathcal P\) le plan vectoriel qu’ils engendrent. Ce plan sépare l’espace en deux demi espaces \(\mathcal E_1\) et \(\mathcal E_2\). Supposons que chacune de ces deux parties contient un observateur du plan \(\mathcal P\) nommé \(\mathcal O_1\) pour \(\mathcal E_1\) et \(\mathcal O_2\) pour \(\mathcal E_2\). Chacun de ces deux observateurs peut orienter le plan \(\mathscr P\) mais le sens trigonométrique pour \(\mathcal O_1\) correspond au sens horaire pour \(\mathcal O_2\) et le sens horaire pour \(\mathcal O_1\) correspond au sens trigonométrique pour \(\mathcal O_2\). L’orientation d’un plan dans l’espace dépend donc de la position d’où on l’observe. Nous allons tout d’abord expliquer ce que signifie orienter l’espace puis nous en tirerons un procédé permettant d’orienter les plans de l’espace.
Il existe plusieurs règles mnémotechniques pour fixer une orientation de l’espace. Parmi celles ci, donnons celle dite du bonhomme d’ampère .
Considérons \((O,\overrightarrow{i},\overrightarrow{j}){k}\) un repère orthonormal de l’espace. Soient \(I\), \(J\) et \(K\) des points de \(\mathscr E\) tels que \(\overrightarrow{OI}=\overrightarrow{i}\), \(\overrightarrow{OJ}=\overrightarrow{j}\) , \(\overrightarrow{OK}=\overrightarrow{k}\). On considère un observateur placé les pieds en \(O\), la tête en \(K\) et qui a le point \(I\) devant lui.
Par convention, on dit que :
le repère \((O,\overrightarrow{i},\overrightarrow{j}){k}\) est direct si l’observateur a le point \(J\) à sa gauche. On dit aussi que la base \((\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})\) est directe.
le repère \((O,\overrightarrow{i},\overrightarrow{j}){k}\) est indirect si l’observateur a le point \(J\) à sa droite. On dit aussi que la base \((\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k})\) est indirecte.
Choisir une orientation de l’espace, c’est choisir de travailler avec les repères directs, ou avec les repères indirects. Si on fixe un repère dans l’espace, on choisit une orientation.
Considérant une base de l’espace \({\mathscr B}\):
Si on échange deux vecteurs de \({\mathscr B}\), on change l’orientation de \({\mathscr B}\).
Si on échange un des vecteurs de \({\mathscr B}\) avec son opposé, on change l’orientation de \({\mathscr B}\).
Si on effectue une permutation circulaire sur les éléments de \({\mathscr B}\) on ne change pas son orientation.
(Orientation d’un plan dans l’espace). Étant donnés un plan \(\mathscr P\) et un vecteur normal \(\overrightarrow{n}\) à ce plan, il existe une unique orientation du plan \(\mathscr P\) telle que pour toute base orthonormale directe \((\overrightarrow{u}, \overrightarrow{v})\) de ce plan, le triplet \(\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{n}\right)\) forme une base orthonormale directe de \(\mathscr E\). On dit que le plan \(\mathscr P\) est orienté par \(\overrightarrow{n}\).
Mode de repérage dans l’espace, coordonnées cartésiennes
Coordonnées cartésiennes
Définitions
(Repère de l’espace). On dit que le quadruplet \(\mathscr R\left(O, \overrightarrow{u}, \overrightarrow{v}, \overrightarrow{w}\right)\in\mathscr E
\times \mathscr{V}^3\) est un repère de l’espace \(\mathscr E\) si et seulement si \(\left(\overrightarrow{u}, \overrightarrow{v}, \overrightarrow{w}\right)\) est une base de \(\mathscr V\). \(O\) est appelé origine du repère \(\mathscr R\).
Le repère \(\mathscr R\) est dit orthogonal si et seulement si la base \(\left(\overrightarrow{u}, \overrightarrow{v}, \overrightarrow{w}\right)\) est orthogonale.
Le repère \(\mathscr R\) est dit orthonormal si et seulement si la base \(\left(\overrightarrow{u}, \overrightarrow{v}, \overrightarrow{w}\right)\) est orthonormale.
(Coordonnées d’un point dans un repère cartésien).
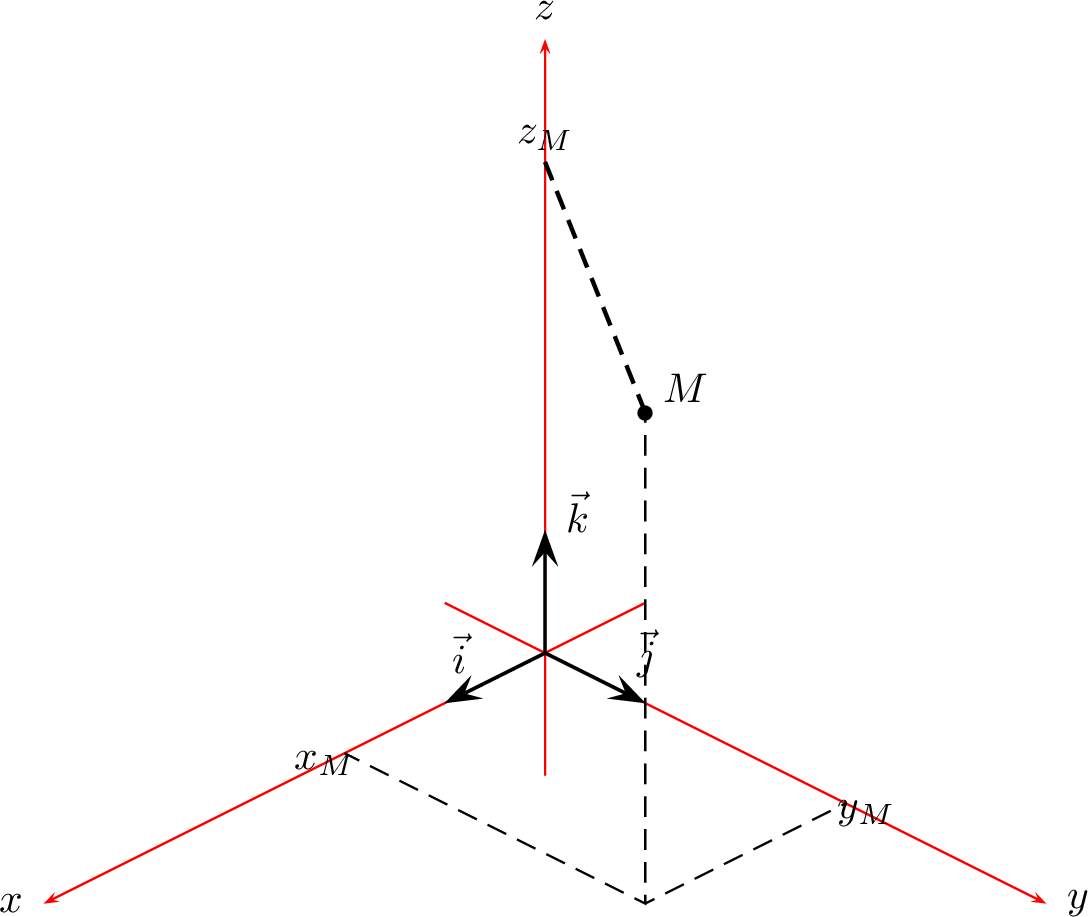
Soit \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère cartésien de l’espace. Soit \(M\in\mathscr E\) un point de l’espace. Il existe un unique triplet \(\left(\alpha,\beta,\gamma\right)\in\mathbb{R}^3\) tel que \(\overrightarrow{OM}=\alpha \overrightarrow{i} + \beta \overrightarrow{j} +
\gamma \overrightarrow{k}\). Ce triplet s’appelle les coordonnées de \(M\) dans le repère \(\mathscr R\). On le note : \[M \left|\begin{matrix} \alpha \\ \beta \end{matrix} \right.{\gamma} \textrm{ ou }
M \left(\begin{matrix} \alpha \newline \beta \end{matrix} \right){\gamma} \textrm{ ou aussi } M(\alpha,\beta,\gamma)\]
C’est une conséquence directe de la proposition [coord_vecteur_base_espace]
La donnée d’un repère \(\mathscr R\) de \(\mathscr E\) permet de construire l’application : \[\theta: \left\{ \begin{array}{ccl} \mathscr E & \longrightarrow & \mathbb{R}^3 \\ M & \longmapsto & \left|\begin{matrix} \alpha \newline \beta \end{matrix} \right.{\gamma} \end{array} \right.\] où \(\left(\alpha,\beta,\gamma\right)\) sont les coordonnées de \(M\) dans \(\mathscr R\). Cette application est bijective et permet d’identifier \(\mathscr E\) et \(\mathbb{R}^3\). De même, on peut identifier \(\mathscr V\) et \(\mathbb{R}^3\).
Calcul algébrique avec les coordonnées
(Calculs avec les coordonnées). Soit \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère cartésien de l’espace. Soient \(\overrightarrow{u}\) et \(\overrightarrow{u'}\) des vecteurs de coordonnées, dans \(\mathscr R\) : \[\overrightarrow{u} \left|\begin{matrix} x \\ y \end{matrix} \right.{z} \quad \textrm{ et} \quad\overrightarrow{u'} \left|\begin{matrix} x' \\ y' \end{matrix} \right.{z'}\] Soient \(\alpha,\alpha'\in\mathbb{R}\). Les coordonnées du vecteur \(\alpha \overrightarrow{u} + \beta
\overrightarrow{u'}\) sont : \[\boxed{\alpha \overrightarrow{u} + \beta \overrightarrow{u'} \left|\begin{matrix} \alpha x + \beta x' \newline \alpha
y + \alpha' y' \end{matrix} \right.{\alpha z + \alpha' z'}}\]
(1). Par définition, on a : \(\overrightarrow{u}=x \overrightarrow{i} + y \overrightarrow{j} + z \overrightarrow{k}\) et \(\overrightarrow{u'}=x' \overrightarrow{i}
+ y' \overrightarrow{j} + z' \overrightarrow{k}\). Par conséquent : \[\alpha \overrightarrow{u} + \beta \overrightarrow{u'}=\left(\alpha x + \beta x'\right)\overrightarrow{i} + \left(\alpha y +
\alpha' y'\right)\overrightarrow{j} + \left(\alpha z + \alpha' z'\right)\overrightarrow{k}\] ce qui prouve le résultat.
Norme d’un vecteur, distance entre deux points dans un repère orthonormé
(Norme d’un vecteur). Soit \(\overrightarrow{u}\) un vecteur de \(\mathscr V\) possédant \(\overrightarrow{AB}\) comme représentant dans \(\mathscr V\) où \(A,B\in\mathscr E\). On appelle norme de \(\overrightarrow{u}\) et on note \(\left\|\overrightarrow{u}\right\|\) la longueur \(AB\).
(Expression de la norme d’un vecteur dans un repère orthonormal). Soit \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère orthonormal de l’espace et \(\overrightarrow{u}\) un vecteur de coordonnées \(\overrightarrow{u} \left(x,y,z\right)\) dans la base associée à ce repère. On a : \[\boxed{\left\|\overrightarrow{u}\right\| =\sqrt{x^2 + y^2 + z^2}}\]
(1). Soit \(M\in \mathscr E\) tel que \(\overrightarrow{OM}=\overrightarrow{u}\). Soient :
\(H\) le projeté orthogonal de \(M\) sur le plan horizontal : \(\left(O,\overrightarrow{i}, \overrightarrow{j}\right)\).
\(I\) le point de \(\left(Ox\right)\) donné par : \(\overrightarrow{OI}=x\overrightarrow{i}\).
\(J\) le point de \(\left(Oy\right)\) donné par : \(\overrightarrow{OI}=y\overrightarrow{j}\).
Soient \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère orthonormal de l’espace, \(A\left(x_A,y_A,z_A\right)\) et \(B\left(x_B,y_B,z_B\right)\) des points de l’espace alors \[\boxed{AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2+\left(z_B-z_A\right)^2}}\]
(1). Les coordonnées du vecteur \(\overrightarrow{AB}\) sont \[\overrightarrow{AB} \left|\begin{matrix} x_B-x_A \newline y_B-y_A \end{matrix} \right.{z_B-z_A}\] Si on applique à ce vecteur la formule précédente, on obtient le résultat escompté.
Coordonnées cylindriques et sphériques
Coordonnées cylindriques
Coordonnées sphériques
Multimédia: Animation: on déplace un point dans l’espace et on représente géométriquement ses coordonnées cartésiennes et sphériques/cylindriques
(Système de coordonnées cylindriques). Soient :
\(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère orthonormal de l’espace
\(M \left|\begin{matrix} x \newline y \end{matrix} \right.{z}\) un point de \(\mathscr E\).
\(P\) le projeté orthogonal de \(M\) sur le plan \(\left(Oxy\right)\) muni du repère orthonormal \(\mathscr R_0\left(P,\overrightarrow{i},\overrightarrow{j}\right)\).
On appelle système de coordonnées cylindriques de \(M\) par rapport à \(\mathscr R\) tout triplet de réels \(\left(r,\theta,z\right)\) tel que \[\overrightarrow{OM}=r \overrightarrow{u}\left(\theta\right)+z\overrightarrow{k}\] où :
\(\left(r,\theta\right)\) est un système de coordonnées polaires pour \(P\) relativement à \(\mathscr R_0\).
\(\theta\) est une mesure de l’angle \(\left(\widehat{\overrightarrow{i},\overrightarrow{OP}}\right)\).
\(\overrightarrow{u}\left(\theta\right)\) est le vecteur \(\overrightarrow{u}\left(\theta\right)=\cos \theta \overrightarrow{i} + \sin \theta \overrightarrow{j}\)
\(r\) est le réel positif tel que \(\overrightarrow{OP}=r\overrightarrow{u}\left(\theta\right)\)
\(z\) est la cote de \(M\) dans \(\mathscr R\).
(Lien entre les coordonnées cylindriques et les coordonnées cartésiennes). Soit \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère orthonormal de l’espace, \(M\) un point de l’espace de coordonnées cartésiennes \(\left(x,y,z\right)\) dans \(\mathscr
R\) et de coordonnées cylindriques par rapport à \(\mathscr R\) \(\left(r,\theta,z\right)\). On a : \[\boxed{\begin{cases}
x=r\cos \theta \\ y= r\sin \theta \newline z=z
\end{cases}}\]
(1). Soit \(M\) un point de l’espace de coordonnées cartésiennes \(\left(x,y,z\right)\) dans \(\mathscr R\). Soit \(P\) le projeté orthogonal de \(M\) sur le plan horizontal \(\left(O,\overrightarrow{i}, \overrightarrow{j}\right)\) et \(\left(\rho,\theta\right)\) un système de coordonnées polaires pour \(P\) par rapport au repère orthonormal direct \(\mathscr R_0 \left(O,\overrightarrow{i},\overrightarrow{j}\right)\). Avec \(\overrightarrow{u}\left(\theta\right)=\cos \theta \overrightarrow{i} + \sin \theta \overrightarrow{j}\), on a \(\overrightarrow{OP}=\rho \overrightarrow{u}\left(\theta\right)\) et : \[\begin{aligned}
\overrightarrow{OM}&=& \overrightarrow{OP}+\overrightarrow{PM}\\
&=& r\overrightarrow{u}\left(\theta\right)+z \overrightarrow{k}\newline
&=& r\cos \theta \overrightarrow{i} + r\sin\theta \overrightarrow{j} + z\overrightarrow{k}\end{aligned}\] d’où le résultat.
Coordonnées sphériques
(Système de coordonnées sphériques). Soient \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère orthonormal de l’espace, \(M\) un point de l’espace et \(P\) son projeté orthogonal sur le plan horizontal \(\left(O,\overrightarrow{i}, \overrightarrow{j}\right)\).
On appelle système de coordonnées sphériques de \(M\) par rapport à \(\mathscr R\) tout triplet de réels \(\left(r,\theta,\varphi\right)\) tel que :
\(r=\left\|\overrightarrow{OM}\right\|\).
\(\left(\rho,\theta\right)\) est un système de coordonnées polaires de \(P\) par rapport au repère orthonormal direct \(\left(O,\overrightarrow{i},\overrightarrow{j}\right)\).
\(\varphi\) est la mesure de l’angle \(\left(\widehat{\overrightarrow{k},\overrightarrow{OM}}\right)\) élément de \(\left[0,\pi\right]\).
\(\theta\) étant une mesure de l’angle orienté \(\left(\widehat{\overrightarrow{i},\overrightarrow{OP}}\right)\), il est défini modulo \(2\pi\).
L’angle \(\left(\overrightarrow{k},\overrightarrow{OM}\right)\) n’est pas orienté car on n’a pas choisi d’orientation du plan \(\left(zOM\right)\). C’est pour cela que sa mesure est donnée modulo \(\pi\).
On utilise parfois la latitude : \({\scriptstyle\pi\over\scriptstyle 2}-\varphi\) à la place de la colatitude.
(Lien entre les coordonnées sphériques et les coordonnées cartésiennes). Soient \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère orthonormal de l’espace, \(M\) un point de l’espace de coordonnées cartésiennes \(\left(x,y,z\right)\) dans \(\mathscr
R\) et de coordonnées sphériques \(\left(r,\theta,\varphi\right)\). On a : \[\boxed{\begin{cases}
x=r\sin \varphi \cos \theta\\ y= r\sin \varphi\sin\theta \newline z=r\cos \varphi
\end{cases}}\]
(1). Soit \(M\) un point de l’espace de coordonnées cartésiennes \(\left(x,y,z\right)\) dans \(\mathscr R\) et soit \(P\) le projeté orthogonal de \(M\) sur le plan horizontal \(\left(O,\overrightarrow{i}, \overrightarrow{j}\right)\). Soit \(\left(\rho,\theta\right)\) un système de coordonnées polaires pour \(P\) par rapport au repère orthonormal direct \(\mathscr R_0 \left(O,\overrightarrow{i},\overrightarrow{j}\right)\) et : \(\overrightarrow{u}\left(\theta\right)=\cos \theta \overrightarrow{i} + \sin \theta \overrightarrow{j}\). On a : \(\overrightarrow{OP}=\rho \overrightarrow{u}\left(\theta\right)\) et : \[\begin{aligned}
\overrightarrow{OM}&=& r\cos \varphi \overrightarrow{k} + r\sin\varphi \overrightarrow{u}\left(\theta\right)\newline
&=& r\cos \varphi \overrightarrow{k} + r\sin\varphi \cos \theta \overrightarrow{i} + r\sin \varphi
\sin\theta \overrightarrow{j}\end{aligned}\] d’où le résultat.
Si à la place de désigner la colatitude, \(\varphi\) désigne la latitude alors les formules précédentes deviennent : \[\begin{cases}
x=r\cos \varphi \cos \theta\\ y= r\cos \varphi\sin\theta \newline z=r\sin \varphi
\end{cases}.\]
Produit scalaire
Définition
(Produit scalaire). Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs de \(\mathscr V\). Soient \(O\), \(A\), \(B\) trois points de \(\mathscr E\) tel que : \(\overrightarrow{OA}=\overrightarrow{u}\) et \(\overrightarrow{OB}=\overrightarrow{v}\) et \(\mathscr P\) la plan contenant ces \(3\) points. On appelle produit scalaire de \(\overrightarrow{u}\) et \(\overrightarrow{v}\) leur produit scalaire dans le plan \(\mathscr P\). En particulier, si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont non nuls, on a \[\overrightarrow{u} . \overrightarrow{v} = \left(\overrightarrow{u},\overrightarrow{v}\right)=\left\|\overrightarrow{u}\right\|.\left\|\overrightarrow{v}\right\|.\cos \theta\] où \(\theta\) est une mesure de l’angle \(\left(\overrightarrow{OA},\overrightarrow{OB}\right)\) dans le plan \(\mathscr P\).
Cette définition ne nécessite pas de définir une orientation dans la plan \(\mathscr P\) et l’angle \(\theta=\left(\overrightarrow{OA},\overrightarrow{OB}\right)\) ne doit pas nécessairement être orienté. En effet, si on change l’orientation du plan, l’angle \(\theta\) est changé en son opposé ce qui laisse invariant son cosinus.
\(\left\|\overrightarrow{u}\right\|^2 = \overrightarrow{u} . \overrightarrow{u}\).
Deux vecteurs non nuls de \(\mathscr V\) sont orthogonaux si et seulement si leur produit scalaire est nul.
(1). C’est une conséquence de la même propriété mais dans le plan.
Expression dans une base orthonormale
Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs de \(\mathscr V\) alors \[\overrightarrow{u} . \overrightarrow{v} = {\scriptstyle 1\over\scriptstyle 2}\left(\left\|\overrightarrow{u} + \overrightarrow{v}\right\|^2 - \left\|\overrightarrow{u}\right\|^2 -
\left\|\overrightarrow{v}\right\|^2 \right)\]
Soit \(\mathscr P\) le plan vectoriel engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\). Le vecteur \(\overrightarrow{u}+\overrightarrow{v}\) est élément de \(\mathscr P\). Les propriétés du produit scalaire dans le plan permettent d’écrire \[\left\|\overrightarrow{u}+\overrightarrow{v}\right\|^2 = \left\|\overrightarrow{u}\right\|^2 + \left\|\overrightarrow{v}\right\|^2 +2 \overrightarrow{u} . \overrightarrow{v}.\] Le produit scalaire des deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) dans l’espace coïncide avec celui dans le plan \(\mathscr P\). On obtient donc la formule annoncée.
(Expression du produit scalaire dans une base orthonormale). Soient \(\mathscr R\left(O, \overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) un repère orthonormal de l’espace, \(\left(x,y,z\right)\) et \(\left(x',y',z'\right)\) les coordonnées respectives des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de \(\mathscr V\) dans \(\mathscr R\). On a \[\boxed{\overrightarrow{u} . \overrightarrow{v} = xx'+yy'+zz'}\]
(1). On a \(\left\|\overrightarrow{u}\right\|^2=x^2+y^2+z^2\) et \(\left\|\overrightarrow{v}\right\|^2=x'^2+y'^2+z'^2\). Par ailleurs \[\begin{aligned}
\left\|\overrightarrow{u}+\overrightarrow{v} \right\|^2&=&\left(x+x'\right)^2+\left(y+y'\right)^2+\left(z+z'\right)^2\newline
&=& x^2+2xx'+x'^2 + y^2+2yy'+y'^2 + z^2+2zz'+z'^2 .\end{aligned}\] Par application de la formule établie dans le lemme précédent, on obtient l’expression mentionnée pour le produit scalaire.
Propriétés du produit scalaire
(Symétrie du produit scalaire). [] Le produit scalaire est symétrique: si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs de \(\mathscr V\) alors: \[\boxed{\overrightarrow{u} . \overrightarrow{v} = \overrightarrow{v} . \overrightarrow{u}}\]
C’est clair en passant en coordonnées. On peut aussi voir cette proposition comme une conséquence directe du fait que le produit scalaire dans le plan est symétrique, voir proposition [prop_prod_scal_plan_sym] page [prop_prod_scal_plan_sym].
(Bilinéarité du produit scalaire). [] Le produit scalaire est bilinéaire. Ce qui signifie que pour tous vecteurs \(\overrightarrow{u}\), \(\overrightarrow{u_1}\), \(\overrightarrow{u_2}\), \(\overrightarrow{v}\), \(\overrightarrow{v_1}\), \(\overrightarrow{v_2}\) de \(\mathscr V\) et pour tous réels \(\lambda_1\), \(\lambda_2\) \[\boxed{\overrightarrow{u} .(\lambda_1 \overrightarrow{v_1}+\lambda_2 \overrightarrow{v_2})=\lambda_1\overrightarrow{u} .\overrightarrow{v_1}+\lambda_2\overrightarrow{u} .\overrightarrow{v_2}} \quad \textrm{ et} \quad
\boxed{(\lambda_1 \overrightarrow{u_1}+\lambda_2 \overrightarrow{u_2}).\overrightarrow{v}=\lambda_1\overrightarrow{u_1} .\overrightarrow{v}+\lambda_2\overrightarrow{u_2} .\overrightarrow{v}}\]
C’est clair en passant en coordonnées.
Soit \(\mathscr B\left(\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}\right)\) une base orthonormale. Soit \(\overrightarrow{u}\) un vecteur de \(\mathscr V\) de coordonnées \(\left(x,y,z\right)\) dans \(\mathscr B\). Alors \[\boxed{x=\overrightarrow{u} . \overrightarrow{i} \quad y=\overrightarrow{u} . \overrightarrow{j} \quad z=\overrightarrow{u} . \overrightarrow{k}}\]
Laissée en exercice...
Produit vectoriel
Définition du produit vectoriel
(Produit vectoriel). On suppose qu’on a choisi une orientation de l’espace. Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) deux vecteurs de \(\mathscr V\). Soient \(\mathscr P\) un plan de l’espace contenant ces deux vecteurs et \(\overrightarrow{k}\) un vecteur normal unitaire à \(\mathscr P\). Fixant \(\overrightarrow{k}\), on fixe une orientation de \(\mathscr P\). On appelle produit vectoriel de \(\overrightarrow{u}\) et \(\overrightarrow{v}\) le vecteur, noté \(\overrightarrow{u} \wedge \overrightarrow{v}\) ou \(\overrightarrow{u} \times \overrightarrow{v}\), donné par \[\overrightarrow{u} \wedge \overrightarrow{v}=\mathop{\rm det}(\overrightarrow{u},\overrightarrow{v}) \overrightarrow{k}.\]
Il y a deux choix possibles pour un vecteur normal unitaire à \(\mathscr P\): \(\overrightarrow{k}\) ou \(-\overrightarrow{k}\). Le produit vectoriel dépend donc à priori du choix fait au départ pour ce vecteur normal.
En choisissant le vecteur \(-\overrightarrow{k}\) à la place du vecteur \(\overrightarrow{k}\), on change l’orientation de \(\mathscr P\), et donc le signe de l’angle orienté \((\widehat{\overrightarrow{u},
\overrightarrow{v}})\) ainsi que le signe du déterminant du couple \((\overrightarrow{u},\overrightarrow{v})\). Mais ce changement de signe est compensé par le changement du vecteur \(\overrightarrow{k}\) en le vecteur \(-\overrightarrow{k}\) : \((\overrightarrow{u} \wedge_{\overrightarrow{k}} \overrightarrow{v})=\mathop{\rm det}_{\overrightarrow{k}}(\overrightarrow{u},\overrightarrow{v}) \overrightarrow{k} = - \mathop{\rm det}_{-\overrightarrow{k}}(\overrightarrow{u},\overrightarrow{v}) (-\overrightarrow{k})=(\overrightarrow{u} \wedge_{-\overrightarrow{k}} \overrightarrow{v}).\)
Notons \((\overrightarrow{u} \wedge_{\overrightarrow{k}} \overrightarrow{v})\) le produit vectoriel construit en ayant choisi le vecteur \(\overrightarrow{k}\) et \((\overrightarrow{u} \wedge_{-\overrightarrow{k}} \overrightarrow{v})\) le produit vectoriel construit en ayant choisi le vecteur \(-\overrightarrow{k}\). Notons aussi \(\mathop{\rm det}_{\overrightarrow{k}}(\overrightarrow{u},\overrightarrow{v})\) le déterminant des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) dans le plan \(\mathscr P\) orienté par \(\overrightarrow{k}\) et \(\mathop{\rm det}_{-\overrightarrow{k}}(\overrightarrow{u},\overrightarrow{v})\) le déterminant des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) dans le plan \(\mathscr P\) orienté par \(-\overrightarrow{k}\) .
(Norme du produit vectoriel de deux vecteurs).
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs de \(\mathscr V\): \[\boxed{\left\| \overrightarrow{u}
\wedge \overrightarrow{v} \right\| = |\mathop{\rm det}(\overrightarrow{u},\overrightarrow{v})| = \left\|\overrightarrow{u}\right\|.\left\|\overrightarrow{v}\right\|.\left|\sin(\widehat{\overrightarrow{u}, \overrightarrow{v}})\right|}\]
En utilisant la définition du déterminant de deux vecteurs dans le plan et si \(\overrightarrow{n}\) est un vecteur normal unitaire à un plan vectoriel contenant \(\overrightarrow{u}\) et \(\overrightarrow{v}\), on obtient : \[\left\| \overrightarrow{u}
\wedge \overrightarrow{v} \right\| =\left\| \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v}\right) \overrightarrow{n} \right\| = \left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v}\right)\right|\left\|\overrightarrow{n}\right\|= \left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v}\right)\right|= \left\|\overrightarrow{u}\right\|.\left\|\overrightarrow{v}\right\|.\left|\sin(\widehat{\overrightarrow{u}, \overrightarrow{v}})\right|.\]
\(|\sin(\widehat{\overrightarrow{u}, \overrightarrow{v}})|\) ne dépend pas de l’orientation choisie pour le plan \(\mathscr P\) contenant les deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
\(|| \overrightarrow{u} \wedge \overrightarrow{v} ||\) est l’aire du parallélogramme construit à partir des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
(Caractérisation de la colinéarité de deux vecteurs via le produit vectoriel). Deux vecteurs de \(\mathscr V\) sont colinéaires si et seulement si leur produit vectoriel est nul.
Considérons un plan \(\mathcal P\) contenant ces deux vecteurs. Ces deux vecteurs sont colinéaires si et seulement si leur déterminant dans le plan \(\mathscr P\) est nul.
Soient \(\overrightarrow{i}\) et \(\overrightarrow{j}\) deux vecteurs orthogonaux (respectivement orthogonaux et unitaires) de \(\mathscr V\). Alors \((\overrightarrow{i},\overrightarrow{j},\overrightarrow{i}\wedge \overrightarrow{j})\) forme une base orthogonale (respectivement orthonormale) directe de l’espace.
La droite passant par le point \(A\) et de vecteur directeur \(\overrightarrow{u}\) est l’ensemble des points \(M\) du plan vérifiant \[\overrightarrow{AM}\wedge \overrightarrow{u}=\overrightarrow{0}.\]
Interprétation géométrique du produit vectoriel
Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) des vecteurs de \(\mathscr V\) et \(\overrightarrow{w}= \overrightarrow{u} \wedge \overrightarrow{v}\). On obtient \(\overrightarrow{w}\) à partir de \(\overrightarrow{u}\) et \(\overrightarrow{v}\) en composant:
La projection sur un plan \(\mathscr P\) orthogonal à \(\overrightarrow{u}\). L’image de \(\overrightarrow{v}\) par cette projection est un vecteur \(\overrightarrow{v_1}\) de norme \(||\overrightarrow{v} || \,|\sin ({\overrightarrow{u},\overrightarrow{v}})|\). (Remarquons que cette dernière expression est indépendante de l’orientation de l’espace choisie).
La rotation d’angle \({\scriptstyle\pi\over\scriptstyle 2}\) dans le plan \(\mathscr P\) orienté par le vecteur normal \(\overrightarrow{u}\) qui transforme le vecteur \(\overrightarrow{v_1}\) en un vecteur \(\overrightarrow{v_2}\) de même norme que \(\overrightarrow{v_1}\) et directement orthogonal à \(\overrightarrow{u}\) et \(\overrightarrow{v}\)
L’homothétie de rapport \(||\overrightarrow{u}||\) qui transforme \(\overrightarrow{v_2}\) en un vecteur \(\overrightarrow{v_3}\) de norme \(||\overrightarrow{u} ||\,||\overrightarrow{v}|| \,|\sin ({\overrightarrow{u},\overrightarrow{v}})|\) directement orthogonal à \(\overrightarrow{u}\) et \(\overrightarrow{v}\). \(\overrightarrow{v_3}\) est donc par définition égal à \(\overrightarrow{u} \wedge \overrightarrow{v}\).
Propriétés du produit vectoriel
(Le produit vectoriel est antisymétrique).
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont éléments de \(\mathscr V\) alors \[\boxed{\overrightarrow{v} \wedge \overrightarrow{u}= - \overrightarrow{u} \wedge \overrightarrow{v}}\]
C’est une conséquence directe de l’antisymétrie du déterminant de deux vecteurs dans le plan.
Interlude
Lors d’une première lecture, on pourra passer directement à la proposition [bilinearite_produit_vect] page [bilinearite_produit_vect]. Ce qui suit permet de démontrer cette proposition mais n’est pas important pour la compréhension du chapitre.
(Application linéaire dans l’espace). Soit \(f:\mathscr V\longrightarrow \mathscr V\). On dit que \(f\) est linéaire si pour tout couple \((\overrightarrow{u}, \overrightarrow{v})\) de \(\mathscr V^2\) et tout réel \(\lambda\), \[f(\overrightarrow{u}+\overrightarrow{v})=f(\overrightarrow{u})+ f ( \overrightarrow{v} ) \quad \textrm{ et} \quad f(\lambda \overrightarrow{u})=\lambda f(\overrightarrow{u}).\]
(Caractérisation des applications linéaires). Soit \(f:\mathscr V\longrightarrow \mathscr V\). \(f\) est linéaire si et seulement si, pour tout couple \((\overrightarrow{u}, \overrightarrow{v})\) de \(\mathscr V^2\) et pour tout couple de réels \((\alpha,\beta)\) \[\boxed{ f(\alpha\overrightarrow{u} + \beta\overrightarrow{v})=\alpha f(\overrightarrow{u})+\beta f(\overrightarrow{v}) }.\]
Laissée en exercice.
Une application composée de deux applications linéaires est encore linéaire.
Laissée en exercice.
(Application bilinéaire). Une application \(f:\mathscr V\times \mathscr V\longrightarrow \mathscr V\) est dite bilinéaire si elle est linéaire en chacune de ses variables, ce qui signifie que pour tout vecteurs \(\overrightarrow{u}, ~ \overrightarrow{v}\) de \(\mathscr V\) :
si on fixe \(\overrightarrow{u}\): \(f(\overrightarrow{u},.): \left\{ \begin{array}{ccl} \mathscr V & \longrightarrow & \mathscr V \\ \overrightarrow{v} & \longmapsto & f(\overrightarrow{u}, \overrightarrow{v}) \end{array} \right.\) est linéaire.
si on fixe \(\overrightarrow{v}\): \(f(.,\overrightarrow{v}): \left\{ \begin{array}{ccl} \mathscr V & \longrightarrow & \mathscr V \newline \overrightarrow{u} & \longmapsto & f(\overrightarrow{u}, \overrightarrow{v}) \end{array} \right.\) est linéaire.
Quelques exemples d’applications linéaires fort utiles pour ce qui vient...
Soit \(\overrightarrow{u}\) un vecteur de \(\mathscr V\). Soient \((O,\overrightarrow{i},\overrightarrow{j}){k}\) une base orthonormale directe telle que \(\overrightarrow{i}\) et \(\overrightarrow{u}\) sont colinéaires et telle que \((\overrightarrow{j},\overrightarrow{k})\) est une base du plan orthogonale à \(\overrightarrow{u}\).
La projection orthogonale \(p\) sur le plan orthogonale à \(\overrightarrow{u}\) est linéaire.
Soient \(\overrightarrow{v}\) et \(\overrightarrow{v}'\) deux vecteurs de \(\mathscr V\) de coordonnées respectives \((x,y,z)\) et \((x',y',z')\) dans \((\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) alors \(p(\overrightarrow{v})\) est le vecteur de coordonnées \((0,y,z)\) et \(p(\overrightarrow{v'})\) est le vecteur de coordonnées \((0,y',z')\). Comme \(\overrightarrow{v}+\overrightarrow{v}'\) admet \((x+x',y+y',z+z')\) comme coordonnées, \(p(\overrightarrow{v}+\overrightarrow{v}')\) admet comme coordonnées \((0,y+y',z+z')\) qui sont aussi celles du vecteur \(p(\overrightarrow{v})+p(\overrightarrow{v}')\). Par conséquent, \(p(\overrightarrow{v})+p(\overrightarrow{v}')=p(\overrightarrow{v}+\overrightarrow{v}')\).
On a prouvé que \(p\) est linéaire.
Soit \(\lambda\) un réel. Le vecteur \(\lambda \, \overrightarrow{v}\) a pour coordonnées \((\lambda x, \lambda y, \lambda z)\). Les coordonnées de \(p(\lambda \overrightarrow{v})\) sont donc \((0,\lambda y,\lambda z)\) qui sont exactement les coordonnées de \(\lambda p(\overrightarrow{v})\). Donc \(p(\lambda \overrightarrow{v})=\lambda p(\overrightarrow{v})\).
La rotation \(r\) d’angle \({\scriptstyle\pi\over\scriptstyle 2}\) dans le plan orienté \((O,\overrightarrow{j},\overrightarrow{k})\) est linéaire.
Les vecteurs de ce plan sont ceux de coordonnées \((0,y,z)\). Soit \(\overrightarrow{v}\) un vecteur de ce plan. L’image par \(r\) de \(\overrightarrow{v}\) est le vecteur de coordonnées \((0,-z,y)\). On prouve la linéarité de cette application en passant aux coordonnées, comme dans la proposition précédente.
Soit \(k\) un réel non nul. L’homothétie \(h_k\) de rapport \(k\), qui à un vecteur \(\overrightarrow{v}\) de \(\mathscr V\) associe le vecteur \(k \overrightarrow{v}\) est linéaire.
Soient \(\overrightarrow{v}\) et \(\overrightarrow{v'}\) deux vecteurs de \(\mathscr V\). On a \[h_k(\overrightarrow{v}+
\overrightarrow{v'})=k(\overrightarrow{v}+ \overrightarrow{v'})=k \overrightarrow{v} + k \overrightarrow{v'}= h_k(\overrightarrow{v})+ h_k(\overrightarrow{v'}).\] Si \(\lambda\) est un réel, on a aussi \[h_k(\lambda \overrightarrow{v})=k (\lambda \overrightarrow{v})=\lambda h_k(\overrightarrow{v})\] ce qui prouve la linéarité de \(h\).
En particulier l’homothétie \(h\) de rapport \(k=\left\|\overrightarrow{u}\right\|\) est linéaire.
Cette proposition est une reformulation du théorème de Thalès.
Ces trois exemples vont nous permettre de démontrer que le produit vectoriel est bilinéaire.
(Le produit vectoriel est bilinéaire).
L’application \[\varphi: \left\{ \begin{array}{ccl} \mathscr V\times \mathscr V & \longrightarrow & \mathscr V \newline (\overrightarrow{u},\overrightarrow{v}) & \longmapsto & \overrightarrow{u} \wedge \overrightarrow{v} \end{array} \right.\] est bilinéaire. Autrement dit, pour tout vecteurs \(\overrightarrow{u}\), \(\overrightarrow{u_1}\), \(\overrightarrow{u_2}\), \(\overrightarrow{v}\), \(\overrightarrow{v_1}\), \(\overrightarrow{v_2}\) de \(\mathscr V\) et pour tout réels \(\lambda_1\), \(\lambda_2\) \[\boxed{\overrightarrow{u} \wedge(\lambda_1 \overrightarrow{v_1}+\lambda_2 \overrightarrow{v_2})=\lambda_1\overrightarrow{u} \wedge\overrightarrow{v_1}+\lambda_2\overrightarrow{u} \wedge\overrightarrow{v_2}} \quad \textrm{ et} \quad
\boxed{(\lambda_1 \overrightarrow{u_1}+\lambda_2 \overrightarrow{u_2})\wedge\overrightarrow{v}=\lambda_1\overrightarrow{u_1}\wedge\overrightarrow{v}+\lambda_2\overrightarrow{u_2} \wedge\overrightarrow{v}}.\]
Fixons \(\overrightarrow{u}\) dans \(\mathscr V\). L’application : \[\theta_{\overrightarrow{u}}: \left\{ \begin{array}{ccl} \mathscr V & \longrightarrow & \mathscr V \newline \overrightarrow{x} & \longmapsto & \overrightarrow{u} \wedge \overrightarrow{x} \end{array} \right.\] est linéaire comme composée des trois applications linéaires \(p\), \(r\) et \(h\). Pour montrer que \(\varphi\) est bilinéaire, il faut encore montrer que, pour \(\overrightarrow{v}\) fixé dans \(\mathscr V\) et pour tout \(\overrightarrow{u}\), \(\overrightarrow{u'}\) dans \(\mathscr V\) et \(\lambda\) réel, \[(\overrightarrow{u}+\overrightarrow{u'})\wedge \overrightarrow{v}=\overrightarrow{u} \wedge \overrightarrow{v}+\overrightarrow{u'}\wedge \overrightarrow{v}
\textrm{ et } (\lambda \overrightarrow{u})\wedge \overrightarrow{v} = \lambda \overrightarrow{u} \wedge \overrightarrow{v}\] Ces deux propriété découlent de l’antisymétrie du produit vectoriel et de la linéarité de \(\theta _{-\overrightarrow{v}}\). Par exemple pour la première égalité, on procède ainsi \[(\overrightarrow{u}+\overrightarrow{u'})\wedge \overrightarrow{v}= -\overrightarrow{v} \wedge (\overrightarrow{u}+\overrightarrow{u'}) = (-\overrightarrow{v}) \wedge (\overrightarrow{u}+\overrightarrow{u'})= \theta _{-\overrightarrow{v}}(\overrightarrow{u}+\overrightarrow{u'})=\theta _{-\overrightarrow{v}}(\overrightarrow{u})+
\theta _{-\overrightarrow{v}}(\overrightarrow{u'})=
-\overrightarrow{v} \wedge \overrightarrow{u} - \overrightarrow{v} \wedge \overrightarrow{u'}=\overrightarrow{u} \wedge \overrightarrow{v}+\overrightarrow{u'}\wedge
\overrightarrow{v}\]
Expression dans une base orthonormale directe
(Expression du produit vectoriel dans une base orthonormale). Soit \(\mathscr B\left(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)\) une base orthonormale directe. Soient \(\overrightarrow{u}\) et \(\overrightarrow{v}\) des vecteurs de \(\mathscr V\) de coordonnées respectives \(\left(x,y,z\right)\) et \(\left(x',y',z'\right)\) dans \(\mathscr B\). Les coordonnées \(\left(X,Y,Z\right)\) de \(\overrightarrow{u} \wedge \overrightarrow{v}\) sont données par :
Autrement dit : \[\boxed{\overrightarrow{u}\wedge \overrightarrow{v} \left|\begin{matrix} yz'-y'z \newline zx'-z'x \end{matrix} \right.{xy'-x'y}}\]
\[\boxed{ X=\left| \begin{array}{cc} y&y'\\ z &z' \end{array} \right|} \quad \boxed{ Y=\left| \begin{array}{cc} z&z'\\ x &x' \end{array} \right|} \quad \boxed{ X=\left| \begin{array}{cc} x&x'\\ y &y' \end{array} \right|}\]
(1). On a : \[\overrightarrow{u} = x\overrightarrow{i} + y \overrightarrow{j} + z\overrightarrow{k} \quad \textrm{ et} \quad\overrightarrow{v} = x'\overrightarrow{i} + y' \overrightarrow{j} + z'\overrightarrow{k}.\] Utilisant la bilinéarité du produit vectoriel et les relations \[\overrightarrow{i} \wedge \overrightarrow{j}= \overrightarrow{k} \quad \overrightarrow{j} \wedge \overrightarrow{i} = -\overrightarrow{k} \quad \overrightarrow{j}
\wedge \overrightarrow{k} = \overrightarrow{i} \quad \overrightarrow{k} \wedge \overrightarrow{j} = -\overrightarrow{i} \quad \overrightarrow{k} \wedge \overrightarrow{i}
= \overrightarrow{j} \quad \overrightarrow{i} \wedge \overrightarrow{k}= -\overrightarrow{j}\] \[\overrightarrow{i}\wedge \overrightarrow{i}= \overrightarrow{j}\wedge \overrightarrow{j}=\overrightarrow{k} \wedge \overrightarrow{k}=\overrightarrow{0}\] qui découlent du fait que \(\mathscr B\) est une base orthonormale directe, on peut écrire :
\[\begin{aligned} \overrightarrow{u} \wedge \overrightarrow{v} &=& \left(x\overrightarrow{i} + y \overrightarrow{j} + z\overrightarrow{k}\right) \wedge \left(x'\overrightarrow{i} + y' \overrightarrow{j} + z'\overrightarrow{k}.\right)\\ &=& xx'' \overrightarrow{i}\wedge \overrightarrow{i} + xy' \overrightarrow{i} \wedge \overrightarrow{j} + xz' \overrightarrow{i} \wedge \overrightarrow{k}\\ & & + yx' \overrightarrow{j} \wedge \overrightarrow{i} + yy' \overrightarrow{j} \wedge \overrightarrow{j} + yz' \overrightarrow{j} \wedge \overrightarrow{k} \\ & & + zx' \overrightarrow{k} \wedge \overrightarrow{i} + zy' \overrightarrow{k} \wedge \overrightarrow{j} + zz' \overrightarrow{k} \wedge \overrightarrow{k} \\ &=& xy' \overrightarrow{k} - xz' \overrightarrow{j} \\ & & - yx' \overrightarrow{k} + yz' \overrightarrow{i} \\ & & + zx' \overrightarrow{j} - zy' \overrightarrow{i} \newline &=& \left(yz'-y'z\right) \overrightarrow{i} + \left(zx'-z'x\right)\overrightarrow{j} + \left(xy'-x'y\right)\overrightarrow{k}\end{aligned}\] ce qu’il fallait démontrer.
Déterminant ou produit mixte
Définition
(Déterminant, produit mixte). Soient \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) trois vecteurs de l’espace \(\mathscr V\). On appelle déterminant ou produit mixte de ces trois vecteurs le nombre réel, noté \(\left[\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right]\) ou \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\), et donné par : \[\boxed{\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)=\left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w}}\]
Expression dans une base orthonormale directe
(Expression du déterminant dans une base orthonormale directe). Soit \(\mathscr B\left(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)\) une base orthonormale directe de \(\mathscr V\). Soient \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) trois vecteurs de \(\mathscr V\) et soient \(\left(x,y,z\right)\), \(\left(x',y',z'\right)\) et \(\left(x'',y'',z''\right)\) leurs coordonnées respectives dans cette base. Alors : \[\boxed{\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)=
\left|
\begin{array}{ccc}
x&x'&x''\\
y&y'&y''\\
z&z'&z''
\end{array}
\right|=
x'' \left|
\begin{array}{cc}
y&y'\\
z &z'
\end{array}
\right| -
y''\left|
\begin{array}{cc}
z&z'\\
x &x'
\end{array}
\right| +
z''\left|
\begin{array}{cc}
x&x'\newline
y &y'
\end{array}
\right|}\]
(1). Il suffit de calculer le produit mixte de ces trois vecteurs en utilisant les formules vues pour calculer le produit scalaire et le produit vectoriel de deux vecteurs dans une base orthonormale directe.
Propriétés du produit mixte
(Le produit mixte est antisymétrique). Soient \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) trois vecteurs de \(\mathscr V\).
On change le signe du produit mixte de trois vecteurs en permutant deux de ces trois vecteurs : \[\mathop{\rm det}\left(\overrightarrow{v},\overrightarrow{u},\overrightarrow{w}\right)=-\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right) \quad \left(1\right)\] \[\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{w},\overrightarrow{v}\right)=-\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right) \quad \left(2\right)\] \[\mathop{\rm det}\left(\overrightarrow{w},\overrightarrow{v},\overrightarrow{u}\right)=-\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right) \quad \left(3\right)\]
Le produit mixte est invariant par permutation circulaire \[\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)=\mathop{\rm det}\left(\overrightarrow{v},\overrightarrow{w},\overrightarrow{u}\right)=\mathop{\rm det}\left(\overrightarrow{w},\overrightarrow{u},\overrightarrow{v}\right) \quad \left(4\right)\]
(1).
Démontrons \(\left(1\right)\) : \[\begin{aligned} \mathop{\rm det}\left(\overrightarrow{v},\overrightarrow{u},\overrightarrow{w}\right)&=& \left(\overrightarrow{v}\wedge \overrightarrow{u}\right).\overrightarrow{w}\\ &=& \left(- \overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w} \textrm{ par antisymétrie du produit vectoriel}\\ &=& - \left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w}\newline &=& - \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\end{aligned}\]
Pour démontrer \(\left(4\right)\), il faut se placer dans une base orthonormale directe de \(\mathscr V\) et calculer, dans cette base, en utilisant la formule [Expression_base_ortho_prod_mixte], les trois déterminants \(\mathop{\rm det}\left(\overrightarrow{v},\overrightarrow{w},\overrightarrow{u}\right)\), \(\mathop{\rm det}\left(\overrightarrow{w},\overrightarrow{u},\overrightarrow{v}\right)\), \(det\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) et vérifier qu’ils sont égaux.
Pour démontrer \(\left(2\right)\), on peut remarquer que d’après \(\left(4\right)\), \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{w},\overrightarrow{v}\right) =\mathop{\rm det}\left(\overrightarrow{v},\overrightarrow{u},\overrightarrow{w}\right)\) et appliquer \(\left(1\right)\).
Enfin d’après \(\left(4\right)\) et \(\left(1\right)\), \(\mathop{\rm det}\left(\overrightarrow{w},\overrightarrow{v},\overrightarrow{u}\right)=\mathop{\rm det}\left(\overrightarrow{v},\overrightarrow{u},\overrightarrow{w}\right)=-\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\)
(Le produit mixte est alterné). Soient \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) trois vecteurs de \(\mathscr V\). Si deux de ces trois vecteurs sont égaux alors le produit mixte de ces trois vecteurs \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) est nul.
(1). Partant de l’égalité \(\mathop{\rm det}\left(\overrightarrow{v},\overrightarrow{u},\overrightarrow{w}\right)=-\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right),\) si \(\overrightarrow{u} = \overrightarrow{v}\), on obtient \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u},\overrightarrow{w}\right)=-\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u},\overrightarrow{w}\right)\) ce qui amène \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u},\overrightarrow{w}\right)=0\).
(Application trilinéaire). Une application \(\varphi:\mathscr V^3 \rightarrow 13 sqrt\) est dite trilinéaire si et seulement si :
pour tout \(\left(\overrightarrow{u},\overrightarrow{v}\right)\) fixé dans \(\mathscr V \times \mathscr V\), l’application : \(\overrightarrow{w} \mapsto \varphi\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) est linéaire.
pour tout \(\left(\overrightarrow{v},\overrightarrow{w}\right)\) fixé dans \(\mathscr V \times \mathscr V\), l’application : \(\overrightarrow{u} \mapsto \varphi\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) est linéaire.
pour tout \(\left(\overrightarrow{u},\overrightarrow{w}\right)\) fixé dans \(\mathscr V \times \mathscr V\), l’application : \(\overrightarrow{v} \mapsto \varphi\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) est linéaire.
Le produit mixte est trilinéaire.
Fixons \(\left(\overrightarrow{u},\overrightarrow{v}\right)\) dans \(\mathscr V \times \mathscr V\) et montrons que l’application : \(\varphi~: \overrightarrow{w} \mapsto \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) est linéaire. Soient \(\alpha\), \(\alpha'\) deux scalaires et \(\overrightarrow{w}\), \(\overrightarrow{w}'\) deux vecteurs de \(\mathscr V\). On a \[\begin{aligned} \varphi\left(\alpha \overrightarrow{w} + \alpha' \overrightarrow{w}'\right)&=&\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\alpha \overrightarrow{w} + \alpha' \overrightarrow{w}'\right)\\ &=& \left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\left(\alpha \overrightarrow{w} + \alpha' \overrightarrow{w}'\right)\\ &=& \alpha \left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w} + \alpha' \left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w}' \textrm{ par linéarité du produit scalaire}\\ &=&\alpha \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right) + \alpha' \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}'\right)\newline &=&\alpha \varphi\left(\overrightarrow{w}\right) + \alpha' \varphi\left(\overrightarrow{w}'\right)\end{aligned}\]
Fixons maintenant \(\left(\overrightarrow{u},\overrightarrow{w}\right)\) dans \(\mathscr V \times \mathscr V\) et montrons que l’application \(\varphi~: \overrightarrow{v} \mapsto \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) est linéaire. Il suffit de remarquer que pour tout \(\overrightarrow{v}\) dans \(\mathscr V\), comme le produit mixte est antisymétrique, \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)=-\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{w},\overrightarrow{v}\right)\) et que l’application \(\overrightarrow{v} \mapsto -\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{w},\overrightarrow{v}\right)\) est, d’après le premier point, linéaire.
On montre la linéarité de \(\overrightarrow{u} \mapsto \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) de la même façon.
Interprétation géométrique
(Trois vecteurs sont coplanaires si et seulement si leur produit mixte est nul). Soient \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) trois vecteurs de \(\mathscr V\). Ces trois vecteurs sont coplanaires si et seulement si leur produit mixte est nul.
(1). Si un des trois vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) est nul, le résultat est clair. On suppose donc désormais qu’aucun de ces trois vecteurs n’est nul.
Supposons que \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) sont coplanaires. Une des deux assertions suivantes est alors vraie :
\(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires et on a donc \(\overrightarrow{u} \wedge \overrightarrow{v} = \overrightarrow{0}\) ce qui entraine que \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right) = \left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w} = 0\).
\(\overrightarrow{u}\) et \(\overrightarrow{v}\) ne sont pas colinéaires et donc \(\overrightarrow{u} \wedge \overrightarrow{v}\) est un vecteur orthogonal au plan engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\). Comme \(\overrightarrow{w}\) est élément de ce plan, \(\overrightarrow{u} \wedge \overrightarrow{v}\) est orthogonal à \(\overrightarrow{w}\) et nécessairement : \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right) = \left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w} = 0\)
Supposons que \(\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right) =0\). Alors :
si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont colinéaires, il est clair que \(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\) sont coplanaires...(ces trois vecteurs sont éléments du plan engendré par \(\overrightarrow{u}\) et \(\overrightarrow{w}\)).
sinon, \(\overrightarrow{u} \wedge \overrightarrow{v}\) est un vecteur orthogonal au plan engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\) et comme \(\left(\overrightarrow{u} \wedge \overrightarrow{v}\right).\overrightarrow{w} = 0\), \(\overrightarrow{w}\) est aussi orthogonal à \(\overrightarrow{u} \wedge \overrightarrow{v}\) et est donc nécessairement élément de ce plan.
(Interprétation du produit mixte en terme de volume). Soient \(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{w}\) trois vecteurs de \(\mathscr V\). Notons \(\mathcal V\) le volume du parallélépipède \(\mathcal P\) construit à partir de ces \(3\) vecteurs. On a : \[\boxed{\mathcal V = \left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\right|}\]
(1). Si les trois vecteurs sont coplanaires, le résultat est évident. On suppose donc que ce n’est pas le cas. Soient \(O\), \(A\), \(B\) et \(C\) des points de l’espace tels que \(\overrightarrow{u} = \overrightarrow{OA}\), \(\overrightarrow{v} = \overrightarrow{OB}\) et \(\overrightarrow{w} = \overrightarrow{OC}\).
Soit \(H\) le projeté orthogonal de \(C\) sur la droite dirigée par \(\overrightarrow{u} \wedge \overrightarrow{v}\). \(OH\) est la hauteur du parallélépipède \(\mathcal P\). \(OH\) est donnée par :\[OC \left|\cos\left(\overrightarrow{u} \wedge \overrightarrow{v},\overrightarrow{w}\right)\right| = \left\|\overrightarrow{w}\right\| \left|\cos\left(\overrightarrow{u} \wedge \overrightarrow{v},\overrightarrow{w}\right)\right|\]
Le parallélogramme formant la base de \(\mathcal P\) est porté par les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) et son aire \(\mathcal A\) est donnée par : \[\left|\left\|\overrightarrow{u}\right\| \left\|\overrightarrow{v}\right\| \sin\left(\overrightarrow{u}, \overrightarrow{v}\right)\right|=\left\|\overrightarrow{u} \wedge \overrightarrow{v}\right\|\]
Plans dans l’espace
Représentation paramétrique des plans
(Équation paramétrique d’un plan).
Le système \[\boxed{\begin{cases}
x=x_A+\alpha x_{\overrightarrow{u}} + \beta x_{\overrightarrow{v}}\\
y=y_A+\alpha y_{\overrightarrow{u}} + \beta y_{\overrightarrow{v}}\newline
z=z_A+\alpha z_{\overrightarrow{u}} + \beta z_{\overrightarrow{v}}
\end{cases}}\] est une équation paramétrique de \(\mathscr P\).
Soit \(\mathscr R\left(O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)\) un repère de l’espace \(\mathscr E\). Soient : \(A\left(x_A,y_A,z_A\right)\in\mathscr E\), \(\overrightarrow{u}\left(x_{\overrightarrow{u}},y_{\overrightarrow{u}},z_{\overrightarrow{u}}\right)\) et \(\overrightarrow{v}\left(x_{\overrightarrow{v}},y_{\overrightarrow{v}},z_{\overrightarrow{v}}\right)\) deux vecteurs de \(\mathscr V\). Soient \(M\left(x,y,z\right)\) un point de l’espace et \(\mathscr P\) le plan affine passant par \(A\) et engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\). On a équivalence entre :
\(M\) est élément de \(\mathscr P\)
il existe \(\left(\alpha,\beta\right)\in13 sqrt ^2\) tel que \(\overrightarrow{AM}=\alpha \overrightarrow{u} + \beta \overrightarrow{v}\).
il existe \(\left(\alpha,\beta\right)\in13 sqrt ^2\) tel que : \[\begin{cases} x=x_A+\alpha x_{\overrightarrow{u}} + \beta x_{\overrightarrow{v}}\\ y=y_A+\alpha y_{\overrightarrow{u}} + \beta y_{\overrightarrow{v}}\\ z=z_A+\alpha z_{\overrightarrow{u}} + \beta z_{\overrightarrow{v}} \end{cases}\]
Soit \(M\left(x,y,z\right)\) un point de l’espace. Supposons que \(M\) est élément du plan \(\mathscr P\) alors le vecteur \(\overrightarrow{AM}\) est combinaison linéaire des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\). Autrement dit, il existe des scalaires \(\alpha,\beta\in13 sqrt\) tels que \(\overrightarrow{AM}=\alpha \overrightarrow{u} + \beta \overrightarrow{v}\). En récrivant cette égalité avec des coordonnées, on obtient \(\begin{cases}
x=x_A+\alpha x_{\overrightarrow{u}} + \beta x_{\overrightarrow{v}}\\
y=y_A+\alpha y_{\overrightarrow{u}} + \beta y_{\overrightarrow{v}}\newline
z=z_A+\alpha z_{\overrightarrow{u}} + \beta z_{\overrightarrow{v}}
\end{cases}\).
Réciproquement, si les coordonnées du point \(M\left(x,y,z\right)\) vérifient le système précédentes, on montre que \(\overrightarrow{AM}=\alpha \overrightarrow{u} + \beta \overrightarrow{v}\) et donc que \(M\in\mathscr P\).
Représentation cartésienne
Pour tout ce paragraphe, on fixe un repère orthonormal direct \(\mathscr R\left(O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)\) de l’espace \(\mathscr E\).
Soit \(\mathscr P\) un plan affine de \(\mathscr E\) Soit \(A\) un point de \(\mathscr
P\) et \(\left(\overrightarrow{u},\overrightarrow{v}\right)\) un couple de vecteurs engendrant \(\mathscr P\). On a équivalence entre :
le point \(M\) est élément de \(\mathscr P\).
le produit mixte \(\mathop{\rm det}\left(\overrightarrow{AM},\overrightarrow{u},\overrightarrow{v}\right)\) est nul.
(1). Si \(M\in\mathscr P\) alors \(\overrightarrow{AM}\) est combinaison linéaire de \(\overrightarrow{u}\) et \(\overrightarrow{v}\) et les vecteurs \(\overrightarrow{AM}\), \(\overrightarrow{u}\), \(\overrightarrow{v}\) sont coplanaires. On a alors nécessairement \(\mathop{\rm det}\left(\overrightarrow{AM},\overrightarrow{u},\overrightarrow{v}\right)=0\).
Réciproquement, si \(\mathop{\rm det}\left(\overrightarrow{AM},\overrightarrow{u},\overrightarrow{v}\right)=0\) alors les vecteurs \(\overrightarrow{AM}\), \(\overrightarrow{u}\), \(\overrightarrow{v}\) sont coplanaires ce qui n’est possible que si le point \(M\) est dans le même plan que celui passant par \(A\) et engendré par \(\overrightarrow{u}\), \(\overrightarrow{v}\), c’est-à-dire \(\mathscr P\) (car \(\overrightarrow{u}\) et \(\overrightarrow{v}\) ne sont pas colinéaires par hypothèse).
Soient \(A\left(x_A,y_A,z_A\right)\), \(B\left(x_B,y_B,z_B\right)\), \(C\left(x_C,y_C,z_C\right)\) trois points non alignés de l’espace \(\mathscr E\). Alors \(M\left(x,y,z\right)\in\mathscr E\) est élément du plan affine \(\mathscr P\) passant par \(A\), \(B\) et \(C\) si et seulement si \[\left|
\begin{array}{ccc}
x-x_A&x_B-x_A&x_C-x_A\\
y-y_A&y_B-y_A&y_C-y_A\newline
z-z_A&z_B-z_A&z_C-z_A
\end{array}
\right|=0\]
Il suffit d’appliquer la proposition précédente à \(\overrightarrow{u} = \overrightarrow{AB}\) et \(\overrightarrow{v} = \overrightarrow{AC}\) et d’exprimer le produit mixte avec les coordonnées de ces vecteurs.
(Équation cartésienne d’un plan).
Soit \(\mathscr P\) un plan affine passant par un point \(A\left(x_A,y_A,z_A\right)\) de l’espace \(\mathscr E\) et admettant le vecteur \(\overrightarrow{n} \left(a,b,c\right)\) comme vecteur normal alors une équation cartésienne de \(\mathscr P\) est \[\boxed{a\left(x-x_A\right)+b\left(y-y_A\right)+c\left(z-z_A\right)=0}\]
Réciproquement, l’ensemble des points \(M\left(x,y,z\right)\) vérifiant l’équation \(ax+by+cz=d\) où \(a\), \(b\), \(c\), \(d\) sont des réels et où \(a\), \(b\), \(c\) ne sont pas tous nuls est un plan affine de vecteur normal \(\boxed{\overrightarrow{n}\left(a,b,c\right)}\).
\(M\) est élément de \(\mathscr P\) si et seulement si \(\overrightarrow{AM}\) et \(\overrightarrow{n}\) sont orthogonaux et donc si et seulement si \(\overrightarrow{AM}.\overrightarrow{n}=0\). Exprimant cette dernière égalité avec les coordonnées des vecteurs considérés, on retrouve la formule proposée.
Si \(a\neq 0\), posons \(A\left(-{\scriptstyle d\over\scriptstyle a},0,0\right)\) sinon, si \(b\neq 0\), posons \(A\left(0,-{\scriptstyle d\over\scriptstyle b},0\right)\) sinon on a forcément \(c\neq 0\) et nous posons \(A\left(0,0,-{\scriptstyle d\over\scriptstyle c}\right)\). Comme le point \(M\left(x,y,z\right)\) vérifie l"équation \(ax+by+cz=d\), on a \(\overrightarrow{AM}.\overrightarrow{n}=0\) et donc \(M\) est un point du plan passant par \(A\) et de vecteur normal \(\overrightarrow{n}\).
(Équation normale d’un plan). Soit \(\mathscr P\) un plan affine d’équation \(ax+by+cz=d\). Comme dit plus haut, le vecteur \(\overrightarrow{n}\left(a,b,c\right)\) est un vecteur normal à \(\mathscr P\). Si ce vecteur est de plus unitaire, c’est-à-dire si \[\left\|\overrightarrow{n}\right\|^2 = a^2+b^2+c^2 = 1\] alors l’équation \(ax+by+cz=d\) est appelée équation normale de \(\mathscr P\).
Interprétation géométrique de l’équation normale
Soit \(\mathscr P\) un plan et \(H\) le projeté orthogonal de l’origine \(O\) de \(\mathscr R\) sur \(\mathscr P\). Posons : \(\overrightarrow{u} = {\scriptstyle\overrightarrow{OH}\over\scriptstyle\left\|\overrightarrow{OH}\right\|}\). Considérons les \(3\) angles non orientés :
\[\alpha=\left(\overrightarrow{i},\overrightarrow{u}\right), \quad \beta=\left(\overrightarrow{j},\overrightarrow{u}\right) \quad \textrm{ et} \quad\gamma=\left(\overrightarrow{k},\overrightarrow{u}\right)\]
On a donc
\[\cos \alpha = \overrightarrow{i} . \overrightarrow{u}, \quad \cos \beta = \overrightarrow{j} . \overrightarrow{u} \quad \textrm{ et} \quad\cos \gamma = \overrightarrow{k} . \overrightarrow{u}\] et \(\overrightarrow{u} \left(\cos \alpha,\cos \beta,\cos \gamma\right)\). Comme \(\overrightarrow{u}\) est unitaire, on a aussi \(\cos^2 \alpha+\cos^2\beta + \cos^2 \gamma=1\). Par ailleurs
\[\begin{aligned} M\left(x,y,z\right)\in\mathscr P&\Longleftrightarrow& \overrightarrow{HM}.\overrightarrow{u} = 0\\ &\Longleftrightarrow& \left(\overrightarrow{OM} - \overrightarrow{OH}\right).\overrightarrow{u} =0\\ &\Longleftrightarrow& \left(x \overrightarrow{i} + y \overrightarrow{j} + z\overrightarrow{k} - h \overrightarrow{u}\right). \overrightarrow{u}=0 \textrm{ où $h=\left\|\overrightarrow{OH}\right\|$}\newline &\Longleftrightarrow& \cos \alpha x + \cos \beta y + \cos \gamma z=h .\end{aligned}\]
Cette dernière égalité forme une équation normale de \(\mathscr P\).
Position relative de deux plans
L’espace est ici encore rapporté à un repère orthonormal direct \(\mathscr R\left(O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)\).
(Plans parallèles). Deux plans de l’espace sont parallèles si et seulement si ils admettent un vecteur normal non nul commun.
(Plans perpendiculaires). Deux plans de l’espace sont perpendiculaires si et seulement si ils admettent des vecteurs normaux non nuls orthogonaux.
(Caractérisation de la perpendicularité ou du parallélisme de deux plans à partir de leurs équations cartésiennes respectives).
Soient \(\mathscr P\) et \(\mathscr P'\) deux plans d’équations cartésiennes respectives \[ax+by+cz=d \quad \textrm{ et} \quad a'x+b'y+c'z=d'.\] Les vecteurs \(\overrightarrow{n}\left(a,b,c\right)\) et \(\overrightarrow{n}'\left(a',b',c'\right)\) sont donc, respectivement, des vecteurs normaux à \(\mathscr P\) et à \(\mathscr P'\).
Les plans \(\mathscr P\) et \(\mathscr P'\) sont parallèles si et seulement si il existe un réel \(\lambda\neq 0\) tel que \[a'=\lambda a, \quad b'=\lambda b \quad \textrm{ et} \quad c'=\lambda c\]
Les plans \(\mathscr P\) et \(\mathscr P'\) sont confondues si et seulement si il existe un réel \(\lambda\neq 0\) tel que \[a'=\lambda a, \quad b'=\lambda b ,\quad c'=\lambda c \quad \textrm{ et} \quad d'=\lambda d\]
Les plans \(\mathscr P\) et \(\mathscr P'\) sont perpendiculaires si et seulement si \[aa'+bb'+cc'=0\]
(1).
\(\mathscr P\) et \(\mathscr P'\) sont parallèles si et seulement si leurs vecteurs normaux sont colinéaires ce qui est se traduit en termes de coordonnées par les \(3\) égalités ci dessus.
\(\mathscr P\) et \(\mathscr P'\) sont confondues si et seulement si, à la fois, ils sont parallèles et si ils ont un point commun \(A\left(x_A,y_A,z_A\right)\). D’après le point précédent, ceci est équivalent à \[a'=\lambda a, \quad b'=\lambda b ,\quad c'=\lambda c \quad \textrm{ et} \quad a x_A + b y_A + c z_A -d= a' x_A + b' y_A + c' z_A -d' =0\] On obtient alors \[\left(\lambda a -a\right) x_A + \left(\lambda b -b\right) y_A+ \left(\lambda c -c\right) z_A -d+d'=0\] ou encore \[\left(\lambda - 1\right)\left( a x_A + b y_A+ c z_A\right) -d+d'=0\] Et comme \(A\) est élément de \(\mathscr P\), on a aussi \[\left(\lambda - 1\right) d -d+d'=0\] Ce qui prouve que \(d'=\lambda d\)
Les deux plans sont perpendiculaires si et seulement si leurs vecteurs normaux sont orthogonaux, c’est-à-dire si et seulement si \(\overrightarrow{n} . \overrightarrow{n}'=0\), de quoi découle l’égalité à prouver quand on la transcrit en coordonnées.
Soient \(\mathscr P\) et \(\mathscr P'\) deux plans de l’espace de vecteurs normaux respectifs \(\overrightarrow{n}\) et \(\overrightarrow{n}'\). Si \(\mathscr P\) et \(\mathscr P'\) sont sécants alors leur intersection est une droite de vecteur directeur \(\overrightarrow{n}
\wedge \overrightarrow{n}'\).
(1). Soit \(A\) un point de l’intersection des deux plans \(\mathscr P\) et \(\mathscr
P'\).
Réciproquement, supposons que \(M\) appartient à la droite passant par \(A\) dirigée par \(\overrightarrow{n} \wedge \overrightarrow{n}'\), alors le vecteur \(\overrightarrow{AM}\) est orthogonal à \(\overrightarrow{n}\) et à \(\overrightarrow{n}'\). Comme \(A\) est élément des plans \(\mathscr
P\) et \(\mathscr P'\), nécessairement \(M\) est élément de \(\mathscr
P\) et \(\mathscr P'\) et donc de \(\mathscr
P \cap \mathscr P'\).
Si le point \(M\) est élément de \(\mathscr P \cap \mathscr P'\) alors \(\overrightarrow{AM}\) est orthogonal à \(\overrightarrow{n}\) et à \(\overrightarrow{n}'\). Par conséquent, \(\overrightarrow{AM}\) est colinéaire à \(\overrightarrow{n} \wedge \overrightarrow{n}'\) et \(M\) appartient à la droite passant par \(A\) dirigée par \(\overrightarrow{n} \wedge \overrightarrow{n}'\).
Distance d’un point à un plan
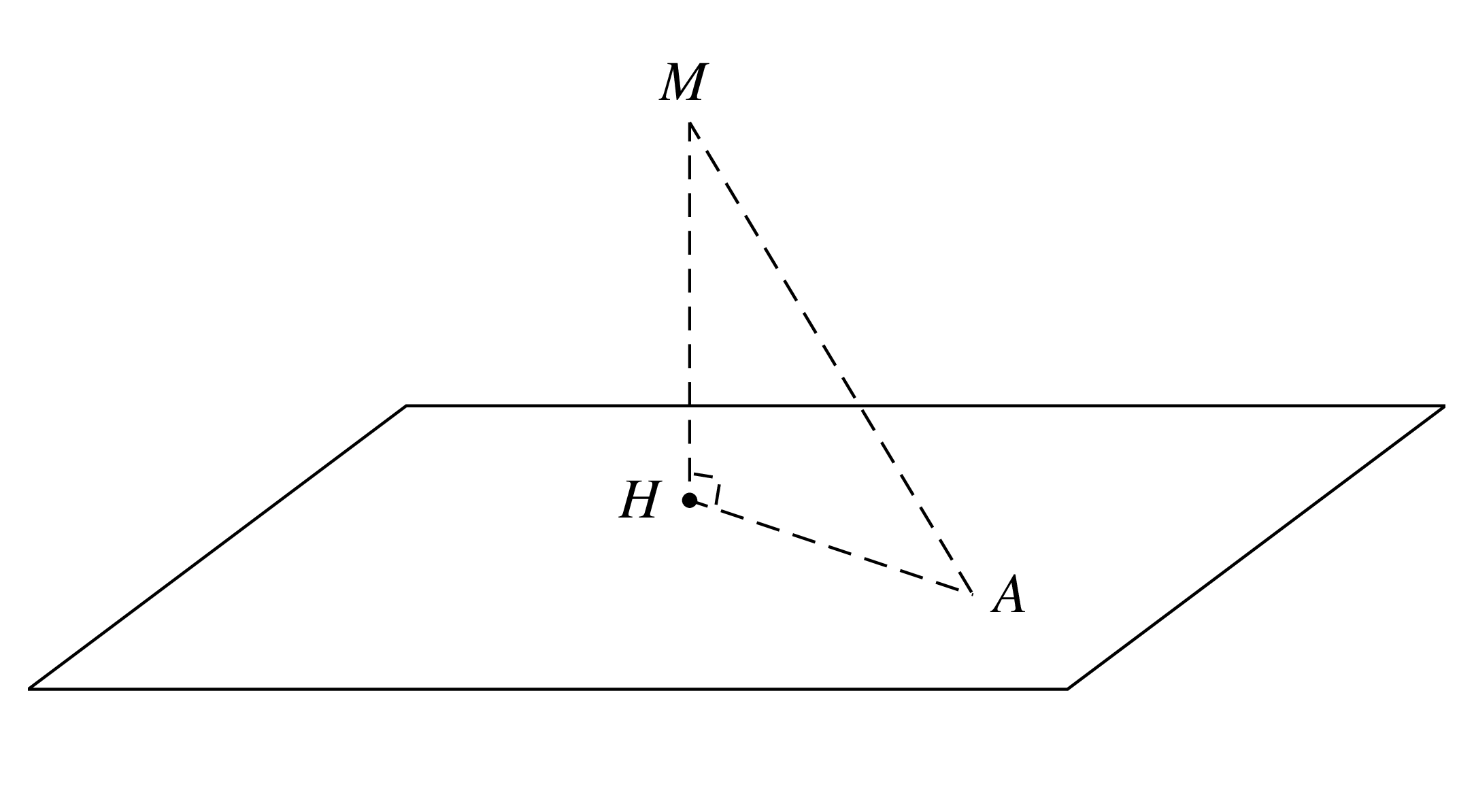
(Distance d’un point à un plan). Soit \(\mathscr P\) un plan affine de vecteur normal \(\overrightarrow{n}\). Soit \(M\) un point de l’espace et \(H\) son projeté orthogonal sur \(\mathscr P\). On appelle distance du point \(M\) au plan \(\mathscr P\) la distance \(MH\). On la note : \(d\left(M,\mathscr P\right)\). C’est la plus petite distance du point \(M\) à un point \(A\) de \(\mathscr P\) : \[\forall A\in\mathscr P,\quad d\left(M,\mathscr P\right) = HM \leqslant AM.\]
(1). Soit \(A\in \mathscr P\). Le théorème de Pythagore appliqué dans le triangle \(AHM\) permet d’écrire \(AH^2+HA^2=AM^2\). Comme \(HA^2\geqslant 0\), on a \(MH^2\leqslant AM^2\) et donc \(MH\leqslant
MA\).
\(H\) est l’unique point de \(\mathscr P\) tel que les vecteurs \(\overrightarrow{MH}\) et \(\overrightarrow{n}\) sont colinéaires.
Deux méthodes de calcul de la distance d’un point à un plan
(Distance d’un point à un plan quand le plan est donné par un point et deux vecteurs directeurs). Soit \(\mathscr P\) un plan défini passant par un point \(A\), engendré par les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) et de vecteur normal \(\overrightarrow{n}\). Soit \(M\) un point de l’espace. On a \[\boxed{d\left(M,\mathscr P\right) =\dfrac{\left|{\overrightarrow{n}}\cdot
\overrightarrow{AM}\right|}{\left\|\overrightarrow{n}\right\|}= \dfrac{\left|\left(\overrightarrow{u} \wedge \overrightarrow{v}\right)\cdot
\overrightarrow{AM}\right|}{\left\|\overrightarrow{u} \wedge \overrightarrow{v}\right\|} = \dfrac{\left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{AM}\right)\right|}{\left\|\overrightarrow{u} \wedge \overrightarrow{v}\right\|}}\]
(2). Soit \(H\) le projeté orthogonal de \(M\) sur \(\mathscr P\). Plaçons nous dans le plan défini par les points \(A\), \(H\) et \(M\). Soit \(\theta\) une mesure de l’angle non orienté \(\left(\overrightarrow{n},\overrightarrow{MA}\right)\). On a \(MH=AM\cdot \left|\cos \theta\right|.\)
Par ailleurs \[\begin{aligned} MH =AM\cdot \left|\cos \theta\right|=\dfrac{\left\|\overrightarrow{n}\right\|\left\|\overrightarrow{AM}\right\|\left|\cos \theta\right|}{\left\|\overrightarrow{n}\right\|}=\dfrac{\left|{\overrightarrow{n}}\cdot \overrightarrow{AM}\right|}{\left\|\overrightarrow{n}\right\|}\end{aligned}\]
ce qui prouve la première formule. Pour la seconde, il suffit d’appliquer la première avec \(\overrightarrow{n}=\overrightarrow{u} \wedge \overrightarrow{v}\) qui est bien un vecteur normal à \(\mathscr P\). Enfin, par définition, on sait que \(\left(\overrightarrow{u} \wedge \overrightarrow{v}\right) \cdot \overrightarrow{AM}=\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{AM}\right)\)
(Distance d’un point à un plan quand le plan est donné par une équation cartésienne). On rapporte le plan à un repère orthonormal \(\mathscr R\). Soient \(\mathscr P\) un plan d’équation cartésienne \(ax+by+cz+d=0\) et \(M\left(x_M,y_M,z_M\right)\) un point de l’espace. On a \[\boxed{d\left(M,\mathscr P\right) =
\dfrac{\left|ax_M+by_M+cz_M+d\right|}{\sqrt{a^2+b^2+c^2}}}\]
(1). Au regard de l’équation cartésienne de \(\mathscr P\) le vecteur \(\overrightarrow{n}
\left(a,b,c\right)\) est normal pour \(\mathscr P\). On considère un point \(A\left(x_A,y_A,z_A\right)\in\mathscr P\). En utilisant la formule précédente, on obtient \[\begin{aligned}
d\left(M,\mathscr P\right) &=& \dfrac{\left|\overrightarrow{n}\cdot
\overrightarrow{AM}\right|}{\left\|\overrightarrow{n}\right\|} \\
&=&\dfrac{\left|a\left(x_M-x_A\right)+b\left(y_M-y_A\right)+c\left(z_M-z_A\right)\right|
}{\sqrt{a^2+b^2+c^2}}\\
&=&\dfrac{\left|ax_M+by_M+cz_M-\left(ax_A+by_A+cz_A\right)\right|
}{\sqrt{a^2+b^2+c^2}}\newline
&=&\dfrac{
\left|ax_M+by_M+cz_M+d\right|}{\sqrt{a^2+b^2+c^2}}\end{aligned}\] car comme \(A\) est élément de \(\mathscr P\), on a \(ax_A+by_A+cz_A=-d\).
Droites dans l’espace
Représentation paramétrique
(Représentation paramétrique d’une droite). Soit \(\mathscr R\) un repère orthonormal de l’espace. Soit \(\mathscr D\) une droite passant par un point \(A\left(x_A,y_A,z_A\right)\) et de vecteur directeur \(\overrightarrow{u}\left(x_{\overrightarrow{u}},y_{\overrightarrow{u}},z_{\overrightarrow{u}}\right)\). Une équation paramétrique de \(\mathscr D\) est : \[\boxed{\begin{cases}
x=x_A+t x_{\overrightarrow{u}}\\
y=y_A+t y_{\overrightarrow{u}}\newline
z=z_A+t z_{\overrightarrow{u}}
\end{cases}}\]
Il s’agit d’une traduction en termes de coordonnées de l’égalité \(\exists
\lambda \in13 sqrt : \quad \overrightarrow{v} = \lambda \overrightarrow{u}\).
Représentation cartésienne
(Représentation cartésienne d’une droite).
Réciproquement, toute droite admet au moins un système d’équations de ce type.
Soit \(\mathscr R\) un repère orthonormal de l’espace. On se donne des réels \(a,b,c,d\) et \(a',b',c',d'\) tels que les triplets \(\left(a,b,c\right)\) et \(\left(a',b',c'\right)\) sont non nuls et non proportionnels. L’ensemble des points du plan dont les coordonnées vérifient le système \[\left(\star\right)\quad \boxed{\begin{cases} ax+by+cz+d=0\newline a'x+b'y+c'z+d'=0 \end{cases}}\] est une droite de vecteur directeur \(\boxed{\overrightarrow{n} \wedge \overrightarrow{n}'}\) où \(\overrightarrow{n} \left(a,b,c\right)\) et \(\overrightarrow{n}' \left(a',b',c'\right)\).
Les triplets \(\left(a,b,c\right)\) et \(\left(a',b',c'\right)\) n’étant pas proportionnels, les vecteurs normaux au plan \(\mathscr P\) d’équation \(ax+by+cz+d=0\) et \(\mathscr P'\) d’équation \(a'x+b'y+c'z+d'=0\) ne sont pas colinéaires et ces deux plans ne sont pas parallèles. Leur intersection forme donc une droite affine d’après la proposition [intersection_plans]. Un système d’équations cartésiennes pour cette droite est donné par le système \(\left(\star\right)\).
Réciproquement, si \(\mathscr D\) est une droite affine dirigée par \(\overrightarrow{u} \in
\mathscr V\) et passant par \(A\in\mathscr V\), alors si on complète le vecteur \(\overrightarrow{v}\) en un trièdre direct \(\left(\overrightarrow{u},\overrightarrow{v},\overrightarrow{w}\right)\) de l’espace, il est clair que \(\mathscr D\) est l’intersection des plans passant par \(\mathscr P\left(A,\overrightarrow{u},\overrightarrow{v}\right)\) et \(\mathscr P\left(A,\overrightarrow{u},\overrightarrow{w}\right)\). La droite \(\mathscr D\) admet donc bien un système d’équations du type indiqué.
Distance d’un point à une droite
(Distance d’un point à une droite). Soit \(\mathscr D\) une droite de l’espace passant par le point \(P\) et de vecteur directeur \(\overrightarrow{u}\). Soit \(A\) un point de l’espace et \(H\) son projeté orthogonal sur \(\mathscr D\) (\(H\) est l’unique point de \(\mathscr D\) tel que les vecteurs \(\overrightarrow{AH}\) et \(\overrightarrow{u}\) sont orthogonaux). On appelle distance de \(A\) à \(\mathscr D\) la distance \(AH\). C’est la plus petite distance de \(A\) à un point de \(\mathscr D\). Elle est notée \(d\left(A,\mathscr D\right)\).
Voir la preuve de la proposition [distancepointplan].
Soit \(\mathscr D\) une droite de l’espace passant par le point \(A\) et de vecteur directeur \(\overrightarrow{u}\). Soit \(M\) un point de l’espace. On a \[\boxed{d\left(M,\mathscr D\right) = {\scriptstyle\left\|\overrightarrow{u} \wedge
\overrightarrow{AM}\right\|\over\scriptstyle\left\|\overrightarrow{u}\right\|} }\]
(1). Soient \(H\) le projeté orthogonal de \(M\) sur la droite \(\mathscr D\). Soit \(\theta\) une mesure de l’angle non orienté \(\left(\overrightarrow{AH},\overrightarrow{AM}\right)\). On a : \(AH=AM \left|\sin \theta\right|\). Par ailleurs, on a \[\left\|\overrightarrow{u} \wedge \overrightarrow{AM}\right\| = \left\|\overrightarrow{u}\right\| \left\|\overrightarrow{AM}\right\| \left|\sin
\theta\right|\] d’où l’égalité.
Perpendiculaire commune à deux droites
(Droites orthogonales, droites perpendiculaires).
Deux droites affines de l’espace sont orthogonales si et seulement si leurs vecteurs directeurs le sont.
Deux droites affines de l’espace sont perpendiculaires si et seulement si elles sont à la fois sécantes et orthogonales.
Si \(\mathscr D\) et \(\mathscr D'\) sont deux droites parallèles, il existe une infinité de perpendiculaires commune à ces deux droites. Elle effet, elles sont contenues dans un même plan et il existe une infinité de droites perpendiculaires à ce plan.
(Perpendiculaire commune à deux droites). Soient \(\mathscr D\) et \(\mathscr D'\) deux droites non parallèles, il existe une unique droite \(\Delta\) perpendiculaire à la fois à \(\mathscr D\) et à \(\mathscr
D'\). Cette droite est appelée perpendiculaire commune aux deux droites \(\mathscr D\) et à \(\mathscr D'\). Si de plus \(\mathscr D\) est dirigée par \(\overrightarrow{u}\) et si \(\mathscr D'\) est dirigée par \(\overrightarrow{u}'\) alors \(\Delta\) est dirigée par \(\overrightarrow{u} \wedge \overrightarrow{u}'\).
(1).
Soient :
\(\overrightarrow{u}\) un vecteur directeur de \(\mathscr D\) et \(A\) un point de \(\mathscr D\)
\(\overrightarrow{u}'\) un vecteur directeur de \(\mathscr D'\) et \(A'\) un point de \(\mathscr D'\).
Posons \(\overrightarrow{w} = \overrightarrow{u} \wedge \overrightarrow{u}'\). Comme les droites \(\mathscr D\) et \(\mathscr D'\) ne sont pas parallèles, leurs vecteurs directeurs ne sont pas colinéaires et donc \(\overrightarrow{w}\) est non nul. Notons \(\mathscr P\) le plan donné par le triplet \(\left(A,\overrightarrow{u},\overrightarrow{w}\right)\) et \(\mathscr P'\) le plan donné par le triplet \(\left(A',\overrightarrow{u}',\overrightarrow{w}\right)\). Un vecteur normal à \(\mathscr P\) est \(\overrightarrow{n}=\overrightarrow{u}\wedge\overrightarrow{w}\) et un vecteur normal à \(\mathscr P'\) est \(\overrightarrow{n}'=\overrightarrow{u}'\wedge\overrightarrow{w}\). Ces deux plans ne sont pas parallèles. En effet, si c’était le cas, alors \(\overrightarrow{n}\) et \(\overrightarrow{n}'\) seraient colinéaires. Il existerait donc des scalaires \(\alpha,\beta\) non tous deux nuls tels que \(\alpha\overrightarrow{u}\wedge\overrightarrow{w} +\beta \overrightarrow{u}'\wedge\overrightarrow{w} =\overrightarrow{0}\) ce qui amènerait \(\left(\alpha\overrightarrow{u}+\beta \overrightarrow{u}'\right)\wedge\overrightarrow{w} =\overrightarrow{0}\). Alors \(\overrightarrow{w}\) serait élément du plan vectoriel engendré par \(\overrightarrow{u}\) et \(\overrightarrow{u}'\) ce qui n’est pas possible par définition de \(\overrightarrow{w}\). L’intersection des plans \(\mathscr P\) et \(\mathscr P'\) est donc une droite affine \(\Delta\) qui est dirigée par \(\overrightarrow{w}\) et donc perpendiculaire aux deux droites \(\mathscr D\) et \(\mathscr D'\).
Soit \(\Delta'\) une droite affine perpendiculaire aux deux droites \(\mathscr D\) et \(\mathscr D'\). Alors un vecteur directeur \(\overrightarrow{w}'\) de \(\Delta'\) est orthogonal à la fois à \(\overrightarrow{u}\) et à \(\overrightarrow{u}'\). Autrement dit \(\overrightarrow{w}'\) est colinéaire à \(\overrightarrow{w} = \overrightarrow{u} \wedge \overrightarrow{u}'\). De plus, \(\Delta'\) est incluse dans le plan affine \(\left(A,\overrightarrow{u},\overrightarrow{w}\right)\) ainsi que dans le plan \(\left(A',\overrightarrow{u}',\overrightarrow{w}\right)\). Par conséquent \(\Delta'=\delta\).
(Pour déterminer la perpendiculaire commune à deux droites). Dans l’espace muni d’un repère orthonormal direct, on considère deux droites non coplanaires \(\mathcal D\) et \(\mathcal D'\) telles que
\(\mathcal D\) est dirigée par le vecteur \(\overrightarrow{u}\) et passe par le point \(A\)
\(\mathcal D'\) est dirigée par le vecteur \(\overrightarrow{u}'\) et passe par le point \(A'\)
Pour déterminer une équation cartésienne d’une perpendiculaire commune à \(\mathcal D\) et \(\mathcal D'\) :
On forme le vecteur \(\overrightarrow{v} = \overrightarrow{u} \wedge \overrightarrow{u}'\).
On forme une équation cartésienne \(ax+by+cz+d=0\) du plan \(\mathcal P\) passant par \(A\) et engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\). Ce plan contient \(\mathcal D\).
On forme une équation cartésienne \(a'x+b'y+c'z+d'=0\) du plan \(\mathcal P'\) passant par \(A\) et engendré par \(\overrightarrow{u}\) et \(\overrightarrow{v}\). Ce plan contient \(\mathcal D\).
L’intersection de \(\mathcal P\) et de \(\mathcal P'\) est une droite dirigée par \(\overrightarrow{v}\). Par construction, cette droite est la perpendiculaire commune \(\Delta\) à \(\mathcal D\) et à \(\mathcal D'\). Un système d’équations cartésiennes pour \(\Delta\) est donc : \[\Delta: \begin{cases} ax+by+cz+d&=0\newlinea'x+b'y+c'z+d'&=0\end{cases}.\]
(Distance entre deux droites non parallèles). Soient \(\mathscr D\) et \(\mathscr D'\) deux droites non parallèles. Soient \(\Delta\) la perpendiculaire commune à ces deux droites, \(H\) le point d’intersection de \(\Delta\) avec \(\mathscr D\) et \(H'\) le point d’intersection de \(\Delta\) avec \(\mathscr D'\). Pour tout points \(M\) de \(\mathscr D\) et \(M'\) de \(\mathscr D'\), on a : \[d\left(H,H'\right) \leqslant d\left(M,M'\right)\] avec égalité si et seulement si \(H=M\) et \(H'=M'\). La distance \(d\left(H,H'\right)\) est appelée distance de \(\mathscr D\) à \(\mathscr D'\) et se note \(d\left(\mathscr D,\mathscr D'\right)\).
(1). \(\overrightarrow{MH}\) dirige \(\mathscr D\) et \(\overrightarrow{H'M'}\) dirige \(\mathscr D'\). Ces deux vecteurs sont donc orthogonaux à \(\overrightarrow{HH'}\). D’après le théorème de Pythagore, on a : \[\left\|\overrightarrow{MM'}\right\|^2 = \left\|\overrightarrow{MH} + \overrightarrow{H'M'}\right\|^2 +
\left\|\overrightarrow{HH'}\right\|^2.\] Il vient alors \(MM'\geqslant HH'\) et on a égalité si et seulement si \(\left\|\overrightarrow{MH} + \overrightarrow{H'M'}\right\|=0\), c’est-à-dire si et seulement si \(\overrightarrow{MH} +
\overrightarrow{H'M'}=\overrightarrow{0}\) ce qui équivaut à \(H=M\) et \(H'=M'\).
(Calcul de la distance entre deux droites non parallèles). Soient \(\mathscr D\) et \(\mathscr D'\) deux droites non parallèles de vecteurs directeurs respectifs \(\overrightarrow{u}\) et \(\overrightarrow{u}'\), passant respectivement par les points \(M\) et \(M'\). On a : \[\boxed{d\left(\mathscr D,\mathscr D'\right) = \dfrac{ \left| \mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u}',\overrightarrow{MM'}\right) \right| }{ \left\| \overrightarrow{u} \wedge \overrightarrow{u}' \right\| }}\]
(1). Soit \(\Delta\) la perpendiculaire commune aux deux droites \(\mathscr D\) et \(\mathscr D'\). Comme précédemment notons \(H\) le point formant l’intersection de \(\mathscr D\) et \(\Delta\), ainsi que \(H'\) le point formant l’intersection de \(\mathscr D'\) et \(\Delta\). On a \(d\left(\mathscr D,\mathscr
D'\right)=HH' = \left\|\overrightarrow{HH'}\right\|\). Les vecteurs \(\overrightarrow{u} \wedge \overrightarrow{u}'\) et \(\overrightarrow{HH'}\) sont colinéaires donc \[\left|\left(\overrightarrow{u} \wedge \overrightarrow{u}'\right) . \overrightarrow{HH'}\right| = \left\|\overrightarrow{u}
\wedge \overrightarrow{u}'\right\| \left\|\overrightarrow{HH'}\right\|.\] Par conséquent \[HH'= \dfrac{\left|\left(\overrightarrow{u}
\wedge \overrightarrow{u}'\right) . \overrightarrow{HH'}\right|}{\left\|\overrightarrow{u} \wedge \overrightarrow{u}'\right\|} =
\dfrac{\left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u}',\overrightarrow{HH'}\right)\right|}{\left\|\overrightarrow{u} \wedge \overrightarrow{u}'\right\|}\] On a de plus \[\begin{aligned}
\left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u}',\overrightarrow{MM'}\right)\right|&=& \left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u}',\overrightarrow{MH}+\overrightarrow{HH'}+\overrightarrow{H'M'}\right)\right|\\
&=& \left|\mathop{\rm det}\left(\overrightarrow{u},\overrightarrow{u}',\overrightarrow{HH'}\right)\right|
\textrm{ car $\overrightarrow{u}$ et $\overrightarrow{MH}$ ainsi que $\overrightarrow{u}'$ et $\overrightarrow{H'M'}$ sont
colinéaires}\\
&=&\left|\left(\overrightarrow{u} \wedge \overrightarrow{u}'\right) . \overrightarrow{HH'}\right| \textrm{ par définition du produit mixte}\newline
&=& \left\|\overrightarrow{u} \wedge \overrightarrow{u}'\right\|
\left\|\overrightarrow{HH'}\right\| \textrm{ car les vecteurs $\overrightarrow{u} \wedge \overrightarrow{u}'$ et $\overrightarrow{HH'}$
sont colinéaires}\end{aligned}\] d’où l’égalité.
Sphères
Généralités
(Sphère). Soient \(A\) un point de l’espace et \(R\in13 sqrt _+^*\) un réel positif non nul. On appelle sphère de rayon \(R\) et de centre \(A\) l’ensemble, noté \(\mathscr
S\left(A,R\right)\) des points de l’espace situés à une distance \(R\) de \(A\) : \[\mathscr S\left(A,R\right) = \left\{ M\in\mathscr E ~|~ AM=R\right\}\]
L’ensemble des points \(M\) de l’espace vérifiant \[\overrightarrow{MA} \cdot \overrightarrow{MB} = 0\] est la sphère de diamètre \(\left[AB\right]\).
(1). Soit \(I\) le milieu de \(\left[AB\right]\). Soit \(M\in \mathscr E\). On a : \[\begin{aligned}
\overrightarrow{MA} \cdot \overrightarrow{MB} = 0
\Longleftrightarrow\left(\overrightarrow{MI} + \overrightarrow{IA}\right).\left(\overrightarrow{MI} + \overrightarrow{IB}\right)=0
\Longleftrightarrow\left\|\overrightarrow{MI}\right\|^2 -\overrightarrow{IA}.\overrightarrow{IB}=0
\Longleftrightarrow IM = IA\end{aligned}\]
(Équation cartésienne d’une sphère).
Soit \(\mathscr R\) un repère orthonormal de l’espace. La sphère de centre \(A\left(a,b,c\right)\) et de rayon \(R\in13 sqrt _+^*\) admet comme équation cartésienne : \[\boxed{\left(x-a\right)^2+\left(y-b\right)^2+ \left(z-c\right)^2 - R^2=0}\]
Il suffit d’écrire que : \(M\left(x,y,z\right)\in\mathscr S \Longleftrightarrow\left\|\overrightarrow{AM}\right\|^2=R^2\).
Sphères et plans
(Position d’un plan par rapport à une sphère). Soit \(\mathscr S\) une sphère de centre \(A\) et de rayon \(R\in13 sqrt _+^*\). Soient \(\mathscr P\) un plan de l’espace et \(H\) le projeté orthogonal de \(A\) sur \(\mathscr P\).
Si \(d\left(A,\mathscr P\right)>R\) alors \(\mathscr P\cap \mathscr S = \varnothing\).
Si \(d\left(A,\mathscr P\right)=R\) alors \(\mathscr P\cap \mathscr S = \left\{H\right\}\).
Si \(d\left(A,\mathscr P\right)<R\) alors \(\mathscr P\cap \mathscr S\) est le cercle de centre \(H\) et de rayon \(\sqrt{R^2 - d^2\left(A,\mathscr P\right) }\).
Soit \(M\in\mathscr P\). Par application du théorème de Pythagore, \(d\left(A,M\right)^2 = d\left(A,H\right)^2 + d\left(H,M\right)^2= d\left(A,\mathscr P\right)^2 + d\left(H,M\right)^2\). Par conséquent, \(M\in\mathscr S\) si et seulement si \(R^2=d\left(A,M\right)^2 =d\left(A,\mathscr
P\right)^2 + d\left(H,M\right)^2\).
Sphères et droite
Soit \(\mathscr R\left(O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)\) un repère orthonormal de l’espace.
On étudie dans ce paragraphe l’intersection entre une sphère \(\mathscr S\) et une droite \(\mathscr D\). Afin de simplifier le problème, on peut supposer que \(\mathscr D\) est dirigée par le vecteur \(\overrightarrow{k}\), que \(O\) est le centre de \(\mathscr S\). Une équation cartésienne de \(\mathscr S\) dans \(\mathscr R\) est alors : \(x^2+y^2+z^2=R^2\) où \(R\in13 sqrt _+^*\) est le rayon de \(\mathscr S\).
\(\mathscr D\) coupe le plan passant par \(O\) et dirigé par les vecteurs \(\overrightarrow{i}\) et \(\overrightarrow{j}\) en le point \(A\left(a,b,0\right)\). Elle est donc paramétrée par : \(\begin{cases} x=a\\ y=b\newline z=t \end{cases}.\)
(Position d’une droite par rapport à une sphère). Posons \(d=d\left(O,\mathscr D\right)\). On a :
Si \(d>R\) alors \(\mathscr D\) et \(\mathscr S\) ont une intersection vide.
Si \(d=R\) alors \(\mathscr D\) et \(\mathscr S\) ont un point commun et un seul. On dit que la droite est tangente à la sphère.
Si \(d<R\) alors \(\mathscr D\) et \(\mathscr S\) ont exactement deux points en commun.
On a : \(M\left(x,y,z\right)\in \mathscr D \cap \mathscr S \Longleftrightarrow x=a, x=b, z=t \quad \textrm{ et} \quad
x^2+y^2+z^2=R^2 \Longleftrightarrow x=a, x=b, z=t \quad \textrm{ et} \quad a^2+b^2+t^2=R^2\). Comme \(d=a^2+b^2\), on a : \(M\left(x,y,z\right)\in \mathscr D \Longleftrightarrow t^2 = R^2 - d^2\).
En résumé
Il convient d’avoir bien compris :
l’utilité du produit scalaire
l’utilité du déterminant
l’utilité du produit mixte
et les différentes techniques pour les calculer.
Il faut savoir calculer rapidement et sans hésitation
l’équation cartésienne et de l’équation paramétrée d’un plan
l’équation cartésienne et de l’équation paramétrée d’une droite
l’équation cartésienne d’une sphère
Il faut savoir retrouver rapidement aussi les formules de changements de coordonnées sphériques et cylindriques. Elles seront utilisées à la fois en mathématiques et en physique.
Les différentes formules pour calculer la distance d’un point à un plan, d’un point à une droite, entre deux droites, ou le volume d’un parallélépipède doivent être bien connues.
Bibliographie
Barre utilisateur
[ID: 59] [Date de publication: 31 octobre 2021 20:00] [Catégorie(s): Le cours de SUP ] [ Nombre commentaires: 0] [nombre d'éditeurs: 1 ] [Editeur(s): Emmanuel Vieillard-Baron ] [nombre d'auteurs: 3 ] [Auteur(s): Emmanuel Vieillard-Baron Alain Soyeur François Capaces ]Commentaires sur le cours
Documents à télécharger
L'article complet