Diffraction, Fraunhofer et Young
Bonjour,
j'ai essayé de me plonger dans les maths de l'histoire des fentes de Young, pour voir ce qui se cachait derrière les histoires vulgarisées que j'avais lues.
Je suis tombé sur un truc qui me semble bizarre.
Voici l'image où j'ai quelque chose à objecter :
Bon, alors. Supposons que ce soit des photons (je ne sais pas si ça change quelque chose).
D'après ce que j'ai compris, si $f$ est la fonction représentant l'ouverture par laquelle passent les photons ($\textbf{1}_{[-1,1]}$ représenterait une fente avec ouverture complète entre $-1$ et $1$, et $x \mapsto e^{-x^2}$ représenterait une "fente continue", qui serait une fente par laquelle une certaine portion de la lumière passe, en chaque point, plutôt que passer/pas passer), alors la fonction d'onde représentant la lumière touchant en un point de coordonnée $\xi$ sur l'écran (situé à distance $D$) est (proportionnelle à) :
$\int^{+\infty}_{-\infty} f(x)\frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} dx$ où $\alpha$ est un réel correpondant à certaines propriétés de la lumière qui passe (mais j'ai pas trop compris et je crois qu'on s'en moque ici) EDIT : J'avais oublié de mettre $f$, merci Calli !
Cette intégrale est considérée comme trop compliquée ! On fait donc l'approximation de Fraunhofer, qui consiste à considérer que les fentes sont dans une région toute petite comparée à la distance entre les fentes et l'écran (le nombre $D$).
Ainsi, $\sqrt{D^2 + (x-\xi)^2} \simeq D + \frac{(x-\xi)^2}{2D}$, on remplace ça partout, et en faisant une autre simplification, on se ramène à la transformée de Fourier de $f$ évaluée en $\xi$.
Mes questions sont les suivantes :
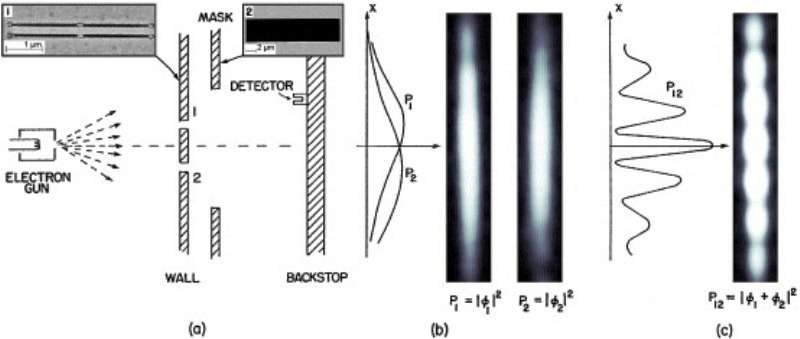
1) Revenons à l'histoire où on a deux "vraies" fentes. Sous l'hypothèse de l'approximation de Fraunhofer, les fentes sont... "infinitésimales". Et donc, les deux taches qu'on voit sur l'écran (correspondant chaque à ce qu'on observe quand une des fentes est fermée) qui sont représentées par $P_1$ et $P_2$ sur l'image... sont égales !
D'ailleurs, la transformée de Fourier voit bien ça : les deux fentes sont les mêmes, à translation près ; et l'effet d'une translation, en Fourier, c'est un décalage de phase (qui ne change donc pas l'intensité). Donc, si on fait l'approximation de Fraunhofer, le dessin est trompeur, car il montre un $P_1$ et un $P_2$ qui sont bien distincts (mais qui se chevauchent un peu). D'ailleurs, c'est ce qu'on voit sur les "photos" : les deux taches ont l'air à peu près identiques (enfin, en tout cas, elles ont l'air centrées au même endroit).
Est-ce que vous êtes d'accord ? Est-ce que l'analyse peut être poussée plus loin sans faire l'approximation de Fraunhofer ?
2) Est-ce que vous connaissez une référence mathématiquement accessible où on pourrait trouver des "démonstrations", des calculs exacts, de tout ça ? Par exemple, la formule $\int^{+\infty}_{-\infty} \frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} dx$, je crois que je saurais la justifier un peu avec les mains. Mais bon, j'aimerais comprendre qui est $\alpha$, je voudrais aller dans les détails.
j'ai essayé de me plonger dans les maths de l'histoire des fentes de Young, pour voir ce qui se cachait derrière les histoires vulgarisées que j'avais lues.
Je suis tombé sur un truc qui me semble bizarre.
Voici l'image où j'ai quelque chose à objecter :

Bon, alors. Supposons que ce soit des photons (je ne sais pas si ça change quelque chose).
D'après ce que j'ai compris, si $f$ est la fonction représentant l'ouverture par laquelle passent les photons ($\textbf{1}_{[-1,1]}$ représenterait une fente avec ouverture complète entre $-1$ et $1$, et $x \mapsto e^{-x^2}$ représenterait une "fente continue", qui serait une fente par laquelle une certaine portion de la lumière passe, en chaque point, plutôt que passer/pas passer), alors la fonction d'onde représentant la lumière touchant en un point de coordonnée $\xi$ sur l'écran (situé à distance $D$) est (proportionnelle à) :
$\int^{+\infty}_{-\infty} f(x)\frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} dx$ où $\alpha$ est un réel correpondant à certaines propriétés de la lumière qui passe (mais j'ai pas trop compris et je crois qu'on s'en moque ici) EDIT : J'avais oublié de mettre $f$, merci Calli !
Cette intégrale est considérée comme trop compliquée ! On fait donc l'approximation de Fraunhofer, qui consiste à considérer que les fentes sont dans une région toute petite comparée à la distance entre les fentes et l'écran (le nombre $D$).
Ainsi, $\sqrt{D^2 + (x-\xi)^2} \simeq D + \frac{(x-\xi)^2}{2D}$, on remplace ça partout, et en faisant une autre simplification, on se ramène à la transformée de Fourier de $f$ évaluée en $\xi$.
Mes questions sont les suivantes :
1) Revenons à l'histoire où on a deux "vraies" fentes. Sous l'hypothèse de l'approximation de Fraunhofer, les fentes sont... "infinitésimales". Et donc, les deux taches qu'on voit sur l'écran (correspondant chaque à ce qu'on observe quand une des fentes est fermée) qui sont représentées par $P_1$ et $P_2$ sur l'image... sont égales !
D'ailleurs, la transformée de Fourier voit bien ça : les deux fentes sont les mêmes, à translation près ; et l'effet d'une translation, en Fourier, c'est un décalage de phase (qui ne change donc pas l'intensité). Donc, si on fait l'approximation de Fraunhofer, le dessin est trompeur, car il montre un $P_1$ et un $P_2$ qui sont bien distincts (mais qui se chevauchent un peu). D'ailleurs, c'est ce qu'on voit sur les "photos" : les deux taches ont l'air à peu près identiques (enfin, en tout cas, elles ont l'air centrées au même endroit).
Est-ce que vous êtes d'accord ? Est-ce que l'analyse peut être poussée plus loin sans faire l'approximation de Fraunhofer ?
2) Est-ce que vous connaissez une référence mathématiquement accessible où on pourrait trouver des "démonstrations", des calculs exacts, de tout ça ? Par exemple, la formule $\int^{+\infty}_{-\infty} \frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} dx$, je crois que je saurais la justifier un peu avec les mains. Mais bon, j'aimerais comprendre qui est $\alpha$, je voudrais aller dans les détails.
Réponses
-
Bonjour,
Je n'ai pas bien compris le $\int^{+\infty}_{-\infty} \frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} dx$. Il n'est pas censé y avoir du $f$ là-dedans ? J'aurais plutôt vu quelque chose comme $\int^{+\infty}_{-\infty} \frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} f(x) \,dx$.
Et des fentes "infinitésimales", ça parle de leur largeur à chacune ou de la distance entre les deux fentes ?
Que les fentes aient des largeurs infinitésimales n'implique pas que $P_1=P_2$. -
@Calli : Oui, oui, j'ai oublié $f(x)$ dans l'intégrale :-D Je la rajoute.
Ce qui doit être infinitésimal, c'est la somme de la largeur des fentes et de la distance entre les fentes. En fait, "moralement" (je n'aime pas trop ce mot) c'est le diamètre du support de $f$ qui doit être petit devant $D$. -
Ok. Bon déjà, $\alpha$ c'est la pulsation spatiale de l'onde (je ne souviens plus si c'est vraiment ça le terme propre). Donc, en notant $\nu$ la fréquence de l'onde, $\alpha = 2\pi \frac\nu c$ avec $c$ la vitesse de la lumière.
Edit : On peut aussi écrire $\alpha = \frac{2\pi}\lambda$ avec $\lambda$ la longueur d'onde. -
J'ai regardé un peu l'article Wikipédia parce que je ne connaissais pas "l'approximation de Fraunhofer". Du coup, je ne suis pas expert, mais je vais quand même donner mon avis :-D (c'est comme ça que les choses fonctionnent non ?).
https://fr.wikipedia.org/wiki/Diffraction_de_FraunhoferGeorges a écrit:1) Revenons à l'histoire où on a deux "vraies" fentes. Sous l'hypothèse de l'approximation de Fraunhofer, les fentes sont... "infinitésimales". Et donc, les deux taches qu'on voit sur l'écran (correspondant chaque à ce qu'on observe quand une des fentes est fermée) qui sont représentées par $P_1$ et $P_2$ sur l'image... sont égales !
D'après Docteur Wikipédia, l'approximation de Fraunhofer est vérifiée quand les rayons lumineux incidents sont parallèles avant l'obstacle (onde plane) et quand l'écran est situé à l'infini ($D\to\infty$). En pratique, ça peut s'obtenir simplement avec des lentilles convergentes (je peux détailler comment si besoin). Mais $D$ grand n'est pas équivalent à $a$ petit (j'appelle $a$ le diamètre du support de $f$) car il y a un troisième paramètre de longueur : la longueur d'onde $\lambda$.
Si on a $a\ll \lambda, D$, alors la source lumineuse sera ponctuelle (les deux fentes sont confondues en une seule fente) donc on n'a plus d'interférences ! Et effectivement, $P_1$ et $P_2$ sont confondus. Dans le calcul avec l'intégrale, ça se traduit par la convergence $f(x)\,{\rm d}x$ vers un Dirac en 0, donc l'intensité lumineuse est juste $\Big| \int^{+\infty}_{-\infty} f(x)\frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} dx \Big| = \frac{1}{\sqrt{D^2 +\xi^2}} $.
Mais si $D\gg a,\lambda$, alors $a$ n'est pas forcément infinitésimal, c'est juste que l'écran est loin. Donc on a bien des interférences (ouf). Et $P_1$ et $P_2$ sont bien non confondus et décalés d'environ $a$ l'un de l'autre. Du point de vue calculs, on peut utiliser le développement asymptotique de $\sqrt{D^2 + (x-\xi)^2}$ dont tu parlais et il faut probablement multiplier $\int^{+\infty}_{-\infty} f(x)\frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} dx$ par $D$ pour éviter de se retrouver avec un truc qui tend vers 0 quand $D\to\infty$.Georges a écrit:D'ailleurs, c'est ce qu'on voit sur les "photos" : les deux taches ont l'air à peu près identiques (enfin, en tout cas, elles ont l'air centrées au même endroit).
À mon avis c'est juste que les fentes sont trop proches (mettons $a <$ 1 cm, voire $a<$ 5 mm) par rapport à la largeur de la figure (mettons 10 cm) pour que le décalage soit visible en pratique. En revanche l'onde voit les différences de marche à l'échelle de $\lambda $ ($<$ 1 mm pour la lumière visible), donc elle perçoit très bien le décalage ! -
Oui, oui, bien entendu, ton avis m'intéresse !
Bon il est tard et je lirai demain, mais je ne vois pas pourquoi (formellement parlant) ce que tu dis contrevient à la deuxième facette de mon argument : si le schmilblick sur l'écran est la transformée de Fourier de l'ouverture, si on note $\textbf{1}_{[-b,-a]}$ la première fente et $\textbf{1}_{[a,b]}$ la deuxième fente, alors les transformées de Fourier de ces deux machins sont identiques en module !
Et la transformée de Fourier de leur somme va bien montrer les interférences.
Bon j'avoue que comme je pigeais pas qui était $\alpha$, j'ai fait comme s'il n'y avait rien à comprendre là-dedans, mais comme ce $\alpha$ contient le $\lambda$...
Pour l'histoire des lentilles, ben, je veux bien que tu détailles mais je ne suis pas sûr de comprendre ! -
Le montage avec les lentilles est le suivant. Il faut placer la source lumineuse et l'écran aux foyers (objet, resp. image) des lentilles (1, resp. 2) comme indiqué. Parce que l'image par une lentille convergente d'un objet présent au foyer objet est à l'infini (rayons parallèles), et l'image d'un objet (virtuel) présent à l'infini côté droit est en le foyer image.
-
(Je rajoute que $D$ grand n'est pas équivalent à $a$ petit car en pratique $\lambda <a$. Donc en faisant $a\ll \lambda,D$, on renverse carrément cette inégalité et c'est ça qui détruit les interférences. Je voulais l'écrire et j'ai oublié.)
-
J'ai édité mon message sur les lentilles parce qu'il me semble que j'avais fait une erreur.
-
Je n'ai pas répondu à ce que tu disais sur Fourier, parce que je l'ai sauté en fait. 8-)
Tu n'as pas précisé comment tu arrives à du Fourier, est-ce que c'est ainsi ? :$$
\begin{eqnarray*}
\Big| \int_{-\infty}^\infty \frac{1}{\sqrt{D^2 + (x-\xi)^2}} e^{i\alpha \sqrt{D^2 + (x-\xi)^2}} f(x) \,{\rm d}x \Big|
&\underset{D\to\infty}\approx& \Big| \int_{-\infty}^\infty \frac1D e^{i\alpha (D + \frac{(x-\xi)^2}{2D})} f(x) \,{\rm d}x \Big| \\
&=& \frac1D \Big| \int_{-a}^a e^{\frac{i\alpha}{2D} (x^2-2x\xi)} f(x) \,{\rm d}x \Big| \\[1mm]
&\approx& \frac1D \Big| \int_{-a}^a e^{-\frac{i\alpha}{D} x\xi} f(x) \,{\rm d}x \Big| \\[1mm]
&=& \frac1D \Big| \hat f \Big(\frac{\alpha\xi}{D}\Big) \Big|
\end{eqnarray*}
$$ où l'approximation $ x^2 \approx 0$ (en fait $x^2 \ll x\xi $) pour $x\in[-a,a]$ est valable quand $\xi \gg a$ (de toute façon, vu la taille des taches d'interférences qu'on va obtenir sur un écran aussi loin, il ne faut pas prendre $\xi$ trop petit).
Du coup, effectivement, la seule différence entre les termes donnés par chaque fente est une différence de phase. C'est dû à l'approximation $1/\sqrt{D^2 + (x-\xi)^2}\approx 1/D$. En effet, c'est ce facteur d'origine géométrique qui contrôlait la différence d'intensité de la lumière provenant de chaque fente en fonction de $\xi$ et qui faisait que l'intensité de la lumière venant de la fente de gauche est plus forte en face de la fente de gauche (tache $P_1$ décalée vers la gauche). Mais, par diffraction, la lumière se propage après les fentes dans plusieurs directions, ce qui fait diminuer l'intensité lumineuse avec la distance aux fentes. Donc lorsque $D\gg a$, les distances entre un point de l'écran et chacune des fentes sont quasiment les mêmes, d'où les taches $P_1$ et $P_2$ deviennent identiques. Dans le calcul, on n'a gardé que le facteur de différence de marche (l'exponentielle) qui induit une différence de phase.
Bref, blablabla... je suis d'accord avec toi sur l'interprétation de Fourier.
Cependant, en pratique, l'écran n'est pas vraiment à l'infini, il est juste derrière une lentille. Au niveau différence de marche, ça ne change rien, mais ça change l'intensité. Le facteur $1/\sqrt{D^2 + (x-\xi)^2} $ n'est plus pertinent car la distance réelle aux fentes est beaucoup plus petite que $D$ ($D$ n'est plus que la distance effective entre l'écran et les fentes du point de vue optique) et la lumière ne se disperse pas autant. Il faudrait remplacer ce facteur par une fonction grosso modo en cloche avec un maximum en $x-\xi=0$ (je ne connais pas son expression exacte). Et alors, les profils $P_1$ et $P_2$ ne sont pas confondus, mais bien décalés de $a$ (ce qui ne veut pas dire que les deux taches sont facilement distinguables à l'œil nu, comme je le disais dans un précédent message). Ça réhabilite l'image que tu critiquais. (Par contre $P_1$ et $P_2$ sont inversés parce que la lentille met les images tête bêche. :-D)
Donc dans le cas d'un montage pratique avec lentilles, on ne peut pas remplacer le facteur $1/\sqrt{D^2 + (x-\xi)^2} $ par $1/D$ car la dépendance en $\xi $ ne disparaît pas. Donc on ne peut plus faire l'approximation par la transformée de Fourier de façon exacte (enfin, "exacte" ^^... comme une bonne approximation). Est-ce que c'est un problème ? Pas tellement. Ça ne change pas la prédiction des interférences et ça ne condamne pas le calcul de la largeur des taches d'interférences sur l'écran. En revanche, l'intensité venant des deux fentes en un point de l'écran étant différentes, la qualité des interférences sera moindre que ce qu'on prédisait avec Fourier... mais comme $a$ est petit, ça ne devrait pas se voir à l'œil nu. -
Merci pour tous les détails. Je n'ai pas compris grand chose sur les lentilles, mais passons, ce n'est probablement pas le plus intéressant (de même, je crois que tu proposes de poursuivre le calcul dans le cas de lentilles mais j'ai des ambitions plutôt modestes).
J'ai refait les calculs plusieurs fois, et je suis un peu bloqué au niveau de choisir mes asymptotiques. Je crois que je vais faire plusieurs calculs différents :
- un où l'ouverture est à support dans $[-\epsilon,\epsilon]$ (une fente au milieu) ;
- un où l'ouverture est à support dans $[-a -\epsilon,-a+\epsilon]$ (une fente sur la gauche) ;
- un où l'ouverture est à support dans $[-a-\epsilon,-a+\epsilon]\cup [a-\epsilon,a+\epsilon]$ (deux fentes).
En outre, pour voir ton histoire de $x^2 \ll x\xi$, je vais prendre $b_1,b_2$ et décréter que $\xi \in [-b_2,b_1]\cup [b_1,b_2]$, comme ça je verrai si à un moment, il faut bien prendre $a \ll b_1$.
En plus, pour que le terme final de ton dernier message ne soit pas trivial, il faudrait que $\frac{\alpha}{D} \simeq 1$, c'est-à-dire que $\lambda D \simeq 1$, non ? -
Non, je ne proposais pas de continuer les calcul pour les lentilles car ça m'a l'air trop compliqué.
C'est légitime de faire les calculs pour $\xi\gg a\geqslant x$ car l'échelle de grandeur intéressante pour $\xi$ est celle de l'interfrange sur l'écran, or celle-ci est proportionnelle à $D$ et $D\to\infty$.
C'est quoi le "terme final de ton dernier message" dont tu parles ?
D'ailleurs, je ne sais toujours pas de quelle manière tu étais tombé sur la transformée de Fourier toi. -
Ton $\hat{f}(\frac{\alpha}{D}\xi)$. Pour que ça ne soit pas trivial, ce serait bien que $\frac{\alpha}{D}$ soit proche de $1$, non ? Ah, je crois que j'ai compris : tu dis qu'il est plus pertinent de demander que $\frac{\xi}{D}$ ne soit pas trop petit ?
Pour cette histoire de transformée de Fourier, c'est effectivement comme tu as dit ! C'est le "calcul" habituellement proposé par les textes physiciens, pour autant que je puisse en juger.
J'avais plusieurs envies/problèmes : d'une part, arriver à rendre le calcul rigoureux et précis pour arriver à Fourier ; d'autre part, savoir si, physiquement parlant, pour l'interprétation, pour l'application à l'expérience, c'était vraiment Fourier, l'approximation qu'il fallait faire. Ma seule raison "à moi" de voir Fourier comme un point de passage dans le chemin que je me suis tracé, c'est parce que ça avait l'air de simplifier les calculs. Mais comme tu dis qu'il ne faut pas simplifier $\frac{1}{\sqrt{D^2 + (\xi - x)^2}}$ en $\frac{1}{D}$, je me dis que Fourier, c'est peut-être un pas d'approximation de trop.
Quand j'ai du temps libre, je m'y remets et je tâcherai de mettre les choses à plat. -
Pour que ça ne soit pas trivial, ce serait bien que $\frac{\alpha}{D}$ soit proche de $1$, non ?
Non, jamais de la vie, pour une bonne raison : la dimension de $\frac{\alpha}{D}$ c'est une longueur puissance $-2$. Pour le comparer à 1, il faudrait que ce soit sans dimension.
L'ordre de grandeur pertinent pour $f$ est $a$ (c'est la seule longueur qui a un lien avec $f$). Comme $\hat f$ prend en argument des inverses de longueurs, l'ordre de grandeur pertinent pour $\hat f$ ne peut pas être autre chose que $\frac1a$. Parmi $\alpha$, $D$ et $\xi$, les ordres de grandeurs de $\alpha$ et $D$ sont fixés (ce sont des données) et $\xi$ est libre. Donc il faut regarder ce qui se passe pour certains ordres de grandeur de $\xi$ dépendant de $(a,\alpha,D)$ qui seront plus pertinents. Du coup, ce qui est pertinent pour regarder $\hat f(\frac{\alpha\xi}D)$ c'est $\frac1\alpha \asymp \frac{\alpha\xi}D$ (j'utilise $\asymp$ pour signaler un ordre de grandeur comparable, pour ne pas confondre avec $\approx$ qui est plus précis). C'est-à-dire $\xi \asymp \frac{D}{\alpha \,a}\asymp\frac{\lambda D}a$. Et devine quoi ? $\frac{\lambda D}a$ s'avère être exactement l'interfrange !
Maintenant j'espère que tu comprends mieux ce que je disais quand je parlais "d'ordre de grandeur pertinent pour $\xi$". Si $\xi \ll\frac{\lambda D}a$, alors on est en plein milieu de la tache centrale et on est trop zoomé pour voir les interférences. Et si $\xi \gg\frac{\lambda D}a$, on est à une échelle beaucoup plus grande que l'interfrange, donc on ne distingue plus les franges d'interférences.Ah, je crois que j'ai compris : tu dis qu'il est plus pertinent de demander que $\frac{\xi}{D}$ ne soit pas trop petit ?
Oui (tu). Quand $D\gg a$, les rayons se propagent en gros en rayonnant depuis quasiment un même point, donc $\frac{\xi}D$ est la grandeur pertinente pour les positions sur l'écran, plus que $\xi$. -
Georges a écrit:Mais comme tu dis qu'il ne faut pas simplifier $\frac{1}{\sqrt{D^2 + (\xi - x)^2}}$ en $\frac{1}{D}$, je me dis que Fourier, c'est peut-être un pas d'approximation de trop.
Non mais en vrai ça va à mon avis comme approximation de remplacer $\frac{1}{\sqrt{D^2 + (\xi - x)^2}}$ par une constante. (Peut-être pas $D$, mais plutôt la distance fentes-lentille 2, parce qu'après la lentille 2, les rayons ne s'écartent plus, mais aucune importe car on écrivait l'intensité à une constante près.) Je voulais surtout dire qu'on ne pouvais pas critiquer l'image que tu as jointe pour avoir dessiné $P_1$ et $P_2$ décalés car ils sont vraiment un peu décalés, même si ça se voit peu.Calli a écrit:Donc on ne peut plus faire l'approximation par la transformée de Fourier de façon exacte [...]. Est-ce que c'est un problème ? Pas tellement. Ça ne change pas la prédiction des interférences et ça ne condamne pas le calcul de la largeur des taches d'interférences sur l'écran. En revanche, l'intensité venant des deux fentes en un point de l'écran étant différentes, la qualité des interférences sera moindre que ce qu'on prédisait avec Fourier... mais comme $a$ est petit, ça ne devrait pas se voir à l'œil nu.
J'avais peut-être un peu trop insisté sur les défauts de l'approximation faite parce que ça te faisait râler sur l'image ("le dessin est trompeur"). Mais je pense qu'en pratique elle est satisfaisante. -
Oups oups oups en effet, je plaide coupable pour l'analyse dimensionnelle, ça ne veut effectivement rien dire qu'une distance $^-2$ est proche de $1$... Dans une autre vie, je prendrai des UE de physique à la fac...
Eh bien... Je suis au moins content parce que tu m'as appris plein de trucs. Tant qu'on y est, quand tu dis que tu distingues des symboles pour "le même ordre" parce qu'il y en a un qui est plus précis, tu veux dire quoi par là ? Ces symboles ont une autre définition que celle intuitive :-D ? -
Le symbole $\asymp$ n'a rien d'officiel (je ne l'ai jamais vu en physique, en fait). C'est juste que j'avais déjà utilisé $\approx$ pour dire que deux nombres sont presque égaux. Par exemple $1\approx 1{,}01$ mais $1\not\approx 2$. Donc j'ai préféré utiliser un autre symbole pour signaler un ordre de grandeur comparable. Par exemple $1\asymp 5$ mais $1\not\asymp 10^3$. Du coup $a\approx b\Rightarrow a\asymp b$.
Au passage, moi j'ai appris qu'on pouvait voir les figures d'interférences sur l'écran comme la transformée de Fourier de l'ouverture. Je ne le savais pas.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres


