Möbius, projectif, bouteille de Klein , etc.
dans Algèbre
Bonjour à tous, je vais tenter de combler ma terrible inculture avec ce fil.
Quand on a découvert et investigué déterminant, produit scalaire et cie, on a un peu utilisé des langages changeant, mais en 2020, ça va les choses sont claires.
Je me disais ce matin que le déterminant (en dim2) de $(a,b)$ est l'objet abstrait obtenu comme suit.
On calcule $(a+b)\otimes (a+b)$, on obtient $a\otimes a + a\otimes b + b\otimes a + b\otimes b$, puis on dit que comme il est plat (on multiplie un truc par lui-même, il se doit de valoir $0$, ainsi que $a\otimes a$ et $b\otimes b$).
Comme on veut que ça représente le volume, "in some sense", on prend $a\otimes b$ OU $b\otimes a$, mais on ne sait pas trop au juste lequel prendre (un peu comme l'hésitation entre $i$ et $(-i)$ qui n'a pas beaucoup de sens.
Par contre, d'après ce qui précède, on a que $a\otimes b$ doit être vu comme $-(b\otimes a)$ modulo tout ce qu'on a jeté en l'accusant d'être plat.
Ce qui fait qu'on a des volumes ORIENTES!! (au moins si on veut "du Chasles-aires")
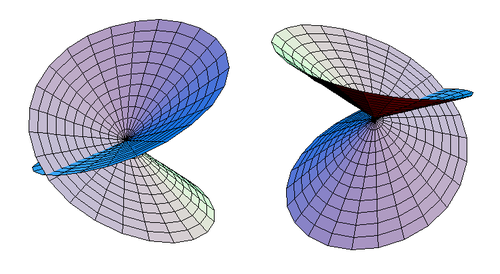
Or sur le ruban de Möbius, sur la bouteille de Klein, c'est pas évident de calculer un volume orienté avec le quel tout le monde sera d'accord, non ?
Que se passe-t-il ? Y a-t-il des gens qui se sont amusés à regarder ça de près ?
Et enfin question "autre" : prenons un disque et identifions ses points diamétralement opposés 2 à 2. Là encore ça donne un truc non orientable (les gauchers deviennent droitiers en franchissant les téléportages). C'est difféomorphe à quoi ? À la bouteille de Klein ? Et sinon, y a-t-il des sites dessins collectionnant les surfaces et volumes non orientables ?
Même question pour plan projectif ?
Merci d'avance ?
Quand on a découvert et investigué déterminant, produit scalaire et cie, on a un peu utilisé des langages changeant, mais en 2020, ça va les choses sont claires.
Je me disais ce matin que le déterminant (en dim2) de $(a,b)$ est l'objet abstrait obtenu comme suit.
On calcule $(a+b)\otimes (a+b)$, on obtient $a\otimes a + a\otimes b + b\otimes a + b\otimes b$, puis on dit que comme il est plat (on multiplie un truc par lui-même, il se doit de valoir $0$, ainsi que $a\otimes a$ et $b\otimes b$).
Comme on veut que ça représente le volume, "in some sense", on prend $a\otimes b$ OU $b\otimes a$, mais on ne sait pas trop au juste lequel prendre (un peu comme l'hésitation entre $i$ et $(-i)$ qui n'a pas beaucoup de sens.
Par contre, d'après ce qui précède, on a que $a\otimes b$ doit être vu comme $-(b\otimes a)$ modulo tout ce qu'on a jeté en l'accusant d'être plat.
Ce qui fait qu'on a des volumes ORIENTES!! (au moins si on veut "du Chasles-aires")
Or sur le ruban de Möbius, sur la bouteille de Klein, c'est pas évident de calculer un volume orienté avec le quel tout le monde sera d'accord, non ?
Que se passe-t-il ? Y a-t-il des gens qui se sont amusés à regarder ça de près ?
Et enfin question "autre" : prenons un disque et identifions ses points diamétralement opposés 2 à 2. Là encore ça donne un truc non orientable (les gauchers deviennent droitiers en franchissant les téléportages). C'est difféomorphe à quoi ? À la bouteille de Klein ? Et sinon, y a-t-il des sites dessins collectionnant les surfaces et volumes non orientables ?
Même question pour plan projectif ?
Merci d'avance ?
Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
Réponses
-
Salut Christophe,
Tu as fait une petite erreur de calcul, le dernier terme dans ton développement est $b\otimes b$. Pour le reste, je ne peux malheureusement pas t'aider. -
Salut Christophe,
Tu définis le produit extérieur de deux modules sur un anneau commutatif comme le quotient du tensoriel par la relation $a \otimes b-b \otimes a$.
Tu notes $\wedge$ le produit sur le quotient. Après pour passer du local au global c'est la théorie des faisceaux donc ça dépend ce que tu veux faire exactement. La question que tu poses est l'objet du mémoire de Möbius perdu je crois primé à l'Académie des sciences.
Un disque dont tu as identifié le bord antipodalement c'est le plan projectif , le disque est un domaine fondamental de l'action sur la sphère (disque=hémisphère).
M. -
CC a écrit:prenons un disque et identifions ses points diamétralement opposés 2 à 2. Là encore ça donne un truc non orientable (les gauchers deviennent droitiers en franchissant les téléportages). C'est difféomorphe à quoi?
Je peux au moins répondre à ça. C'est le plan projectif réel, ce qui n'est pas trop difficile à se représenter (les points du bord sont les points de la droite à l'infini). -
Salut,
Poirot a nommé $\Bbb R P^2$ avant que j'aie le temps d'écrire, mais je peux néanmoins donner des images le représentant :
source : https://en.wikipedia.org/wiki/Real_projective_plane -
Mauricio
Le produit extérieur de deux modules sur un anneau commutatif, je n'en ai jamais entendu parler. Quelles sont tes références ? La mienne est : A.III Algèbres tensorielles, extérieures et symétriques de Bourbaki (écrit par Dieudonné, je crois). Je n'en pense pas que du bien (de ce chapitre A.IIII) mais comme certaines personnes ont cogité là-dedans, on aurait tort ne pas consulter ce sur quoi elles ont planché (ainsi que les diverses tentatives de Chevalley pour revoir certaines parties, notamment celles qui touchent à ``l'algèbre intérieure'').
L'algèbre extérieure $\bigwedge M$ d'un $A$-module $M$ est construite comme le quotient de l'algèbre tensorielle par l'idéal bilatère engendré par les $x \otimes x$ pour $x \in M$. Elle devient une algèbre graduée alternée (au sens de Bourbaki, en anglais skew commutative algebra) ce qui se mérite.
Certes le A.III de Bourbaki est en quelque sorte une usine à gaz. Mais pas de jugements hâtifs. Il faut une fois dans sa vie s'être battu avec les ``formules de type shuffle'' et voir comment Bourbaki a contourné le truc en introduisant le co-produit :
$$
\bigwedge M \mapsto \bigwedge M \otimes^{\rm gr.} \bigwedge M
$$Cela fait monter la mer mais trivialise les calculs. -
Je ne sais pas si c'est ta question, mais en effet sur une variété non orientable, il n'y a pas de "forme volume" (qui permet de définir l'intégration globalement etc. etc.).
En particulier pour les espaces projectifs en dimension paire (donc le plan et tous ceux au-dessus) tu vas effectivement avoir du mal.
Tu peux te sortir de la non orientabilité si tu joues avec la caractéristique $2$, monde magnifique dans lequel tout le monde est orientable.
(cela dit, je ne connais rien à la "géométrie différentielle en caractéristique $2$", je ne sais même pas si ça a un sens - en particulier, l'obstruction de base à définir un volume n'existe plus, mais est-ce qu'on peut pour autant définir un volume ? je ne sais pas...) -
Un immense merci à vous tous, je vais corriger la coquille signalée par Sylvain. C'est que de la balle tout ça!!
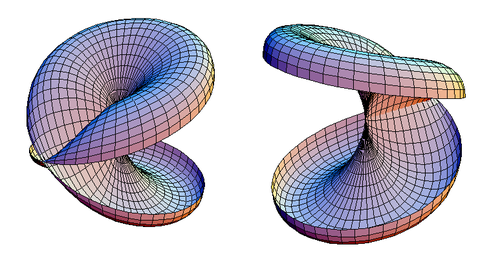
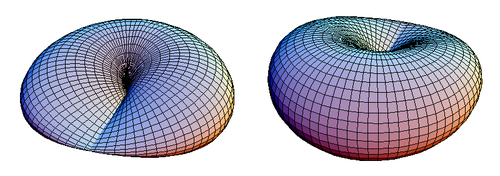
Tes deux premières photos, celles du haut Calli, elles sont là pour montrer AVANT RECOLLEMENT ce que seront les deux du bas, c'est ça?
@Mauricio et Claude, je n'ai pas le niveau pour m'envoyer de l'algèbre pointue, mais je dispose de mon "propre paradigme enfantin", consistant à "rendre nul ce que j'ai envie", pour créer des opérations et j'ai un gout pour voir les choses comme ça donc tant mieux. Par contre, la toute dernière formule de Claude m'échappe, mais quand je vois "gr" de toute façon, j'ai une certaine tendance à fuir à toute jambe (je ne sais pas si c'est très rationnel***)
*** j'ai un peu le préjugé (avecle mot gradué) que ce sont des machins définis sur des trucs différents, genre une distance par niveau etc, et là j'ai peur et je fuis.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
@Claude et Mauricio, j'ai souvent en tête les multiples "caprices" qui sont très fréquemment rappelés, avec
- le produit scalaire
- les deux produits qui définissent le produit dans $\C$
- le déterminant $2 \times 2$.
A chaque fois on jette quelque chose qu'on veut "nulle dans la philosophie étudiée", et c'est marrant de voir quoi.
Pour le volume, jeter les $x\otimes x$, c'est clair
Pour le "produit scalaire", jeter les $e_i\otimes e_j$ de la base aussi (volonté de rendre invisible à un quidam ce qui lui est orthogonal, très prisé dans le $\neq$ quantique
Mézalor, je n'ai jamais vraiment "fouillé" ce qui émergeait du produit complexe et si vous avez un discours sous la main ce serait intéressant.
$$ ((x_1,y_1),(x_2,y_2)) \longmapsto (x_1x_2-y_1y_2 , x_1y_2 + y_1x_2) $$
C'est marrant il n'y a pas un seul des deux qui rejoint l'un de ceux d'avant.
Si je transpose à du abstrait symbolique, (je ne regarde que le premier):
dans $x_1x_2e_1\otimes e_1 + x_1y_2e_1\otimes e_2 + y_1x_2e_2\otimes e_1 + y_1y_2 e_2\otimes e_2$
on "aurait donc" viré $e_1\otimes e_2$ et $e_2\otimes e_1$, mais on envoie apparemment $e_2\otimes e_2$ sur $(-1)$ et .$(e_1\otimes e_1)$ sur $1$
Et celui de droite, c'est pire... Je n'ai pas d'image à proposer pour décrire une pseudo-motivationAide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Christophe a écrit:Tes deux premières photos, celles du haut Calli, elles sont là pour montrer AVANT RECOLLEMENT ce que seront les deux du bas, c'est ça?
Oui, c'est ça. On prend le disque posé à plat, on le découpe au niveau d'un rayon, on lui fait faire un tour de plus autour de l'axe vertical et on recolle ensemble les deux côtés du rayon coupé. Alors les points du bord du disque qu'on veut identifier se retrouvent les uns au dessus des autres et il suffit de déformer la surface pour les coller deux à deux. Sur l'illustration, les surfaces s'auto-intersectent parce que $\Bbb RP^2$ ne peut pas être plongé dans $\Bbb R^3$, mais il faut imager qu'elles passent au travers d'elles-mêmes. -
Calli, le procédé que tu décris me rappelle la surface feuilletée de Riemann servant de domaine de définition à la racine carrée pour en faire une fonction uniforme telle que décrite dans "l'Atlas des mathématiques". S'agit-il bien de la même chose ?
-
@Claude: ma référence c'est juste "le livre d'or du gars qui commet des bourdes"B-)
Merci d'avoir rectifié. Ceci dit je ne connais pas de "bonne définition" de l'algèbre extérieure.
Les jolis figures de Calli sont des projections dans R^3, elles possèdent un singularité parapluie de Whitney.
M. -
Sylvain : Je ne suis pas sûr d'avoir compris ton truc, qui doit être ça https://fr.wikipedia.org/wiki/Fonction_multivaluée#Surfaces_de_Riemann mais Wikipédia détaille peu :-S. Je pense que ce n'est pas la même chose car ton truc ressemble plutôt à un revêtement. Donc, si on doit faire des recollements, chaque point sera collé avec un autre point (l'autre point de la fibre), alors qu'on ne recolle des points que sur le bord dans mon exemple.
-
@max: tu dois savoir ça? C'est affaire de topologie ou faut aller plus loin et regarder le côté "difféo"?
Dans le plan projectif, on peut faire sortir le prisonnier en apparence à l'intérieur d'une petit ellipse en la déformant continument. Il n'y a pas d'intérieur et d'extérieur.
Est-ce que c'est général comme lien (notion d'intérieur-extérieur -- notion d'orientabilité)?
J'imagine que vus tes projets, ce sont des choses qui doivent t'être devenues très "copines" avec toi?Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Christophe l'architecte a écrit:Dans le plan projectif, on peut faire sortir le prisonnier en apparence à l'intérieur d'une petit ellipse en la déformant continument. Il n'y a pas d'intérieur et d'extérieur.
Ça c'est si tu dessines mal les plans de ta prison. Il existe quand même des prisons 100% sures dans le plan projectif réel. -
Christophe : savoir quoi ? J'avoue que j'ai pas suivi d'à quelle question tu te référais :-D
Par "intérieur", tu parles de quelque chose du type "théorème de Jordan" ? (Calli : si oui, pas sûr que tu aies raison sur tes prisons dans le plan projectif... tu penses juste à $\pi_1$ ou tu as quelque chose de plus dans ta manche ?) -
Ce que je voulais dire c'est que, si on décrit $\Bbb RP^2$ comme un quotient du disque, alors un petit cercle dans ce disque sépare le plan projectif en deux composantes connexes.
-
Calli : ah oui bien sûr, je ne sais pas pourquoi j'ai dit ça.
En fait plus généralement, dès que tu as une surface connexe , tu vas pouvoir faire la même chose, indépendamment de l'orientabilité.
Christophe : Bon naturellement si tu t'autorises à déformer ton lacet, la prison que Calli décrit peut effectivement se déformer en un point, mais si tu t'autorises à déformer les prisons, bah $\mathbb R^2$ n'a pas non plus de prison.
Par contre $\mathbb R^2\setminus\{*\}$ aurait effectivement une prison, mais lui est orientable.
Donc pas grand chose à voir avec l'orientabilité. -
@Calli : oui c'est un revêtement, de mémoire, et d'ailleurs pour l'anecdote j'avais lu sur Mathoverflow que Galois avait anticipé la notion de surface de Riemann dans le cadre de ce qu'il appelait sa "théorie de l'ambiguïté", ce qui laisse présager qu'il avait déjà en germe des conceptions similaires à celles de Grothendieck sur le sujet...et cela en mourant à 20 ans !
-
Christophe a écrit:Or sur le ruban de Möbius, sur la bouteille de Klein, c'est pas évident de calculer un volume orienté avec le quel tout le monde sera d'accord, non ?
Ben oui, vu que si tu regardes un petit carré sur le ruban de Möbius, par exemple, et que tu le remets à sa place en lui faisant faire un tour, comme il est à l'envers, son aire doit être égale à l'opposé de son aire.
Et sinon, l'algèbre extérieure de Claude, c'est l'espace vectoriel engendré par tous les produits tensoriels et où tu quotientes par le sous-espace engendré par les tenseurs purs avec une répétition ; c'est donc exactement ce que tu fais. Et les formes différentielles, c'est choisir des volumes orientés sur tous les plans tangents de manière régulière (et quand pas orientable équivaut, par définition, à ne pas pouvoir le faire de manière continue). -
Mauricio
Algèbre extérieure. Ne jamais démarrer à partir d'une usine à gaz. Ce que j'attache suffit pour commencer et ne pas se bloquer.
Mais ensuite ? C'est bien là le problème car ce n'est pas avec des définitions que l'on fait de maths. Il faut affronter de vrais terrains dans lesquels on peut faire débarquer l'algèbre extérieure (parfois, elle débarque toute seule ...etc...). Il y en a des dizaines et des dizaines : relations de Plücker, Determinantal varieties et Young Diagramms, Algebras with Straightening Law (Posets on Minors) ...etc...
Et à ce moment là, on est bien content d'avoir des références. Par exemple le Bourbaki A.III même si je pense qu'il est complètement raté. Mais avant de dire cela, il faut lire. Le A.III fait un peu près 180 pages. J'ai commencé il y a une vingtaine d'années, j'en ai bavé et j'ai pesté. C'est presque indispensable d'aller voir les archives de Bourbaki et les différentes évolutions de ce chapitre (en particulier les propositions de Chevalley).
Bref, il faut lire, lire, lire. Et après causer.
Pendant que j'y pense : 3 auteurs (dont Rota) On the Exterior Calculus of Invariant Theory http://kalx.net/dsS2011/BarBriRot1985.pdf. Introduction à lire : pas tendre avec le A.III de Bourbaki. Je ne suis pas tout à fait d'accord mais un peu quand même. -
Merci à tous, c'est très clair. Et pardon pour mon flou.
Pour la prison: ce que je veux dire (qui n'est pas possible dans IR², Max, mais l'est dans le Plan Projectif) c'est que si tu as un petit cercle C et un point à l'intérieur p, il existe une homotopie qui va continument déformer C jusqu'à en faire un point SANS JAMAIS TOUCHER p. (C'est aussi possible sur une sphère de dim2)
@Georges: du coup, je n'ai pas une connaissance satisfaisante de la différence entre le volume "de tout le monde" (Lebesguien), qui existe dans ces variétés, mais donne un nombre toujours positif, et les "formes volume". C'est intéressant, car ça sépare la notion de forme volume de volumen tout court. Est-ce que c'est juste une histoire de "possibilité de mettre un signe (négatif/positif)", ou est-ce que ça va "plus loin"?
@Max, tu parlais de $F_2$, mais n'est-il pas vrai qu'on "n'a qu'à" prolonger à $\C$ (je crois qu'on dit complexifier), puisque tout y est aussi orientable?Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Christophe a écrit:Pour la prison: ce que je veux dire (qui n'est pas possible dans IR², Max, mais l'est dans le Plan Projectif) c'est que si tu as un petit cercle C et un point à l'intérieur p, il existe une homotopie qui va continument déformer C jusqu'à en faire un point SANS JAMAIS TOUCHER p.
J'ai des doutes car $\Bbb RP^2 $ privé d'un point n'est pas simplement connexe. -
Je pourrais te faire une animation sur geogebra:
1/ Tu prends l'outil qui te trace automatiquement un cercle passant par 3 points imposés.
2/ Tu mets $p$ à l'intérieur de ton petit triangle $ABC$. Disons que $p$ est au dessus de $[BC]$
3/ Tu déplaces par exemple $A$, le fais passer par la droite $(BC)$ (ton cercle a alors l'apparence d'une droite), pus continues, ça redevient un cercle mais où $p$ est à l'extérieur. Puis tu le réduis à un point.
Ah ouiiiiiiiiiiiiiiiiiii, mais je réalise que la droite par laquelle on passe CHANGE LA NATURE de l'objet, pour moi, cette droite n'était qu'une instance du crecle parmi d'autre "grace au projectif", mais je suis allé un peu vite en besogne!!!! Tu as raison
olala, snif, j'aime bien le projectif, mais je lui ai accordé trop de pouvoirs magiques sur ce coup :-D (En même temps, dans le plan projectif, la différence "topologique" ou même difféomorphe" entre une droite et un cercle, je ne la vois pas trop, mais bon).Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Ok Christophe ce que tu demandes est plus clair comme ça: quand est-ce que$X\setminus\{p\}$ est simplement connexe ? (Pour $X$ une variété, cela ne dépend pas de $p$)
Comme le remarque Calli, $\mathbb RP^2$ privé d'un point n'est pas simplement connexe, c'est en fait le cercle à homotopie près si je ne m'abuse, et donc il a des prisons.
A contrario, $\mathbb R^3$ n'a pasde prison.
Une variété non orientable a nécessairement des prisons. En effet, soit $X$ une telle variété (qu'on peut supposer connexe et de dimension $\geq 2$). Je prends un point $p$ et une petit boule ouverte $B$ contenant $p$, puis j'applique Van Kampen à $X\setminus \{p\}$ et $B$.
En particulier, $\pi_1(X)$ est un quotient de $\pi_1(X\setminus\{p\})$.
Le premier est non nul (une variété simplement connexe est orientable), donc le second non plus. En particulier il y a une prison autour de $p$.
(À noter qu'à la fois Calli et moi avons utilisé $\pi_1$ pour quantifier les prisons : a priori Christophe autorise des déformations plus générales puisqu'il ne fixe pas le point base mais à conjugaison près cela ne change rien, donc cela ne change pas la non nullité)
Conclusion : non orientable $\implies$ prison (par exemple le plan projectif réel a des prisons); mais à part ça toutes les configurations sont possibls (orientable avec prison, orientable sans prison)
Ensuite par rapport à $\mathbb F_2$ vs $\mathbb C$, on ne parle pas de la même chose. Effectivement, une variété complexe est $\mathbb R$ (ou $\mathbb Z$)-orientable, donc si tu pars d'une variété et la complexifie elle deviendra orientable.
Moi je parlais de ne pas changer la variété du tout (garder le bon vieuc plan projectif réel), et de remarquer que dans ta conclusion que le volume est orienté ("$a\otimes b = - b\otimes a$") tu n'as tout simplement plus ce problème si $1= -1$.
Plus précisément, toute variété est (sans la modifier) $\mathbb F_2$-orientable.
Comme je le disais, on a une notion d'orientabilité, mais je ne sais pas s'il lui correapond une notion de volume -
Aaaahhhhhhhh, pardon Max, je vais lire ton post, mais je viens de réaliser que je comprends ton kiff, un cercle est homotope à une DOUBLE DROITE (à deux droites qui se croisent en gros, hum hum), et non une seule. Ah mais non, c'est bizarre aussi ça... Bon je te lis. En tout cas, c'est trop rigolo comme spécialité!!!!Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Je crois que je comprends!!
Mais j'ai un souci avec ... ah bah non, on ne demande pas que le lacet soit injectif. Donc, non, je n'ai pas de problème, c'est comme en TQ, "faut faire deux tours", autrement dit il me semble bien que le cercle est homotope à la réunion de deux droites distinctes. Dans mon "petit tour", elles se confondent au moment où le cercle devient droite.
Du coup existe-t-il une notion qui concrétise formellement ce que j'ai dit sur la façon de "faire sortir" un point de sa prison. En effet, je pense que tout le monde est d'accord que "je n'ai pas triché", donc que ce que je raconte n'est pas une homotopie, mais quelque chose de proche, où le PP n'est "devient simplement connexe" avec cette définition plus large?
Et je n'ai pas compris ce que tu appelles $F_2$-orientable. Pour moi, "orienter" c'est le fait d'associer CONTINUMENT une base infiniment petite à chaque point, e tj'ai quelques difficultés à voir de la continuité dans $F_2$.
GRAND MERCI EN TOUT CAS!Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Pour moi, une prison c'était un lacet injectif (les murs de la prison) qui sépare l'espace ambiant en deux composantes connexes (l'intérieur de la prison et son extérieur). D'où l'intérêt de préciser les définitions quand la terminologie n'est pas standard...Maxtimax a écrit:une variété simplement connexe est orientable
C'est difficile à prouver ça ?Christophe a écrit:quelque chose de proche, où le PP n'est "devient simplement connexe" avec cette définition plus large?
:-S -
Je n'y connais rien en géométrie classique, donc il va falloir plus détailler ce que tu as dit sur le plan projectif si tu veux que j'aie un espoir de comprendre :-D et d'éventuellement te répondre.
$\mathbb F_2$-orientable c'est pareil, mais c'est une $\mathbb F_2$-base :-D
En fait si tu veux une variété, localement ça ressemble à une boule euclidienne $B$, et donc localement "en fixant" $x$, c'est le même genre d'information que $B\setminus\{x\}$, soit une sphère $S$ (de dimension $1$ de moins).
Ce qu'on fait alors c'est qu'on prend "l'information homologique" locale en ce point (càd $H_{n-1}(S)$, enfin plus précisément, et c'est important $H_n(X,X\setminus\{x\})$). Chacun de ces groupes est isomorphe à $\mathbb Z$, mais pas canoniquement.
Le fait que ce soit pas canonique implique qu'on peut pas forcément tout recoller. En particulier si je choisis un isomorphisme avec $\mathbb Z$ (donc un $1$) et que je fais un petit tour le long d'un lacet bizarre, il n'est pas du tout à exclure qu'en revenant je tombe sur $-1$; c'est le problème de l'orientabilité.
Donc en fait on définit justement l'orientabilité comme le choix cohérent d'un isomorphisme avec $\mathbb Z$ (d'un $1$).
Si on aime la géo diff, on peut remplacer $\mathbb Z$ par $\mathbb R$, et on a de la chance, c'est équivalent à la définition d'orientabilité par forme volume (donc ce que tu dis : choisir continument une base de l'espace tangent) - mais en fait aussi ça ne change rien par rapport à $\mathbb Z$
En fait, plus concrètement, pour une variété différentielle, le fibré que j'ai décrit (le "machin" qui a en chaque point $x$, $H_n(X,X\setminus\{x\}; \mathbb R)$) ressemble à $\bigwedge^n TX$ (qui a en chaque point $x$ : $\bigwedge^n T_xX$, "le déterminant"), donc une base pour l'un (ce que j'appellerait $\mathbb R$-orientation) c'est une base pour l'autre (un "choix" de déterminant, donc de base)
Donc ce qu'il est amusant de repérer c'est que la topologie des fibres ne joue pas, c'est vraiment la topologie "horizontale" qui a un rôle. Bref, tout ça pour dire que si ce n'est que la topologie horizontale qui a un rôle, on peut remplacer $\mathbb Z$ par n'importe qui plutôt que $\mathbb R$. En particulier on peut mettre $\mathbb F_2$.
Et c'est là qu'on a de la chance : $\mathbb F_2$ est isomorphe à lui-même de manière unique : $Aut(\mathbb F_2) = *$. Donc les $H_n(X,X\setminus\{x\}; \mathbb F_2)$ sont tous canoniquement isomorphes à $\mathbb F_2$, et donc le problème de l'orientabilité disparait : tout est $\mathbb F_2$-orientable. -
Calli : ça dépend de ta définition d'orientabilité :-D
Avec la définition pour toute variété topologique, c'est relativement évident, puisqu'on a un "revêtement d'orientation", dont les sections sont précisément les orientations; donc si tu es simplement connexe, un revêtement admet forcément une section.
Avec la définition de géo diff, il faut (enfin j'ai l'impression) connaître la suite exacte longue d'homotopie d'une fibration : tu as un fibré vectoriel (en particulier une fibration) $\bigwedge^n TX\setminus \{0\} \to X$, de fibre $\mathbb R\setminus\{0\}$, et donc tu as $0\to \pi_1(\bigwedge^n TX\setminus \{0\})\to \pi_1(X)\to \pi_0(\mathbb R^*)\to \pi_0(\bigwedge^n TX\setminus \{0\}) \to *$
Maintenant si $X$ est simplement connexe, tout ça s'écroule, et en particulier $\bigwedge^n TX\setminus \{0\}$ a exactement deux composantes connexes. Selon les théorèmes que tu connais, on peut dire que ça suffit ou pas; mais en gros à partir de là c'est pas compliqué de voir que tu as une section de ta fibration, i.e. une orientation.
(il s'avère que les deux définitions d'orientation sont équivalentes lorsque ta variété est différentielle, mais évidemment toute variété n'est pas (ni même uniquement pour celles qui le sont) différentielle) -
@Max: je sais ce que c'est que les groupe d'homotopie (y compris $H_n(X)$, on avait eu une longue discussion où tu m'avais aidé), mais alors quand il y a deux arguments $H_n(X,Y)$ aucune idée de ce dont tu parles et en plus je parle bien d'homotopie, pas d'homologie à laquelle je ne connais STRICTEMENT RIEN.
Autant dire que je n'ai pas compris ce que tu m'as expliqué, en particulier, la substantifique moelle qui est que ce n'est pas topologique, mais "groupe" et que donc les choses ont un sens pour $F_2$ à l'ohrizontale.
Si tu pouvais simplifier ou vulgariser?
En fait, je veux juste comprendre le "substantifique", à savoir comment on voit que "ce n'est pas topologique". Car pour moi, orientatiblité = histoires de connexes, donc tu vois, je ne suis pas à la page.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Max a écrit:en géométrie classique, donc il va falloir plus détailler ce que tu as dit sur le plan projectif si tu veux que j'aie un espoir de comprendre grinning smiley et d'éventuellement te répondre.
Je vais te mettre une animation geogebra en lien dans la journée.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Attention, les groupes d'homotopie c'est $\pi_n$ ;-) $H_n$ c'est justement l'homologie ($H$ comme homologie si ça peut t'aider).
Sur les deux arguments : En gros en topo alg, quand on définit un invariant, on aime bien le définir aussi en une version relative : si on a $F(X)$ on essaiera de donner un sens à $F(X,A)$ pour $A\subset X$. Moralement c'est "la même information que $F(X)$ mais 'relativement' au sous-espace $A$".
Par exemple $\pi_n(X,A)$ ce sera des trucs où l'homotopie n'est pas autorisée à bouger sur $A$.
Pour l'orientabilité : en fait c'est topologique, mais c'est pas la topologie de $\mathbb R$, c'est la topologie de la variété ! La raison est que $\mathbb R$, topologiquement, il est débile; et $\mathbb R\setminus \{0\}$ aussi (c'est deux points en gros !)
J'essaie de simplifier, et donc je vais le faire pour une variété différentielle, en utilisant les espaces tangents: tu as une variété $M$. Pour chaque point $x\in M$, tu as un espace tangent $T_xM$, et tu veux en trouver une base continûment. En fait, pas vraiment, tu veux en trouver une orientation continûment. Trouver une base c'est beaucoup trop fort, on parle alors de parallélisabilité (beaucoup de sphères ne le sont pas). Je pense que c'était déjà ça un de tes points de confusion, donc j'appuie : orienter ce n'est pas trouver une base continûment, c'est trouver une orientation continûment. Je pense que comprendre ça sera essentiel pour la suite.
Donc il nous faut comprendre ce qu'est une orientation d'un espace vectoriel. Une orientation, c'est dire quelles bases sont "dans le bon sens", et quelles bases sont dans le mauvais sens. On peut savoir à l'avance si deux bases sont "dans le même sens" (le déterminant de l'une dans l'autre est positif) ou dans le sens opposé (négatif), donc en fait on a deux classes a priori, mais aucune des deux n'est en général privilégiée.
Donc en fait pour un espace vectoriel $V$ (pour le moment aucune topologie), "l'ensemble des orientations" a deux éléments, mais ils n'ont pas de nom particulier. Orienter ton ev, c'est leur donner des noms distincts, ou encore "en choisir une des deux" (trouver une bijection avec $2=\{0,1\}$ etc., tu vois l'idée).
Bon sauf que deux bases qui sont orientées dans le même sens, à un scalaire près, elles vont te donner le même déterminant. Et donc le fait qu'il y ait deux orientations se traduit dans le fait que $\bigwedge^n V^*$ ($n= \dim(V)$ - si tu veux, tu peux le voir comme l'espace des formes $n$-linéaires alternées sur $V$) soit isomorphe à $\mathbb R$ - le choix d'un tel iso est le choix de qui est positif et qui est négatif, donc le choix d'une orientation. Donc finalement "une orientation", c'est un élément non nul de $\bigwedge^n V^*$, à scalaire près.
Jusque là, ok ?
Donc orienter une variété différentielle, c'est faire ça avec chaque espace tangent, et continûment. Mais on vient de dire qu'une orientation de $T_xM$ c'est exactement un élément non nul de $\bigwedge^n (T_xM)^*$ ($n= \dim(M)$), et si on veut que ce soit un élément "qui varie continûment", on veut que ce soit une section (inverse à droite : le $s$ dans $p\circ s= id$) continue de l'application $\bigwedge^n T^*M\to M$ qui ne s'annule jamais; donc finalement une section continue de $\bigwedge^n T^*M\setminus \{0\}\to M$.
Bon, bah le truc c'est que les fibres (ce qui se trouvent au dessus de chaque point) de cette application, c'est $\bigwedge^n (T_xM)^*\setminus\{0\}$, donc $\mathbb R^*$ à iso près - donc un espace discret à deux points, à homotopie près (on se fiche des scalaires, donc on a le droit). C'est ce dernier point qui est le tueur. En fait, cette homotopie est canonique (de la même manière que tout groupe isomorphe à $\mathbb F_2$ l'est "canoniquement"), et donc notre application $\bigwedge^n T^*M\setminus \{0\}\to M$ elle ressemble énormément à une application $o(M)\to M$ ($o$ pour orientation) où chaque fibre a exactement deux points, discrets.
En fait on peut formaliser "ressemble énormément", mais le point clé c'est : une section de l'un donne une section de l'autre, et vice versa (c'est pas bijectif pour des raisons évidentes). Du coup, une orientation de $M$, c'est une section de $o(M)\to M$. Mais comme chaque fibre de cette application est un espace discret à deux points, tu vois bien que c'est uniquement la topologie de $M$ qui rentre en jeu, pas celle de $\mathbb R$.
En particulier, je peux remplacer mes deux points par les générateurs d'un groupe isomorphe à $\mathbb Z$ muni de la topologie discrète, et si je demande que ma section arrive dans les générateurs, ça ne change rien.
Plus généralement, on peut remplacer par n'importe quoi, vu que c'est la topologie de $M$ qui joue, pas celle de $\mathbb R$. Donc on peut mettre $\mathbb F_2$. Et là on arrive sur le même point que tout à l'heure : $\bigwedge^n \mathbb F_2^n \cong \mathbb F_2$, et il n'y a qu'un isomorphisme, donc qu'une orientation, parce que $1=-1$. -
Un grand merci!
Je comprends mal à partir de "varie continuement". Je pensais que tu allais écrire "de manière continue, donc on veut deux ouverts".
Je ne sais pas qui est l'application allant de $\wedge T_x(M)^n$ dans $M$.
Comme tu as précisé ce que veut dire "section" (j'oublie toujours ces mots n'accrochent pas pour moi, de même que le mot fibre, ni le mot "au dessus d'un point"), c'est bon, mais c'est l'occasion pour moi de retenir "enfin" ce que veulent dire ces mots (si c'est pas trop compliqué), car je fais une allergie depuis toujours (par exemple dès que j'entends des groupes de matheux les prononcer dans un bar, je vais fumer une clope).Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Une question simple: voulais-tu dire "on veut une fonction continue qui à chaque point de $M$ associe une forme linéaire alternée non nulle sur $(T(M))^n$?
Auquel cas, je comprends à la condition de mettre une topologie sur $(T(M))^n$ (Autrement dit $V^n$, autrement dit $V$?)? Or sur $Alternees(F_2^n)$, à part la discrète, je n'en vois pas, mais ce ne doit pas être ça.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Attention, elle ne va pas de $\bigwedge^n T^*_xM$ dans $M$, mais de $\bigwedge^n T^*M$ : avec l'indice $x$ c'est la fibre au-dessus de $x$ (= l'image réciproque de $\{x\}$). Cette application envoie tout $\bigwedge^n T^*_xM$ sur $x$, justement
Je veux dire "une fonction continue qui à chaque point $x$ de $M$ associe une forme linéaire alternée non nulle sur $(T_xM)^n$, pas $TM$ !
Et justement, ce qui importe finalement, c'est une topologie sur $\bigwedge^n T_x^*M \setminus\{0\} \cong \mathbb R^*$, sauf que ce dernier est équivalent (homotopique) à $2$ (topologie discrète) : donc ce qu'on en retient c'est que si on veut $\pm 1$ (au lieu de "un scalaire strictement positif ou strictement négatif", ce qui ne change rien du point de vue de la question de l'orientabilité), bah on se fiche finalement de la topologie de $\mathbb R$, puisque c'est juste la paire $\{\pm 1\}$ qui nous intéresse et rien d'autre (et elle est discrète dans $\mathbb R$)
Donc oui, c'est bien la discrète qu'on met sur $Alt^n(\mathbb F_2^n)$, ainsi que sur $\mathbb Z$ : ça ne change rien.
C'est ce que je voulais dire par "ce qui importe c'est la topologie horizontale"
PS : pour comprendre "horizontal", "au-dessus", "fibre", "section" etc. il faut comprendre le dessin mental qu'on se fait de la chose. On a notre variété $M$ qui est "en bas", avec plein de points dedans. Un point je peux le voir comme une inclusion $\{x\}\to M$. Chaque point a un espace tangent dans la variété, pictorialement :
$\xymatrix{T_xM \ar[d] \\
\{x\} \ar[r] & M}$
Le fibré tangent (c'est juste un nom, "fibré" vient de "fibre") c'est un truc global qui regroupe tous ces espaces tangents , pictorialement :
$\xymatrix{T_xM \ar[d]\ar[r] & TM \\
\{x\} \ar[r] & M}$
Un point du fibré tangent, c'est un point $x$ de $M$, et un vecteur $v\in T_xM$, donc en fait à chaque point du fibré tangent on peut associer un point de $M$ : ça nous donne une flèche $TM\to M$ :
$\xymatrix{T_xM \ar[d]\ar[r] & TM \ar[d]\\
\{x\} \ar[r] & M}$
Ici, tout est continu et ce diagramme est "cartésien", ça veut dire que $T_xM$ est précisément l'image réciproque de $\{x\}$ par la flèche $TM\to M$ : $TM$ c'est un bon gros truc avec tous les espaces tangents les uns à côté des autres. Vu l'image, on dit qu'il est au-dessus de $M$, et dès qu'on "tire" quelque chose de $M$ vers $TM$, on parle de "au-dessus": $ T_xM$ est au-dessus de $x$
Ensuite il s'avère qu'on peut faire pareil et recoller les $\bigwedge^n T_x^*M$ en un gros truc qui s'appelle $\bigwedge T^*M$, muni d'une flèche $\bigwedge^n T^*M\to M$ dont la fibre au-dessus de $x$ (l'image réciproque) est simplement $\bigwedge^n T_x^*M$
Une section d'une application $p$, c'est une $s$ telle que $p\circ s = id$. Dans notre dessin, avec disons $TM\to M$, ça donne un truc que je n'arrive pas à dessiner, mais qui explique très bien le mot section :-D
Du coup une section de $TM\to M$ c'est une application continue qui à chaque point associe un vecteur tangent, i.e. un champ de vecteurs. Une section de $\bigwedge^n T^*M\to M$, c'est une application continue qui à chaque point associe une forme $n$-linéaire alternée sur son espace tangent, et si on met $\setminus\{0\}$ c'est une forme $n$-linéaire alternée non nulle.
Maintenant, à homotopie près, $\bigwedge^n T^*M\setminus\{0\}\to M$ c'est un truc dont chaque fibre a deux points, discrets ($\mathbb R_{>0}$ et $\mathbb R_{<0}$, qui sont contractiles, donc des points au niveau de l'homotopie) : donc la topologie "verticale" (celle de chaque fibre) n'a que peu d'intérêt, et c'est la topologie horizontale (celle de $M$) qui en a.
Tu peux penser à un fibré comme une sorte de produit $M\times $ la fibre, mais qui est twisté - c'est de là que vient mon idée de "horizontale" vs "verticale" , chaque fibre est vue verticalement si tu veux.
On peut faire une analogie plus précise : les fibrés $E\to M$ sont aux produits d'espaces ce que les extensions non triviales de groupes (i.e. les suites exactes $1\to H\to G\to Q\to 1$) sont aux produits de groupes (naïvement, $G$ est un "produit twisté" de $Q$ et $H$) -
Au fait merci Christophe et Calli, du coup je me suis enfin motivé à poser l'équivalence entre les deux notions d'orientabilité (je savais qu'elles étaient équivalentes mais j'avais jamais ni vu ni écrit de preuve, du coup je me suis enfin motivé à l'écrire et c'était pas mal :-D )
-
Merci c'est vraiment très précis. Il y a une chose qui m'échappe, c'est pourquoi ne pas tout simplement prendre le même espace tangent en chaque point, ce n'est pas clair pour moi, mais, je ne me rappelle de la notion de variété qu'avec des histoires de cartes, aussi pour moi, l'espace tangent c'est $\R^n$, ou éventuellement pour dire qu'on en met un pour chaque $x$ de $M$, c'est "une copie" de $\R^n$.
Au final, donc, une orientation c'est une application continue, donc qui à chaque $x\in M$ associe une forme alternée de son espace tangent. Mais puisque F_2 (enfin disons plutôt $F_3$ tiens!) est discret, on va juste demander une application localement constante? Non? Autrement, quand je parlais de connexe... Il doit y avoir quelque chose que j'ai loupé.
En effet, a priori, même si "on s'en fiche" que ce soit à un scalaire près, l'espace tangent est imposé comme une donnée de la variété? Donc comment peut-on "le changer" en $F_2$ (ou $F_2(x))$ si besoin?
Très grand merci à toi. C'est à nous de te remercier, j'étais au soleil caniculaire, moi pendant ce temps (bon à Paris bof bof, mais j'avais trouvé de la verdure assez étonnamment étendue))Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Christophe a écrit:pourquoi ne pas tout simplement prendre le même espace tangent en chaque point, ce n'est pas clair pour moi, mais, je ne me rappelle de la notion de variété qu'avec des histoires de cartes, aussi pour moi, l'espace tangent c'est $\R^n$, ou éventuellement pour dire qu'on en met un pour chaque $x$ de $M$, c'est "une copie" de $\R^n$.
Les espaces tangents $T_x M$ ne sont pas canoniquement isomorphe à $\Bbb R^n$. Donc on se contente d'avoir des espaces tangents intrinsèques et de dimension $n$ mais sans base canonique, c'est plus simple comme ça. Les identifier explicitement à $\Bbb R^n$ serait artificiel en général. -
Dans l'ordre :
Pour l'espace tangent, justement : en chaque $x$, c'est une copie de $\R^n$, mais ce dernier a beaucoup d'automorphismes, et en particulier l'identification $T_xM\cong \R^n$ n'est pas canonique.
Pour te donner une idée, prenons un cas très simple : je prends une fonction très gentille $f :\R^m\to \R$ et $M := f^{-1}(\{0\})$. Dans les cas favorables (je ne détaillerai pas, c'est pas compliqué mais ça ne t'intéressera pas pour le moment), $M$ est naturellement une variété différentiable, et en $x$ l'espace tangent à $M$ s'identifie à $\ker (d_xf)$ ($d_xf$ est, elle, définie sur $\R^m$, qui est l'espace tangent à $x$ dans $\R^m$).
Ou encore, un point de vue plus simple à visualiser : l'espace tangent en $x$ est le sev de $\R^m$ consistant en les $v\in\R^m$ qui sont $\gamma'(0)$, pour au moins un $\gamma : ]-\epsilon, \epsilon[ \to M$ différentiable. Si tu imagines $S^2\subset \R^3$ par exemple, l'espace tangent en $x$ est celui qu'on imagine (à une translation par $x$ près : l'image mentale en fait un sous-espace affine de $\R^3$ puisqu'on rajoute $x$) : tu vois qu'il bouge avec le point, et en fait on ne peut pas faire autrement, c'est un théorème ($S^2$ n'est pas parallélisable)
(Calli : c'est pas juste que ce serait artificiel, c'est que ce n'est pas possible)
(juste pour répondre : tu fais bien de prendre $\mathbb F_3$ puisque pour $\mathbb F_2$ l'ensemble d'arrivée est un singleton :-D )
Non, elle ne sera pas localement constante, parce que justement, ce n'est pas à valeurs dans $\bigwedge^n \mathbb (F_3^n)^*$ qu'on arrive, mais dans $\bigwedge^n (V_x)^*$, avec $V_x\cong \mathbb F_3^n$ pour tout $x$. Mais cet isomorphisme n'est pas unique, canonique ou quoi que ce soit. En gros $V_x$ bouge avec $x$ et tu n'as pas une identification fixée avec $\mathbb F_3$.
Une orientation te donne justement une telle identification, et donc effectivement, si une orientation existe, le truc vers lequel tu vas est non connexe, et donc tu as des applications "localement constantes".
En fait, je pense que la confusion vient du point suivant :
Prenons un espace $X$ (on peut penser à une variété mais c'est pas nécessaire), et une application continue $p: Y\to X$. Je prends un point $x\in X$ et je pose $F := p^{-1}(\{x\})$; et je suppose que pour tout $s\in X$, il existe un homéomorphisme $p^{-1}(\{s\}) \cong F$. Attention, je ne fixe pas cet homéo dans mes données, et je ne demande pas qu'ils soient compatibles : je demande qu'il existe un homéo, "abstraitement".
Alors on peut penser à $Y$ comme "un produit twisté" de $X$ par $F$, et à $p$ comme "la projection sur $X$" de ce produit twisté. Du coup, les sections $X\to Y$ (quelqu'une tel que $p\circ$ elle $=id_X$) se pensent comme des "fonctions continues $X\to F$ généralisées". En effet, si $Y=X\times F$ et $p$ est la projection (le cas où le produit n'est pas twisté, le cas simple), alors une section c'est exactement la même chose qu'une application continue $X\to F$.
Ici, c'est pareil : tu as un "fibré" $p : TM\to M$ dont les fibres sont toutes homéomorphes à $\R^n$, mais $TM$ n'est pas $M\times \R^n$ (en général, même à homéomorphisme près). Pareil dans le cas où les fibres sont $\mathbb F_3$ : ton truc n'est pas $M\times \mathbb F_3$ (qui serait trois copies de $M$, topologiquement), même à homéomorphisme près.
Je prends un exemple : tu as une projection canonique $S^2\to \mathbb RP^2$, en chaque point, la fibre est un espace discret à deux points (en fait tu as beaucoup mieux, il y a même une condition de cohérence locale, mais je ne voulais pas rentrer dans les détails). Pourtant $S^2$ n'est pas du tout du tout (mais alors pas du tout) $\mathbb RP^2\times 2$. ça c'est ok ?
Et bah pour $\mathbb RP^2$, le $o(M)$ (donc $o(\mathbb RP^2)$) c'est exactement $S^2$ à homéomorphisme près. En particulier il n'y a pas de section : $\mathbb RP^2$ n'est pas orientable. Pourtant, une telle section reviendrait à assigner "en chaque point, un élément de $2$".
Le problème c'est que l'identification de la fibre avec $2$ n'est pas cohérente sur tout $\mathbb RP^2$ : si tu identifies la fibre à $2$ en un point, et suis un petit lacet en identifiant de manière cohérente localement à chaque fois la fibre à $S^2$, et que tu suis un lacet "méchant", à la fin ton identification sera renversée !!
Donc il y a de la disconnexité dans chaque fibre, mais le fibré, lui, n'est pas disconnexe. Enfin, si, parfois : quand $M$ est orientable :-D (c'est un théorème)
Quant à la question "comment prendre $\mathbb F_2$ alors que l'espace tangent est donné (et c'est $\mathbb R$) ?" - c'est que la notion de $\mathbb F_2$-orientabilité n'utilise pas l'espace tangent. C'est ce que j'ai essayé d'expliquer plus tôt : quand tu remplaces $\bigwedge^nT^*_xM$ par $H_n(M,M\setminus\{x\};\mathbb R)$, tu obtiens la même réponse à la question "le fibré a-t-il une section ?". Mais tu vois que le deuxième dépend de $\mathbb R$; donc tu peux ensuite remplacer ce $\mathbb R$ par $\mathbb Z$, puis en fait par $\mathbb F_2$ (ou n'importe quel $R$).
Bref, passer à $\mathbb F_2$ requiert de changer un peu la définition d'orientabilité, mais c'est équivalent, donc tout va bien. Et en fait, on pourrait penser que c'est débile, mais il y a des théorèmes de la forme "si machin est orientable alors blah" qui se généralisent facilement en "si machin est $R$-orientable, alors $R$-blah", et $R$-blah peut être très intéressante, même pour des $R$ comme $\mathbb F_2$.
Je pense en particulier à la dualité de Poincaré, qui est valable pour toute variété, si tant est qu'on se met en caractéristique $2$ -
Ah d'accord, mais je n'ai pas pensé que $\R^n$ est fourni avec sa base, pardon, donc en fait oui, c'est le même espace vectoriel de dimension $n$. Et finalement, ce qu'on demande à une orientation, c'est une application continue de $M$ dans cet espace?
Mais je n'arrive toujours pas à voir comment "greffer" $F_3$ (je prends $F_3$ exprès plutôt que $F_2$, pour maintenir la (éventuelle) non orientabilité).
.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Je n'ai pas encore lu MAx, nos posts se sont croisés, je vais aller lire, car la réponse est peut-être dedans!Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
http://www.les-mathematiques.net/phorum/read.php?3,2010912,2011558#msg-2011558
Merci Max. La définition de l'orientabilité que je connais est pour les variétés différentielles. J'ai regardé la définition de Wikipédia pour les variétés topologiques (voire les espaces topologiques ::o) mais j'ai du mal à me faire une idée de ce qu'est $H_n(X,X\setminus\{x\})$, et plus généralement de $H_n(X,A)$ pour $A\subset X$.
Je transforme ce que tu m'a dit en une preuve qui utilise les notions que je connais :
Soit $M$ une variété différentielle $\mathcal{C}^1$ de dimension $n$, simplement connexe. Soit $g$ une métrique riemannienne sur $M$. Elle induit une métrique $g'$ sur $\Lambda ^n T^*\!M$. Soit $S\Lambda ^n T^*\!M = \{(x,X)\in \Lambda ^n T^*\!M \mid g'(X,X)=1\}$. Alors $S\Lambda ^n T^*\!M\to M$ est un revêtement à deux feuillets de $M$. Or $M$ est simplement connexe et localement simplement connexe donc il est son propre revêtement universel. Donc $S\Lambda ^n T^*\!M$ possède deux composantes connexes et le choix de l'une d'entre elles donne une orientation. -
Ok, j'ai compris (en fait la réponse de Calli m'avait débloqué sur le reste) et GRAND MERCI. Mais pour la chose chose que je n'ai pas comprise, (prendre $F_3$ à la place de $\R$), tu es en train de me dire qu'il faut que je comprenne ce que veut dire $H(X,Y; K)$? Que "toute la question serait là dedans?Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Calli : oui effectivement, pas besoin de la suite exacte - c'est mieux avec des revêtements; je m'en suis rendu compte après en me disant que tu serais capable de trouver ;-)
Si tu veux on pourra reparler de $H_n(X,A)$ et $H_n(M,M\setminus \{x\})$ (pour ce dernier, même si on peut le définir pour un espace topologique quelconque, il vaut mieux avoir une variété en tête, enfin je trouve) -
Christophe: bah si tu veux être précis, oui, c'est comme ça qu'on définit la $K$-orientabilité. Mais je pense que tu peux comprendre "avec les mains" sans ça; juste ce ne sera pas précis.
-
Justement j'ai un gros atout, la précision je la remets tout seul en général, j'ai souvent juste besoin d'avoir compris, je suis producteur de formel automatiquement comme d'autres comptent les moutons :-D
En fait, j'ai cliqué sur le lien de Calli. Donc, je rends les armes, vu qu'ils définissent l'orientatibilité d'un espace topologoque, je ne peux plus passer quelques jours de plus sans avoir compris.
Donc ......... [size=x-small]si tu voulais bien me résumer ce que veut dire $H_n(X,Y,K)$ .....[/size]Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Ou si ça revient au même ce que veut dire $\pi_n(X,Y,K)$ éventuellement puisque je sais ce que veut dire $\pi_n$.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi
-
Non, l'étude de $\pi_n$ est complètement différente de celle de $H_n$ malheureusement
(pour tout te dire, pour $n>0$, $H_k(S^n) = \mathbb Z$ pour $k=0,n$ et $0$ autre part, alors que pour $n\geq 2$, on ne connait pas tous les $\pi_k(S^n)$... et beaucoup pensent qu'on ne saura jamais - on en a déjà parlé)
J'essaierai de t'expliquer ça ce soir si j'ai le temps, sinon un autre jour, mais ça arrive, promis ;-) -
Merci, de mon côté, je vais un peu surfer.
Oui on en avait parlé, mais je ne me rappelle pas la sensationnelle phrase:Max a écrit:et beaucoup pensent qu'on ne saura jamais
très alléchante :-D
Si tu peux préciser. Et oui, pour le reste prends ton temps.Aide les autres comme toi-même car ils sont toi, ils sont vraiment toi -
Bah déjà il y a un aspect empirique naïf qui est qu'on ne repère aucune régularité et que la complexité de ce qu'on calcule semble indiquer une complexité intrinsèque (on a des $\mathbb Z/24$ qui apparaissent par endroits) .
Mais on avait déjà discuté de la complexité théorique, je ne retrouve plus le fil en question (tu sauras peut-être mieux faire que moi), j'y avais posté des liens vers des documents qui indiquaient que des choses comme "calculer $\pi_n$ de tel complexe simplicial fini" étaient indécidables, ou du moins NP-complètes (je ne sais plus trop les résultats précis, j'avoue...), et que ça suggérait qu'il en était de même des sphères.
Il faudrait retrouver le fil en question et les documents que j'avais cité.
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 7 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 52 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres