Trapèze
Bonjour,
Je voudrais justifier, que le trapèze isocèle (strict) ci-dessous possède un axe de symétrie : la médiatrice des bases (qui sont confondues).
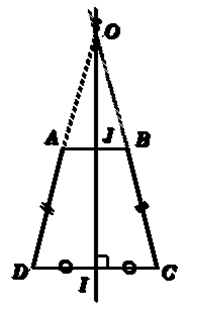
Ca semble facile mais je veux me limiter à utiliser que des outils de Sixième.
Les prérequis sont les suivants :
- Propriétés des droites parallèles, perpendiculaires ;
- Médiatrices, axe de symétrie d'un angle ;
- Symétrie axiale ;
- Axes de symétrie des triangles isocèles et conséquence (sans les réciproques) ;
- J'accepte les conditions CCC, CAC et ACA s'il le fallait vraiment.
J'ai effectué des constructions (voir le dessin plus haut).
Je voudrais justifier, que le trapèze isocèle (strict) ci-dessous possède un axe de symétrie : la médiatrice des bases (qui sont confondues).

Ca semble facile mais je veux me limiter à utiliser que des outils de Sixième.
Les prérequis sont les suivants :
- Propriétés des droites parallèles, perpendiculaires ;
- Médiatrices, axe de symétrie d'un angle ;
- Symétrie axiale ;
- Axes de symétrie des triangles isocèles et conséquence (sans les réciproques) ;
- J'accepte les conditions CCC, CAC et ACA s'il le fallait vraiment.
J'ai effectué des constructions (voir le dessin plus haut).
Réponses
-
Ok.
La figure propose les choses connues.
Attention d’ailleurs, on ne sait pas a priori que les trois droites sont concourantes en O.
Sauf à avoir une définition de trapèze isocèle particulière (un triangle isocèle qu’on coupe par une droite parallèle à sa base).
Ici je pars du principe que c’est « au moins deux côtés parallèles et les deux autres côtés de même longueur ».
Une piste est de démontrer que J est au milieu de [AB].
Enfin mieux : que A est symétrique de B par rapport à (IJ).
L’image de D est C, ça c’est par définition.
Sait-on que les angles du trapèze sont égaux, en D et C ? -
Salut Dom !
Pour les trois droites tu as raison mon dessin est trompeur.
Pour l'histoire des angles en D et en C c'est un résultat que je veux établir comme conséquence de celui-ci. -
Hello,
A mon humble avis, ces contraintes ne permettent pas d'apporter une preuve.
Dans la collection "série rouge" une preuve est donnée mais avec des outils de Cinquième. X:-(
Un stratégie consiste à montrer que les angles en D et C ont la même mesure d'abord, la suite un jeu d'enfant... -
Ok ! Bon bah effectivement cela semble sans espoir avec de telles contraintes.
Merci @FLEURISTIN -
Avec les définitions que j’ai choisies (enfin ce sont les définitions de tout le monde je crois...) ça ne marche pas. Le théorème est faux.
Par exemple (c’est le seul je pense) un parallélogramme non rectangle est un trapèze isocèle et n’a pas d’axe de symétrie.
Il faut donc ajouter quelque chose.
Au choix :
- les deux côtés parallèles de longueurs distinctes
- les deux autres côtés (ceux qui sont de même longueur) non parallèles
On s’embarque dans du moche... -
J'ai personnellement toujours été embêté par la définition du trapèze au collège , on voudrait que ce soit tout quadrilatère convexe avec deux côtés parallèles mais on a le problème du parallélogramme . On peut dire que c'est aussi un trapèze mais alors est-il isocèle ? On peut éviter les embrouilles en définissant un trapèze isocèle comme un trapèze avec un axe de symétrie mais ce n'est pas naturel au niveau 6ème . On pourrait aussi définir un trapèze comme un quadrilatère ayant seulement deux côtés parallèles mais alors on rentre dans des complications pénibles quand il faut expliquer qu'une figure est un trapèze : il faudrait monter que le quadrilatère n'a que deux côtés parallèles . J'ai fini par laisser tomber les détails car en 6ème on ne démontre pas vraiment . Un trapèze isocèle est un trapèze avec deux côtés égaux et il a un axe de symétrie ( on oublie volontairement le parallélogramme pour ne pas apporter de confusion ) .
Domi -
Oui.
J’aime bien l’idée qu’un trapèze soit un triangle coupé par un droite parallèle à un côté.
Ça évite le parallélogramme.
Mais en maths on n’aime pas trop exclure avec les définitions, d’habitude. -
@Domi, le parallélogramme a deux paires des côtés opposés parallèles, alors qu’un trapèze a une paire des côtés opposés parallèles et deux autres qui ne le sont pas. Aucune ambiguïté ;-)
-
vorobichek,
Ça encourage à dire que le rectangle n’a pas les quatre côtés de même longueur.
Il faut se méfier... -
@Dom, je viens de lire le wiki russe et anglais. Il semblerait qu’il y a deux définitions. Une qui exclut les parallélogrammes (ce que j’ai appris) et l’autre où les parallélogrammes sont des trapèzes particuliers. Je ne savais pas... A mon avis, la première facilite la vie au collège.
-
Je suis d’accord, ceci dit.
En fait je ne me souviens pas de ce que j’ai appris.
Mais dans mon esprit, longtemps c’était comme tu le dis.
Ensuite j’ai deux pistes :
- celle qui me semble la moins excluante donnée par wiki français.
- celle qui serait un triangle tronqué (qui revient à celle que tu considères comme plus pratique
Notamment pour le trapèze rectangle, on imagine bien un triangle rectangle tronqué.
Cependant : même avec ça, la question originale du fil me semble bien difficile à résoudre. -
Il y a eu une époque ( que je ne regrette pas vraiment ) où l'on donnait des définitions très précises au mépris de l'intuition des élèves : un parallélogramme est un quadrilatère dont les diagonales se coupent en leur milieu , un rectangle est un parallélogramme à diagonales égales ...
Tout ça nous donne un confort mathématique mais les élèves y perdent leurs bases . Il faut rester le plus proche possible des idées élémentaires que les élèves se font des choses ne serait-ce que pour pouvoir en démolir certaines : un carré n'est pas un losange car le losange n'a pas d'angle droit .
Mais je vais quitter la barque sans avoir vraiment aucune certitude sur la meilleure façon de présenter les choses .
Domi -
Si un parallélogramme n'est pas un trapèze, alors, pour être cohérent, un carré n'est pas un rectangle, un triangle équilatéral n'est pas isocèle ...
-
Avec les triangles égaux. JIC et JID. Deux parallèles, donc la perpendiculaire à (CD) est perpendiculaire à (AB). D’où l’égalité des triangles JCB et JDA. On en déduit que JA = JB.
Les cas d’égalité des triangles sont de base chez Euclide, pour démontrer les autres propositions. Si on supprime les démonstrations du collège, il est inutile de consacrer à ces triangles égaux le temps nécessaire en classe (beaucoup d’heures). Dans ce cas, il faut supprimer totalement la géométrie et ne plus parler de segment, de cercle et surtout pas de symétrie parce que ça n’a plus aucun sens. -
Les triangles égaux sont une forme de triche pour démontrer ce truc je trouve.
Ça contient tout, surtout les angles et c’est ce que l’on veut démontrer.
Mais en effet on ne semble pas avoir le choix.
Dans une moindre mesure j’aurais envie d’accepter les résultats sur les translations (ici c’est un triangle isocèle dont on a écarté un côté pour former le trapèze). Mais en 6e, non, pas de translation. -
On parle ici d'élèves de 6ème pour qui l'observation tient lieu de preuve : ici il n'y a rien à démonter car tout est visuellement évident . Au collège je réserve les quelques démonstrations que je propose aux élèves à des propriétés qui ne sont pas visuellement évidentes : somme des angles d'un polygone , Pythagore , cercle circonscrit ... D'ailleurs dans les programmes on propose de plus en plus de démonstrations dans le domaine numérique ce qui ne me semble pas forcément une bonne idée .
Domi -
Pourquoi de la triche ? Fais-tu référence au fait que certaines démonstrations d’Euclide, où l’on fait vaguement glisser une figure sur une autre, ne sont plus très bien acceptées aujourd’hui ? Dans ce cas, je suis d’accord. Sinon, ces cas d’égalité sont montrés, de mémoire, assez vite dans le livre en question et le reste repose dessus.
-
Oui Domi mais justement, les maths ne se démontrent pas à coups de « on voit que ».
L’école a fait ça et je ne la blâme pas puis au collège on bannit la démonstration par « ça se voit » en pratiquant avec des raisonnements.
Oui, Sato, quand je dis de la triche il faut nuancer.
Les axiomes des triangles égaux, j’aurais envie de n’en parler qu’en 5e après avoir fait des maths en 6e et il y a de la matière (les côtes opposés d’un rectangle sont parallèles, un quadrilatère avec trois angles droits est un rectangle, toutes les choses qui relèves de la symétrie axiale, etc.).
C’est ça, les glissements vagues, ça ne m’intéresse que pour « l’idée de la preuve » mais pas en tant que preuve.
En effet on a vite fait d’avoir un gamin qui saura user de ce genre d’arguments « oui mais là, non, on ne peut pas ». -
On est bien d'accord Dom mais il est évident qu'on ne démontre pas tout au collège et il faut choisir de démontrer en priorité ce qui ne saute pas aux yeux des élèves . Démontrer par exemple qu'un quadrilatère avec trois angles droits est un rectangle est une véritable perte de temps et instille dans la tête des élèves que démontrer c'est couper les cheveux en quatre pour pas grand chose . De même en 5ème démontrer que la somme de deux nombres pairs est pair me laisse un peu dubitatif . Je réserve donc les démonstrations aux propriétés qui n'ont rien d'évident pour montrer leur incroyable efficacité .
Domi -
Je suis d’accord pour faire des choix.
Par contre je trouve que « 3 angles droits => rectangle » est pertinent à démontrer. -
Pertinent sans doute mais tu ne va convaincre que des convaincus . Faire chercher pendant un bon moment un cercle passant par trois points non alignés puis démontrer en trois coups de cuillère à pot que la solution existe et est unique , là tu as tout le monde avec toi .
Mais chacun a un public et une sensibilité différente .
Domi -
Oui, oui, chacun sent ce qu’il peut et doit faire.
Le cercle circonscrit était au programme de 5e il y a bien longtemps. Les « droites remarquables » sont parties assez rapidement.
En fait, je remarque que c’est la classe de 6e qui a le moins changé en terme de programme avec les dernières réformes.
Édit : je réponds plus tard pour « isocèle » car la question est posée à Éric. -
@ Domi : je ne parle pas de trapèze isocèle ou pas en 6eme puisque je n'ai pas de 6emes (réponse facile j'en conviens).
Pour le coup, je suivrais ce qui est dit sur Wikipedia : deux angles adjacents à une même base sont égaux.
https://fr.wikipedia.org/wiki/Trapèze -
Le plus communément admis est « triangle qui possède au moins deux côtés de même longueur » et parfois on trouve « triangle qui possède deux côtés de même longueur » et ça donne une ambiguïté sur « exactement deux » ou « au moins deux » et je pense que c’est ce que voulait soulever Domi, non ?
Édit : ok, hors sujet après correction de Domi. -
Non , je parlais de trapèze, pas de triangle. J'avais tapé triangle par réflexe mais j'ai corrigé immédiatement.
Domi -
J’ai lu quelque part, probablement dans le bulletin vert, que la définition du trapèze isocèle avait fait couler beaucoup d’encre à l’époque.Algebraic symbols are used when you do not know what you are talking about.
-- Schnoebelen, Philippe -
Pour le parallélogramme en 5ème, je prends la liberté de me détacher de 95% de la littérature mathématiques de 5ème à propos de la définition en posant que c'est un quadrilatère non croisé qui admet un centre de symétrie. Toutes les propriétés en découlent.
Je ferais bien la même chose avec d'autres figures comme le triangle isocèle mais cette figure a été trop souvent abordée en primaire par une autre définition.
Avec le trapèze isocèle cela pourrait peut-être passer, même si je n'ai pas réfléchi à une définition faisant appel à un axe de symétrie et qui ne soit pas une usine à gaz pour des 6ème. -
Alors que moi je préconise « parallélogramme = quadrilatère avec côtés opposés parallèles ».
Je trouve que c’est contourner les difficultés.
Idem avec « quadrilatère avec diagonales de même milieu ».
C’est théoriquement très malin mais je n’aime pas du tout.
Bien entendu que c’est difficile ensuite.
Enfin, dès que la symétrie centrale transforme une droite en une droite parallèle (démontrable en 6e), on a le centre de symétrie assez vite.
Les plus difficiles sont les réciproques du genre « si côtés opposés égaux alors parallélogramme » et cela quelle que soit la définition. -
D'un point de vue théorique, on peut envisager que ce sont les symétries qui font les figures et non l'inverse. En tout cas j'ai pleinement conscience de ce que tu écris, Dom. C'est ce que j'ai trouvé de mieux pour démontrer tout de même quelques petites choses et avoir le temps de scratcher...
-
Si tu prends côtés deux à deux parallèles, tu fais comment pour le cas dégénéré où les sommets sont alignés ?
Tu peux toujours dire que ça n'existe pas, mais pour la translation, il va falloir en parler.
Si tu prends les diagonales qui se croisent en leur milieu, plus de problème avec le cas dégénéré. -
C'est un peu ce que je disais au début du fil , si on ne veut pas être embêté avec les démonstrations on choisit une définition savante mais contre-intuitive pour les élèves . On va produire une belle construction mais que va-t-il rester dans la tête des élèves ?
Domi -
Je suis d'accord avec toi, Domi.
Dis-moi Éric, on pourrait dire la même chose pour un simple rectangle : ABBA en est-il un ?
Faut-il alors définir un rectangle avec "quadrilatère avec les diagonales de même longueur et de même milieu" au lieu de "quadrilatère avec quatre angles droits" ?
[small]D'ailleurs, avec certains cas dégénérés, on perd parfois les côtés opposés parallèles, qui doit bien être une propriété, quelque part, non ?[/small]
De même, AAAA est-il un carré ?
"Oui" est une bonne réponse et "non" en est-une aussi, enfin, on s'est compris...
Je préfère utiliser l'étymologie/la sémantique des mots pour définir les objets, au collège.
Au lycée, expliquer qu'on change de définition pour englober les cas dégénérés me semble très pertinent d'autant plus qu'ils connaissent (...c'est vite dit, c'est la théorie...) les caractérisations. -
Dom si tu veux utiliser l'étymologie pour donner tes définitions, il faut presque tout baser sur les angles (cf par exemple l'étymologie de polygone) et AAA ne définit pas un angle. Ou j'ai mal compris.
Ma définition du parallélogramme n'est pas si contre intuitive pourvu qu'on s'y prenne bien, c'est permis car qui a déjà vu un parallélogramme ailleurs que dans son imagination à cet âge ?
Chapitre 1 : la symétrie axiale et les figures qu'elle engendre.
Et on peut tout de suite avoir
Chapitre 2 : les parallélogrammes.
Bonne journée et bon retour prochain aux élèves, juste à temps pour des parties de baccalauréat (le jeu évidemment) endiablées... Enfin pas chez moi ! -
« Parallélogramme » et « rectangle », oui ce sont des figures qui de mon point de vue portent très bien leurs noms.
Elles n’ont pas à être dégénérées, a priori.
Puis la théorie venant, on souhaite englober tous les cas ce qui suggère, pour des raisons de preuves plus courtes, qu’il en redonne des définitions plus « stables » et « généralisantes ».
En effet, je me fiche que l’on se dise au collège qu'on ne sait pas décider si AAAA est un rectangle ou pas.
PS :
Tu as raison, « polygone » signifie « plusieurs angles ». -
@Dom : l'intérêt des cas dégénérés est de pouvoir parler de vecteurs égaux dans tous les cas et de définir l'image d'un point par une translation dans tous les cas (si tu définis les translations à partir des parallélogrammes et les vecteurs à partir des translations). Tu as donc besoin de cas dégénérés de parallélogrammes, mais tu te moques d'appeler ce cas dégénéré un rectangle ou pas, ça n'a pas d'intérêt.
-
Et bien je suis complètement d’accord avec ça.
Comme au collège il n’y a pas « les vecteurs » et que les translations sont du « on voit bien que, en glissant », les intérêts du lycée n’existent pas (encore) au collège. -
Les translations sont du "on voit bien que" si tu choisis de faire du "on voit bien que". Rien n'interdit de ne pas faire du "on voit bien que".
On ne peut pas constamment se plaindre que l'on ne fait plus de math au collège et inviter à ne pas en faire à la moindre difficulté (à moins d'être un inspecteur intellectuellement malhonnête). -
À ma dernière inspection j'avais choisi de ne pas faire du "on voit bien que", bien mal m'en a pris, l'entretien a duré 1h30. Il faut dire aussi que je n'ai pas fait de concession. Mais le résultat est que cela figure dans mon rapport, que la séance était "trop compliquée"... Du coup ça n'incite pas non plus, Éric, à maintenir le niveau contre vents et marées.
Sinon je suis d'accord, il faut faire dégénérer systématiquement toutes les figures, peu importe le nom donné, sinon une droite est un cercle. -
Ok.
Je préconise de définir les translations sans « on voit bien que ».
Pour ça, ça ne me dérange pas de définir en distinguant les cas dégénérés et les cas plus consistants.
Si on veut être cohérent, j’attends toujours de voir la définition de ce qu’est un rectangle qui englobe les cas dégénérés.
J’affirme que personne ne le fait.
Je me trompe nécessairement, qui peut dire « j’en connais au moins un qui le fait » ?
Remarque : idem pour les homothéties d’ailleurs, sortir des programmes ne me dérange pas.
On définit facilement le cas « positif » puis le cas « négatif » avec des notions de 6e (et c’est en 3e qu’il le fait).
Je crois que c’est bien de le faire. -
@ Dom : j'ai dit au-dessus que ça ne présente pas d'intérêt pour le rectangle.
Dans le genre "on voit bien que", un où il est difficile de détecter l'escroquerie est la "transitivité du parallélogramme". Si $ABCD$ et $CEFD$ sont des parallélogrammes, alors $ABEF$ est un parallélogramme (et je ne parle même pas des cas dégénérés ...). -
Ok Éric,
Cette question de l’intérêt pour celui qui démontre ne m’interpelle pas davantage.
C’est comme si on voulait juste gagner de l’encre.
Bien entendu, ce n’est pas que ça, je le sais.
La transitivité me semble aisé en 6e même s’il faut distinguer les cas dégénérés.
Sauf si quelque chose m’échappe. -
Si tu trouves que c'est aisé, même en 4ème avec toutes les caractérisations du parallélogramme, alors quelque chose t'échappe.
-
En 5e on a « si le quadrilatère a deux côtés opposés parallèles et de même longueur alors c’est un parallélogramme ».
En effet on n’a pas ça en 6e. En 6e on parvient facilement à montrer que deux côtés opposés sont parallèles mais pas simple pour les deux autres. -
La propriété que tu cites est fausse ...
-
Certes « convexes » ou « non croisés ».
-
Et c'est précisément là qu'est le problème ...
Comment justifier le "non-croisé" pour la "transitivité du parallélogramme", bien sûr en évitant "on voit bien que" (ce que j'appelais une escroquerie dans un message précédent) ? -
Oui, oui, je suis d’accord.
J’avais construit des choses avec des demi-droites jadis (ça revient à voir des vecteurs sans le dire, on parle ainsi des « sens »). ABCD parallélogramme dit notamment que [AB) et [CD) sont parallèles et de sens opposés.
ATTENTION : je ne dis pas qu’il faut s’interdire la caractérisation par les diagonales de même milieu, je parle d’une définition d’un objet appelé « parallélogramme ».
D’ailleurs même avec la définition que tu donnes, j’espère qu’on a bien un théorème qui dit « si côtés opposés parallèles, alors parallélogramme ». À moins de cacher ça sous le tapis (?).
On a un problème similaire pour les caractérisations avec les longueurs (« si côtés opposés de même longueur alors parallélogramme... »). Cas « non croisés » encore.
Dans ce fil d’ailleurs, une démonstration que j’ai tentée coince à cause d’une histoire de longueur (on trouve deux points possibles et il faut justifier que « c’est le bon qu’on obtient »). -
Ce n'est pas une histoire de définition (il faut évacuer les cas particuliers qui sont encore plus délicats à traiter), mais bien de comment démontrer proprement, sans "on voit bien que".
On est en train de dévier complètement du fil de départ. Je vais ouvrir un nouveau fil. -
Ok.
Ça me va bien comme ça cela dit. Je crois qu’on a un peu fait le tour.
En fait, dès que ça discute « lycée » il y a consensus il me semble.
Édit : ha ok je viens de voir le nouveau fil.
Tu as eu raison c’est plus général que « parallélogramme ».
Connectez-vous ou Inscrivez-vous pour répondre.
Bonjour!
Catégories
- 163.1K Toutes les catégories
- 8 Collège/Lycée
- 21.9K Algèbre
- 37.1K Analyse
- 6.2K Arithmétique
- 53 Catégories et structures
- 1K Combinatoire et Graphes
- 11 Sciences des données
- 5K Concours et Examens
- 11 CultureMath
- 47 Enseignement à distance
- 2.9K Fondements et Logique
- 10.3K Géométrie
- 62 Géométrie différentielle
- 1.1K Histoire des Mathématiques
- 68 Informatique théorique
- 3.8K LaTeX
- 39K Les-mathématiques
- 3.5K Livres, articles, revues, (...)
- 2.7K Logiciels pour les mathématiques
- 24 Mathématiques et finance
- 312 Mathématiques et Physique
- 4.9K Mathématiques et Société
- 3.3K Pédagogie, enseignement, orientation
- 10K Probabilités, théorie de la mesure
- 772 Shtam
- 4.2K Statistiques
- 3.7K Topologie
- 1.4K Vie du Forum et de ses membres




